眉山穆家溝水庫黏土心墻石渣壩應力應變及穩定性分析

廖 敏，李上策，彭愛華，王榮和，謝 意

(1.眉山市水利局， 四川 眉山 620010；2.簡陽市水務局， 四川 簡陽 641400)

近40年來，隨著土體本構模型的成熟應用和壩體碾壓施工技術的突破，土石壩的發展如雨后春筍，我國土石壩填筑已經由壩高200m級向300m級突破，例如已建成的糯扎渡(壩高261.5m)，正在建設的兩河口(壩高295m)、雙江口(壩高312m)[1]。心墻土石壩因就地取材方便、壩型結構簡單、施工技術成熟、對地質適應性強等綜合因素得到廣泛應用，研究心墻土石壩的應力應變具有重要工程意義。土石壩穩定性在設計中常用的是極限平衡法，但近年隨著有限元軟件的二次開發應用，有限元數值模擬日益應用到工程實際。

目前常用于心墻土石壩分析的本構模型有DuncanE-B模型、DuncanE-ν模型、清華K-G模型、南水模型及殷宗澤雙屈服面模型、Mohr-Coulomb模型等[2]，國內學者針對于土石壩開展了大量研究：歐陽君等[3]采用ABAQUS軟件對某土石壩進行應力與變形分析，認為鄧肯張模型二次開發可以有效的實現土石壩的應力、應變計算；李明梅[4]采用ABAQUS軟件分析了某心墻壩的滲流場與應力場對土石壩影響作用，認為DuncanE-B模型在土石壩中適用性較好；廖敏[5]采用ABAQUS軟件對某土石壩進行應力應變和穩定性計算，認為DuncanE-B模型和強度折減法對土石壩的計算是合理可行的；王曼等[6]采用強度折減法計算某邊坡，認為強度折減法計算結果可以為工程的設計施工提供參考依據。以上研究取得了較好的研究成果，體現出DuncanE-B模型和強度折減法在土石壩、邊坡中具有較好的適應性、實踐性、合理性，故本文基于以上研究，采用ABAQUS軟件二次開發對眉山穆家溝水庫心墻石渣壩進行應力應變計算和穩定性分析，為工程建設提供理論支撐。

1 DuncanE-B模型與強度折減法簡介

1.1 DuncanE-B模型

DuncanE-B模型[7]在E-ν模型基礎上進行了一定的完善，都采用相同的彈性模量，為了避免初始泊松比與實際泊松比的差別情況進行了改進，E-B模型的切線體模量Bt代替E-ν模型中的切線泊松比νt進行計算，表達式如下：

(1)

(2)

式中，σ3為最小主應力，pa為大氣壓強，Kb和m為常數，從而νt可以表示為：

(3)

1.2 強度折減法

強度折減法由Zienkiewicz提出，即給一折減系數Fr，對邊坡的所有土體單元進行強度折減，將土體抗剪強度參數不斷降低，折減后的參數不斷代入模型進行重復計算，直到邊坡達到極限發生破壞，此時的折減系數就是邊坡的安全系數，其公式[7]如(4)和(5)所示。

c'=c/Fr

(4)

φ'=arctan(tanφ/Fr)

(5)

式中的c和φ為土體折減前的抗剪強度指標；c'和φ'為土體折減后的抗剪強度指標；Fr是強度折減系數。

2 工程概況

穆家溝水庫工程位于眉山市東坡區，是一座具有農業灌溉、農村生活供水，以及改善眉山市岷東新區水生態環境等綜合利用的中型水利工程。穆家溝水庫工程壩址控制集水面積15.6km2，主河道河長8.10km，平均比降6.35‰。校核洪水位446.59m，設計洪水位446.27m，正常蓄水位445.50m，死水位435.00m，水庫總庫容1 408萬m3，正常蓄水位時相應庫容1 237萬m3，興利庫容1 029萬m3，死庫容208萬m3，總灌溉面積6.1萬畝，供水人口3.83萬人，工程多年平均供水量2 225萬m3。穆家溝水庫工程大壩為黏土心墻石渣壩，最大壩高35.0m，壩頂長575m，壩頂寬10.0m，大壩長575m，壩頂高程為448.00m。大壩上游設兩級坡，從上至下坡比分別為1∶2.5和1∶3.0，在高程438.00m處設2.5m寬的馬道；下游設兩級坡，從上至下坡比分別為1∶2.25、1∶2.5，在高程438.00m處設2m寬的馬道；高程428.00m以下為排水棱體，棱體內側坡比為1∶1，外側坡比為1∶1.8。下游壩殼高程424.00m-423.00m之間為1m厚的卵礫石反濾層，423.00m-420.00m之間為3m厚的卵礫石排水帶。本文選取壩體最大壩高橫截面(樁號0+200斷面)進行計算，大壩最大橫斷面簡圖如圖1所示。該心墻壩通過試驗取得部分工程試驗參數，未獲取鄧肯-張參數，本文結合勘察設計報告給的土體強度參數并通過類似的工程對比，具體計算參數取值如表1所示。

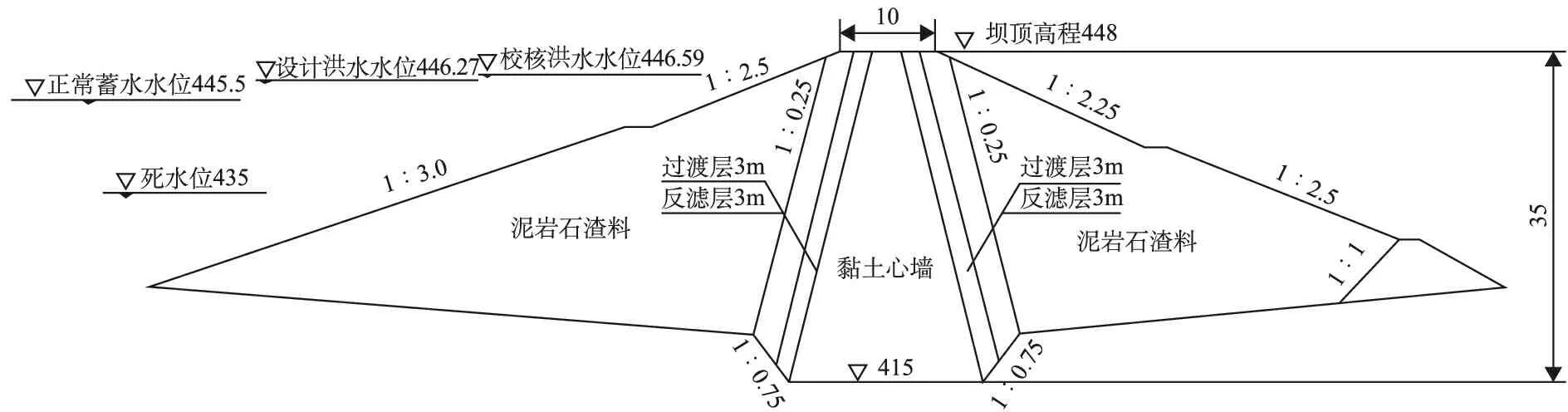
圖1 穆家溝水庫大壩最大橫斷面簡圖

表1 計算參數

表1中，K表示初始彈性模量的基數；n表示彈性模量參數；Rf表示破壞比，C表示黏聚力/kPa；φ為內摩擦角/0；Δφ為非線性內摩擦角增量；Kb為體積模量基數；Kur為卸載再加載時的彈模基數；m為體積模量指數；ρ為密度/(g/m3)。

3 應力應變分析

本次數值模擬采用分級填筑，生死單元模擬壩體變形，能較真實反映壩體的應力和變形情況。壩高35m，分7級填筑，每級5m，壩體填筑完后分正常蓄水位和校核洪水位施加靜水壓力，不考慮下游水深進行計算，計算的應力應變如表2所示。由表2可知，在靜水壓力作用下，蓄水后壩體的應力、位移較蓄水前大，壩體的應力應變符合一般心墻壩變形規律，表明本次模擬是合理的；壩體模擬的沉降位移比觀測數據大，是由于目前大壩剛填筑至壩頂不久，還在進一步沉降變形，故實際沉降量略低于理論計算。由于壩體正常蓄水位與校核洪水位相比應力應變差別不大，本文選取正常蓄水位時壩體應力應變進行分析。

表2 應力應變計算結果

3.1 應力分析

圖2和圖3位為壩體在蓄水期斷面主應力等值線變形云圖。由變形云圖可以知，最大主應力和最小主應力變化規律一致，壩體基本處于受壓狀態，最大主應力為0.626MPa，最小主應力為0.334MPa，均發生在壩體底部位置；壩體左右側應力等值曲線因為壩體左側施加靜水壓力的原因而不對稱，出現曲線上抬與上游壩坡相交；心墻、過渡層與石渣壩殼料材料力學性能不一樣，出現應力不連續并間斷的現象，導致應力曲線不光滑連續；壩頂及壩坡局部出現拉應力是因為模型的邊緣約束條件下產生了局部的拉應力。

3.2 位移分析

圖4為壩體蓄水期水平位移變形云圖，壩體上游水平位移為1.587cm，下游水平位移為4.342cm。壩體水平變形位置位于壩高1/2處，大致呈對稱狀分布；圖5為壩體蓄水期水平位移變形云圖，壩體的最大沉降量區域位于壩高1/2-2/3處，呈近似圓形向外擴展，壩體最大沉降為12.1cm，約占壩高的0.346%。壩體蓄水期相對于施工期變化不大，是由于模擬中采用生死單元、分級填筑，填筑中考慮了壩體的沉降，故蓄水后沉降較小。

圖2 蓄水期壩體最小主應力等值線云圖(單位：kPa)

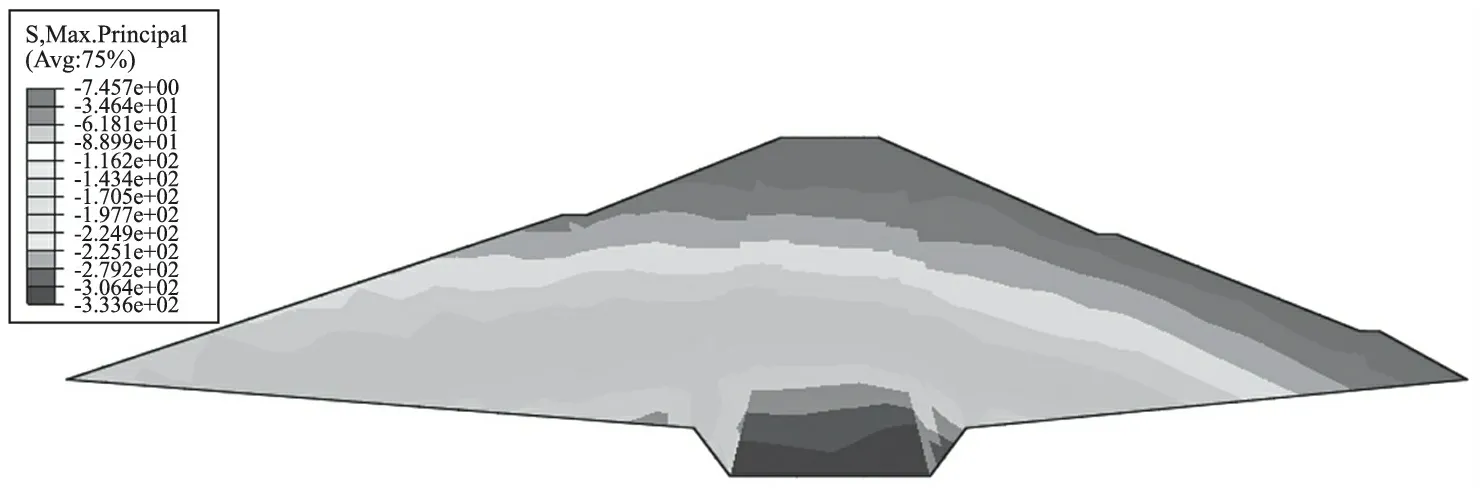
圖3 蓄水期壩體最大主應力等值線云圖(單位：kPa)

圖4 壩體蓄水期水平位移變形云圖(單位：m)

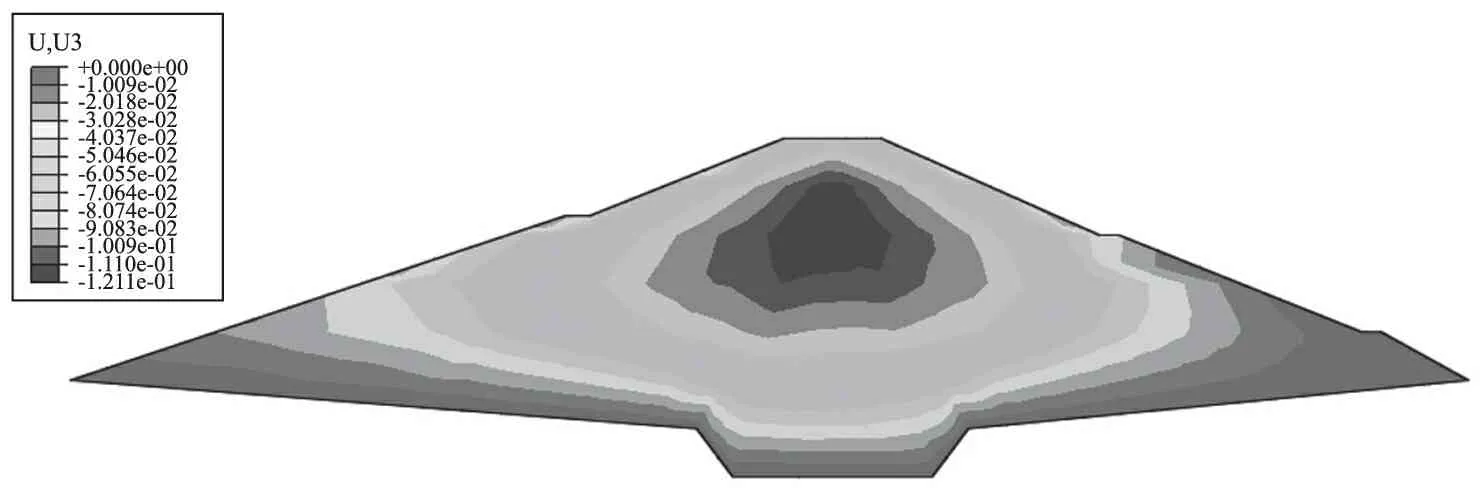
圖5 壩體蓄水期豎直位移變形云圖(單位：m)

4 穩定性分析

采用Mohr-Coulomb模型結合強度折減法對穆家溝水庫壩坡進行穩定性計算，直到迭代不收斂為止，采用特征位移突變結合塑性區貫通為判斷標準[8]，計算結果如表3所示。由表3可知，畢肖普法與強度折減法計算結果相近，均大于允許的安全系數，下游壩坡在三種工況下均是穩定的，表明本次模擬是合理可行的；上游壩坡總體安全系數較下游壩坡高，蓄水后上游壩體自重在水平上的分力抵消一部分靜水壓力，這與表2上游水平位移變化趨勢相符合；蓄水后相比于蓄水前安全系數下降幅度不大，緣于壩前蓄水位不高，兩種工況所產生的靜水壓力相近。

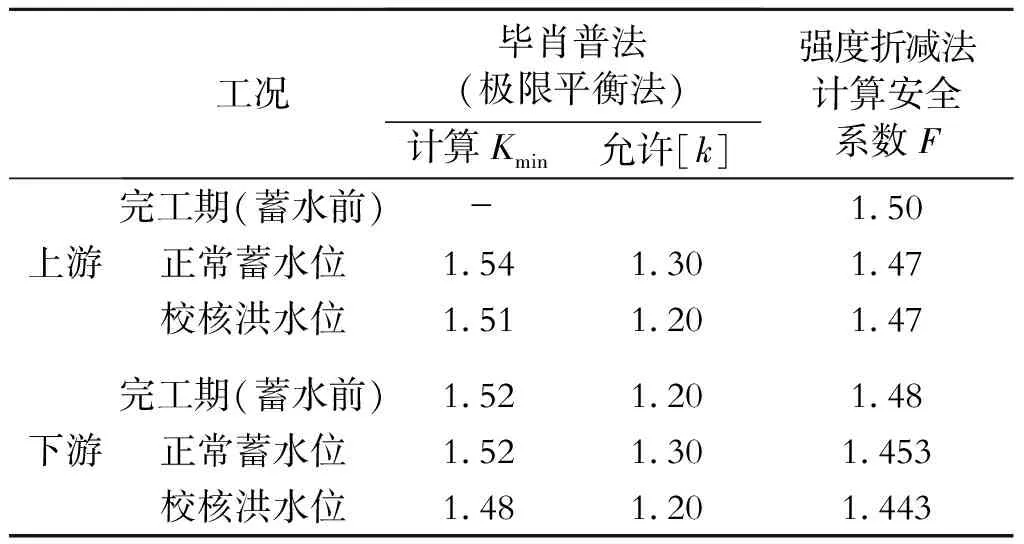
表3 強度折減法與畢肖普法安全系數計算結果比較

本文選取正常蓄水位工況下壩體塑性區域進行分析。圖6為蓄水期壩體塑性貫通區域，在靜水壓力作用下，從圖(a)到(b)下游壩坡從發生塑形變形到塑性貫通，塑形區域逐漸增大。塑性貫通區域發生在下游壩坡，一是下游壩坡坡比比上游陡，先出現滑動面，二是在靜水壓力作用下，塑性區域越來越明顯清晰。當折減系數為1.428時，壩體下游角處出現塑性區域，逐漸向壩體內側延伸，此時壩體是穩定的。當折減系數為1.453時，壩體塑形區域延伸至壩頂，發生塑性貫通(潛在即滑動面)，塑性貫通區域大致呈圓弧狀，符合黏土心墻石渣壩的變形特征，此時折減系數1.453即下游壩坡的安全系數。

圖6 蓄水期壩體塑性貫通區域

5 結 論

本文通過ABAQUS軟件二次開發DuncanE-B模型，結合Mohr-Coulomb模型對穆家溝水庫黏土心墻石渣壩進行應力應變和穩定性分析得出以下結論。

(1)采用DuncanE-B模型計算模擬的蓄水期壩體最大主應力為0.626MPa，最小主應力為0.334MPa，最大水平位移為4.342cm，壩體最大沉降為12.1cm。壩體應力應變符合一般土石壩變形規律，壩體位移與實際觀測相近，數值模擬是合理的，可以為理論和實際研究提供依據。

(2)采用Mohr-Coulomb模型結合強度折減法計算的壩坡安全系數與初步設計報告中畢肖普法結果相近，壩坡在正常蓄水期安全系數為1.453，校核洪水位安全系數為1.443，壩體蓄水后是穩定的，壩坡潛在滑動面符合黏土心墻土石壩變形特征。