多重接觸式靜密封泄漏特性定量分析模型

趙飛，張曉妹，劉鳴，王立權

（1.首都醫科大學附屬北京朝陽醫院 高壓氧科，北京 100020；2.黑龍江省城鎮住宅建筑工程有限公司，哈爾濱 150000；3.哈爾濱工程大學，哈爾濱 150001）

0 引言

接觸式靜密封是通過兩表面的相互接觸擠壓實現的，宏觀上看似平整的加工表面和自然表面均具有表面粗糙度，當兩表面相互接觸時，表面粗糙度使得實際接觸面積小于名義接觸面積，由于接觸區域存在微小孔隙，為密封介質的泄漏提供了可能。為了以較為經濟的方式獲得較好的密封性能，常采用多重接觸式靜密封，通過在泄漏方向上布置2個或2個以上密封區域，可以顯著提高整體的密封性能，因結構形式簡單，密封效果好，廣泛應用于海洋工程裝備、石油化工裝備、機械工程、建筑等領域。

近年來，國內學者提出了各種多重密封結構并開展了相關研究。韓飛[1]研究了浮頂儲罐雙密封結構，提出了在一二次密封空間填充密封物質的方法，抑制油氣聚集，降低安全隱患；宮乙帥等[2]研究了齒輪泵的雙密封結構，說明了雙密封可以顯著提高齒輪泵對外密封的可靠性；梁寧[3]分析了潛水潛污電動機電泵動的多重密封技術，說明了多重密封技術可以減少壓力梯度、降低泄漏量；張旭東等[4]提出了一種用于鉛蓄電池的雙重密封結構，通過實驗證實了雙密封結構具有顯著提高對電池內部酸液的密封性能，可有效提高電池的安全性和壽命；魏宗亮[5]提出了一種解決海底破損管道快速修復問題的水下連接器卡壓式水下連接器，該裝置采用雙密封結構，可有效提高油氣介質密封的可靠性。國內高校在接觸式靜密封泄漏特性定量分析方面開展了深入的理論研究工作。史建成等[6]提出了一種基于逾滲模型的接觸式靜密封泄漏量預測模型，分析了接觸面積、表面紋理方向對泄漏特性的影響；黃曉明等[7]基于MB模型和分形多孔介質理論，研究了金屬平墊片的泄漏特性；Hu等[8]將分形接觸模型用于氣體密封動態性能研究；Liu等[9]研究了水下連接器的密封特性，提出了流阻模型，給出了密封區域流阻、兩端壓力梯度和泄漏率的數學關系。

由以上分析可知，現有的研究工作對單密封的泄漏特性進行了深入研究，但對于多重接觸式靜密封的泄漏機理研究較少。本文提出一種多重接觸式靜密封理論模型，通過數值仿真分析了密封區域數量、密封區域間體積對泄漏特性的影響，為設計多重接觸式靜密封結構和定量分析其密封性能提供了參考。

1 理論模型

應用于不同領域、形式多樣的多重接觸式靜密封具有相似的結構和特點，提取關鍵特征，可簡化為一般性理論模型，包括密封腔體、腔體內壁、密封介質、密封區域、密封空間等，如圖1所示。密封圈與腔體內壁相互擠壓形成密封區域，由于表面粗糙度的存在，密封圈與腔體表面存在不完全接觸，形成泄漏通道。兩個相鄰密封區域可以形成一個密封空間。密封腔體內的液體密封介質具有較高壓力，在高壓驅動下通過密封區域和密封空間向低壓端泄漏，即密封腔體內液體密封介質在壓力差作用下，以一定的流量進行泄漏。

圖1 多重接觸式靜密封的一般性結構示意圖

多重接觸式靜密封的泄漏過程如圖2所示。在泄漏過程中，靠近高壓端的密封空間優先被液體充滿，且液體達到一定壓力后，才能繼續沿相鄰密封區域向下一密封空間泄漏，定義為密封區域的首次穩定泄漏狀態。密封介質沿壓力下降方向，經過數個密封區域和密封空間泄漏，最終向外界環境泄漏，定義為多重接觸式靜密封的首次穩定泄漏狀態。

圖2 多重接觸式靜密封的泄漏過程示意圖

為簡化問題，本文提出以下假設：1）將液體密封介質視為不可壓縮流體，忽略液體壓力對液體體積的影響，滿足流體連續性假設，密封介質流經密封區域的泄漏率相等。2）將液體密封介質泄漏過程視為理想狀態，忽略液體沿密封區域泄漏的非穩定泄漏情況，如密封空間內液體壓力累積過程、密封區域兩端壓力差不穩定情況、液體介質未完全貫通密封區域情況等。3）忽略密封空間內氣體壓力對液體密封介質泄漏的影響，將其等效為外界環境。

多重接觸式靜密封的密封空間數量為

多重接觸式靜密封第i個密封空間體積為Vci，可根據體積與泄漏率關系，得到第i個密封區域空間內充滿密封介質的時間，定義為第i個密封區域首次穩定泄漏時間：

密封介質流經多重接觸式靜密封最后一個密封區域的時間，定義為首次發生穩定泄漏的時間：

對于某些要求無泄漏的工況，如油氣管道、建筑防水等，一般以最后一道密封出現泄漏為密封失效。

2 數值仿真結果與討論

2.1 總流阻不同條件下的泄漏特性分析

考慮一系列多重接觸式靜密封，給定密封區域數量ns=1～8，壓力梯度為1 MPa，密封區域均采用相同流阻的密封單元，任一密封區域流阻Ri為5000、10 000、15 000 MPa·s/mL。

通過式（3）計算得到多重接觸式靜密封的密封區域數量與總流阻關系，如圖3所示。當密封區域流阻相同時，總流阻R與密封區域數量ns呈線性關系；當密封區域數量相同時，任一密封區域流阻Ri越大，總流阻越大。

圖3 密封區域數量與流阻關系

通過式（5）計算得到多重接觸式靜密封的密封區域數量與穩定狀態下泄漏率關系，如圖4所示。密封區域流阻相同時，隨密封區域數量ns增加，穩定狀態下泄漏率QL顯著降低，呈現非線性關系；當密封區域數量相同時，任一密封區域流阻Ri越大，泄漏率QL越小。

圖4 密封區域數量與泄漏率關系

給定任意密封空間體積為Vci=10.0 mL（10.0×10-6m3），分析不同密封區域流阻Ri對密封區域數量ns與首次穩定泄漏時間關系的影響。

由式（6）計算得到密封區域數量與第i個密封區域首次穩定泄漏時間ti的關系，如圖5所示。對于單密封結構（ns=1），忽略密封區域的不穩定泄漏時間，認為密封介質穩定泄漏時間為0。對于雙密封結構（ns=2），當其唯一一個密封空間被密封介質充滿時，認為其處于穩定泄漏狀態，以此類推，對于ns重密封結構，第i個密封空間充滿液體的時間ti，隨密封區域序號i增加而線性增大。由式（6）可知，密封區域數量ns不同的多重接觸式靜密封，第i個（i≤ns，ns>1）密封區域首次穩定泄漏時間ti相同，其與已發生穩定泄漏的密封區域情況相關，與密封區域總數ns無關，出現圖5所示的數值曲線重合情況。

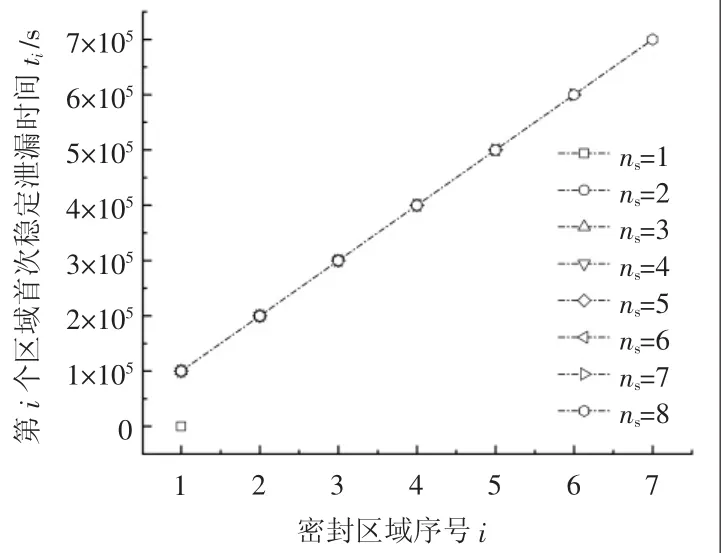
圖5 密封區域數量對第i個密封區域首次穩定泄漏時間的影響

由 式（7）可得，密封區域流阻對首次發生穩定泄漏時間的影響，如圖6所示。隨密封區域數量ns增加，首次穩定泄漏時間T 非線性增大；當密封區域數量ns相同時，密封區域流阻Ri越大，首次穩定泄漏時間T越大。這是由于流阻降低了泄漏率，液體密封介質需要更長時間才能充滿密封空間。

圖6 密封區域流阻對首次發生穩定泄漏時間的影響

由圖7可知，當多重靜密封結構處于穩定泄漏狀態時，密封區域數量ns越大，任一密封區域承擔的壓力差Δpi越小；密封區域流阻Ri對壓力差Δpi無影響。

圖7 密封區域數量對壓力差分擔作用的影響

2.2 總流阻相同條件下的泄漏特性分析

為進一步分析多重接觸式靜密封的泄漏特性，在總流阻相同情況下，調整密封區域數量和密封空間體積。給定密封區域數量ns=1～8，壓力 差 為 1 MPa，總流阻R =10000 MPa ·s/mL，密封區域均采用相同流阻的密封單元，任一密封區域流阻為Ri=R/ns，密封空間體積Vci為10.0、15.0、20.0 mL。

由圖8可知，當Vci=10.0 mL時，多重接觸式靜密封第i個密封空間充滿液體的時間ti，隨密封空間序號i增加而線性增大；當密封空間序號i相同時，密封區域數ns越大，第i個密封空間充滿液體的時間ti越小，這是因為參與穩定泄漏的密封區域流阻總數較小，而壓力差不變。

圖8 密封區域數量對第i個密封區域首次穩定泄漏時間的影響

由圖9可知，多重接觸式靜密封的密封區域數量ns越大，首次穩定泄漏時間T越大；當密封區域數量ns相同時，密封空間體積Vci越大，首次穩定泄漏時間T越大，這是因為在泄漏率相同的情況下，液體密封介質需要更多時間充滿密封空間。

由以上分析可知，總流阻相同的多重接觸式靜密封，密封區域數量ns越大，密封空間體積Vci越大，發生穩定泄漏的時間T越大，密封性能越好。

3 結論

本文分析了多重接觸式靜密封的主要特征，建立了理論模型，通過數值仿真分析了密封區域數量、密封空間體積對泄漏特性的影響，主要得到了以下結論：1）通過增加多重接觸式密封結構的密封區域數量，提高總流阻，有利于提高密封性能，獲得更低的泄漏率。2）通過增加多重接觸式密封結構的密封空間體積，可延長形成穩定泄漏時間，尤其適用于針對一些工況較為惡劣、工作時間較短的密封工況，在很難提高密封等級的情況下，增大密封空間體積，是一種較為經濟的方法。3）在總流阻相同的情況下，可通過增加密封區域數量和密封空間體積，顯著提高密封性能，尤其是適用于要求較高的密封條件。

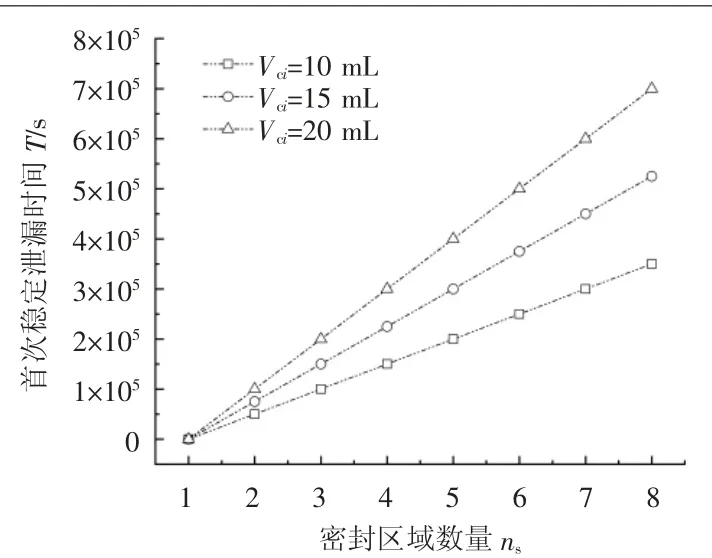
圖9 密封空間體積對首次穩定泄漏時間的影響

該理論模型也同樣適用于動密封和非接觸式密封，在確定密封流阻的情況下，可以對多重密封進行結構設計，為密封性的定量分析提供了參考。