圓錐曲線中“三定兩動一軌跡”問題

余桃

【摘要】圓錐曲線的軌跡問題是高考數學試題的常見問題之一，但圓錐曲線的內容對于大部分學生來說是學習的難點.筆者整理分析發現歷年高考數學試題中均能在教材中找到相應例題或習題的縮影.通過對此類問題的歸納總結，可以有效提升學生的學習效率.

【關鍵詞】圓錐曲線；定值；軌跡

1.習題展現

題目△ABC的兩個頂點A，B的坐標分別為（-6，0），（6，0），邊AC，BC所在直線的斜率之積等于-49.求頂點C的軌跡方程.（北師大版選修2-1）

這里可以設頂點C的坐標為（x，y），進而表示出邊AC，BC所在直線的斜率

kAC=yx+6和kBC=yx-6.

根據題意可知kAC·kBC=-49，

即yx+6·yx-6=-49，

整理得x236+y216=1.

當y=0，點C和點A（或點B）重合，不符合題意.故所求點C的軌跡方程為x236+y216=1（y≠0）.

根據上述解析過程可知，如果邊AC，BC所在直線的斜率之積等于-49，則頂點C的軌跡是一個橢圓（除去頂點A，B）.

2.習題推廣

現將此題做一般化處理，即設兩個頂點A，B的坐標分別為（-a，0），（a，0），若兩條直線AC，BC相交于點C，且它們的斜率之積等于定值m（m≠0），那么交點C的軌跡是什么？接下來我們進行嚴格的證明：

證明設交點C的坐標為（x，y），

當x≠±a時，根據題意得

kAC·kBC=yx+a·yx-a=m（m≠0），

即mx2-y2=ma2（x≠±a）.

因為當x≠±a時，點C和點A（或點B）重合，不符合題意，

故點C的軌跡方程為

x2a2-y2ma2=1（x≠±a）.

當m>0時，點C的軌跡是焦點在x軸上的雙曲線（除去A，B）；

當-1<m<0時，點C的軌跡是焦點在x軸上的橢圓（除去A，B）；

當m=-1時，點C的軌跡是以原點為圓心、以|a|為半徑的圓（除去A，B）；

當m<-1時，點C的軌跡是焦點在y軸上的橢圓（除去A，B）.

m取不同值時點C的軌跡

m的取值范圍交點C的軌跡圓錐曲線類型m>0雙曲線-1<m<0橢圓m=-1圓m<-1橢圓

有趣的是，如圖1所示，在該曲線上任取一點G，將點G繞原點O旋轉180°得到點G′，即點G，G′是該曲線上關于原點對稱的兩點.圖1然后在該曲線上另取一個異于G，G′的點H，分別連接HG和HG′，計算發現kHG·kHG′=m，如果改變m的值，上述結論保持不變.這里，我們可以得到一個結論：

性質1設G，G′是圓錐曲線mx2-y2=ma2（x≠±a）上關于原點對稱的兩點，點H是該曲線上不同于G，G′的任一點，則kHG·kHG′為定值m.

證明設H（x0，y0），G（x1，y1），

因為點G和G′是該曲線上關于原點對稱的兩點，

所以G′（-x1，-y1）.

又因為點H，G′在曲線mx2-y2=ma2（x≠±a）上，

所以mx20-y20=ma2，mx21-y21=ma2，

由此可得m（x20-x21）=y20-y21，

即y20-y21x20-x21=m，

而kHG=y0-y1x0-x1，kHG′=y0-（-y1）x0-（-x1）=y0+y1x0+x1，

所以kHG·kHG′=y0-y1x0-x1·y0+y1x0+x1=y20-y21x20-x21=m.

接下來，我們對斜率之積為定值問題做進一步探究：

圖2

當kAC·kBC=m，m∈（-1，0）時，過原點O作OM∥AC，ON∥BC，與橢圓分別交于點M，M′，N，N′，連接ON，NM，MO，得到△OMN（如圖2），直線AC繞著點A轉動，可以發現△OMN的面積始終保持不變.進一步研究可發現，該定值是-m·a22，并且當kAC·kBC=m，m∈（-∞，0）時，此結論恒成立，因此我們可以得到一個結論：

性質2若橢圓方程為x2a2+y2b2=（a>b>0），過原點的兩條直線l1和l2分圖2別交橢圓于點M，M′和N，N′，則直線l1和l2的斜率之積為-b2a2，這是S△OMN=12ab的充要條件.

證明在仿射變換x′=xa和y′=yb下，橢圓變為圓x′2+y′2=1.

（1）充分性.

由x2a2-y2ma2=1（-1<m<0），x2a2+y2b2=1（a>b>0），

可知kl1·kl2=m=-b2a2=e2-1，-m·a=b，

所以仿射變換后直線l′1和l′2的斜率之積等于-1，

因此△O′M′N′是邊長為1的等腰直角三角形，

故S△OMN=abS△O′M′N′=-m·a22=12ab.

（2）必要性.

當S△OMN=12ab時，進行仿射變換后，△O′M′N′在圓x′2+y′2=1中是邊長為1的等腰直角三角形.

由kM′O′·kN′O′=-1，知kl1·kl2=-b2a2.

上述結論當該曲線變化為焦點在y軸上的橢圓或者圓時，結論仍然成立.

3習題的再推廣

更一般地，如果直線AC，BC的斜率之和（或差或商）等于定值m時，交點C的軌跡是什么？接下來，我們探究當kAC和kBC的和、差、商也為定值m（m≠0）時交點C的軌跡.

當kAC+kBC=m（m≠0）時，

設點C（x，y），x≠±a，

根據題意有

kAC+kBC=yx+a+yx-a=m（m≠0），

即mx2-2yx-ma2=0（x≠±a），

故所求點C的軌跡方程為

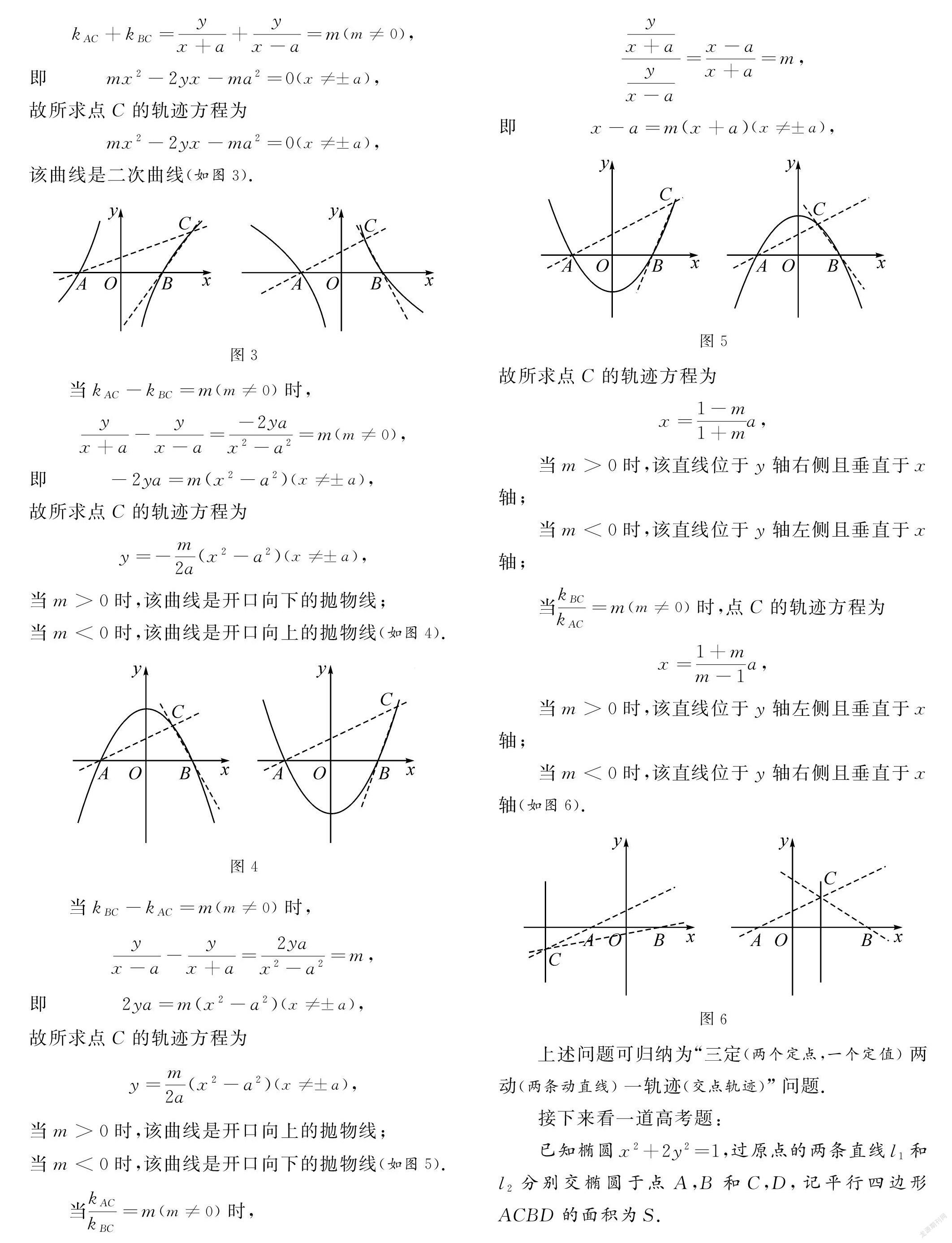
mx2-2yx-ma2=0（x≠±a），

該曲線是二次曲線（如圖3）.

圖3

當kAC-kBC=m（m≠0）時，

yx+a-yx-a=-2yax2-a2=m（m≠0），

即-2ya=m（x2-a2）（x≠±a），

故所求點C的軌跡方程為

y=-m2a（x2-a2）（x≠±a），

當m>0時，該曲線是開口向下的拋物線；

當m<0時，該曲線是開口向上的拋物線（如圖4）.

圖4

當kBC-kAC=m（m≠0）時，

yx-a-yx+a=2yax2-a2=m，

即2ya=m（x2-a2）（x≠±a），

故所求點C的軌跡方程為

y=m2a（x2-a2）（x≠±a），

當m>0時，該曲線是開口向上的拋物線；

當m<0時，該曲線是開口向下的拋物線（如圖5）.

當kACkBC=m（m≠0）時，

yx+ayx-a=x-ax+a=m，

即x-a=m（x+a）（x≠±a），

圖5

故所求點C的軌跡方程為

x=1-m1+ma，

當m>0時，該直線位于y軸右側且垂直于x軸；

當m<0時，該直線位于y軸左側且垂直于x軸；

當kBCkAC=m（m≠0）時，點C的軌跡方程為

x=1+mm-1a，

當m>0時，該直線位于y軸左側且垂直于x軸；

當m<0時，該直線位于y軸右側且垂直于x軸（如圖6）.

圖6

上述問題可歸納為“三定（兩個定點，一個定值）兩動（兩條動直線）一軌跡（交點軌跡）”問題.

接下來看一道高考題：

已知橢圓x2+2y2=1，過原點的兩條直線l1和l2分別交橢圓于點A，B和C，D，記平行四邊形ACBD的面積為S.

（1）設A（x1，y1），B（x2，y2），用A，C的坐標表示點C到直線l1的距離，并證明

S=2|x1y2-x2y1|；

（2）設l1與l2的斜率之積為-12，求面積S的值.

解（1）由題意知，A，C兩點的橫坐標不能同時等于零，

當A，C兩點的橫坐標有一個等于零時，不防設x1=0，x2≠0，不失一般性，此時直線l1與y軸重合，點C到直線l1的距離為|x2|，平行四邊形ACBD的面積為S=2|x2y1|；

當A，C兩點的橫坐標均不等于零時，即直線l1和l2的斜率均存在時，

設直線l1的方程為y=kx，其中k=y1x1，

由y=kx，x2+2y2=1，得（2k2+1）x2-1=0，

所以x1+x2=0，x1·x2=-12k2+1.

故|AB|=|x1-x2|

=1+k2·（x1+x2）2-4x1x2

=21+k22k2+1=2x21+y212y21+x21

=2x21+y21，

點C到直線l1的距離為

d=|kx2-y2|1+k2=|y1x2-y2x1|x21+y21，

所以平行四邊形ACBD的面積為

S=|AB|·d=2|x1y2-x2y1|.

綜上知，點C到直線l1的距離為

|y1x2-y2x1|x21+y21，

平行四邊形ACBD的面積為

2|x1y2-x2y1|.

（2）解法1由直線l1和l2的斜率之積為

-b2a2=-12，

知平行四邊形的面積為

S=4S△AOC=2ab=2.

解法2易知兩條直線的斜率分別為

kl1=y1x1，kl2=y2x2，

由直線l1和直線l2的斜率之積為-12，

得x1x2=-2y1y2，

又因為x21=1-2y21，x22=1-2y22，

所以x21x22=（-2y1y2）2

=1-2（y21+y22）+4y21y22，

即y21+y22=12，

S2=（2|x1y2-x2y1|）2

=4（x21y22+x22y21-2x1y1x2y2）

=4［y22（1-2y21）+y21（1-2y22）+4y21y22］，

化簡得S2=4（y21+y22）=2，

所以平行四邊形的面積為2.

解法3設直線l1的斜率為k，

則直線l2的斜率等于-12k.

設直線l1的方程為y=kx，

聯立方程組y=kx，x2+2y2=1，

消去y，得x=±11+2k2，

根據對稱性，設x1=11+2k2，

則y1=k1+2k2，

同理x2=2k1+2k2，y2=-221+2k2，

所以S=2|x1y2-x2y1|=2.

圓錐曲線的“三定兩動一軌跡”問題，可以考查學生數學運算、邏輯推理和直觀想象的數學核心素養.掌握該類問題有助于提升學生具有較強的綜合能力和應變能力.