面向錯位裝配體的自動曲面嵌入算法

劉智偉，楊 洋，陳建軍，*，鄭 澎，夏一帆

(1. 浙江大學 航空航天學院，杭州 310027；2. 中國工程物理研究院 高性能數值模擬軟件中心，北京 100088)

0 引 言

數值模擬前，用戶通常先定義CAD 模型，然后生成計算網格，最后設置邊界條件、材料和求解參數，這一過程被統稱為前處理[1]。實際應用中，前處理過程用戶交互頻繁，易錯且耗時長，是數值模擬的主要瓶頸[2]，研究前處理自動化算法是解決這一瓶頸的關鍵，亟待解決的難題包括網格自動生成、模型自動修復和清理等[3-5]。

本文研究由多個部件“組裝”而成的裝配體模型的自動修復算法。隨著軟硬件性能的不斷提高，以裝配體模型為輸入的多部件耦合數值模擬已成為發展趨勢。相比傳統的單部件模擬，這類模擬可以系統性和綜合性地考慮不同部件之間的幾何物理耦合關系，實現更高精度的數值模擬結果。當裝配體模型具有成百上千、乃至更多數目部件時，為降低建模難度，普遍采用分部件建模的方式，導致部件和部件之間的共享區域在不同部件中存在多份幾何表征。調用網格生成算法后，共享區域的網格也相應存在多份幾何和拓撲上都不兼容的表征，無法在共享區域生成保形的網格，也即不能作為常規數值模擬的輸入。

為此，本文提出利用“曲面嵌入”技術消除裝配體不同部件交疊部分存在的多重定義。以圖1 所示兩部件裝配體為例，若直接在該模型的原始邊界表征（如圖1（a））上生成網格，曲面1 和曲面2 的網格不兼容，不符合數值模擬的需要；執行曲面嵌入操作后（如圖1（b）），曲面2 一分為二，部件2 （Volume2）和部件1 （Volume1）重疊部分直接引用曲面1，其余部分定義為新曲面2（含圓形孔洞的長方形）。顯然，曲面嵌入消除了原曲面1 和曲面2 重疊區域的多重定義，在執行嵌入操作后獲得的模型上可生成符合常規數值模擬輸入要求的計算網格。

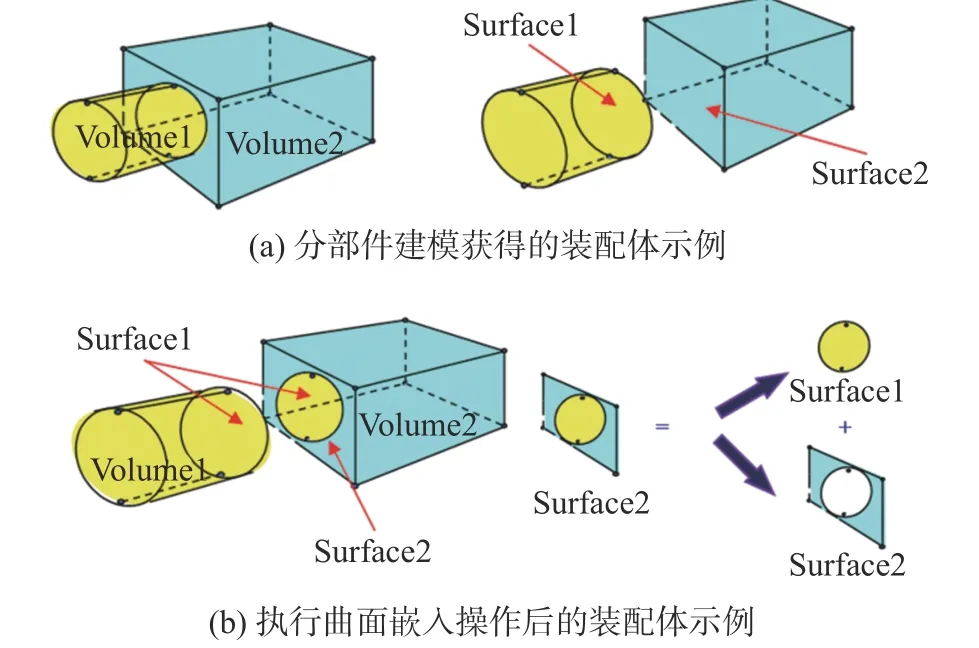
圖1 曲面嵌入操作示意Fig. 1 Illustration for surface imprinting operation

已有曲面嵌入算法分兩類：一類基于連續曲面，另一類基于離散曲面。連續曲面類算法其結果幾何精度高，但幾何計算復雜，數值穩定性差[6-8]。離散曲面類算法幾何計算為線性計算，運算速度快，但其結果幾何精度較低[9-14]。此外，離散曲面表征只涉及面片相鄰等低層拓撲，應用于需高層拓撲支持的操作時，需構造連續曲面模型中常用的邊界表征（B-rep）[15]。其中，第一類算法的代表有CADfix[16]，其通過人工交互方式在連續B-rep 直接進行相關的嵌入操作；第二類算法比較典型的如libigl[17]，其提供在離散三角形網格上處理三角形相交的算法，此外，TetWild[18]提供一種通過四面體優化的方法來完成模型嵌入及修復的方法，其本質依然是一種基于離散面片的方法。

在前期研究中，陳建軍等[3-4]提出一類將曲面連續表征和離散表征有機融為一體的曲面表征新方法，定義其為曲面的混合表征。本文針對錯位裝配體中幾何重復表征問題，提出基于連續-離散混合曲面造型的裝配體模型自動曲面嵌入算法。與前期研究工作[3-4]不同的是，該算法不僅消除曲面間曲線交纏等錯誤，更進一步消除模型實體間的曲面重疊、相交、錯位等錯誤。

1 算法流程

圖2 給出了本文所提面向錯位裝配體自動曲面嵌入算法的流程，該算法輸入錯位的裝配體幾何模型，輸出曲面嵌入后可用于生成計算網格的B-rep 幾何。

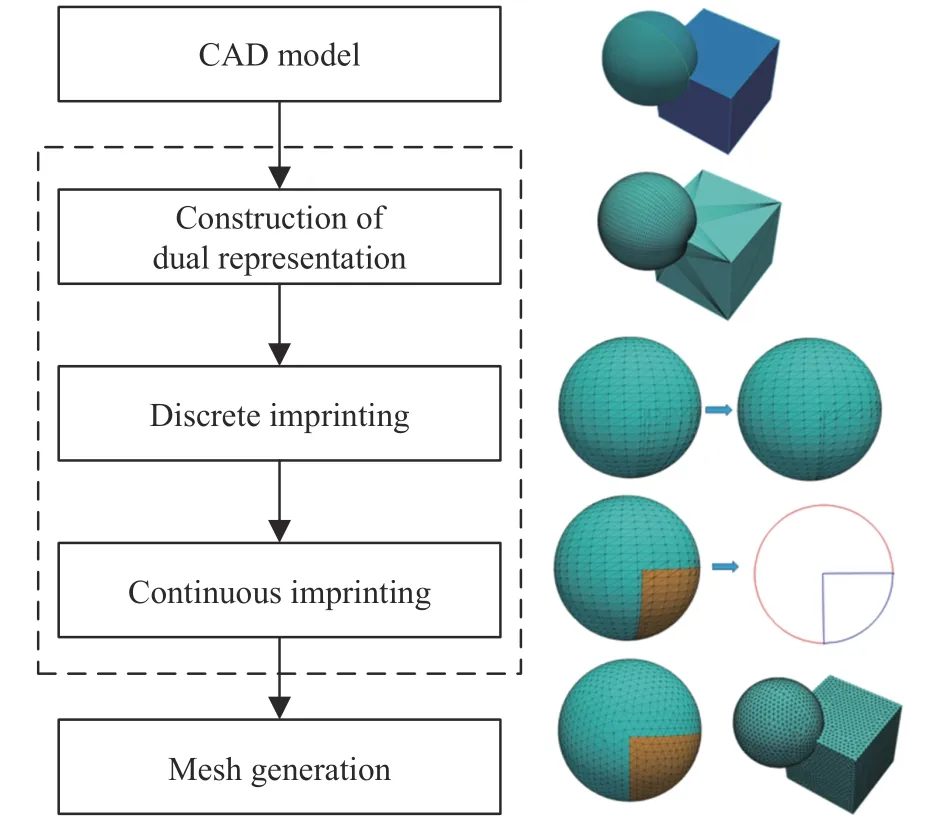
圖2 算法流程圖Fig. 2 The workflow of the algorithm

本文所提算法主要包含如下步驟：

1）構建混合曲面表征。建立裝配體模型的離散-連續表征數據結構，利用B-rep 表征連續曲面模型，采用輻射邊表征離散曲面模型，同時維護連續模型和離散模型兩者之間的映射關系。

2）離散曲面嵌入。通過檢測并計算離散模型上的共享邊界區域相交，將邊界線段嵌入相關的離散曲面中，進而在離散層面上計算出離散邊界相交環圖；而后通過拓撲操作移除其他區域的相交，完成在離散曲面嵌入。同時，在嵌入的過程中，同步更新離散-連續曲面表征的映射關系。

3）連續曲面嵌入。根據邊界相交圖、離散模型嵌入結果及維護的連續-離散映射關系，在自主的幾何引擎中設計相應的嵌入、合并操作，自底向上依次完成曲線嵌入、曲面嵌入，生成共享區域表征一致的B-rep。

執行曲面嵌入算法后輸出的裝配體模型B-rep 其不同部件邊界曲面交疊部分不再存在多重定義問題，以其為輸入，順序執行單元尺寸計算[19-20]、曲面網格生成[21]和實體網格生成[22-23]等算法，即可最終獲得符合通用數值模擬分析的計算網格模型。

2 算法實現

本文算法在連續-離散混合曲面表征上進行曲面嵌入操作，需首先建立模型的混合曲面表征：給定CAD模型輸入，將CAD 模型逐條曲線、逐張曲面離散，繼而根據離散模型和CAD 模型的對偶關系建立初始的混合曲面表征[3]。

模型的連續-離散混合表征建立后，繼而需解決離散模型的幾何相交問題及求得邊界相交圖，同時更新連續曲面模型的B-rep。下文2.1 節和2.2 節分別介紹上述兩個步驟的實現。為方便理解，文中引用圖3 所示的典型錯位裝配體展現本文算法各個過程中的處理效果，圖3 為模型的離散化形式，在曲面0 和曲面7 處發生重疊導致相交。

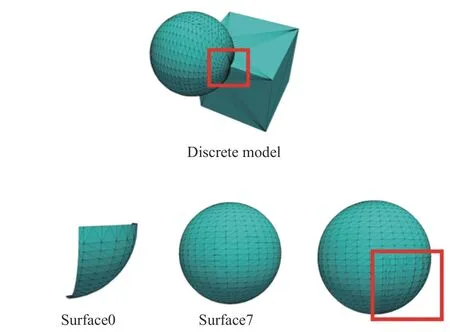
圖3 典型的錯位裝配體Fig. 3 Typical misaligned assembly

本文中，離散模型中端點為B-rep 中幾何頂點離散對應的網格點，邊界線段指代由B-rep 中的曲線離散而成的網格邊，而三條網格邊中一條或者多條為邊界線段的三角形被稱為邊界三角形。

2.1 離散曲面嵌入

離散曲面嵌入的目標有兩個：一是計算邊界相交圖；二是移除三角形相交。

2.1.1 計算邊界相交圖

邊界相交圖為一個曲面的邊界（曲線）與其重疊的曲面求交形成的新的邊界環圖。如圖4（a）所示，曲面A 和B 重疊于共享區域C，其邊界相交圖為圖4（b），求交得到的交點及曲線形成新區域C 的邊界。

圖4 邊界相交圖示意Fig. 4 Intersected graph of boundary

本文嵌入算法通過求解邊界線段-三角形處相交以求得離散層面上的邊界相交圖，計算過程主要包括三個步驟：1）檢測三角形相交；2）嵌入邊界線段；3）邊界線段一致化處理。

以圖4 中所示情形為例，詳細介紹離散邊界相交的計算，圖5（a）為該情形的離散表征。

1）檢測相交三角形相交。本文模型中的單個部件間不存在自相交問題，所有的三角形相交都存在于部件與部件的相鄰處，所以本文通過計算部件相鄰區域處的三角形距離來檢測三角形相交。距離計算分為兩類：第一類通過精確的三角形相交檢測得到距離為零的三角形集合及其對應的曲面索引對；第二類針對相鄰部件間在相鄰曲面處存在細縫的情況，通過對部件、曲面、對應的面片集合層層進行誤差 ε范圍內的包圍盒相交測試，不斷縮小范圍至可能相交的三角面片，最后通過精確的解析計算三角形間的距離，若兩個三角形間的距離小于設定誤差ε，則認為三角形相交。其中，誤差 ε的設置與模型相關，本文建議選取模型最小特征長度的1/10。如圖5（b）所示，紅色線段所圍成的三角形即為相交的三角形，根據離散-連續映射關系可得知曲面A和B為相交索引對。

2）嵌入邊界線段。根據相交檢測得到相交曲面索引對，提取各自曲面的邊界三角形上相交邊界線段（圖5（b）中紅色較粗線段），將曲面B的邊界線段通過線段-三角形求交嵌入進曲面A，同樣，將曲面A中的邊界線段嵌入進曲面B，結果分別如圖5（c）和5（d）所示。

3）邊界線段一致化處理。在相交曲面索引對中邊界線段的嵌入過程中，因嵌入過程各自獨立，此過程中可能產生圖5（c）和5（d）中邊界線段不一致的情形，因此在嵌入過程中需要追蹤原始邊界線段的分裂狀態，在對應的邊界線段上插入點使得相交曲面各自的邊界線段一致，如圖5（e）所示，通過插入點（空心點）得到一致的邊界線段。

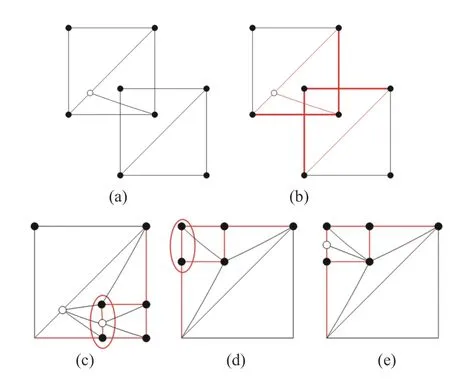
圖5 離散邊界相交圖計算Fig. 5 Computational process of intersection graph

步驟2 中線段-三角形相交計算中具體的相交形式可分類為5 種：點點相交、點邊相交、點面相交、邊邊相交、邊面相交。除點點相交外，其余4 類相交均存在退化情形，如點是邊的端點、點是面片的端點、兩條邊相交于其中一條邊的端點、邊和面片相交于邊或面片的端點等。但是，若按照上文所列順序依次處理上述相交情形時，相應退化情形會預先得到處理。例如，點邊相交的退化情形（點是邊的端點）在點點相交時已處理完畢，因此，檢測和解除點邊相交時只需考慮點對邊的投影位于邊的中間這一非退化情形。同理，邊面相交中，邊和面片相交于邊或面片的端點，這一退化情形會在點點相交、點邊相交或點面相交對應的操作中得到處理；邊和面片相交于面片的邊界線段這一退化情形，會在邊邊相交對應的操作中得到處理。因此，在實現相交的檢測和解除算法時，只要按順序處理，就無需考慮退化情形，相應算法的實現得到大幅度簡化。這里需要注意的是，處理相交的全過程中，我們需要及時更新和維護對應的混合曲面表征。基于上述思路，表1 的算法1 給出了處理所列5 種相交以獲得正確的邊界離散曲面拓撲的算法流程。注意，因本文所考慮的輸入不存在邊界上邊面相交情形，算法1 并未包含邊面相交情形的處理。另外，同一個點可能與多個點、邊、面相交，邊和面也類似。

表1 算法1 線段-三角形相交Table 1 Algorithm 1 segment-triangle intersections

2.1.2 移除三角形相交

求得離散邊界相交圖后，在相交曲面的重疊區域形成了一致的邊界線段（圖5（c、e）），然而在共享區域內部，三角形-三角形相交依然存在。本文在維護好的離散-連續映射關系的輔助下，通過拓撲關系移除共享區域的三角形相交。該拓撲方法避免了實際的三角形-三角形求交計算，也不存在浮點誤差范圍內面片求交的健壯性問題。移除共享區域的三角形相交在離散層面形成一致的幾何表征，不僅可有效輔助后續的連續曲面上的嵌入及合并操作，而且可以將該離散表征直接作為文獻[19]中定義尺寸函數的背景網格，與連續B-rep 一起作為網格生成的兩個完整的輸入。

本文通過拓撲方式移除三角形-三角形相交主要分為兩步：

1）遍歷所有曲面，對單個曲面的三角面片根據邊界線段進行“染色”，并根據染色結果進行區域劃分。圖6（a）和圖6（b）分別展示了對圖5（c）和圖5（e）中三角面片進行區域劃分的結果。

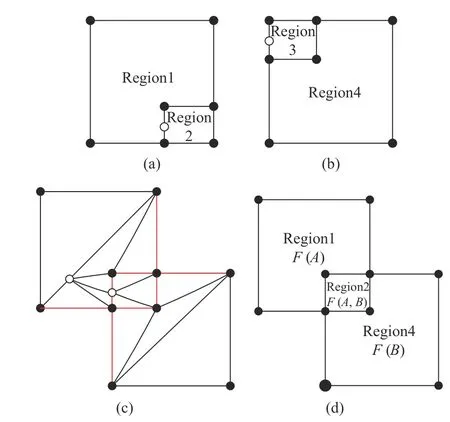
圖6 移除三角形相交Fig. 6 Removal of triangle-triangle intersections

2）對相交曲面對中的區域進行拓撲比對，若兩個區域擁有相同的邊界線段，則該區域視為重疊區域，然后刪掉一個區域內的一個三角面片，移除三角形相交，同時更新離散-連續映射關系。如圖6 所示，通過拓撲對比可得知，區域2 與區域3 有著相同的邊界線段，因此這兩個區域為共享區域，圖6（c）中刪掉了區域3 中三角面片，移除了重疊區域的三角形相交。圖6（d）為更新后的連續曲面表征示意，區域2 處為原始曲面A和B的重疊區域，因此該區域三角面片對應的連續曲面索引為A、B。

圖7 展示了圖3 例子經邊界相交圖計算和三角形相交移除后，在曲面0 和曲面7 相交區域的離散結果。圖7（b）為嵌入后的結果，該區域三角形相交已被正確移除，曲面0 中的邊界線段也已成功嵌入新的曲面中。

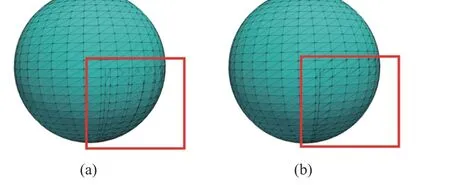
圖7 離散曲面嵌入結果Fig. 7 Results of discrete imprinting

2.2 連續曲面嵌入

本文算法意在獲取一個完成曲面嵌入的連續B-rep，以支持后續的網格生成算法。離散曲面嵌入完成后，還需在連續B-rep 上完成相應的自動曲面嵌入。

連續B-rep 的曲面嵌入主要涉及兩種基本操作：分裂與合并。其中分裂又分為曲線分裂和曲面分裂；合并分為頂點合并、曲線合并及曲面合并。根據離散曲面嵌入過程中得到的邊界相交圖及在重疊區域獲得的一致的離散表征，在離散-連續映射關系的輔助下，本文設計了相應的分裂及合并操作，自底向上完成連續B-rep 的自動曲面嵌入。本文中的連續幾何采用文獻[1]中具有完全自主知識產權的簡化的幾何引擎所提供的B-rep 表征，其核心為基于Ferguson曲線和Conns 曲面的裁剪曲面。本文所設計的分裂與合并操作均為拓撲操作，完全保留曲線/曲面的嚴格數學表達，故而能夠最大程度地保留嵌入過程中的幾何精度，也為后續的網格生成提供了精度保證。

2.2.1 分裂操作

曲線分裂：對于一條曲線，遍歷其對應的邊界線段，若其對應的邊界線段中包含多于2 個端點，則根據這些端點對該曲線進行分裂。如圖8（a）所示，曲線1 對應的邊界線段中包含有3 個端點（黑色實心點），因此根據邊界線段中間的端點對曲線1 進行分裂，得到圖8（b）中新的曲線1 和曲線2，并同時更新離散-連續映射關系。

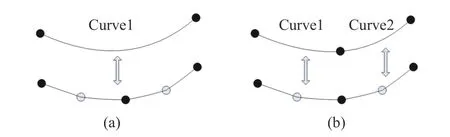
圖8 曲線分裂過程Fig. 8 Splitting of a curve

曲面分裂：對于一個曲面，首先對其所對應的三角面片根據其屬性（曲面索引）進行分類，若該曲面包含多個種類的三角面片，則根據面片分類結果對該曲面進行分裂。分裂過程中，曲面的支撐曲面保持不變，根據分類的三角面片中包含的邊界線段所對應的曲線屬性形成新的環，完成曲面的分裂。圖9 為圖3例子在重疊區域的曲面分裂過程，原始曲面7 中包含有兩種屬性的三角面片，分別為屬性7 和屬性0、7，根據不同種類三角面片上邊界線段對應的曲線索引，保持支撐曲面不變的情況下形成新的環，分裂為新的曲面7 和曲面8，其B-rep 如圖9（b）所示，并同時更新離散-連續映射關系。

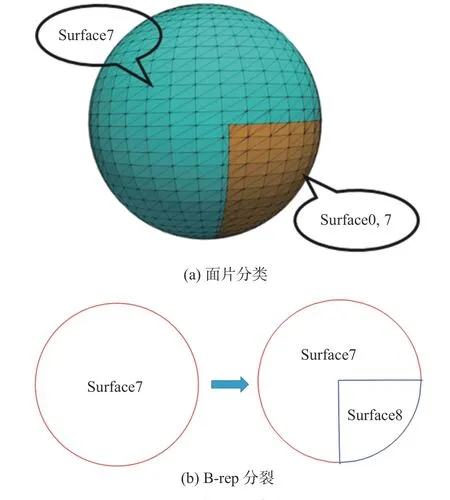
圖9 曲面分裂過程Fig. 9 Splitting of a surface

此外，在曲面分裂的過程中可能出現截斷的多區域情形，如圖10，曲面A和曲面B重疊于曲面AB區域（橙色），在三角面片分類過程中，曲面A中的面片將被分為三部分，共享區域AB和互不連通的兩個A區域。鑒于此種情形，本文算法對每一類三角面片進行廣度優先遍歷（BFS），二次分類互不連通的同一屬性的三角面片，之后完成曲面分裂。

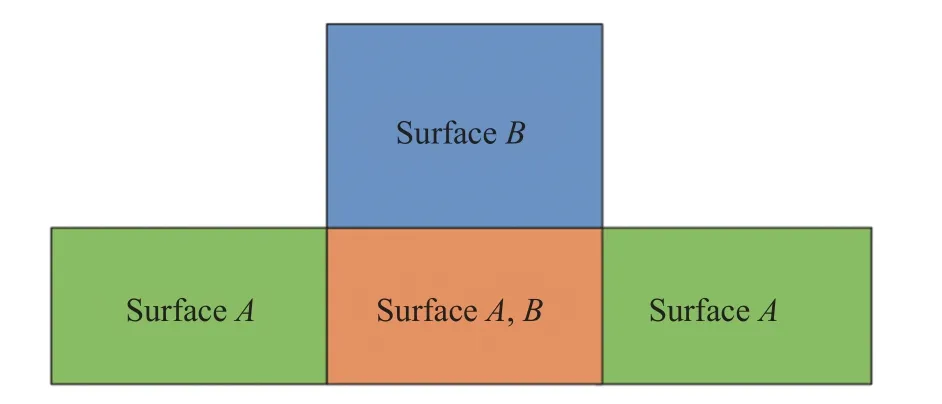
圖10 多區域情況Fig. 10 Situation of multiple regions

2.2.2 合并操作

頂點合并：若多個幾何頂點對應同一個端點，則刪除多余頂點，只留一個頂點完成頂點合并。

曲線合并：若多條曲線對應同一個邊界線段集合，則刪掉多余曲線，只留一條曲線完成曲線合并。

曲面合并：若多個曲面對應同一個三角面片集合，則刪掉多余曲面，只留一個曲面完成曲面合并。

在分裂及合并的基本操作的輔助下，本文采用自底向上的方法完成自動嵌入。根據表2 中的算法2，從低維到高維依次完成頂點的合并、曲線的分裂及合并、曲面的分裂及合并、部件的曲面索引更新，最終完成連續曲面的自動嵌入，得到用于網格生成的連續B-rep 模型。

表2 算法2 自底向上自動嵌入Table 2 Algorithm 2 bottom-up imprinting

圖11 展示了以嵌入后的B-rep 作為輸入，在其幾何上生成的網格結果，以驗證本文嵌入方法的有效性。可見曲面0 已被正確嵌入進曲面7，并保持了曲面0 中的邊界線段，生成了一致的保形網格。

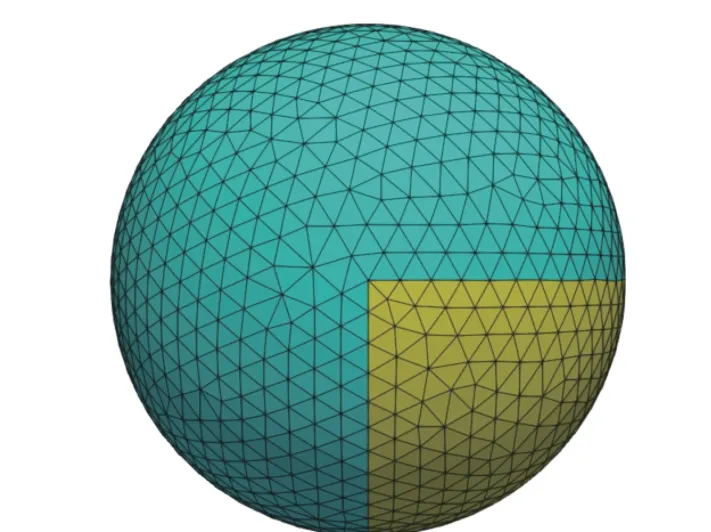
圖11 網格細節Fig. 11 Details of the generated meshes

3 數值驗證

3.1 曲面嵌入及網格結果

本文選取了某型號火箭、靶球和大壩三個典型裝配體CAD 模型對算法進行數值驗證，其分別包含13 個、115 個和1 884 個部件，模型網格如圖12 所示。分部件建模獲得的模型在不同部件的交界面處存在嚴重的幾何重疊及錯位，本文算法正確地消除了這些幾何干涉，輸出了幾何、拓撲一致的模型，并在此模型上生成了高質量的計算網格。

圖12 典型的裝配體模型Fig. 12 Typical assembly geometry

圖13 展示了各模型曲面嵌入及網格生成結果的局部細節。其中，火箭模型中，共檢測出1 656 處相交，曲面嵌入算法花費時間34 s；靶球模型檢測處15 177 處相交，曲面嵌入算法花費時間1 047 s；大壩模型中，共檢測出35 174 處相交，曲面嵌入算法花費時間1 553 s。其中，連續曲面嵌入過程中只涉及到拓撲操作，所耗費時間基本可以忽略（大壩例子所耗時間最多，但亦不足1 s）。

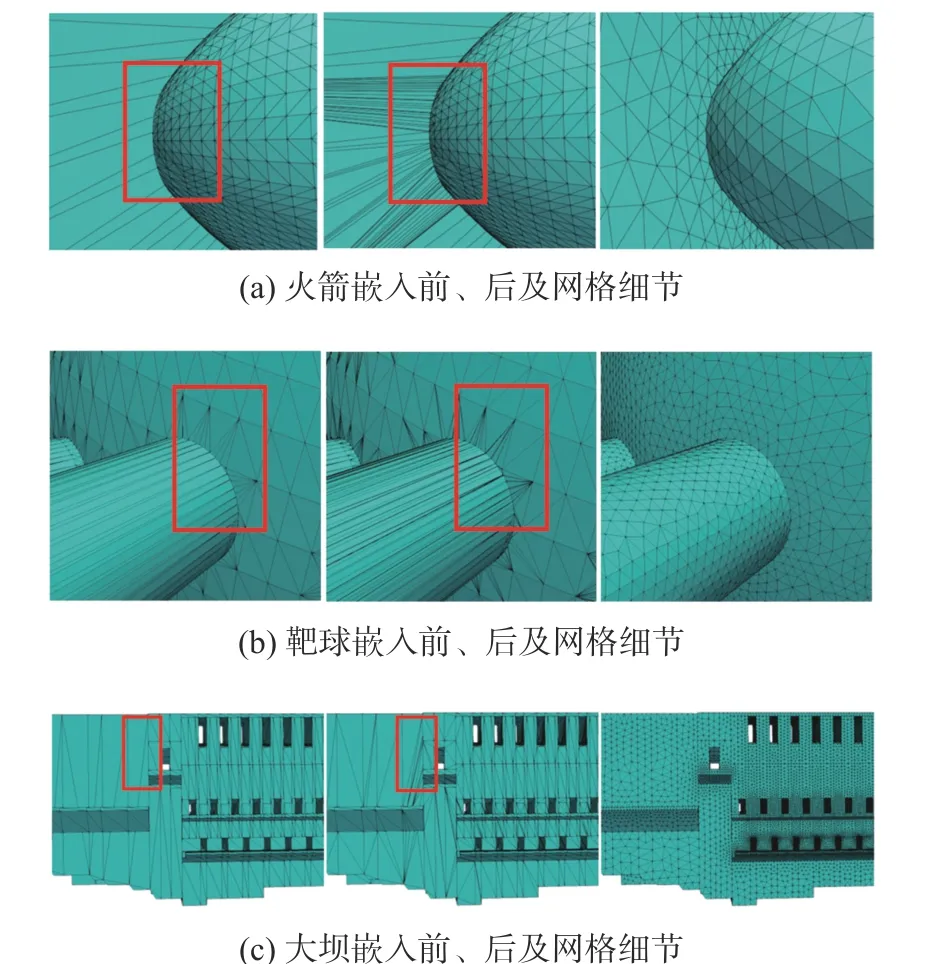
圖13 曲面嵌入及網格細節Fig. 13 Details of imprinting and meshes

本文方法時間花費主要在于離散曲面嵌入中的相交檢測及相交處理過程（邊界線段嵌入和邊界一致化處理）中，表3 統計了各個模型中此兩個過程中所耗費時間數據。大壩例子中因其最多的部件以及更多的錯位情形，其相交檢測時間花費占比也最高，約為25%左右，而另外兩個例子的占比分別約為6%和7%。

表3 時間統計Table 3 Statistics of time performance

曲面嵌入算法中涉及到曲面的分裂及合并操作，這些操作會引起模型曲面和曲線數量的變化。如圖3 情形中，將有發生1 次分裂、1 次合并，則曲面總數不變；如圖4 情形中則發生2 次分裂，1 次合并則會導致曲面數量上升。若是曲面完全重復情形，則只發生合并操作，則其導致曲面數量下降。本文中，輸入的火箭模型執行曲面嵌入算法后曲面和曲線數量保持不變，仍為124 張曲面和248 條曲線；靶球模型執行曲面嵌入算法后，曲面數由1 952 張曲面和4 739條曲線減少到1 768 張曲面和4 464 條曲線；大壩模型曲面數由14 322 減少到12 861，曲線數由31 676 減少到22 029。

以執行曲面嵌入后的CAD 模型以及適應模型幾何特征與用戶參數自動計算的單元尺寸函數為輸入，即可生成幾何與拓撲正確、單元形態和分布合理的高質量計算網格模型。針對火箭模型，測試中生成的曲面網格包含57 930 個三角形單元，實體網格包含102 569 個四面體單元；靶球模型的曲面網格和實體網格則分別包含5 146 056 和19 542 658 個單元；而大壩模型的對應數據為6 294 823 和45 620 136 個單元。

3.2 對比討論

如引言所述，曲面嵌入可分為直接在連續曲面Brep 上嵌入和在離散三角形網格上進行曲面嵌入，其相應代表有CADfix、libigl 及TetWild 等。本節中，我們將所提方法與上述程序進行了相關的對比以及討論。

CADfix 所提供的自動嵌入操作不能處理圖3 中這種部分嵌入的情況，需要通過布爾及分裂等操作完成最后的嵌入，該過程需要手工操作，對于圖3 所示簡單例子可迅速完成，但對于大壩和靶球這種復雜例子，所涉及繁瑣的手工操作往往令人難以忍受，因此本文算法的自動化具有明顯優勢。libigl 提供了一個在浮點誤差內比較穩定健壯的三角形相交算法，但無法引入誤差，在一些有狹小縫隙的地方無法完成嵌入，當然在相交中引入誤差本身是個十分棘手的難題。如圖14 與之相比，本文通過在邊界相交圖的計算中引入誤差，在曲面內部通過拓撲比較去除三角形相交，即可以正確完成在這些區域的自動嵌入。

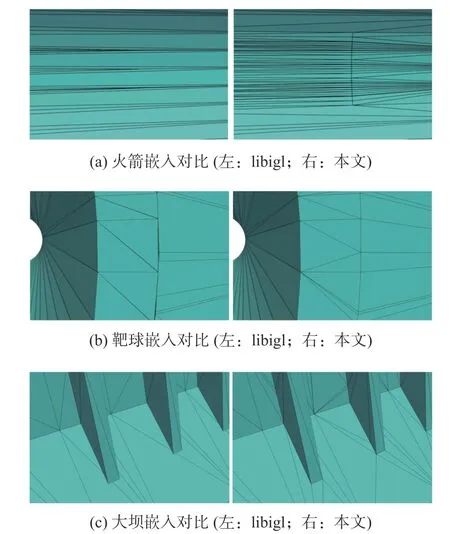
圖14 本文方法與libigl 嵌入對比Fig. 14 Comparison of imprinting between the proposed method and libigl

TetWild 通過四面體優化的方法來完成模型的嵌入及修復功能，并在該過程中引入誤差，控制修復的精度，該方法亦可適用于本文所選取模型，但是存在著兩個缺陷。其一，TetWild 的相交運算是在有理數的輔助下完成的，遠比浮點運算速度慢，另外四面體優化迭代過程也耗時較多；其二，TetWild 修復僅僅基于離散表征，其網格結果中可能出現“鋸齒”現象，使得網格精度降低。表4 統計了TetWild 和本文算法處理3 個模型所耗時間。對比表明，本文算法所耗時間明顯小于TetWild，且隨著模型規模的增大，本文算法時間優勢越來越凸顯，對于3 個測試樣例，TetWild 所耗時間是本文算法的2 倍以上。

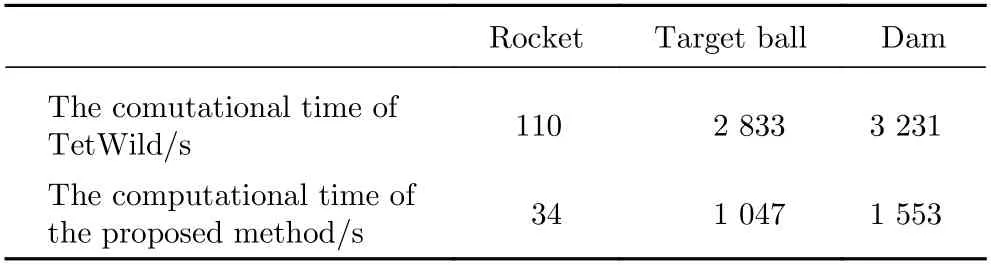
表4 時間對比Table 4 Comparison of computational time

此外，在火箭和大壩模型（誤差設置分別為0.5 mm和0.1 mm）中TetWild 出現了“鋸齒”現象，見圖15，而本文算法通過連續-離散的雙重表征，嵌入過程中保留了連續幾何精確的數學表達而僅僅改變了B-rep的拓撲，嚴格保證了模型的幾何精度。

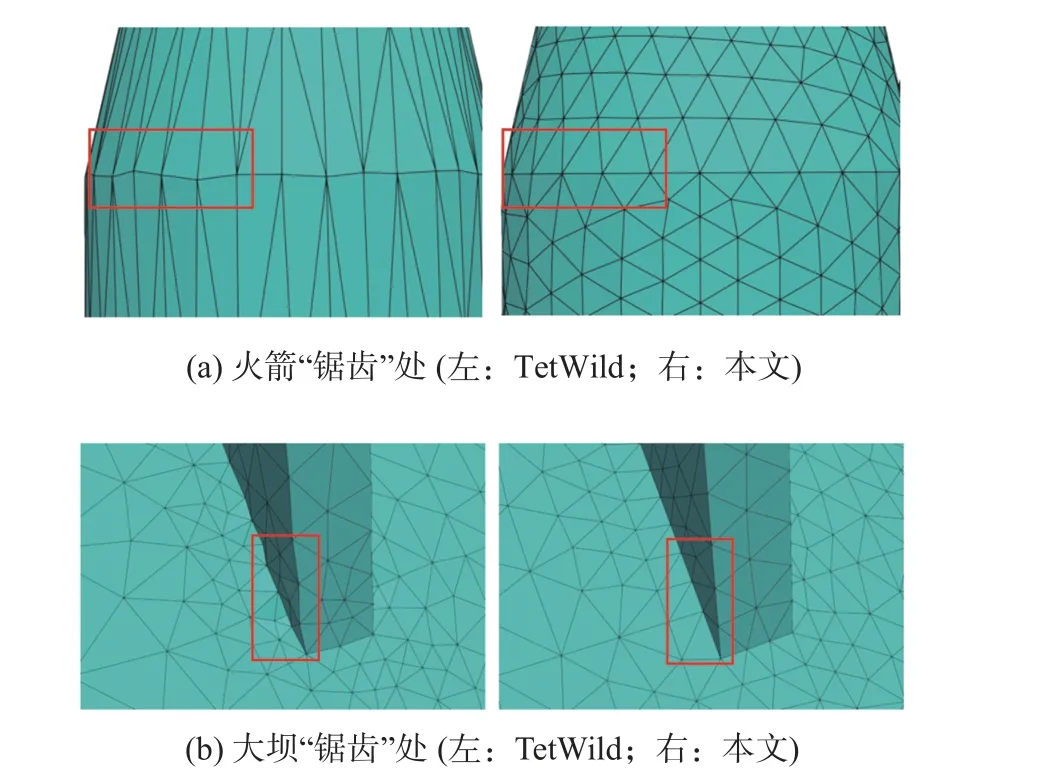
圖15 本文方法與TetWild 在“鋸齒”處對比Fig. 15 Comparison between the proposed method and TetWild in zigzag region

4 結 論

本文針對錯位裝配體在部件間重疊區域的多份表征問題，應用連續-離散混合曲面造型方法，開發了適用于分部件建模獲得的裝配體模型的自動曲面嵌入算法。在離散曲面上，通過引入誤差計算邊界線段-三角形相交以求得邊界相交圖，而后通過拓撲操作移除其余三角形相交問題，完成離散曲面嵌入；之后根據邊界相交圖及離散嵌入結果，在簡化的幾何引擎上設計了相應的曲線曲面分裂合并等操作，并在離散-連續映射關系的輔助下自動完成連續曲面B-rep上的自動曲面嵌入。在典型算例下用嵌入后的B-rep為輸入，以其網格生成結果驗證了該自動曲面嵌入算法的有效性。通過與其他嵌入方法的對比，展示了本文算法在自動化程度、嵌入有效性、精度保證及時間上的優勢。本文算法的主要優點有：

1）曲面嵌入中的幾何計算基于線性的離散模型，通過線段-三角形相交計算邊界相交圖，并運用拓撲比對移除三角形相交；

2）在離散-連續曲面的映射關系輔助下，根據邊界相交圖，在模型B-rep 上完成嵌入和合并操作，該過程不更改模型B-rep 的數學表達而只改變其拓撲，可有效保證嵌入后模型的幾何精度；

3）保證修復后裝配體模型B-rep 的正確性和一致性，可直接復用已有的基于B-rep 的主流曲面網格生成算法，生成保形的曲面網格。

本文算法目前尚不支持部件間互相貫穿的情形，在后續的工作中我們將嘗試在B-rep 上設置約束條件以處理貫穿情形下的曲面嵌入。