旋翼流動的塊結構化網格自適應方法

肖中云，郭永恒，張 露，崔興達

(中國空氣動力研究與發展中心，綿陽 621000)

0 引 言

旋翼尾渦是流體在旋轉槳葉作用下產生的一種特殊的旋渦流動現象，是由槳葉梢部脫出的集中渦和后緣脫出的尾跡面組成的流動演化系統，其中槳尖渦在尾跡流動中占據主導作用，是旋渦尾跡流場的骨架[1]。由于槳葉旋轉、揮舞等非定常運動特點，槳尖渦的生成及對后續槳葉的干擾產生嚴重的非定常氣動載荷，并誘發槳渦干擾（blade-vortex interaction,BVI）噪聲。當前，用CFD 方法模擬旋翼尾渦仍是一大難點[2-4]，通常旋翼槳尖渦直徑約為槳尖弦長的10%，而模擬槳尖渦的網格尺度則可能小到槳尖弦長的1%。由于空間網格尺度不足以匹配旋渦尺寸導致旋渦的數值耗散過大被抹平，影響到槳渦干擾相關的氣動載荷、噪聲預測的準確性。

自適應網格加密（adaptive mesh refinement, AMR）是解析局部流動特征的最有效方法之一，理論上可以根據流場特征對網格分辨率進行動態調整，是大范圍內模擬旋渦空間演化的理想方法。在傳統計算方法里面，多塊對接結構網格由于有嚴格的JKL 指標關系，很難實現網格的局部加密。非結構網格在數據結構上比較靈活，但網格加密后單元質量下降及網格信息存儲量大是其面臨的難題。笛卡爾網格由于具有空間網格正交和易于進行網格自適應加密等特點得到了較好發展[5-6]，被譽為是CFD 技術的未來發展方向之一。笛卡爾網格自適應目前有單元自適應和塊自適應（block structured AMR, SAMR）兩種方法。單元自適應根據流場計算需要對網格單元進行加密；塊自適應[7]指網格加密前后都具有塊結構化的特點，待加密區域不是單個的網格單元，而是規則的立方體區域。目前發展的自適應加密第三方庫中，采用單元加密方法的如libMesh[8]、P4est[9]等，采用塊自適應網格的如CHOMBO[10]、PARAMESH[11]和SAMRAI[12]等。這些三方庫將自適應網格加密和并行負載平衡等函數封裝為獨立模塊，將其與所解決的具體物理問題和算法隔離開來，在流體力學、天文學、宇宙學、地質學等多個領域得到了廣泛應用。

塊結構笛卡爾網格結合了笛卡爾網格與結構網格的優點。首先利用笛卡爾網格自適應能力強的特點，實現空間任意區域的網格自適應加密；其次網格具有結構化特征，就使得網格單元的相鄰關系尤其簡單，并且結構網格的一些高階重構計算方法能夠得到繼續使用，從而獲得較高的流場計算效率。本文從上述特點出發，探索了塊結構笛卡爾網格在旋翼計算中的生成方法，通過結構貼體網格加背景笛卡爾網格的雙網格技術構建計算域，發展了背景網格的幾何自適應技術和基于旋翼尾跡的流場自適應技術，采用該方法在UH-60A 旋翼上構建了懸停和前飛流場的自適應網格，表明當前方法的可行性。

1 塊結構笛卡爾網格生成

1.1 笛卡爾網格劃分方法

塊結構笛卡爾網格劃分方法如圖1 所示。首先定義包圍整個計算域的初始長方體網格塊，該網格塊內網格為三個方向均勻正交排列的笛卡爾網格，網格間距分別為（ Δx,Δy,Δz），并且約定每個方向的網格單元個數為偶數。網格生成是網格塊不斷細分的遞歸過程，當判定一個網格塊需要加密時，該網格塊在每個坐標方向上一分為二。這樣經過一次網格細分，二維情況下一個網格塊被分裂為四個網格塊，三維情況下一個網格塊被分裂為八個網格塊。新產生的子網格塊在三個方向上的網格維數同父網格保持不變，網格間距縮小為原來的1/2，當父網格塊在某個方向的網格單元數為偶數的情況下，子網格塊在這個方向上正好兩個單元對應父網格塊的一個單元。圖1 顯示了笛卡爾網格劃分的前三層網格，其中第三層網格只對第二層的一個網格塊進行了加密，這樣第一、二、三層網格的網格塊數分別為1、8、8 塊，總的網格塊數為17 塊。

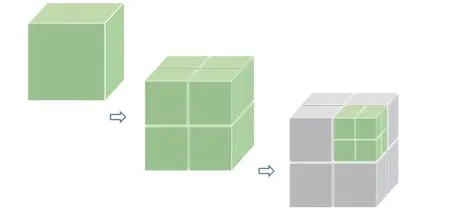
圖1 塊結構網格劃分方法示意圖Fig. 1 Schematic of block structured grid splitting

根據上述網格劃分特點，三維笛卡爾網格塊采用八叉樹數據結構進行管理。如圖2 所示，八叉樹的每個節點表示一個正方體的體積元素，頂部節點稱為根節點，也是體積最大的節點。每個節點有八個子節點，這八個子節點所表示的體積元素加在一起就等于父節點的體積。沒有后代的節點稱為葉子節點，八叉樹葉子節點代表了分辨率最高的情況。例如將空間某個區域的分辨率設成（ Δxt,Δyt,Δzt），那么覆蓋該區域的網格塊將不斷細分，直到每個葉子網格間距將小于目標值為止。八叉樹的葉子節點覆蓋了整個計算域，圖2 顯示的葉子節點個數為15。一般情況下流場計算只需要在葉子節點上進行，當采用多重網格等加速收斂計算方法時，中間節點及根節點可以參與到計算中。

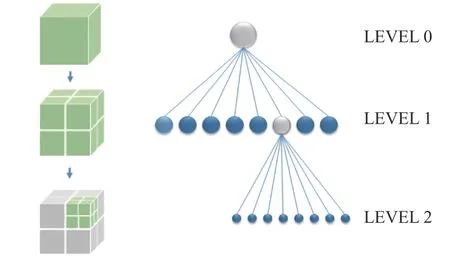
圖2 八叉樹數據結構示意圖Fig. 2 Schematic of octree data structure

采用上述方式生成的塊結構化笛卡爾網格有很多優點。首先是網格描述非常簡潔、存儲量極小，初始網格定義了網格塊中心點坐標和三個方向的尺度及網格間距，新生成網格塊層級和中心點坐標由上一級網格塊得到，其他信息如網格點坐標、單元體積、單元面積等都可以直接用解析式給出。這樣不需要存儲每個網格點的信息，從而大大減少對內存的需求。其次是和結構化網格一樣，塊結構化的笛卡爾網格流場變量按指標順序連續存放，有利于充分利用高速緩存提高存取效率，并且非常容易在三個方向上構造高階插值模板單元，以很小的成本代價實現高階格式。再次，塊結構笛卡爾網格由粗網格不斷細分得到，子網格和父網格之間構成多重網格的嵌套關系，可以根據此關系設計多重網格方法，提高流場計算的收斂速度。

1.2 多層空間填充Z 曲線

當前自適應網格方法可以簡單地類比于給網格增加或減少補丁，加補丁就是給網格加密，揭補丁就是使網格稀疏。空間填充曲線技術是為了高效存儲和管理空間網格的一種方法，它的目的是將多維空間數據轉換到一維空間上，并通過轉換后的一維空間索引值存儲和查詢多維數據。除了有降低維度的特性外，空間填充曲線還具有數據聚類特性，其特點是將空間上鄰近的網格單元映射為一維曲線上盡可能接近的點，因此只需要訪問查詢點的鄰近點，就能夠獲得網格單元的最近鄰單元。常用的空間填充曲線有Z 曲線[13]、Hilbert 曲線和Gray 曲線等，其中Hilbert 曲線和Gray 曲線涉及到方向旋轉，映射過程比較復雜，聚類特性更優。相比之下Z 填充曲線的映射過程比較簡單，幾何空間的網格相鄰關系更容易確定而被網格方法所廣泛采用。本文針對自適應網格特點將空間填充Z 曲線進行了多層表示，即填充曲線包含了葉子節點、它們的父節點及根節點等全部網格，將所有網格層展開后得到網格關系如圖3 所示。保留非葉子節點網格的目的是能夠自由地對網格進行加密或者稀疏變換，從圖3 可以看到，通過延拓或者插值計算，LEVEL 1 和LEVEL 2 的流場信息交換是非常方便和直接的。圖3 同時給出了表示多層網格的空間填充Z 曲線。其編碼規則如下，編碼首先從根節點開始，對于任何一個節點，首先判斷其是否存在子節點，如果有則指向子節點，如果沒有則指向同一級的鄰居節點，鄰居節點之間用Z 曲線連接，當子節點為Z 曲線最后一個節點時回到父節點。注意這里的節點不重復計數，如圖3 中當出現節點5 指向節點1 時，由于節點1 已經存在于序列中而略過，因此5 的下一個節點為6。當采用上述方式索引以后，可以看到，任一節點的鄰居節點可能是兄弟（相同父節點），也可能是堂兄弟（父節點兄弟的孩子），但總的來說，仍具有鄰居節點位于空間填充曲線附近的聚類特性。

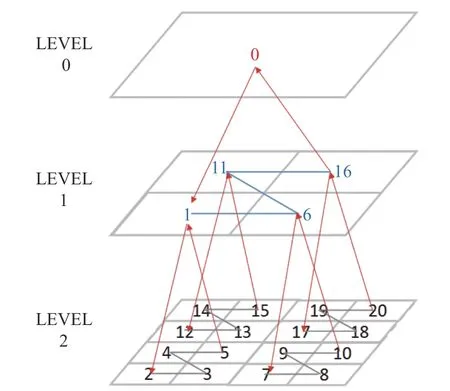
圖3 多層網格的Z 填充曲線Fig. 3 Z filling curves of multi-layer grids

在用空間填充曲線進行排序以后，對網格進行并行分區、滿足負載平衡就變得非常簡單，由于每個網格塊的網格單元數相同，因此滿足負載平衡的并行分區只需要將一維的空間填充曲線進行等量剖分就可以了。當然也可以考慮到葉子節點和非葉子節點之間計算量的差異，給不同節點賦予不同的權重，采用加權平均的方法進行分區。圖4 顯示了將21 個網格塊分配到5 個進程的分區情況。

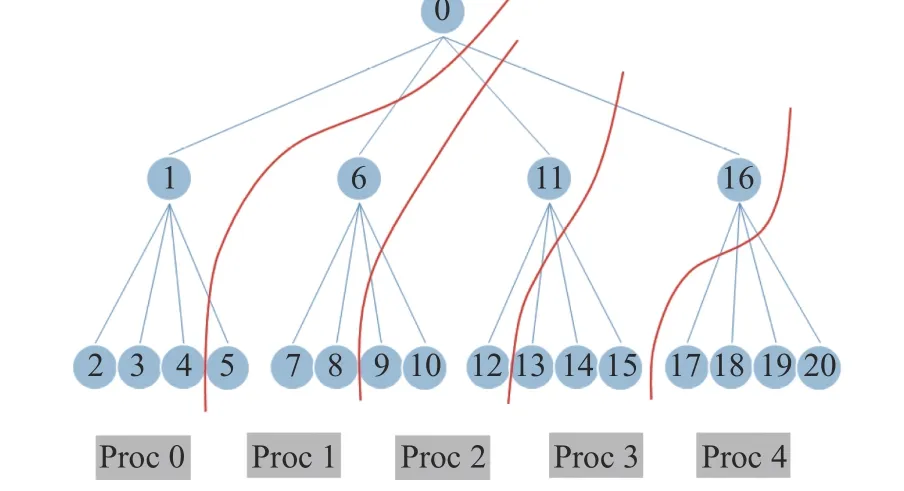
圖4 多層網格的并行分區Fig. 4 Parallel partition of multi-layer grids

1.3 網格加密判則與加密方法

采用一分為八的方式加密網格將導致網格量呈幾何級數增長。為了讓網格總量可控，本文采取的策略一是限制網格最大層數，一旦網格層級超過最大值則加密被終止，二是建立合適的加密準則，將網格加密局限在幾何復雜、流動變化劇烈的局部區域，并且網格隨流動特征變化的自適應加密。

限制網格最大最小層數的作法實際上是限制了網格單元的最大最小尺寸，最大尺寸規定的是遠場的網格尺度，與計算域的大小相關；最小尺寸規定的是模擬流動特征的網格最小尺度，比如對于旋翼流動來說，網格加密是為了實現槳尖渦的模擬，因此可以根據槳尖弦長測算出槳尖渦的渦核直徑，并由此估算出能夠較好捕捉旋渦的網格最小尺度。

網格的局部加密包括了基于幾何特征加密和基于流場特征加密兩種類型。旋翼模擬一般將笛卡爾網格作為背景網格，笛卡爾網格與近場網格之間構成重疊關系，此時近場外邊界網格尺度就作為重疊區笛卡爾網格加密的目標尺度。流場特征加密主要是基于旋翼槳尖渦的識別與局部加密，目前旋渦識別方法發展有很多種[14-15],常見的Q-判據定義方法如下：

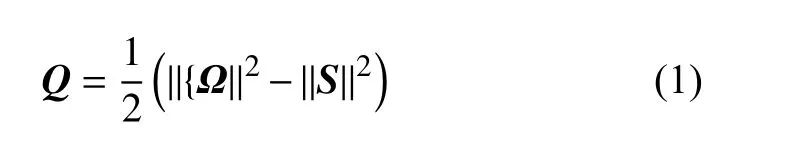
其中 Ω表示旋轉張量，S表示變形率張量。為了防止網格密度變化過渡劇烈，限定相鄰笛卡爾網格塊的網格尺度相差最大一倍。即當對某一網格塊進行加密時，還需要判斷該網格塊的相鄰塊是否存在密度差大于一倍的情況，如果存在，則該相鄰塊也被列入到待加密列表中，以此類推，直到所有塊都滿足條件為止。需要注意的是，這里所謂的相鄰塊包括了面相鄰塊、棱線相鄰塊和角點相鄰塊。對于長方體來說，相鄰塊的數量最多情況下達26 個。圖5 以二維為例對網格加密過程進行了說明，圖5（a）顯示了待加密網格塊（用十字虛線表示），同時識別出周圍三個網格塊存在密度差大于1 倍的情況（桔色顯示）；圖5（b）對（a）中桔色顯示的三個網格塊進行了加密，同時又識別出周圍兩個網格塊存在密度差大于1 倍的情況；圖5（c）為最終的網格加密情況，可以看出每組相鄰塊的網格密度最大相差1 倍；圖5（d）為加密后網格的空間Z 曲線填充情況。圖5（d）只對葉子節點進行了空間填充的Z 曲線顯示，顯示多層網格的Z 填充曲線如圖6 所示。從圖中可以看到，當前網格一共包含了5 層，除了最后一層全部是葉子節點外，其他層凡是有向下箭頭線的均為非葉子節點，即表明當前塊有更細的網格剖分。圖5（d）可以理解為圖6 在平面內的投影，并且刪除非葉子節點后得到的圖形，這些非葉子節點不直接參與流場計算，但在方便網格組織與自適應加密中起到作用。

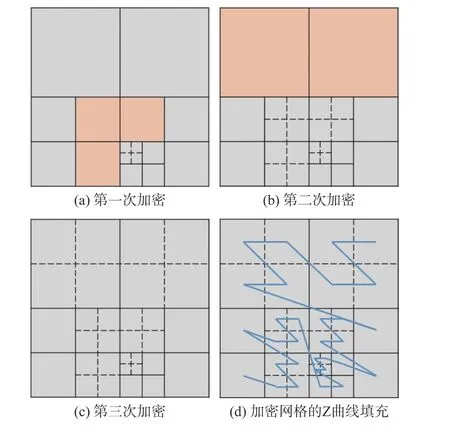
圖5 網格加密過程示意圖Fig. 5 Schematic of mesh refinement

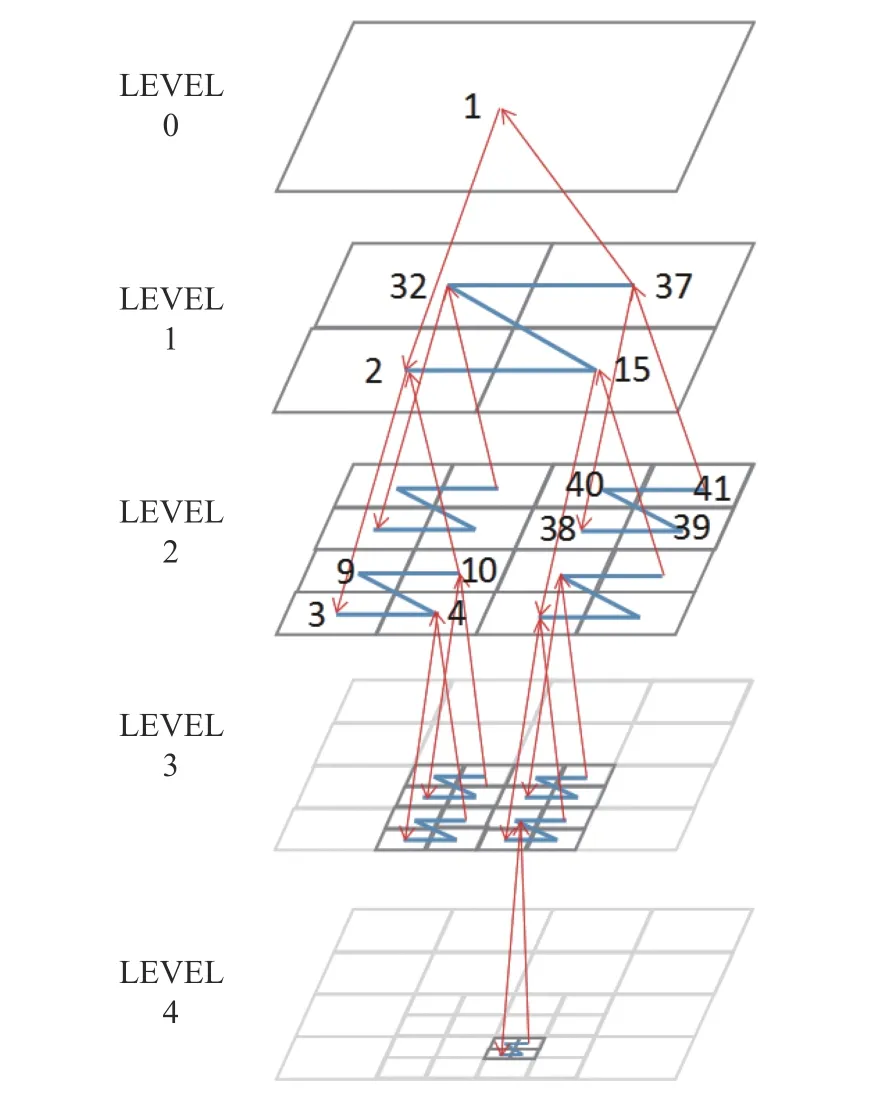
圖6 局部加密網格的Z 填充曲線Fig. 6 Z filling curves for local mesh refinement

2 算例與分析

2.1 旋翼近場貼體網格

為驗證網格模型，本文選擇生成UH-60A 旋翼的計算網格，模擬狀態包括旋翼的懸停狀態和前飛狀態。UH-60A 旋翼共包括四片槳葉，旋翼半徑R=8.178 m，槳葉展弦比15.5，槳葉具有非線性扭轉、槳尖后掠等現代旋翼特征。槳葉貼體網格采用多塊對接結構網格（見圖7），其中槳葉剖面拓撲結構為O 型，槳葉表面網格為四邊形單元，物面邊界層區域采用大拉伸比網格進行刻畫。

從圖7 中可以看到，旋翼網格分為了4 個相對獨立的子網格，由于槳葉在一周旋轉運動過程中，即使是剛性假設槳葉，也需要進行旋轉、揮舞、變距等運動，槳葉與槳葉之間的相對位置會發生變化，將單片槳葉網格獨立作為一個子網格，這樣就可以讓槳葉網格隨槳葉一起運動，每個時間步的子網格變化通過多次旋轉變換得到。近壁區流場計算由貼體網格負責進行，背景網格深入到壁面的部分經過重疊挖洞以后被當作洞內點不參與計算。

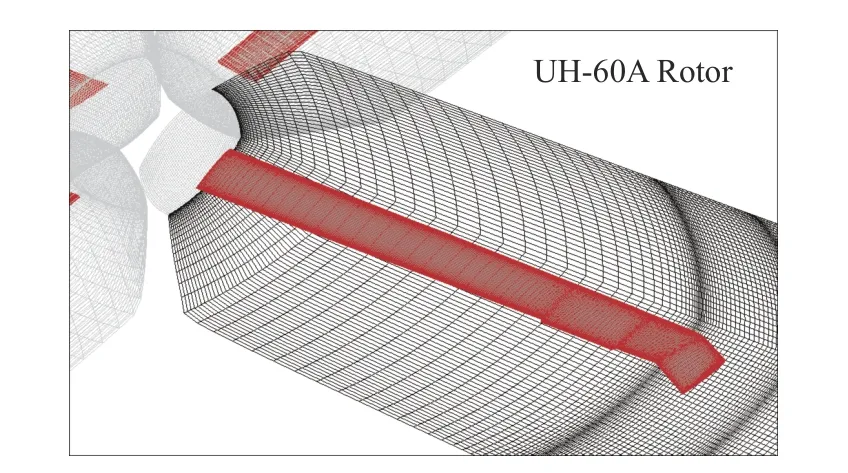
圖7 槳葉貼體網格Fig. 7 Body fitted grids of the blade

2.2 背景網格重疊邊界的幾何自適應

在生成近場貼體網格以后，背景網格采用笛卡爾網格生成方法，即采用雙網格技術構建流場計算網格。兩組網格的計算域劃分如圖8 所示，考慮到當前旋翼半徑R= 8.178 m，定義背景網格的外廓尺寸為x,y,z∈[-50 m, 50 m]的立方體區間，網格加密層級定義為9 級，這樣最小網格單元尺度約為 Δx=0.048 m。圖中立方體代表的是初始笛卡爾網格塊，塊內每個方向的網格單元個數為8 個。

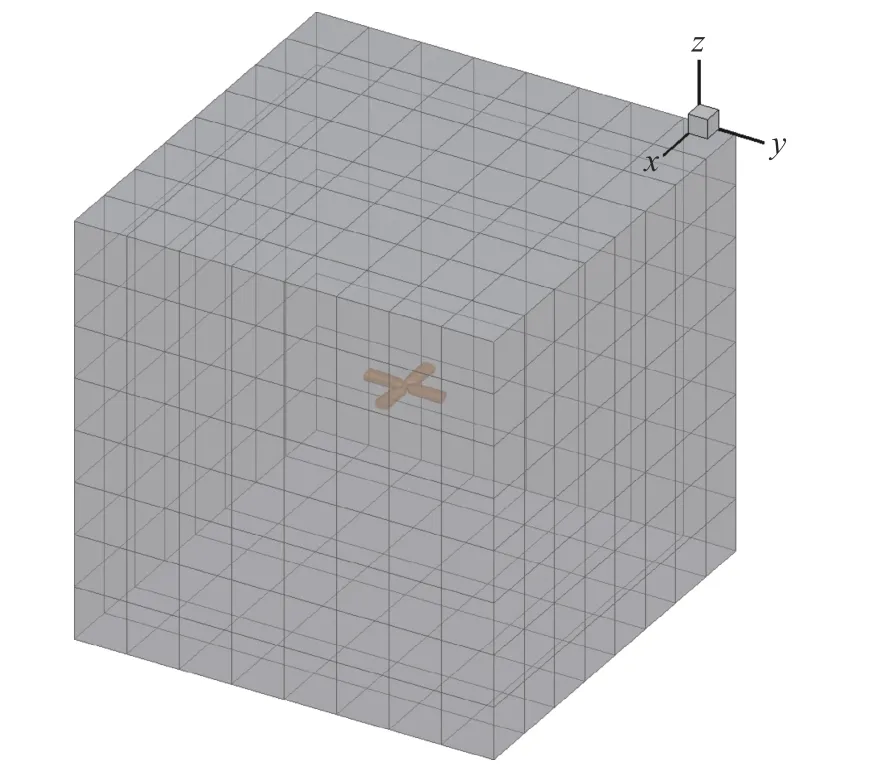
圖8 貼體網格與背景網格Fig. 8 Body fitted and background grids

背景笛卡爾網格具有能夠自動生成的特點，從圖8 所示的初始笛卡爾網格塊開始，不斷對網格進行細分，直到核心區域網格密度滿足模擬要求為止。在這里背景網格與貼體網格之間構成重疊關系，要求重疊區域兩組網格的網格尺度相當，因此該過程也被稱之為網格幾何自適應。由于背景網格要滿足與貼體網格重疊插值的條件，這里以貼體網格的外邊界作為特征對象，對背景網格塊依次進行判斷，如果特征對象與網格塊相交或者完全落在網格塊的內部，則判定該網格塊為待加密網格塊。對初始網格塊來說，定義網格層級LEVEL 0，在經過一次加密后生成8 個子網格塊，定義為LEVEL 1，以此類推，直到網格塊的網格尺度小于特征對象的網格尺度為止。圖9 顯示的是經過幾何自適應以后得到的笛卡爾背景網格分布，可以看到經過不斷細分以后，網格密度大的區域向近場集中；此外網格呈塊狀分布，塊內部網格均勻分布，相鄰網格塊的網格間距比值最大為2：1。圖10 顯示了背景網格和貼體網格交界區域的網格分布。可以看到背景網格在槳葉根部和尖部都進行了加密，在子網格外邊界區域，加密準則要求背景網格與貼體網格的網格尺度相當，滿足重疊插值對網格的要求。

圖10 近物面區域的網格分布Fig. 10 Grid distribution in the near wall region

2.3 基于旋翼尾跡的流場自適應

除了前面的幾何自適應以外，發展自適應網格的主要目的是根據流場特征對網格進行局部加密。為驗證網格對旋翼流場的自適應能力，本文將通過尾跡模型方法得到尾跡分布作為流場特征，對背景網格進行局部加密。

2.3.1 旋翼懸停狀態

懸停模擬狀態為旋翼轉速Ω= 255 r/m，拉力系數CT=0.0069。旋翼尾跡用Landgrebe 尾跡模型表示，具體公式如下：

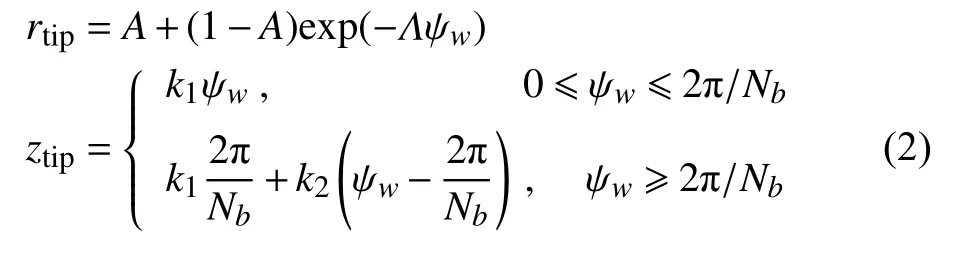
其中：rtip、ztip分別表示槳尖渦的無量綱徑向位置和旋翼軸向位置（用旋翼半徑R無量綱化），Nb表示旋翼槳葉片數， ψw為槳尖渦尾齡角， θtw為槳葉線性扭轉角，其他系數定義如下：

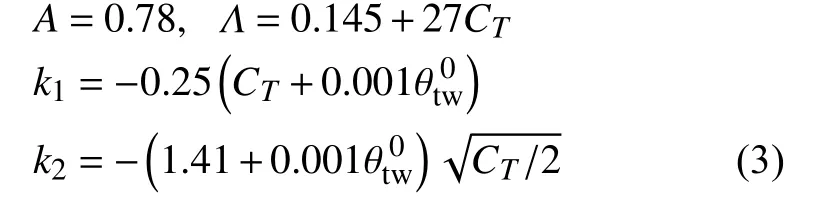
圖11 為Landgrebe 尾跡模型計算得到的旋翼懸停狀態下單片槳葉的槳尖和槳根尾跡分布，可以看到槳尖和槳根渦呈螺旋狀向旋翼下方發展，槳尖渦的下降速度更快，并且在下降的同時還向內收縮，最終穩定在約0.7 倍旋翼半徑位置處。

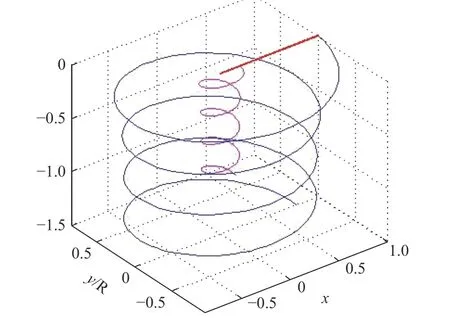
圖11 懸停狀態的槳尖和槳根渦線Fig. 11 Root and tip vortex lines of the blade in hover

加密準則是一旦尾跡線穿過網格塊，則定義該網格塊為待加密網格塊，直到網格密度小于目標網格密度為止。這里定義目標網格密度為槳尖弦長的2%。圖12 為懸停狀態下的自適應網格分布，可以看到在分布有尾跡線的地方，網格均進行了局部加密。由于模擬旋渦的網格尺度要小于槳葉子網格外邊界的平均網格尺度，因此，當地笛卡爾網格的分布更密更集中，遠小于重疊區附近的網格尺度。

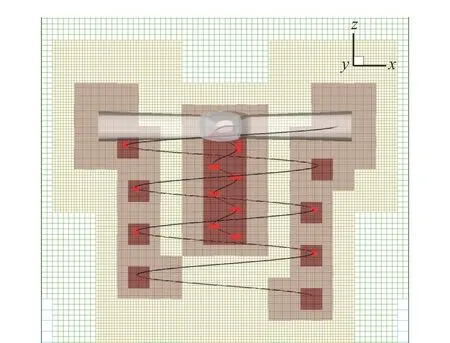
圖12 懸停狀態的自適應網格加密Fig. 12 Adaptive mesh refinement of the rotor in hover

2.3.2 旋翼前飛狀態

前飛模擬狀態為UH-60A 旋翼的C8534 前飛狀態，該狀態對應UH-60A 旋翼的大速度中等過載飛行狀態：其中拉力系數CT=0.0069， 槳尖馬赫數Mtip=0.642 ，前進比 μ=0.368， 槳盤傾角αs=-7.31°。

旋翼前飛狀態尾跡用Beddoes 預定尾跡模型[16]表示，該模型給出了尾跡分布的代數表達式，為研究旋翼尾跡分布以及槳渦干擾BVI 現象提供了方便。Beddoes 預定尾跡模型中包含了尾齡角 ψw和槳葉方位角 ψb， μ為前進比。渦元的軸向位移z則由旋翼軸向速度和局部誘導下洗速度積分組成，則槳尖渦尾跡幾何形狀可表示為：

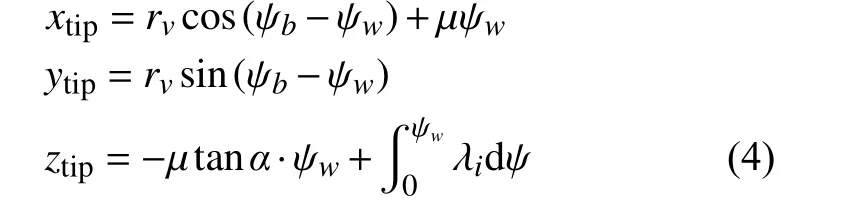
其中，xtip、ytip、ztip為槳尖渦尾跡的笛卡爾坐標，用旋翼半徑R無量綱化，坐標原點位于旋翼中心。rv為控制槳尖渦卷起及隨渦齡角向內收縮的徑向位置參數， μ為前進比，α為來流迎角， λi為當地誘導入流比，計算公式如下：

其中： λ0為 平均誘導入流比，E為尾跡傾斜角度參數。

圖13 給出的是UH-60A 旋翼前飛狀態下的槳尖尾跡分布三維視圖，由Beddoes 預定尾跡模型計算得到。可以看到在前飛狀態下，旋翼尾跡呈螺旋狀朝旋翼后下方發展。研究表明，旋翼槳尖渦的渦核直徑為槳尖弦長的1/10 量級，模擬槳尖渦所需網格的長度尺度約為槳尖弦長的1/100 量級，并且槳尖渦的分布范圍很廣，給傳統數值模擬方法的網格生成帶來了極大挑戰——采用近場全局均勻加密方法導致網格量不可承受，必須發展網格當地加密的自適應生成技術。

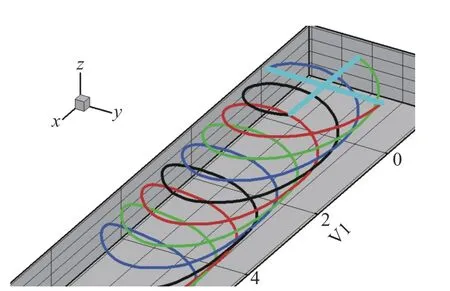
圖13 前飛狀態的槳尖渦線Fig. 13 Tip vortex lines of the rotor in forward flight

網格最大加密層數設置為9 層，由于網格加密的密度要求高，尾跡線分布范圍廣，最終網格塊數達到了4.4×104塊，網格單元數達到2.25×107。加密運算以單個進程串行方式完成，在主頻3.2G 的Intel I7-8700 CPU 芯片運算網格加密時間約為76 s。圖14是旋翼前飛狀態下的自適應網格分布，可以看到當前網格加密方法適應了尾跡線的分布情況，在旋翼的后方和下方區域對網格進行了加密，在槳尖尾跡線穿過的地方網格密度達到最大值。

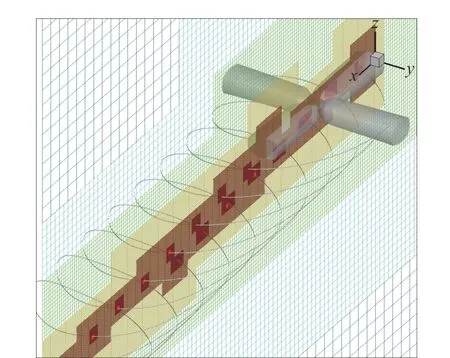
圖14 前飛狀態的自適應網格加密Fig. 14 Adaptive mesh refinement of the rotor in forward flight

圖15 用分層方式顯示了旋翼附近的網格，位于中間的第6～7 層網格是在前5 層網格上的疊加，位于右邊的第8～9 層網格又是在前7 層網格基礎上的疊加；最大網格密度位于槳尖渦尾跡附近，為尾跡流動的精細模擬創造了條件。

圖15 自適應網格的多層結構Fig. 15 Multi-layer structure of adaptive mesh refinement

圖16 給出了旋翼前飛狀態自適應網格的第8 層網格分布，網格最大層級為9 層，第8、第9 層代表了網格的核心加密區，可以看到這些密網格分布在旋翼附近及旋翼后下方區域。圖中不同顏色代表網格塊所在的不同分區，分區方法利用空間填充Z 曲線的聚類特性，使分在同一個進程的網格塊保持相鄰。同時需要注意的是由于空間填充Z 曲線在結束一個Z 遍歷以后有跳躍的特點，前一個Z 的最后一個網格塊與后一個Z 的第一個網格塊并不相鄰（見圖5（d）），因此可能出現分在同一個進程的網格塊不相鄰的情況，有研究[17]表明在同一個進程內，不相鄰的網格塊最多為兩組，這樣保證了網格塊不過于分散，降低了并行發送與接收方面的需求。

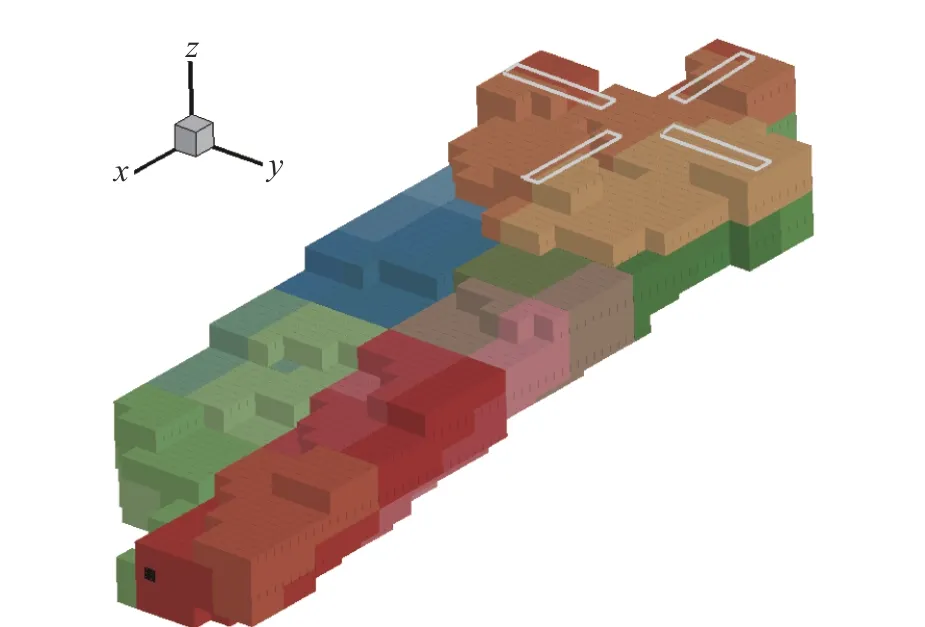
圖16 塊結構笛卡爾網格的并行分區Fig. 16 Parallel partition of the block structured Cartesian grids

3 結束語

本文探討了旋翼計算中背景笛卡爾網格的生成方法，發展了塊結構化笛卡爾網格的生成技術。將該技術應用在UH-60A 旋翼上的懸停和前飛流場，獲得了網格密度分布合理的自適應網格，主要結論如下：

1）采用雙網格建模思路，背景笛卡爾網格由于不需要適應物面邊界，網格劃分過程十分快捷高效。背景網格可以通過幾何特征或流場特征對網格進行自適應加密，使當地網格密度滿足重疊插值或流場計算的要求。

2）塊結構自適應笛卡爾網格采用多層網格結構，高效實現了網格的加密和稀疏操作。用八叉數數據結構行管理網格塊，相對于傳統笛卡爾網格管理網格單元而言，整個八叉數所管理的節點數大大降低，提高了整個數據結構的管理效率。

3）采用多層空間填充Z 曲線遍歷網格，利用該順序對網格塊進行編號和并行分區，分區方法利用空間填充Z 曲線的聚類特性，使分在同一個進程的網格塊盡可能保持相鄰，降低了并行發送與接收方面的需求。