廣義估計方程與混合線性模型在Python中的實現

焦奎壯，馬煦晰，馬小茜，劉朝屹，張 青，馬 露

武漢大學公共衛生學院（武漢 430071）

縱向數據是流行病學研究中最常見的資料類型之一，常見于隊列研究、定群研究等研究設計中。這些研究設計中暴露因素或健康結局指標均具有隨時間變化而變化的特點，為探索暴露因素與健康結局間的關系，往往需對研究對象進行隨訪或重復測量。針對同一研究對象的多次測量，研究結果間通常存在相關關系，若不滿足獨立性的條件，不適用一般線性模型或廣義線性模型，且當觀測值存在缺失時，重復測量方差分析也不適用。因此，廣義估計方程（generalized estimating equations，GEE）和混合線性模型（mixed linear model，MLM）被廣泛應用于縱向數據的統計分析。目前，主流的統計分析軟件如SAS、SPSS和R等均能實現GEE和MLM的建模分析[1-3]。Python作為一款開源免費軟件，因其強大的大數據處理第三方庫（Pandas、Numpy、Scipy等）、內存優化系統和豐富的應用場景（爬蟲等），可方便快速地實現數據的獲取、清洗、管理和分析，顯著縮短數據分析時間[4-5]，近年來越來越受到國內科研工作者的歡迎。隨著我國醫療系統信息化建設的快速推進，醫療大數據的智能化統計分析是必然的發展趨勢[6]。運用Python軟件實現流行病學研究中的統計分析，目前尚不多見。本研究以Python 3.8.5中的statsmodels庫為例，通過研究實例介紹GEE和MLM在Python軟件中的實現方法。同時，采用R 4.0.5軟件中的geepack包和lmerTest包構建GEE與MLM模型[7]，作為本次Python結果的對照，驗證Python輸出結果是否正確。

1 資料與方法

1.1 資料來源

為研究某地區大氣顆粒物PM2.5對肺功能的影響，收集該地區連續十日的日均PM2.5濃度、溫濕度和研究對象的肺功能數據。其中，PM2.5濃度、溫濕度數據分別來自武漢市生態環境保護局（http://hbj.wuhan.gov.cn/）和湖北省氣象局（http://hb.cma.gov.cn/），均采用Python爬蟲收集。

采用方便抽樣方法抽取研究對象，使用第1秒用力呼氣容積（forced expiratory volume in one second，FEV1）作為肺功能評估指標，使用肺功能測試儀于每日7:30 AM由研究對象自測，測量10日后通過軟件將數據讀入計算機。以某位研究對象（20歲）為例，顯示十天連續測量數據，詳見表1。

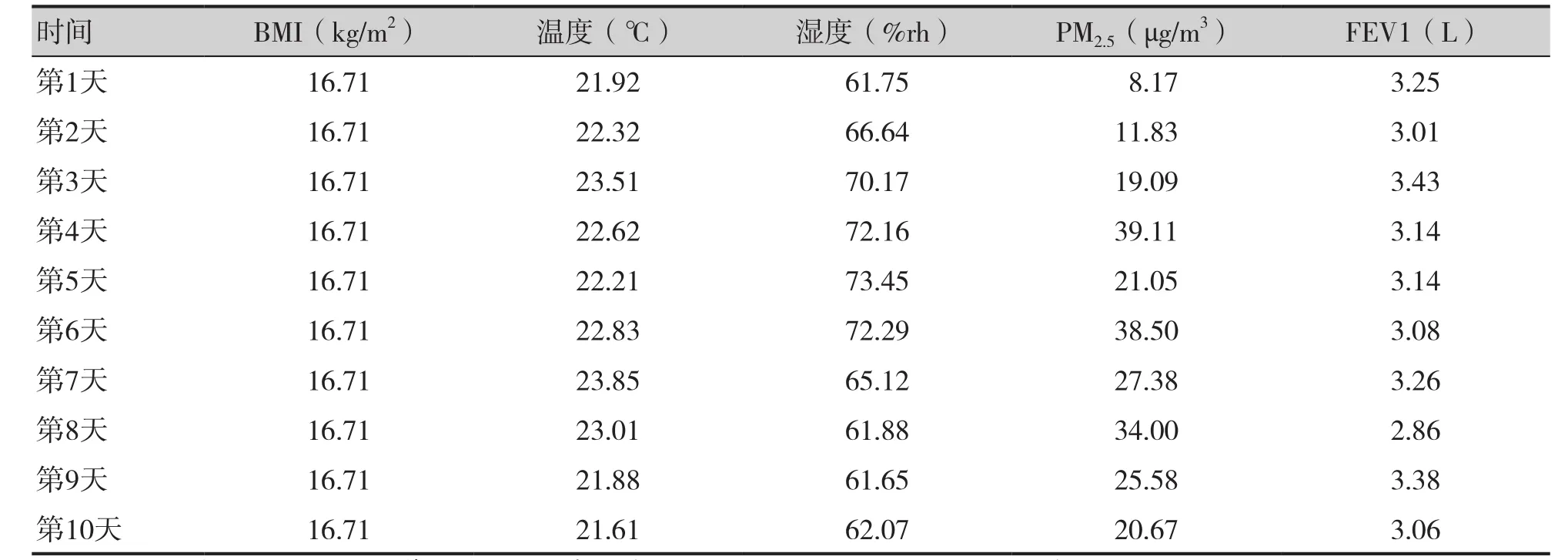
表1 連續10日顆粒物、氣象及研究對象數據資料Table 1. Data of particulate matter, meteorology and research objects in ten consecutive days

1.2 模型構建

本研究通過控制研究對象年齡、BMI和大氣溫濕度，評價PM2.5對研究對象肺功能的影響，以PM2.5單污染物滯后2天的暴露模型為例展示GEE與MLM在Python軟件中的實現。

1.2.1 GEE模型構建

GEE模型是Liang 和 Zeger于1986年在擬似然的基礎上對廣義線性模型的推廣，旨在分析縱向數據中因素對總體平均水平的影響[8-10]。本研究以FEV1為因變量，記為Yij，表示有i個研究對象（1，…，n），每個研究對象有j個觀察值（1，…，p），協變量記為Xij。構建如下模型：

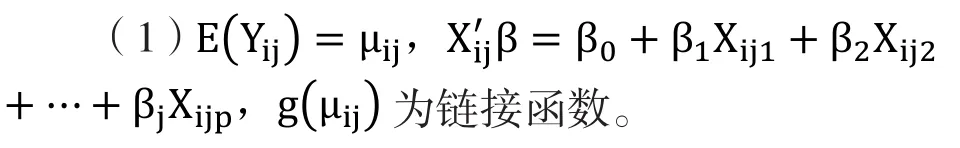
建立Yij與Xij間的函數關系，鏈接函數的選擇主要有以下幾種形式：①因變量服從正態分布，鏈接函數選擇identify；②因變量服從二項分布，鏈接函數選擇logit；③因變量服從泊松分布，鏈接函數選擇log；④因變量服從負二項分布，鏈接函數選擇negativebinomial。

（2）Var(Yij) = v(μij)·φ，建立 Yij的方差與均值間的函數關系。

（3）Ri(α)是Yij的作業相關矩陣，表示因變量各次的重復測量值間的相關性大小，作業相關矩陣包括以下幾種形式：①可交換，又稱等相關，即任意兩次不同時間的觀測值間相關是相等的；②相鄰相關，即只有相鄰時間的兩次測量值之間具有相關性；③自相關，即相關與間隔次數有關，相隔次數越長，相關關系越小；④不確定型相關，即相關矩陣非對角線上的元素均不等；⑤獨立，即因變量之間不相關。

根據Liang和Zeger的定義，構建如下 GEE模型：

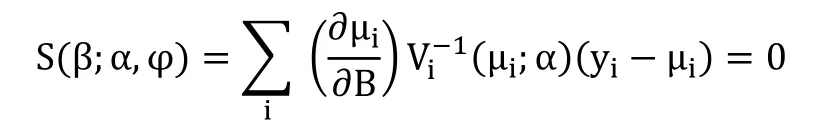
Vi是Yi的協方差矩陣，。根據給定的α和φ的估計值，通過迭代重復加權，采用最小二乘法，求解上述方程，最后得出β的一致性估計。

1.2.2 MLM模型構建

MLM是一般線性模型（Y = Xβ + ε）的拓展[11-12]，其保留了傳統線性模型中的殘差需滿足正態性的假定，而對獨立性與方差齊性不做要求[13]，引入隨機效應部分 Zγ，可表達為：Y = Xβ + Zγ + ε，Y表示因變量測量值的向量，X為固定效應設計矩陣，β為固定效應參數向量，Z為隨機效應設計矩陣，γ為隨機效應參數向量，服從均值向量為0、方差/協方差矩陣為G的正態分布，表示為γ～N(0，G)，隨機效應主要有以下三種[14-15]：①隨機回歸系數帶來的隨機效應；②隨機截距帶來的隨機效應；③隨機回歸系數和隨機截距帶來的隨機效應。ε為隨機誤差向量，服從均值向量為0、方差/協方差矩陣為R的正態分布，即ε～N(0，R)。

1.3 模型驗證

采用R4.0.5軟件的geepack包、lmerTest包分別構建GEE與MLM模型，作為參照，驗證Python輸出結果是否正確。

2 結果

2.1 GEE建模及參數估計結果

本研究因變量FEV1為定量連續數據，服從正態分布，故鏈接函數選擇identify，根據以上定義，可構建如下GEE模型：

β0為截距，β1、β2、β3、β4、β5為各協變量的回歸系數，CORR表示作業相關矩陣，ε表示殘差項，相關代碼見框1，GEE參數估計結果如表2所示。

框1 廣義估計方程代碼呈現Box 1. GEE codes in Python and R

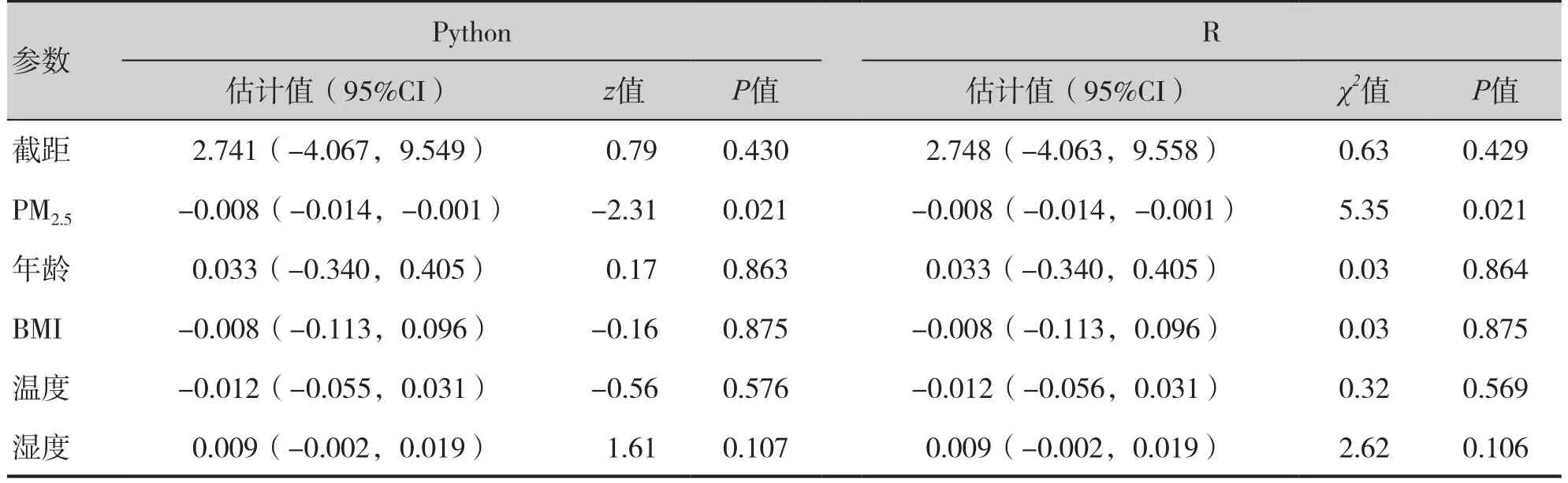
表2 廣義估計方程參數估計結果Table 2. Results of GEE parameter estimation

2.2 MLM建模及參數估計結果

根據MLM定義，可構建如下MLM模型：FEV1 = β0+ β1PM2.5+ β2Age + β3BMI +β4Temperature + β5Humidity + Ζγ + ε

β0為總截距，β1、β2、β3、β4、β5為各協變量的回歸系數，ε為殘差項，Zγ是隨機效應，對應研究對象的個體差異帶來的隨機截距。相關代碼見框2，MLM參數估計結果如表3所示。

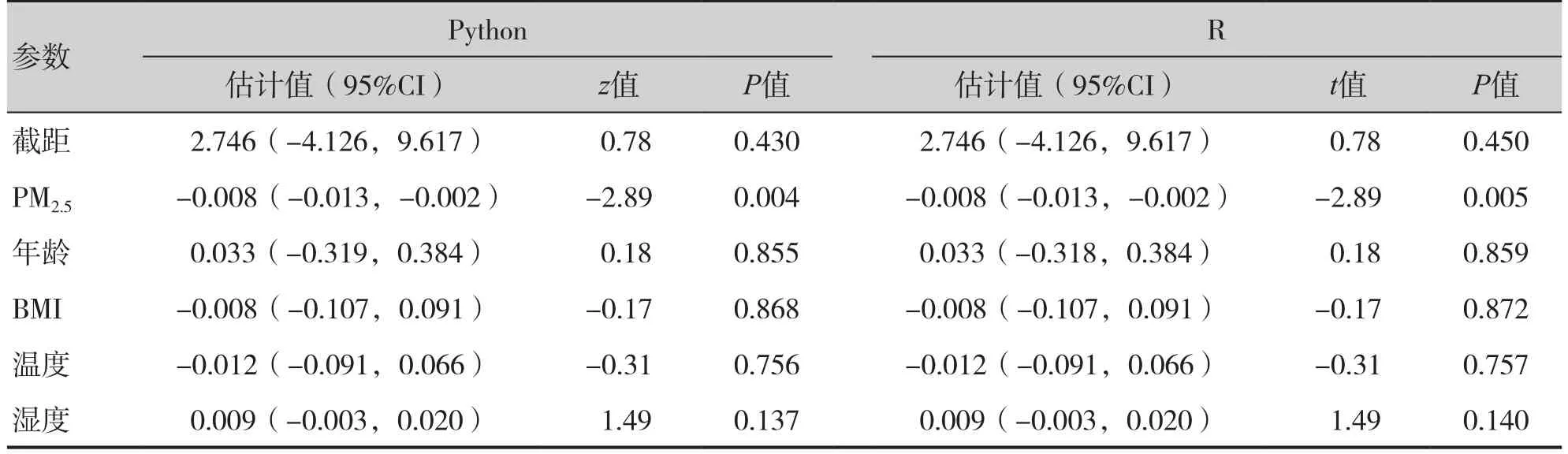
表3 混合線性模型參數估計結果Table 3. Results of MLM parameter estimation

根據模型中自變量的檢驗結果可知，PM2.5是肺功能降低的危險因素，PM2.5每升高1 μg/m3，研究對象2天后的FEV1減少8 mL（P＜0.05）。GEE模型中，Python與R輸出的檢驗統計量分別為z和χ2，同一自變量參數檢驗結果與P值基本一致；MLM模型中，Python與R輸出的檢驗統計量分別為z和t，同一自變量參數檢驗結果與P值基本一致，表示Python輸出結果基本可信。

框2 混合線性模型代碼呈現Box 2. MLM codes in Python and R

3 討論

本文結合流行病學中的研究實例，簡要介紹了GEE和MLM在Python中的具體操作，拓展了縱向數據分析的實現方法。盡管縱向數據在Python與R軟件中的實現代碼有些許不同，但輸出的參數和P值檢驗結果基本一致，反映Python輸出結果可信。在不同的軟件中，相同的方法模型輸出的統計量有所差異，這是開發人員的統計檢驗傾向導致的。鑒于Z統計量值的平方等于Wald χ2統計量的值，因此Wald χ2檢驗是等價于Z檢驗的[16]；在大樣本（n＞50）的情況下，t檢驗與Z檢驗結果也是近似的[17]，所以軟件輸出參數統計量的不同不影響參數檢驗結果。

Python在數據分析方面存在諸多優點，其完善的作圖功能以及豐富的數據分析庫、機器學習庫的發展，越來越符合大數據背景下的數據分析要求。例如，陳偉等使用Python相似度分析與標簽云分析方法進行文本數據分析，拓展了大數據審計的研究方向[18]；楊俊秀等采用Python的matplotlib庫、numpy庫和scikit-learn庫完成了數據的可視化、整理與分析，顯著提高了高頻電子線路實驗數據的處理分析效率[5]。但Python也存在著不足之處，其用作數據分析工具的時間較短，更多的數據分析方法程序有待進一步開發及完善。本研究使用的statsmodels庫目前可實現簡單線性模型、廣義線性模型、GEE、MLM等大部分模型的建模。隨著statsmodels庫的進一步開發，相信未來statsmodels庫可滿足更多的建模需求。

綜上，將Python用于環境流行病學，在實現數據獲取、處理與分析的過程中，統一了語言環境，避免了數據在不同平臺間的轉換，提高了數據分析的效率。使用Python軟件可靈活實現 GEE和MLM的統計建模，在實際研究中有一定參考價值。