基于EHO-FF算法的智能電網無功優化研究

李旭炯，楊郭明，孫林花

(1.蘭州資源環境職業技術大學，甘肅 蘭州 730021； 2.國網蘭州供電公司，甘肅 蘭州 730070)

智能電網優化電力生產、分配和消費，保持電網穩定運行，克服分布式發電的高滲透問題[1]，減少溫室氣體排放，提高電網效率與可靠性，是電力行業發展的新方向[2]。智能電網技術正在從供給側控制的網絡向需求側互動的網絡轉變[3]。在智能電網中實施需求響應優勢明顯，能降低成本和排放、減少燃料依賴、提高系統可靠性等[3]。智能電網面臨的最大挑戰是如何降低系統損耗，改善母線電壓，從而控制供電成本。需求側管理(demand side management，DSM)使用戶可結合具體需要選取不同用電方式，讓用戶通過選擇發電方式和調整需求來獲得更低價的電能[4]，對優化電力資源配置、促進能源利用效率提升等起到重要作用。隨著可變分布式發電單元的持續發展，傳感技術、數據處理、自動控制和通信等領域的先進技術在配電網中的應用越來越廣泛[5]，可再生能源分布式發電已成為智能電網發展新方向。

無功優化可降低電力系統的功率損耗，改善系統的電壓分布[6]。智能電網中的分散無功最優控制是一種先進的電力系統優化控制方法[7]，能降低系統有功損耗，改善電壓分布，但用假設數據降低了結果準確性，增加了問題復雜性[8]。為此提出了各種優化方法，可分為集中式和分布式2類。文獻[9]提出家庭DSM系統，隨著配電系統負荷增加，家庭用電成本也隨之增加。為降低家庭用電成本，提出基于人工神經網絡算法的主動DSM。文獻[10]提出的能源管理系統，通過引入可再生能源降低成本，使消費者參與智能電網技術中。文獻[11]將人工神經網絡與馬爾可夫鏈結合用于不確定負荷需求的最優生成，并將改進人工蜂群算法用于能量管理系統。文獻[12]提出一種基于多目標優化方法的高功能半分散電力匹配框架。文獻[13]提出考慮能量流動和熱交換的互聯智能建筑的最優能源管理，通過功率交換和熱交換增加了蓄熱壽命，降低總運行成本。文獻[14]建立由光伏發電、冷熱電聯合、儲能系統和響應負荷組成的智能園區微電網模型，研究考慮價格需求響應的智能園區微電網機組最優調度策略。文獻[15]提出一種進化模擬優化框架，用于在設備負載不確定的智能電網上實現“容災”策略。文獻[16]提出一種智能電網中用戶損失最小化的解決方案。文獻[17]提出一種基于電力系統微網格的能量管理優化方法。文獻[18]開發一種有效保護隱私的電力用戶控制協議，允許電力企業在不侵犯用戶隱私的情況下控制電網供需。

總結近年研究成果，智能電網中無功優化可降低發電成本。考慮用戶不確定負荷需求、分布式可再生能源和儲能設備的情況下，由能源用戶組成的配電網與電力企業雙向實時通信，對電力系統無功優化。最優方法要使系統成本和損失最小化，同時滿足負荷需求、儲備需求和每個獨立單元的物理和運行約束。但遇到中型或大型問題時，已有方法無法在規定時間內解決問題。

本研究提出以DSM為優化對象，引入象群優化-螢火蟲進化(elephant herd optimization-firefly，EHO-FF)算法，來解決包括等式和不等式約束(供需平衡、母線電壓、線路和無功功率限制等)的優化問題。IEEE30母線系統中，考慮不同場景下的無功最優解，基于最優無功控制方法，改善不同運行條件下電網的能效和電壓分布。

1 智能電網無功優化建模

1.1 智能電網無功優化

圖1為智能電網無功優化(reactive power optimization，RPO)的系統示意圖。采用EHO-FF算法對所研究的系統在不同負載下進行無功優化，目標是已知系統和所有分布式發電(distributed generation，DG)單元母線的現有需求前提下，通過優化DG單元規模使功率損耗最小，并給出物理約束(發電機與松弛母線無功產生的局限性，電容器輸出，變壓器變比)和操作約束(除松弛母線外母線電壓幅值的界限)下最優目標值(DG值、實際功率損耗和電壓偏差)。

1.2 RPO目標函數

RPO目標函數為最小功率損耗Ploss，如式(1)所示。

(1)

式中：Vi為母線i的電壓幅值；Vj為母線j的電壓幅值；Gij為母線i與j之間的電導；θij為母線i與j之間的電壓角；S為母線支路總數。

潮流方程如式(2)—式(4)所示。

(2)

(3)

(4)

無功功率產生的輸出限制，靜態無功補償器的容量限制，電壓幅值的規定范圍(松弛母線除外)及變壓器Tl抽頭位置的限制如式(5)所示。

(5)

RPO變量分為狀態變量(負載母線角度、電壓幅值、發電機母線無功功率、松弛母線實際發電量)與控制變量(發電機母線電壓、并聯電容器/電抗器輸出及變壓器變比)。系統母線順序定為松弛母線、發電機母線和負載母線(帶有并聯電容器/電抗器的負載母線在順序中更靠前)。基于此順序，狀態變量X如式(6)所示。

(6)

控制變量U如式(7)所示。

(7)

由于RPO關注的是無功和電壓分布優化，因此忽略了實際電力線路電流和松弛母線實際發電量等潮流分析中所包含的約束條件。已知有功功率，變壓器與并聯電容器/電抗器變比在實際中是離散變量，引入補償函數可有效解決。

由于RPO輸入中存在不確定因素，使其成為不確定的非線性規劃問題，可表示為模糊數、隨機數和區間。本研究中，由于RPO模型的自驗證計算，因此選取區間來描述不確定性。與有功和無功變化相關的不確定性，比其他類型的不確定性(如輸電線參數的不確定性)更需關注。但文獻[19]只考慮了有功產生和負荷需求的不確定性。為便于理解，發電側有功功率區間如式(8)所示。

(8)

負載側有功功率區間如式(9)所示。

(9)

負載側無功功率區間如式(10)所示。

(10)

在此基礎上，由于發電側母線有功功率和無功功率為確定值。推導帶區間不確定性的平衡方程后，RPO數學模型如下。

minf(X,U)=[fL,fU]

(11)

h(X,U)=[hL,hU]

(12)

min(g)≤g(X,U)≤max(g)

(13)

式中：f(X,U)，h(X,U)，g(X,U)為區間函數；[fL,fU]為實際功率損失區間；[hL,hU]為潮流變化區間。

狀態變量和控制變量X和U分別對應于RPO模型的X和U。由于發電側電壓由勵磁系統確定，因此該模型中U為實值向量，并聯電容器/電抗器輸出和變壓器變比也需調整。與X不同，U是由區間值組成，具有不受控的特點。此外，X由U通過區間潮流方程確定，即每一個U對應一個X。因此采用具有區間不確定性的非線性規劃問題來解決，通過EHO-FF算法求解不確定潮流方程區間，進一步提高精度。

2 EHO-FF算法

由于EHO算法搜索性能較差，因此引入FF算法提高EHO算法的搜索性能。EHO-FF算法通過控制不同負載下的損耗，優化無功功率，其程序簡單，易于實現，計算效率高。

2.1 EHO算法優化

EHO算法是一種基于群搜索最優解的啟發式算法，通過象群同類相識的行動原理來尋求系統最優策略，算法內容包括氏族更新與氏族分離。一般來說，每個氏族中的母系族長都是最年長的，作為優化問題，可將氏族中的母系族長想象為最適合的象個體，大象的放牧行為被設定為氏族更新算子和分離算子。

2.1.1 更新算子

氏族更新中，大象依據母系族長為中心原則進行更新。氏族中每一頭大象的下一個位置都受到母系族長的影響[20]。設每個氏族有j頭大象，象群母系族長位置標記為ci，則象群更新后位置模型如式(14)所示。

(14)

需注意的是，有可能象群中存在多個母系族長，而氏族的更新變化可能只有一個中心，因此母系族長的位置受中心位置的限制，如式(15)—(16)所示。

(15)

(16)

2.1.2 分離算子

經過一段時間后，成年大象會離開原氏族重新建立新氏族[21]。利用EHO分離算子，將適應度最差的大象從氏族中分離出來。求解優化問題時，該分離過程可作為分離算子。為提高EHO算法的可搜索性，假設所有氏族中適應度最差的大象個體都采用分離算子，如式(17)所示。

(17)

2.1.3 精英策略

與其他啟發式算法一樣，精英策略用于關注由于部落更新和分離算子淘汰的大象個體，保證后來的大象比之前更好。首先最優大象個體被保存下來，搜索結束時，最差的大象被保存下來的最優大象替換。通過FF算法改進搜索過程，提出的EHO-FF算法流程圖如圖2所示，主要實現步驟如下。

a.初始化大象種群、設最大迭代次數tmax，用適應度函數計算每個大象個體的適應度值，得到當前最優個體位置。

b.根據式(14)更新種群中每個大象個體的位置，使用式(15)、(16)更新當前最優個體的位置。計算更新之后的每個大象個體的適應度值，評估種群，得到更新后的種群最優和最差的大象個體位置。

c.將上一步得到的結果作為FF算法的初始值，設最大迭代次數kmax。

d.根據設定的種群大小，建立相應數量的螢火蟲，在目標函數自變量的取值范圍內隨機確定每個螢火蟲的位置。

e.對于最大化問題，評估過程中直接將目標作為亮度，對于最小化問題，則對目標值取相反數或倒數。之后再對螢火蟲按照亮度進行排序，以確定當前種群中最優的個體。

f.亮度較低的螢火蟲飛向亮度較高的螢火蟲，亮度最亮的螢火蟲隨機移動。循環執行步驟d-f，直到迭代次數k達到設定的最大迭代次數kmax。

g.使用式(17)更新當前最差個體位置，保留更好的解。判斷迭代次數t是否達到最大迭代次數tmax，若是，則輸出當前最優個體位置及對應的適應度值，否則返回執行步驟b。

2.2 FF算法搜索行為研究進展

FF算法是原始的自然啟發式算法，基于螢火蟲的社會行為來解決連續多目標優化問題[22]，滿足3個假設。

a.所有螢火蟲都是單性的，即一只螢火蟲會被其他螢火蟲吸引；

b.吸引力依賴于亮度大小，即較不明亮的螢火蟲會被較明亮的螢火蟲吸引；

c.將螢火蟲亮度設定為目標函數。

FF算法用來管理濾波元件和降低系統的諧波失真。從系統輸入得到誤差電壓值、誤差變化量及等效輸出，降噪值根據輸出值確定。FF算法存在2個關鍵點，即光強I變化和吸引力β[23]。當光吸收系數γ固定時，光強隨距離r變化如式(18)所示。

I(r)=I0e-γr2

(18)

式中：I0為r=0時的光強。

考慮螢火蟲的吸引力與相鄰螢火蟲看到的光強成正比，對其吸引力描述如式(19)所示。

β(r)=β0e-γr2

(19)

式中：β0為r=0時的吸引力。

任意2只螢火蟲i和j在xi和xj處的距離如式(20)所示。

(20)

式中：xi,d為第i只螢火蟲空間坐標xi的第d個分量；xj,d為第j只螢火蟲空間坐標xj的第d個分量；D為問題維度。

螢火蟲i向比螢火蟲j更有吸引力(更明亮)的另一只螢火蟲移動，如式(21)所示。

(21)

式中：α為隨機參數；k為迭代次數；ψi為高斯分布或均勻分布的隨機數向量。

優化過程取決于螢火蟲亮度和螢火蟲向更亮同類的移動。

3 結果分析

3.1 仿真分析

為驗證智能控制器有效性，采用基準IEEE 30母線系統，拓撲圖如圖3所示。

系統由6臺發電機組和41個支路組成，總負荷為283.4 MW，126.2 Mvar。首先，計算每條線路的電壓、功率損耗、有功功率和無功功率。其次，根據配電網無功損耗降低和電壓增強的理論，采用EHO-FF算法將DG定位在最優位置[24]。最后，利用PSO和Bat等算法驗證其有效性。

表1給出了各種優化算法對不同參數的取值。

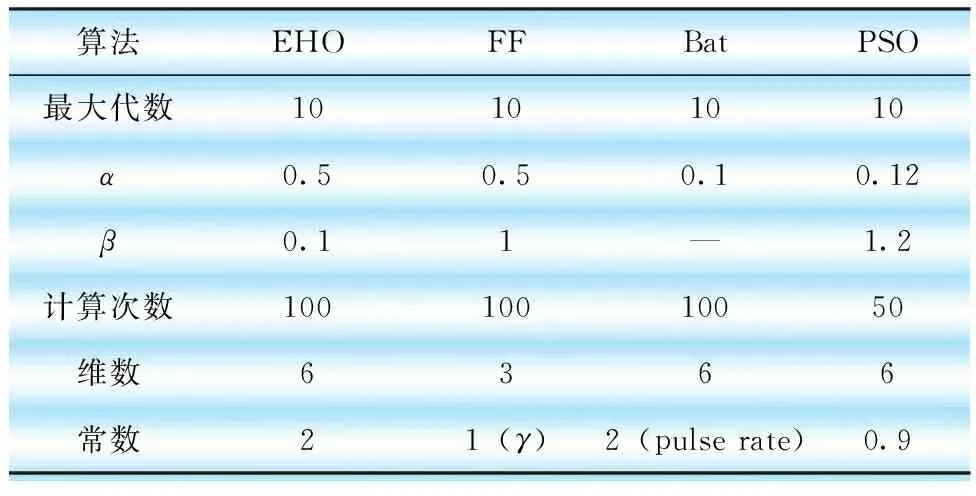
表1 算法參數

考慮一天中隨機變化的24 h負載模式，如圖4所示。首先，用Newton-Raphson法對IEEE 30系統的基本負荷進行程序運行，得到母線電壓幅值、有功功率、無功功率、負載潮流見表2。

表2 Newton-Raphson法求解IEEE 30系統的潮流

從潮流出發，對各支路的電流和損耗進行計算。總有功功率為297.663 MW，無功功率為153.944 Mvar。由表2中得到的發電總負荷和線損結果可知，有功和無功功率均滿足負荷平衡方程。

將DG單元放在發電機母線處(DG1在母線1處，DG2在母線2處，DG3在母線5處，DG4在母線8處，DG5在母線11處，DG6在母線13處)。利用PSO算法獲得不同負載下DG單元的最優規模，如圖3所示。表3給出了利用PSO算法布置與未布置DG時得到的總實際功率損耗。

表3 PSO算法分析隨DG變化負荷需求的功率損耗

采用PSO算法的IEEE 30母線系統在基本負荷下，實際功率損耗和無功功率損耗分別為10.886 MW和43.074 Mvar。布置最佳規模的DG機組后，每個負荷的實際功率損耗和無功功率損耗

如表3所示。無DG時平均實際功率損耗為11.85 MW，有DG時平均實際功率損耗為9.66 MW。因此，在確定位置以適當規模布置DG后，實際功率損耗降低。

同樣，利用Bat算法獲得不同負荷下，PSO算法已考慮過的放置在識別位置的DG單元的最優規模，如圖3所示。通過計算，IEEE 30母線系統在基本負荷條件下的線路損耗為8.556 MW和34.389 Mvar。以最佳規模布置DG單元后，對每個負荷下的功率損耗進行計算，結果如表4所示。無DG時的實際平均功率損耗為11.4592 MW，有DG時的實際平均功率損耗為7.3971 MW。因此，在確定位置以適當規模布置DG后，平均實際功率損耗降低。與PSO算法的結果對比，發現Bat算法在考慮所有負載情況下均能降低實際損耗和無功損耗的平均值。

表4 Bat算法分析不同負荷下隨DG變化的功率損耗

將EHO-FF算法應用于布置有DG的IEEE 30系統，模擬各種負荷下DG單元的最優規模，結果如表5所示。與PSO算法和Bat算法相比，未布置DG的情況下平均功耗降低到11.4592 MW，布置DG后平均功耗降低到7.3971 MW。

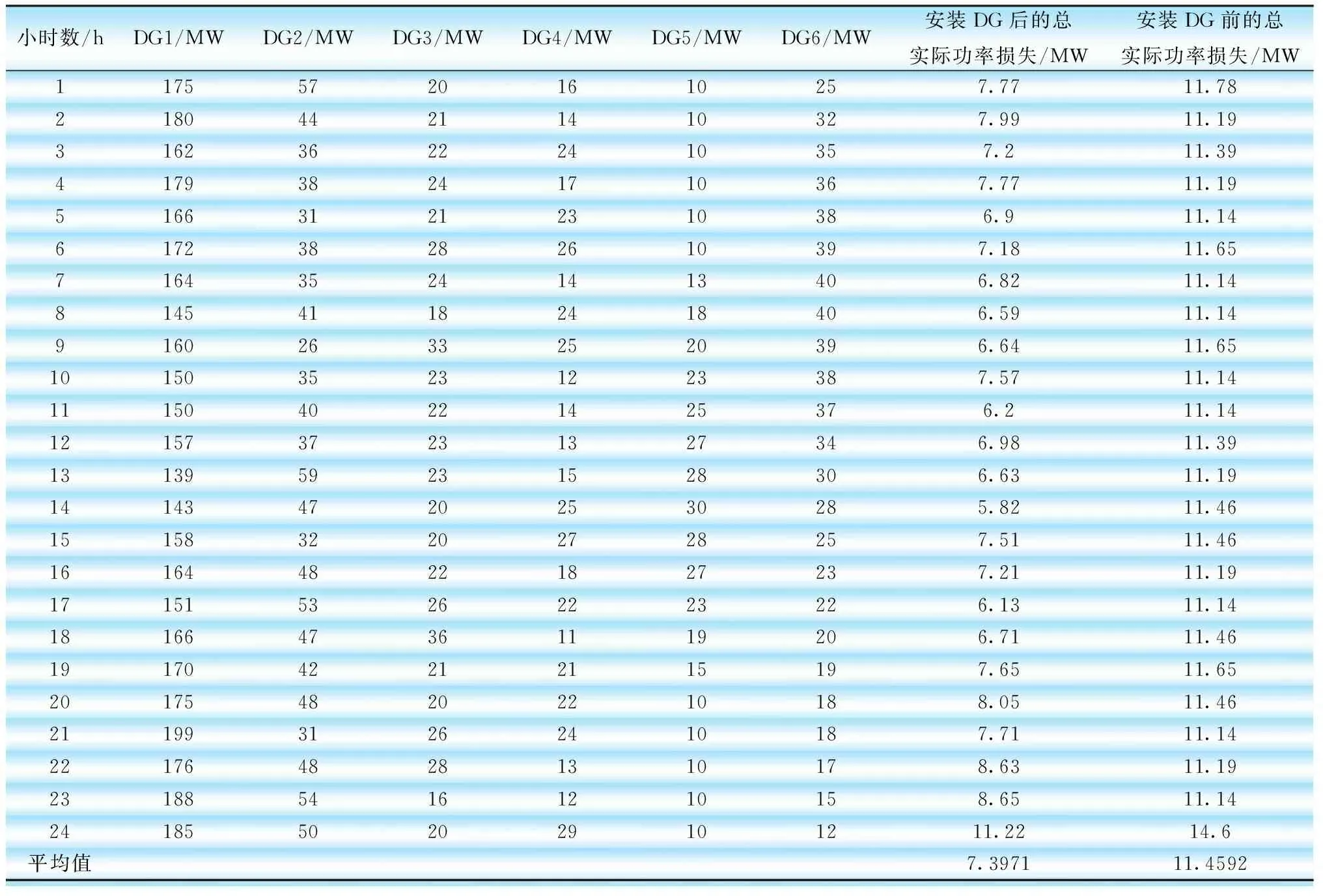
表5 EHO-FF算法分析不同負荷下隨DG變化的功率損耗

PSO算法、Bat算法及EHO-FF算法的收斂性如圖5所示。可以看出，EHO-FF算法與其他算法相比，收斂速度更快，迭代次數最少，能得到最優解。證明所提出EHO-FF算法的有效性和可行性。

3.2 不同算法結果比較

IEEE30系統在未布置與布置DG單元，采用Newton-Raphson、PSO、Bat和EHO-FF算法的結果對比分析如表6所示。基本負載情況下，EHO-FF算法的實際功率損耗和無功功率損耗都是最小的。布置DG單元后與其他算法相比，實際功率損耗也最小。

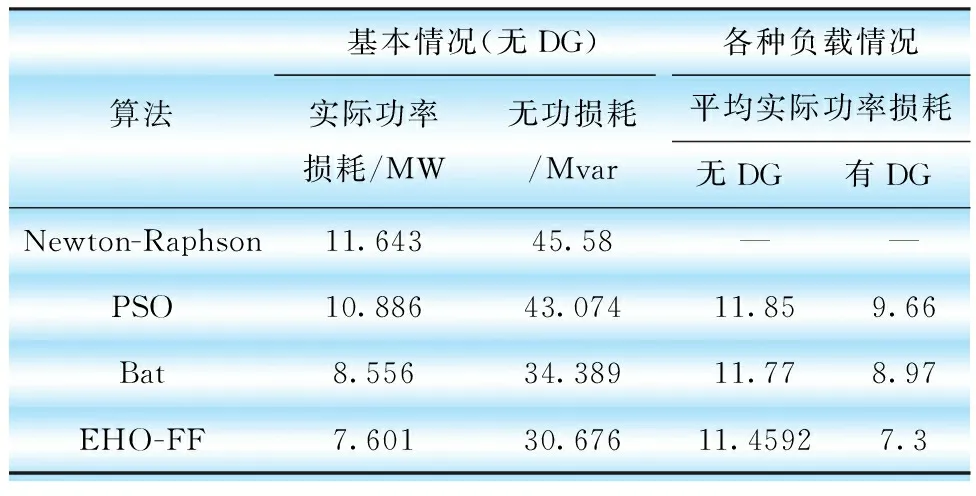
表6 IEEE 30系統未布置與布置DG單元的比較分析

根據各種優化算法的收斂結果，得出系統各母線處的電壓分布。不同算法得到的電壓分布如圖6(a)所示。由圖6(a)可知，與其他算法相比，EHO-FF算法可改善母線的電壓分布，平均電壓分布為1.02 pu。

系統中布置DG時，24 h實際總功率損耗如圖6(b)所示。由圖6(b)可知，采用EHO-FF算法的實際功率損耗明顯降低。由表6可看出，EHO-FF算法的總實際功率損耗平均指標為7.39 MW，與其他算法相比有所降低。

綜上所述，提出的EHO-FF算法優于其他算法，并通過試驗更有效地優化智能電網的無功功率，提高不同電力企業的需求響應。

4 結語

本研究提出了針對智能電網無功優化的EHO-FF算法，將其描述為包含所有約束的優化問題，并與PSO、Bat等算法進行比較。結果表明，所提出的EHO-FF算法能最大限度地降低實際功率損耗，并顯著改善系統的電壓分布，在滿足約束條件和節省時間方面具有優勢。本研究僅涉及智能電網的損耗降低與改善電壓分布，未考慮生產成本、DG成本等。下一步研究方向嘗試由EHO-FF算法來解決包括各種成本函數及其相關約束的優化問題。