偏心量對偏心型漸開線柔性板彈簧性能影響分析

許 信，劉 波，董 皓，張君安

（西安工業大學機電工程學院，陜西 西安 710021）

1 引言

柔性板彈簧（之后簡稱板彈簧）是在彈性金屬片上通過光化學腐蝕等方法加工出不同種類的型線，通過施加軸向力，它可以發生一定的軸向位移，同時也能保證其擁有極大的徑向剛度[1]。課題所研究的用于純電動汽車空調取暖方面的自由活塞自特林熱泵的總體結構圖，如圖1所示。一部分為板彈簧，板彈簧用于支撐動力活塞和配氣活塞，保持運動過程中活塞與氣缸間的密封間隙，板彈簧性能的好壞直接關系到斯特林熱泵的運行平穩性和輸出效率。所以，針對板彈簧的性能研究有著重要的理論價值和工程價值。

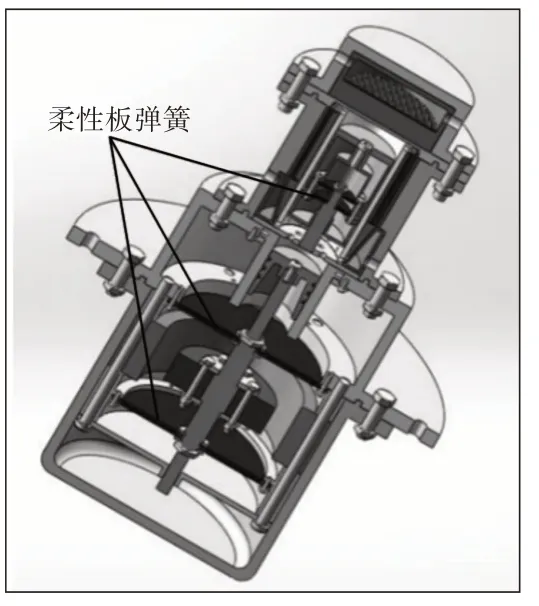
圖1 斯特林熱泵總體結構圖Fig.1 General Structure of Stirling Heat Pump

1981年，文獻[2]首次將板彈簧用于低溫制冷機，使得低溫制冷機的無油潤滑和間隙密封技術成為可能，之后，板彈簧在斯特林機領域獲得了廣泛的關注和應用。文獻[3-4]針對國外柔性板彈簧利用CAD分析的前提下，給出了圓漸開線柔性板彈簧的設計方法，并且更進一步的對柔性板彈簧的性能進行了理論分析。文獻[4]結合有限元分析與實驗結果得到圓漸開線更適用于渦旋線的構造且偏心型漸開線板彈簧具有較優的應力分布等優點。

這里對多種不同偏心量的三槽偏心型漸開線板彈簧建立三維模型，通過推導計算分析了設計偏心型板彈簧時偏心量的取值范圍。通過建立有限元分析模型，應用有限元軟件對不同偏心量的板彈簧的軸向剛度、徑向剛度進行了分析。并對所加工的不同偏心量下的板彈簧進行了軸向剛度實驗。

2 偏心量取值范圍的確定

設計三槽偏心型板彈簧時，需要構造偏心型漸開線，偏心型漸開線發生于三個不同的基圓上，這三個基圓的半徑相同，相鄰兩個基圓圓心與板彈簧中心連線的夾角為120°，連線線段的長度為偏心量。偏心量有一定的取值范圍，當偏心量過大時，會造成兩個渦旋槽相交，使板簧損壞。因此，在偏心型板彈簧設計過程中，需要確定偏心量的最大值，從而得到偏心量的取值范圍。偏心量的取值范圍公式可以根據相鄰兩個渦旋槽之間的最小距離確定。

當相鄰的兩條偏心型漸開線的法線在同一直線上時，這一直線同兩條漸開線交點的連線的長度，即為這兩條漸開線之間的最長或最短距離，如圖2所示。這里只需要求出最短距離公式，即線段EF的長度。根據線段EF的長度，可以求得最終要得到的偏心量的取值范圍。假設長為l，基圓半徑為r，偏心量為x。

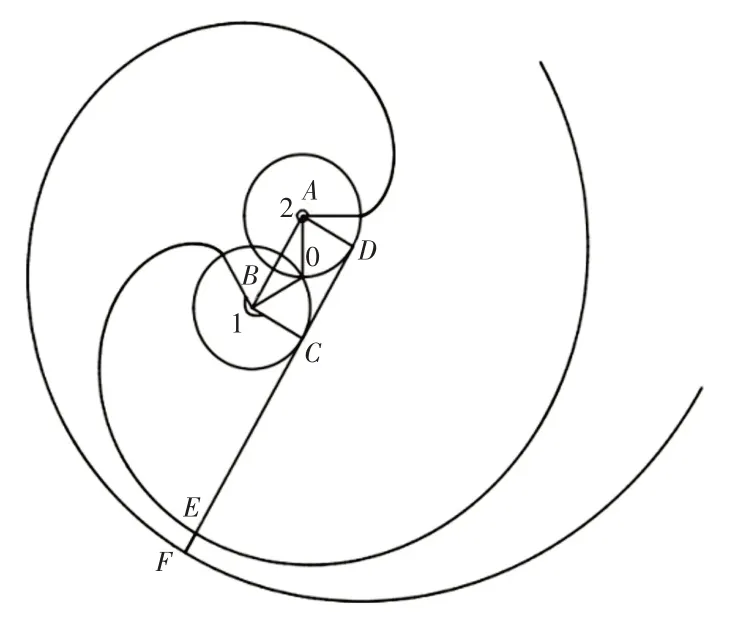
圖2 相鄰兩條偏心型漸開線示意圖Fig.2 Schematic Diagram of Two Adjacent Eccentric Involutes

通過簡單推導，很容易證明四邊形ABCD是一個矩形，從而可以得到：

觀察兩條漸開線的轉角，通過計算推導，可以得到：依據漸開線性質，可以求得以及的長度：

所以，相鄰兩條漸開線之間的最短距離公式：

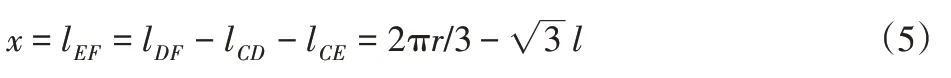
為了保證板彈簧能夠使用，兩條偏心漸開線之間的最小距離應大于0，從而可以求得l＜根據此公式，可以準確的得到偏心量的取值范圍，依據偏心量的取值范圍，在設計偏心型板彈簧時可以節省很多時間。

3 板彈簧設計參數及三維模型

在偏心型板彈簧設計過程中，偏心量的大小對彈簧剛度有明顯的影響。本次研究針對多個不同偏心量，其余參數全部相同的板彈簧進行有限元分析，總結得到徑軸向剛度隨偏心量的變化規律，為偏心型漸開線柔性彈簧設計提供參考依據。除偏心量外，板彈簧設計參數，如表1所示。

表1 板彈簧設計參數Tab.1 Design Parameters of Plate Spring

考慮到斯特林熱泵復雜的工作狀態，要求板彈簧要具備良好的彈性，抗導磁性，耐腐蝕性等要求。又考慮到鈹青銅優越的彈性性能，是銅合金中性能最好的高級彈性材料，具有有色金屬彈性之王之美稱。

最終決定選擇被青銅材料Qbe2作為板彈簧的材料。在板彈簧其余設計參數確定后，根據板彈簧設計參數，通過選取不同的偏心量，利用SOLIDWORKS軟件建立了八種不同偏心量下的板彈簧三維模型，如圖3所示。

圖3 不同偏心量下板彈簧的三維模型Fig.3 Three Dimensional Model of Plate Spring with Different Eccentricity

4 板彈簧徑軸向剛度的有限元分析

對板彈簧徑軸向剛度進行分析時，采用了有限元分析方法[5-6]。有限元法己在有關板彈簧性能研究的諸多文獻中引用，并被證實是一種有效的分析方法。這里采用ANSYS軟件進行分析。

在有限元分析過程中，通過多次改變徑向或軸向施加力，觀察板彈簧的徑向或軸向位移，發現所施加力與位移呈正比關系。分析不同偏心量下各板彈簧的軸向剛度時，在板彈簧中心孔的內表面上對板彈簧施加軸向力，進行求解，觀察不同偏心量下板彈簧的軸向位移云圖，結果，如圖4所示。

圖4 不同偏心量的板彈簧軸向位移云圖Fig.4 Axial Displacement Nephogram of Plate Spring with Different Eccentricity

分析不同偏心量下各板彈簧的徑向剛度時，在板彈簧中心孔的內表面上對板彈簧施加徑向力，進行求解，不同偏心量下板彈簧的徑向位移云圖，如圖5所示。

圖5 不同偏心量的板彈簧徑向位移云圖Fig.5 Radial Displacement Nephogram of Plate Spring with Different Eccentricity

在不同偏心量下板彈簧軸向剛度分析過程中，對每片板彈簧施加相同的軸向力，觀察得到，隨著偏心量的增大，板彈簧的軸向位移呈先減小后增加的趨勢，剛度定義為力與其引起位移的比。所以，板彈簧的軸向剛度是隨著偏心量的增加是呈先變大后變小的規律。

在不同偏心量下板彈簧徑向剛度分析過程中，對每片板彈簧施加相同的徑向力，觀察得到，隨著偏心量的增大，板彈簧的徑向位移同樣呈先減小后增加的趨勢，所以，板彈簧的徑向剛度隨著偏心量的增大同樣呈先變大后變小的規律。

5 板彈簧軸向剛度實驗研究

在自由活塞斯特林熱泵當中，運動件的運動狀態均為直線往復運動，作為往復運動系統的彈性部件，板彈簧的軸向剛度對整個斯特林熱泵系統的運行平穩性有著很重要的作用。板彈簧的軸向剛度實驗方案，如圖6所示。

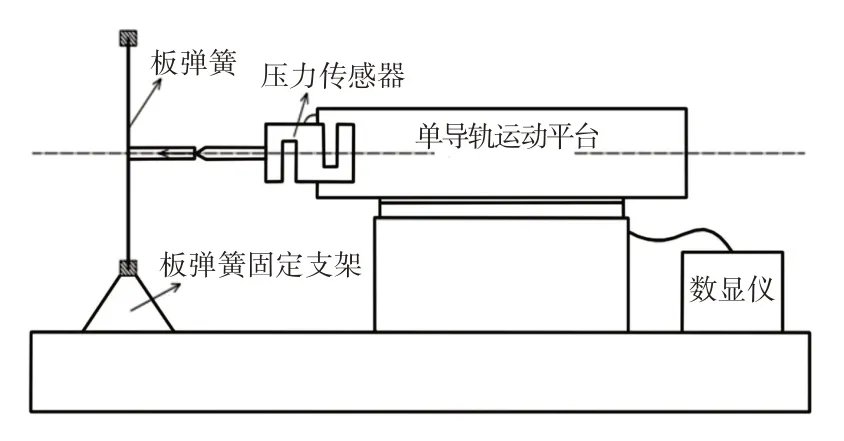
圖6 軸向剛度實驗方案Fig.6 Experimental Scheme of Axial Stiffness

實驗過程中，利用50N量程的壓力傳感器（DYLY-102）以及配套XSB2系列數顯儀表對加工出來的八種偏心量下的板彈簧進行了軸向剛度測量[7-8]，測量裝置，如圖7所示。

圖7 軸向剛度測量裝置Fig.7 Axial Stiffness Measuring Device

板彈簧通過板彈簧支架固定在實驗臺上。板彈簧中心孔處為一螺栓，通過螺母固定，螺桿與壓力傳感器相接觸。力的測量精度為0.001N，軸向進給精度為0.05mm。針對每片板彈簧，每旋轉90°測量3組數據，共測量12組數據，最后選取12組數據的平均值。

給出了偏心量分別為1mm和2mm板彈簧的軸向力與軸向位移的實驗結果關系曲線，兩者變化規律一致，并與有限元分析結果做了比較，如圖8所示。

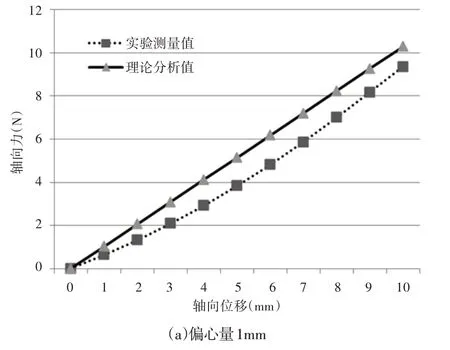
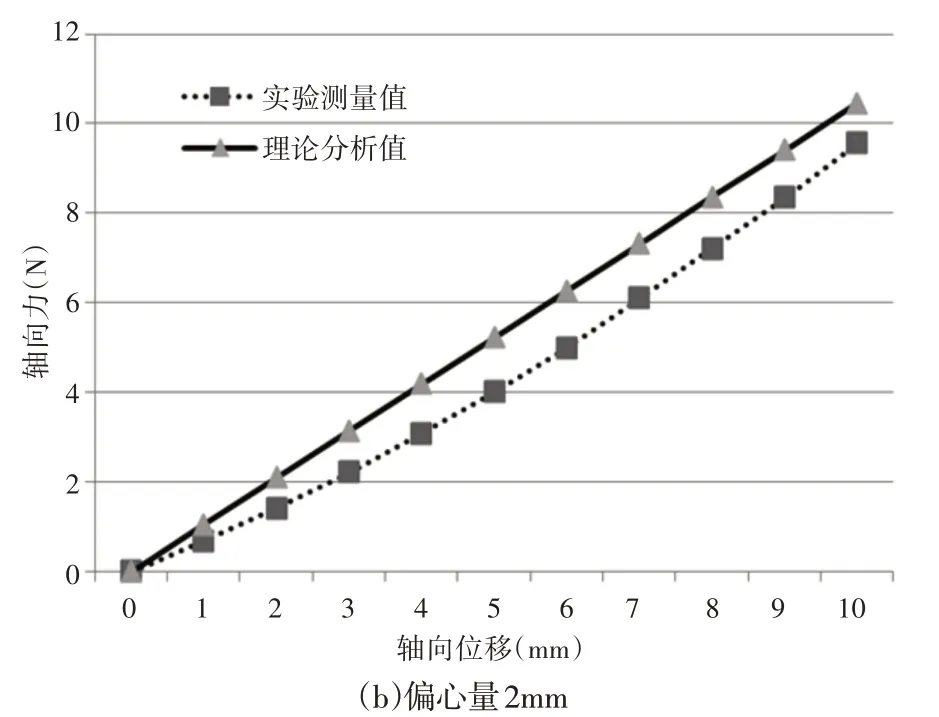
圖8 軸向力與軸向位移關系Fig.8 The Relationship Between Axial Force and Axial Displacement

可以看出實驗值與計算值整體變化趨勢基本相同，但相比計算值較小，且在位移較小時軸向力變化較慢，剛度較小，當軸向位移相同時，軸向力的實驗測量值與理論分析值差值最大在1N左右。

分析原因為在位移比較小時，由于板彈簧與力傳感器之間接觸不充分，導致力隨位移變化較慢，從而彈簧剛度較小。

給出了八種偏心量下的板彈簧的軸向剛度隨偏心量的變化規律，并與有限元分析結果進行了對比，如圖9所示。由對比結果可以看出，實驗值與分析值當中軸向剛度隨偏心量變化的整體趨勢相同，但實驗值偏小，且偏心量在2.5mm之前，軸向剛度的實驗測量值與理論分析值差值維持在0.1N/mm，偏心量在2.5mm之后，軸向剛度下降速度明顯增快，實驗測量值與理論分析值差值變大。分析原因為由于加工誤差，使板彈簧渦旋槽實際寬度比設計值偏大，導致整體剛度較計算值偏小；當偏心量大于2.5mm時，板彈簧軸向剛度對渦旋槽寬度的敏感程度增加，導致軸向剛度下降速度明顯增快。

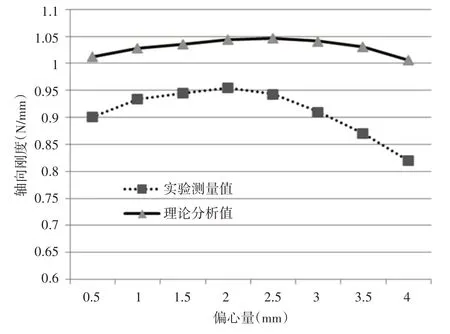
圖9 軸向剛度隨偏心量變化規律Fig.9 The Change Rule of Axial Stiffness with Eccentricity

6 結論

通過對偏心型漸開線以及不同偏心量下偏心型板彈簧徑軸向剛度進行分析，結合有限元結果，歸納出以下結論：

（1）得到了偏心量的取值范圍公式，利用這個公式，可以更加精確地指導偏心型板彈簧的設計工作。

（2）板彈簧的徑向和軸向剛度都是隨著偏心量的增加是呈先變大后變小的規律。

（3）對所加工的不同偏心量下的板彈簧進行了軸向剛度實驗，實驗值與理論分析結果能夠較好的吻合，表明了理論計算值的準確性。