多傳感器融合狀態估計方法綜述

張康皓，董希旺，于江龍，化永朝，任 章

(北京航空航天大學自動化科學與電氣工程學院，北京 100083)

0 引言

物體的狀態，通常指一組可以描述其隨時間變化的物理量，例如位置、速度、加速度以及角度等。狀態估計問題擁有很長的歷史，早在幾千年前，航海家就面臨對船只在海洋中的位置進行估計的問題，這些需求激勵了測量技術的發展。

狀態估計理論的起源可以追溯至1654年帕斯卡和費馬奠定了概率論的基礎，以及1764年貝葉斯法則的提出。1801年，高斯利用最小化觀測誤差提出了最小二乘法，成功估計出了谷神星的軌道，并于1803年證明了在觀測噪聲為正態分布的條件下，最小二乘估計就是最優估計。到20世紀中期，卡爾曼1960年發表的文章為狀態估計理論的發展指明了方向，這種針對高斯線性系統的經典狀態估計方法就是卡爾曼濾波，可以證明，卡爾曼濾波是對高斯線性系統的最優線性無偏估計。基于卡爾曼濾波的思想，通過引入線性化手段，適用于非線性系統高斯噪聲下的擴展卡爾曼濾波(Extended Kalman Filter，EKF)、無跡卡爾曼濾波(Unscented Kalman Filter，UKF)和容積卡爾曼濾波(Cubature Kalman Filter，CKF)算法被陸續提出。此外，20世紀后期提出的粒子濾波、最大后驗估計、貝葉斯估計等狀態估計方法，將狀態估計的應用領域擴展至了非線性系統。

上述狀態估計方法均建立在一對一觀測模型的基礎上，即單個傳感器對單一目標進行狀態估計，而這樣的結構雖然能實現對動態目標的最優或次優估計，但抗干擾能力不強，魯棒性較差；于是，使用多個傳感器對同一目標進行融合狀態估計的思路開始受到研究人員的關注，這就是多傳感器融合狀態估計研究的起點。2004年之前，多傳感器分布式狀態估計的研究處于起步期；得益于網絡一致性算法這一強有力工具的提出，分布式狀態估計得到了蓬勃發展。本文依照由集中式到分散式再到分布式狀態估計的發展順序，對分布式狀態估計的發展進行梳理。

第1章介紹了集中式狀態估計方法。在以高斯線性系統為研究對象時，卡爾曼濾波是最小均方誤差準則下的最優估計(對于非線性系統，可在濾波層面使用EKF、CKF、粒子濾波等非線性濾波方法，不影響集中式狀態估計的架構)。因此，第1章詳細總結了基于觀測融合的集中式卡爾曼濾波方法，作為全局最優的比較基準。

第2章以多傳感器數據融合中的相關數據的融合問題為焦點，總結了由集中式到分散式與分布式狀態估計發展過程中的經典方法。

第3章總結了一致性算法出現后的分布式狀態估計方法，主要有估計一致性、測量一致性和信息一致性等方法，并討論了這些方法的最優性和分布式水平。此外，指出了信息一致性方法分布式地實現了第2章中狀態向量融合的無偏保守估計。

1 集中式狀態估計

本章首先介紹了多傳感器融合狀態估計中最早提出且最直接的思路，即集中式狀態估計方法。在高斯線性系統的最小均方誤差準則下，使用集中式卡爾曼濾波得到融合狀態估計結果，是分布式狀態估計的精度上限和比較基準。

引言中提到，單一傳感器向多傳感器狀態估計推廣能夠提升狀態估計精度，增強系統的魯棒性。較為直觀的思路是，收集多個傳感器對目標的觀測，集中執行狀態估計。麻省理工大學的D.Willner等在1976年的文章中提出了適用于多傳感器系統的卡爾曼濾波算法，將多個傳感器的觀測合成為一個向量再進行卡爾曼濾波，可實現全局最小均方誤差估計，這種方法也因此被稱作集中式卡爾曼濾波。設個傳感器對系統狀態隨機向量的觀測方程為

+1,=(+1)++1,

(1)

若所有傳感器的觀測數據被同步收集，則有

(2)

在傳感器觀測噪聲互不相關的條件下，觀測向量的協方差矩陣為

(3)

至此，基于觀測融合，D.Willner等提出了三種濾波方法。當系統為線性高斯且傳感器同構的情況下，三種方法等價，均為最優估計，第一種方法運算量最大，第三種最小。

1)并行濾波器：這種方法在收集觀測數據的中心節點時直接采用卡爾曼濾波對狀態向量進行求解，但矩陣維數隨傳感器數量而增加，導致直接求解計算負荷較大。

2)順序濾波器：順序結構的濾波器將收集到的個傳感器的觀測數據依次用于卡爾曼濾波的更新中，即下一時刻全局的狀態更新需要進行次卡爾曼濾波。

3)數據壓縮濾波器：所謂數據壓縮，是指對個觀測向量進行融合后再進行卡爾曼濾波，事實上，這種方法利用了最優加權最小二乘估計對觀測向量進行融合

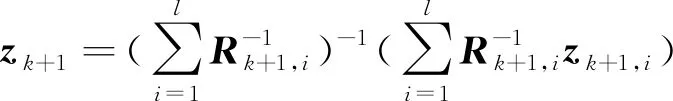
(4)

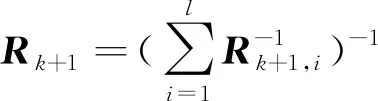
(5)

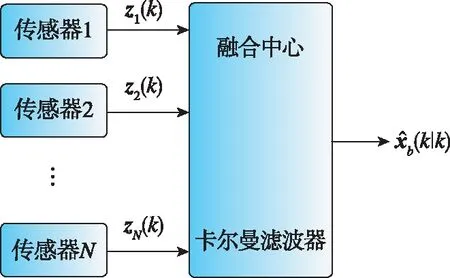
得到了壓縮的觀測向量及相應的協方差矩陣后再進行卡爾曼濾波，但在傳感器異構時不可用。在圖1所示的集中式融合狀態估計架構中，數據關聯和時空配準是多傳感器融合中的必要步驟，濾波算法在融合中心進行實現。

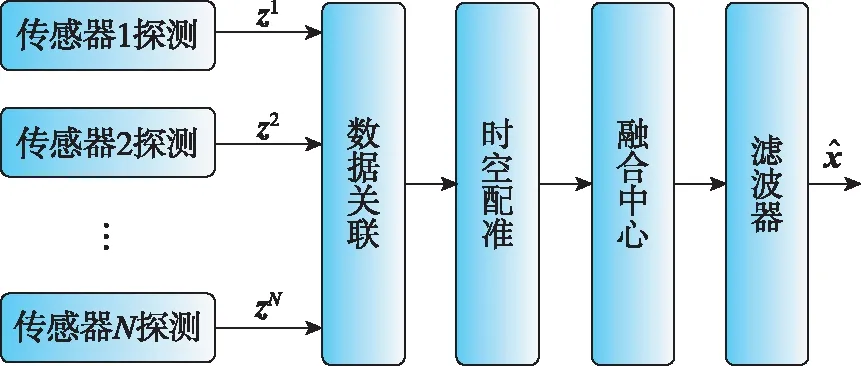
圖1 集中式融合狀態估計架構Fig.1 Centralized state estimation structure

由于均需要收集所有傳感器的觀測，以上三種方法也被稱為觀測融合(measurement fusion)。這些方法要求每個傳感器與中心節點進行通信，對計算量、存儲能力以及通信能力的要求較高，并且容錯能力較弱。因此，若在每個傳感器執行本地估計，利用信息融合的方法實現分布式融合狀態估計，可克服集中式狀態估計的不足。分布式狀態估計開始成為新的研究熱點。

需要注意的是，對于高斯線性系統，集中式卡爾曼濾波是最小均方誤差意義下的全局最優估計。可以證明，卡爾曼濾波給出的誤差協方差矩陣位于克拉美羅下界處，所以卡爾曼濾波是最優線性無偏估計(Best Linear Unbiased Estimate，BLUE)。因此，集中式卡爾曼濾波是所有線性無偏狀態估計方法中誤差比較的基準，分布式方法的估計精度不能超越集中式。

2 多傳感器數據融合——相關數據的融合方法

在多傳感器分布式狀態估計的研究進程中，對來自不同傳感器的數據進行融合及利用是最基礎的問題，而分布式則主要關心如何將融合方法在傳感器網絡中的每個節點本地實現。2013年，B.Khaleghi等給出了關于多傳感器數據融合(Multi Sensor Data Fusion，MSDF)技術的全面回顧，總結了MSDF面臨的挑戰及其應對方法，包括數據缺陷、數據相關性、數據不一致性等問題，如圖2所示。其中，數據相關性問題伴隨著MSDF的發展，是最受研究者關切的問題之一。本章聚焦多傳感器數據融合中的數據相關性問題，并將在之后的章節中展示分布式狀態估計算法是如何解決這一問題的。

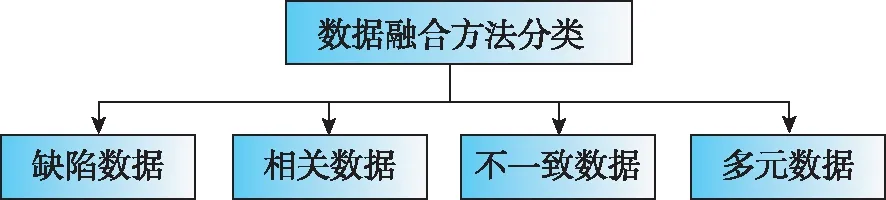
圖2 數據融合方法分類Fig.2 Taxonomy of data fusion methods

2.1 有相關性數據的融合——狀態向量融合

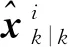
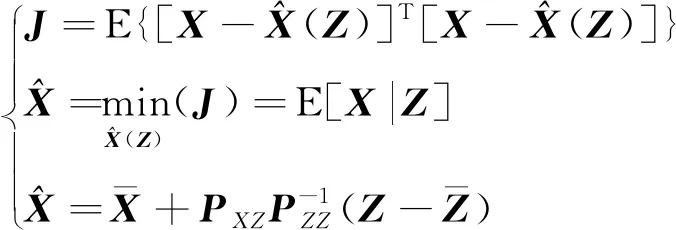
(6)

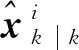
(7)

其中，、分別為傳感器的估計誤差方差矩陣和傳感器、估計誤差之間的交叉協方差矩陣。上述融合結果可以寫為如下形式

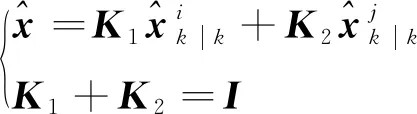
(8)

綜上所述，這種狀態向量融合的方法可以在已知估計誤差相關性的情況下，以最小均方差為準則融合兩個傳感器的狀態估計。文獻[9]通過仿真實驗對比了第1章介紹的集中式卡爾曼濾波的觀測融合與上述狀態向量融合方法的性能表現，說明了狀態向量融合方法的估計誤差始終高于集中式的觀測融合方法。因此，這種狀態向量融合方法并不是最優的，而被證明是一種次優估計，相比集中式狀態估計，其優勢在于更低的計算負荷以及可被用于分布式結構的狀態估計。由于觀測融合與狀態向量融合方法均受卡爾曼濾波思想的啟發，在后續的研究中，這兩種狀態向量融合方法也被歸為KF(Kalman Filter)融合方法。

2004年，S.L.Sun等基于矩陣加權線性最小融合方差，推導出了在這一準則下的多傳感器最優信息融合方法，可看作是Bar-Shalom/Campo公式在多傳感器數據融合下的推廣。假設對同一個維隨機向量有個無偏估計

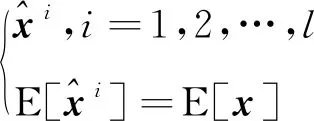
(9)

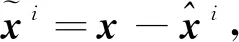
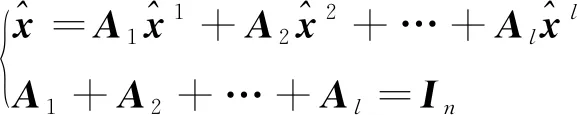
(10)

為待定系數矩陣的最優無偏融合估計，根據無偏估計的性質，加權矩陣的和等于單位矩陣。則融合后的誤差協方差矩陣為

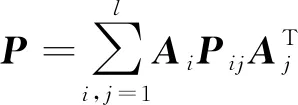
(11)

為了最小化式(11)所示的誤差協方差矩陣的跡，本文通過拉格朗日乘子法給出了最優加權矩陣以及相應的誤差協方差矩陣

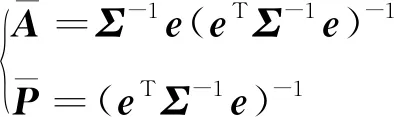
(12)

其中，=[,…，],=()×。事實上，Sun等對多傳感器加權融合后的誤差協方差矩陣的跡進行的最小化方法，與Y.Bar-Shalom等對兩個傳感器采用的卡爾曼濾波融合方法等價，這是由于式(6)所示的估計誤差方差與式(11)中誤差協方差矩陣的跡是相同的。

Sun等由此提出了分布式傳感器信息融合的雙層融合結構，第一層用于計算任意兩個傳感器估計誤差之間的協方差矩陣，第二層進行權重的計算與數據融合。也就是說，這種方法需要每個傳感器能夠對網絡中的其他傳感器進行點對點廣播通信；并且需要獲取每個傳感器間的相關性，通信量和運算量隨著傳感器數量的增加而呈指數增長，可擴展性不強。

(|)=(|,)

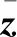
(13)

這意味著?,其中，和分別是傳感器與傳感器的累積觀測數據，顯然該假設是不合理的。同時，Chang K.C.等還指出，這種狀態向量融合方法是缺少先驗信息時的最大似然估計，因此是一種次優估計。

此外，Chang K.C.等還分析了Chong C.Y.于1979年提出的一種層次估計方法，也被稱為基于信息融合的方法能夠做到分布式的全局最優估計，其具體形式如下

(14)

表1 幾種多傳感器數據融合方法比較

綜上所述，本文介紹的對于線性高斯系統的多傳感器融合方法中，集中式的觀測融合方法1)可以實現全局的線性最小方差估計，是一種最優估計，但矩陣維數高，計算量大；觀測融合方法2)、3)在傳感器同構時與方法1)等價，并且能夠降低計算量。狀態向量融合方法是一種次優無偏估計，實現了多個傳感器狀態估計向量加權時的最小方差，被文獻[10]證明是最大似然意義下的最優，并非全局最小均方差；但這種方法計算量小，可實現分布式的融合架構。此外，還有學者對狀態向量融合進行了改進，將融合后的狀態估計用于下一時刻所有傳感器的預測步，而不再用各自傳感器融合前的狀態估計，在異構傳感器網絡中取得了更好的表現。信息融合方法采用所有傳感器的先驗信息及狀態估計信息，在高速率通信時可以實現最優估計，從融合形式上看，也是一種廣義的狀態向量融合(狀態估計向量及其先驗)；但該方法通信量大，計算量大，通信實時度下降時將退化為次優估計。此外，N.A.Carlson提出的聯邦濾波器也是多傳感器融合狀態估計中重要的學術貢獻，通過將狀態向量劃分為公共狀態和專有狀態，能夠解決異質傳感器網絡下的融合狀態估計，在大類上也是一種狀態向量融合方法。以上算法可被總結為如下三種融合架構，如圖3所示。

(a) 并行濾波

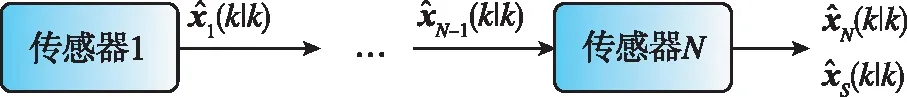
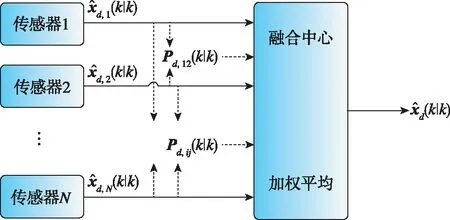
(c) 狀態向量融合圖3 三種不同的傳感器融合架構Fig.3 Illustration of different fusion architectures

圖3(a)所示架構對應于觀測融合方法中的并行濾波器和數據壓縮濾波器。圖3(b)所示架構對應于觀測融合方法中的順序濾波器。圖3(c)所示架構為狀態向量融合方法的示意圖，傳感器進行本地狀態估計后，需要計算兩兩之間的估計誤差協方差矩陣，再進行融合，數據融合可以在中心節點實現，也可以通過傳感器網絡的廣播式通信在所有傳感器本地實現。由于式(14)中的信息融合方法和聯邦濾波器本質上也是一種狀態向量融合方法，因此也可以由圖3(c)中的架構描述。

2.2 未知相關性數據的融合——保守估計

由2.1節的討論可知，傳感器數據融合時需要獲得所有傳感器估計誤差兩兩之間的相關性矩陣。但在實際的傳感器網絡中，由于通信帶來的信息混合、相同的過程噪聲以及傳感器之間可能的位置關聯，傳感器間的估計誤差的相關性是難以避免且通常是難以獲得的，因此，表1提出的融合方法不易完美實現。對于高斯的未知誤差間相關性的情況，S.J.Julier等于1997年提出了協方差交叉(Covariance Intersection，CI)算法，給出了未知傳感器間誤差相關性時線性無偏融合估計誤差協方差的最小上界，CI融合公式如下

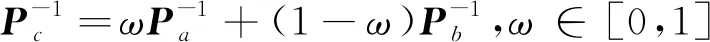
(15)

其中，是使得融合后協方差矩陣跡最小的常數，CI算法給出的融合誤差協方差矩陣是對傳感器間任意誤差相關性的最小上界。Chen L.等對CI算法進行了更直觀的解讀，提出了利用協方差橢圓對誤差協方差矩陣進行可視化的方法。如圖4所示，藍色橢圓為兩個傳感器的估計誤差；綠色橢圓為當兩個傳感器估計誤差間不相關時的融合協方差，即當≠時，式(11)中的=0；黑色橢圓為當傳感器估計誤差間相關性已知(取不同值)時的融合協方差；紫色虛線橢圓為當傳感器間誤差相關性未知的條件下，式(15)中的取不同值時的CI融合誤差。文獻[16]證明了兩傳感器在任意相關性時，融合誤差橢圓均在藍色的估計誤差橢圓相交區域內。可以看出，CI給出的融合估計能對兩個傳感器協方差橢圓相交區域實現緊約束，因此，CI也被稱作保守(Conservative)估計。

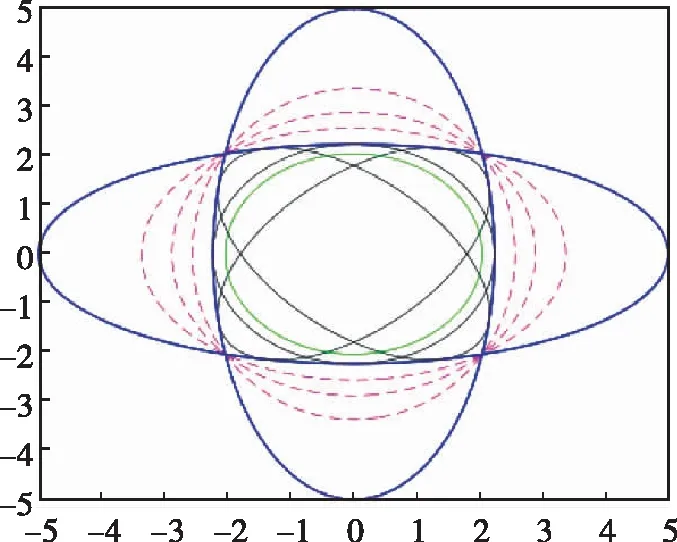
圖4 已知相關性與未知相關性時的傳感器融合誤差橢圓Fig.4 The ellipses for multisensor fusion under known and unknown cross-covariance matrices

CI算法對于融合上界的計算是最優的，并且被M.B.Hurley用信息理論證明可適用于任意的概率分布函數。但文獻[14]也指出，CI算法對于兩個以上的傳感器融合時給出的誤差協方差大于相交區域的緊約束，即CI算法對兩個以上的未知相關性的多傳感器融合結果不再是最小誤差上界。并且CI算法本身也存在著優化計算量大、估計結果悲觀保守等問題。為此，一些快速計算CI的方法以及被稱為最大橢圓(Largest ellipsoid)算法的樂觀估計方法被提出，但這種樂觀估計方法也被證明存在估計缺陷。

總而言之，盡管CI算法不完美，但作為一種處理數據未知相關性的開創性經典方法，具有重要的理論與應用價值。目前，CI仍然是未知誤差相關性時多傳感器數據融合中的首選方法。T.Bailey等還將保守估計思想推廣至了未知的非高斯相關性的情況中。如今，能夠解決未知誤差相關性的保守融合估計方法已經在分布式狀態估計的研究中被廣泛地提出。

3 一致性與分布式狀態估計

早期對多傳感器融合狀態估計的研究與文獻[8]中類似，若要實現分布式狀態估計，一個傳感器節點需要獲得網絡中其他所有節點的信息，即所有傳感器節點需要具備廣播式的全局通信能力；亦或是像文獻[13]中提出的算法，需要一個中心節點進行融合，如圖2所示。正如文獻[30]所述，這些方法只能被稱作分散式(decentralized)狀態估計，而非分布式(distributed)狀態估計。一致性算法與代數圖論的發展使得多傳感器分布式狀態估計架構成為可能。

3.1 一致性算法

在連通拓撲網絡中，僅利用各個節點及其鄰居的通信迭代實現網絡中所有節點的信息或狀態的一致被稱為一致性問題。2004年，加州理工大學的R.Olfati-Saber等解決了切換拓撲與延時網絡的一致性問題(Consensus Problem)，其核心公式為

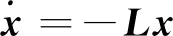
(16)

其中，為網絡的拉普拉斯矩陣；為系統的狀態。Xiao L.等基于矩陣分析，于同年提出了計算平均一致性的快速線性迭代算法以及兩種常用的加權方法：最大度加權和Metropolis加權方法，極大地方便了傳感器網絡對一致性方法的應用。核心公式為

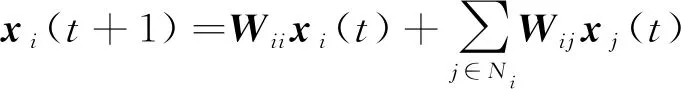
(17)

D.P.Spanos 等證明了Xiao L.等在文獻[32]中由矩陣理論導出的離散一致性算法，可由R.Olfati-Saber等在文獻[31]中基于拉普拉斯矩陣的連續一致性思想推導而來，均可在迭代的穩態分布式地實現各個節點初始狀態的平均一致性，即

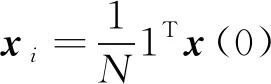
(18)

在傳感器網絡的通信拓撲聯通條件下，平均一致性算法總能使各節點狀態趨于一致，并且收斂于各個節點初始狀態的平均值。一致性算法為分布式狀態估計提供了強大的工具；拓撲網絡能夠僅利用節點與鄰居的通信實現某種信息的一致性，解決了早期多傳感器融合狀態估計研究中對廣播式通信或中心節點的依賴，可以使每個傳感器分布式地得到相同的融合結果。

3.2 分布式狀態估計算法

在隨后的2005年，Xiao L.等將平均一致性方法成功地應用于分布式傳感器融合中，這是一種對觀測對象狀態為非隨機觀測量的分布式最大似然估計。同樣在2005年，R.Olfati-Saber等在文獻[31]的基礎上提出了一致性濾波器，利用現代控制理論論證了這是一種低通濾波器并證明了其穩定性。基于這種一致性濾波器，R.Olfati-Saber等提出的分布式卡爾曼濾波器是首個可擴展且完全分布式的濾波器，由低通一致性濾波器和帶通一致性濾波器組成的微小嵌入式卡爾曼濾波器計算平均觀測和平均逆協方差矩陣，理論上可以實現與集中式濾波相當的估計精度。然而，這種方法的缺陷在于，需要每個傳感器擁有網絡中節點總個數這一全局信息，并且只能應對所有傳感器的觀測矩陣都相同的場景，這是由其使用的低通濾波器的性質所決定的。

2007年，R.Olfati-Saber等對一致性方法進行了全面而詳細的總結，提供了網絡一致性問題的理論框架和邏輯梳理，為后續多傳感器分布式融合估計、協同控制和多智能體系統的發展奠定了堅實的基礎。同年，R.Olfati-Saber等使用高通一致性濾波器對其在文獻[36]中提出的分布式濾波方法進行了改進，使其能適用于不同的傳感器觀測矩陣條件。此外，文獻[38]還基于對傳感器狀態估計結果的一致性運算提出了兩種分布式算法，被稱為CE(Consen-sus on Estimates)算法。同為CE算法的還有F.S.Cattivelli等提出的濾波策略。2009年，R.Olfati-Saber從最優估計角度出發，證明了以CE思想為基礎的算法是一種次優估計。

對于分散式架構的最優估計，早在1988年，H.R.Hashemipour等就基于卡爾曼濾波的信息形式提出了一種計算方法，但由于需要所有節點的信息，無法分布式工作。2008年，M.Kamgarpour等基于卡爾曼濾波的信息形式以及文獻[31-32]中的一致性算法，提出了一種分布式一致性卡爾曼濾波器，并證明了其收斂性。這種方法基于卡爾曼濾波的信息形式為

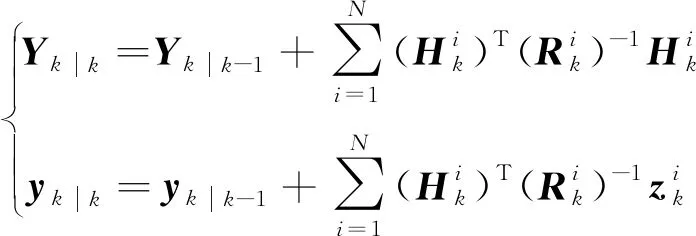
(19)

利用一致性算法，在傳感器網絡各個節點計算信息矩陣增量和信息向量增量的平均值

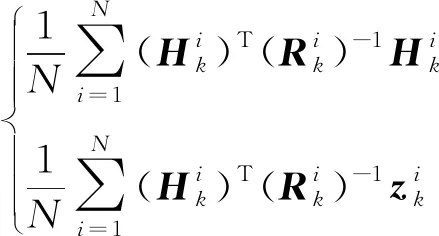
(20)

再用平均值乘以傳感器總數，就可以得到信息矩陣與信息向量的更新值，進而計算狀態估計結果。由于從集中式卡爾曼濾波的信息形式推導得到，這種濾波器理論上具有與集中式濾波相同的估計精度，是一種最優估計，但需要每個傳感器擁有傳感器總數這一全局信息，與算法類似。在G.Battistelli等的研究中被稱為CM(Consensus on Mesurements)算法。

2011年，G.Battistelli等提出了一種被稱為信息一致性(Consensus on Information)的融合算法，該方法的出發點是利用KL散度量化兩個概率密度函數之間的距離，即

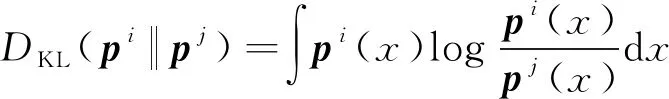
(21)

對于個傳感器的后驗概率密度，再通過求解一個使平均KL散度最低的概率密度函數，得到融合后的概率密度

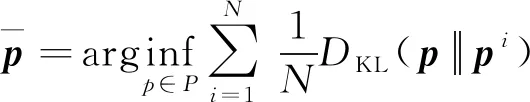
(22)

其計算結果是個概率密度的幾何平均值，對兩個概率密度函數而言，該結果正是文獻[17]中定義的廣義協方差交叉融合(Generalized Covariance Intersection，GCI)，以及文獻[47]中討論的廣義Chernoff信息融合

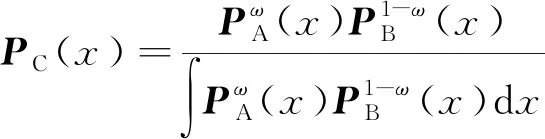
(23)

特別是在高斯概率密度時，式(22)的優化結果具有如下形式

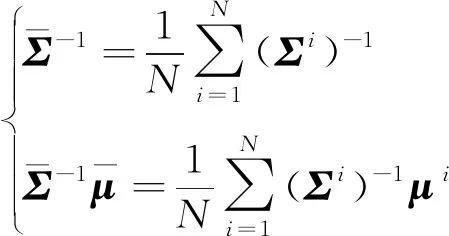
(24)

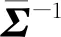
表2總結了本文介紹的自2004年以來的幾種經典的多傳感器分布式融合方法。此外，近年來還有很多研究著力于解決分布式狀態估計中的其他問題，例如非線性、容錯、異質傳感器、數據不一致、信息沖突等問題，本文不詳細解讀。

表2 幾種基于一致性的多傳感器分布式融合方法

4 結論

本文按照由集中式到分散式再到分布式狀態估計的發展順序，簡要梳理了多傳感器融合狀態估計的發展。從直觀的集中式濾波開始，以數據相關性問題為背景，調研了分散式、分布式濾波架構的發展歷程，其中著重討論了數據相關性在傳感器數據融合中的重要性以及相應的已知相關性、未知相關性時的傳感器數據融合方法(保守估計)。早期的研究需要融合中心或節點間的廣播式全局通信能力，屬于集中式或分散式濾波架構，如聯邦濾波器等。隨著2004年一致性問題的解決，大量經典、有效的分布式狀態估計方法被提出，這些方法具備集中式所沒有的魯棒性、抗干擾能力、可靠性以及可擴展性，并且消耗更低的計算和通信資源。最后，本文介紹了一致性算法和一些經典的分布式方法，并在3.2節的末尾指出了信息一致性方法分布式地實現了狀態向量融合的保守估計。對集中式、分散式和分布式狀態估計方法的特點及其之間的聯系總結如下：

1)集中式濾波架構：并行濾波、順序濾波、數據壓縮濾波。

以上三種集中式濾波方法也被稱為觀測融合，需要中心節點且需要所有傳感器的觀測值，三種方法在線性高斯系統且傳感器同構時等價。

2)分散式濾波架構：狀態向量融合、聯邦濾波、信息融合。

以上三種基于分散式濾波架構的方法都能利用各個傳感器自身的計算能力進行本地狀態估計，也需要中心節點利用各個傳感器的狀態估計結果和協方差矩陣進行融合，與集中式濾波相比，分散式濾波將計算量分配到各個傳感器節點中，降低了中心節點的計算負擔。聯邦濾波中，若所有子濾波器的狀態均為公共狀態，則狀態融合精度與集中濾波器精度相同。可以認為，聯邦濾波通過將狀態拆分為公共狀態和私有狀態，實現了狀態向量融合方法在各個傳感器狀態估計不相關條件下異質傳感器網絡的融合狀態估計。

3)基于一致性的分布式濾波架構：估計一致性、觀測一致性、信息一致性。

分布式濾波架構基于一致性算法，在不依賴中心節點的情況下可以實現連通傳感器網絡的分布式狀態估計，與集中式和分散式架構相比，分布式架構降低了計算量，并且提高了系統的魯棒性，便于故障診斷。本文指出，信息一致性方法實質上是分布式地實現了狀態向量融合的保守估計。