MEMS陀螺儀的高精度標定方法

陳海明，李榮冰，王雙甲，劉建業

(1.南京航空航天大學導航研究中心,南京 211106；2.西安飛行自動控制研究所,西安 710065)

0 引言

微機電(Micro-Electro-Mechanical System，MEMS)陀螺儀作為MEMS傳感器典型代表之一，具有體積小、成本低、功耗低和可靠性高等優點，是慣性導航領域的研究熱點。MEMS陀螺儀由于機械結構或制造過程中引入的機械誤差，幾乎都存在因加速度產生的測量誤差，該誤差被稱為加速度敏感漂移誤差。過去針對MEMS陀螺儀的建模研究中，因為研究對象的測量精度較低，大多只考慮了零偏誤差、非正交誤差和標度因數誤差對陀螺儀測量精度的影響，沒有考慮加速度敏感漂移誤差。近年來，隨著MEMS陀螺儀在電子學控制、微結構、工藝平臺以及集成應用技術等方面取得突破，其測量精度得到了明顯提高，而建立考慮加速度敏感漂移誤差的MEMS陀螺儀輸出模型是提高其測量精度，使其在更高精度導航領域應用的重要前提。

一般情況下，陀螺儀和加速度計組成慣性測量單元，用于測量角速率和加速度。其中，角速率測量單元由陀螺儀構成，其輸出角速率包含非正交誤差和與輸入加速度相關的加速度敏感漂移誤差。為了提高陀螺儀的測量精度，本文設計了一種同時標定MEMS陀螺儀非正交誤差和加速度敏感漂移誤差的標定方法，該方法適用于零偏穩定性優于1(°)/h的MEMS陀螺儀，并通過試驗進行了驗證。標定過程中，加速度數據由慣性測量單元中的加速度計提供，且加速度計軸向與陀螺儀軸向重合，因此，加速度計輸出數據在經過誤差修正后就是陀螺儀對應軸向的加速度值。

1 包含加速度敏感漂移誤差和非正交誤差的MEMS陀螺儀誤差建模

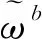
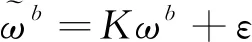
(1)

其中，為標度因子；為零偏誤差。

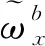
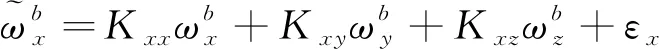
(2)

根據加速度敏感漂移誤差定義，陀螺儀的加速度敏感漂移誤差與陀螺儀所受比力之間的關系可以表示為

=++

(3)

其中，、和分別是陀螺儀在3個軸向上受到的比力；、和分別是各軸向比力對陀螺儀的加速度敏感漂移系數。

結合式(2)與式(3)，可以得到考慮非正交誤差與加速度敏感漂移誤差的軸陀螺儀輸出模型

+++

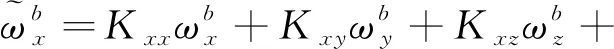
(4)

同理可得軸和軸陀螺儀輸出模型

+++

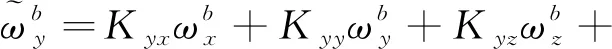
(5)

+++

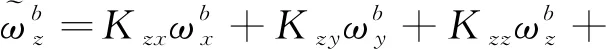
(6)

矩陣表達式可以表示為

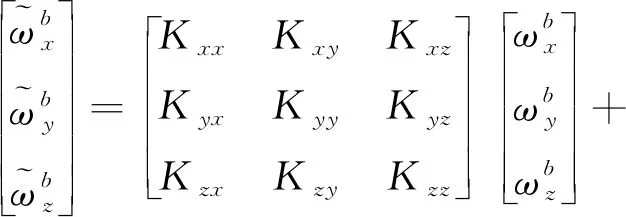
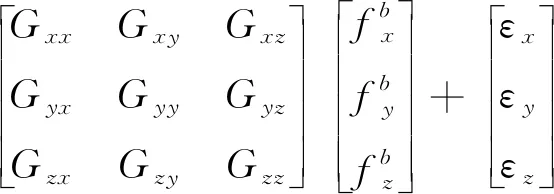
(7)

可簡化為

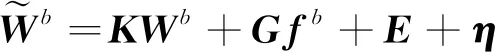
(8)

其中，為零偏不穩定性造成的誤差，該誤差項可以通過對角速率原始數據進行分組平滑處理后得到消除。

從式(8)可以看出，為了提高陀螺儀的輸出精度，需要標定和補償陀螺儀的零偏、非正交誤差，以及標度因子誤差矩陣和加速度敏感漂移誤差矩陣。

2 基于誤差模型解耦的非正交與加速度敏感漂移系數轉臺標定方法

傳統的陀螺儀多位置轉臺標定只考慮了陀螺儀的零偏和非正交誤差對陀螺儀輸出的影響。為了對加速度敏感漂移誤差進行標定與修正，本文設計了16位置轉臺標定方案，標定步驟如下：

1)轉動雙軸轉臺內外框，使轉臺位置依次如圖1所示，分別采集靜態下16個轉臺位置的三軸MEMS陀螺儀和加速度計的數據；

2)對采集到的陀螺儀和加速度計的數據進行分組平滑處理；

3)對MEMS陀螺儀的零偏誤差進行標定與補償；

4)同時對陀螺儀的加速度敏感漂移誤差和非正交誤差進行標定。

零偏穩定性優于1(°)/h的陀螺儀在減小噪聲的影響后可以準確地敏感到地球自轉角速率，所以本方案將選擇地球自轉角速率在3個軸上的分量作為陀螺儀的激勵角速率。

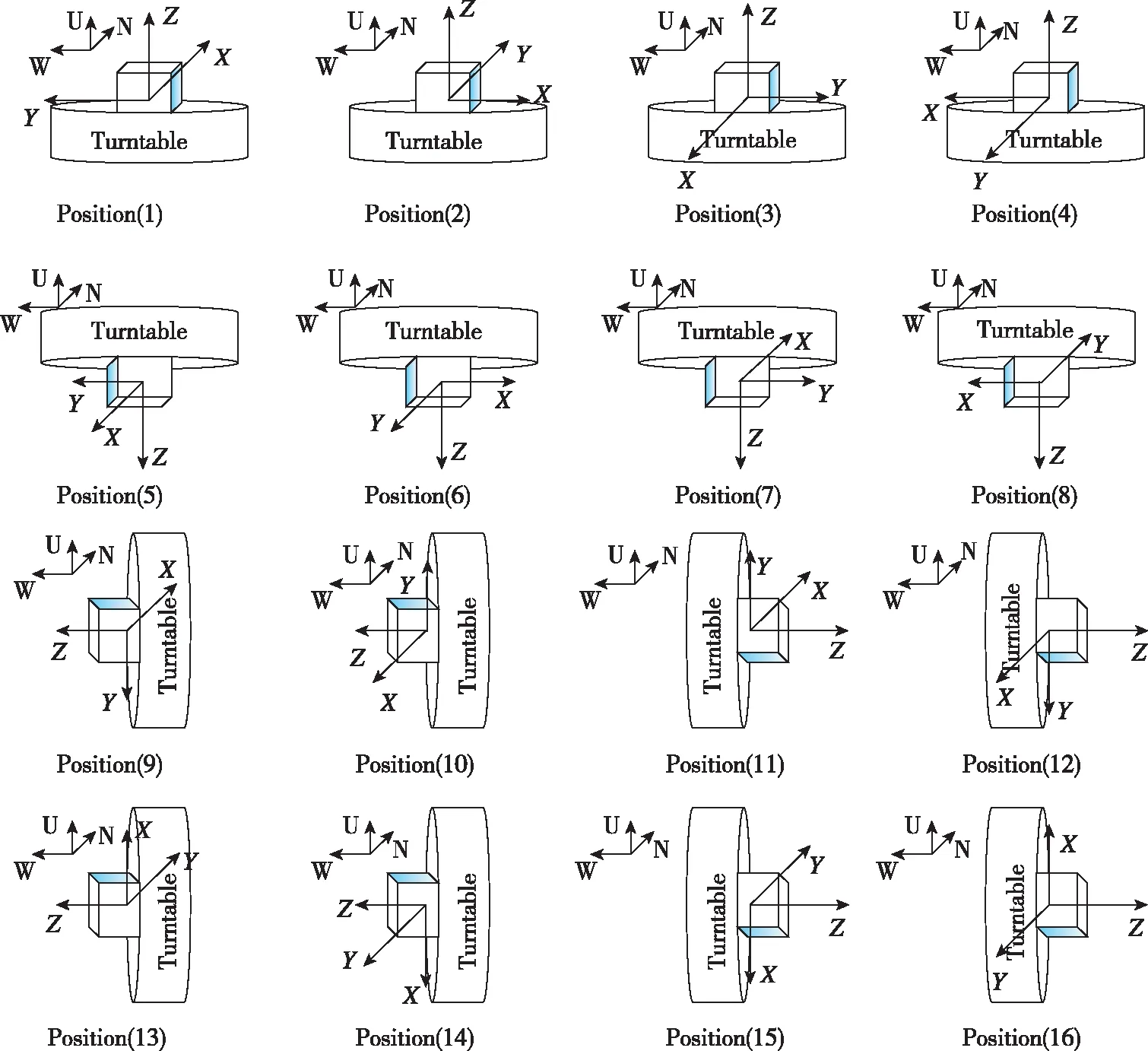
圖1 轉臺標定位置示意圖Fig.1 Position diagram of turntable

在進行轉臺位置調整時，不需要采集陀螺儀數據，所以轉臺的轉動方式不會對標定結果產生影響，只需要調整雙軸轉臺的內外框，使轉臺位置依次如圖1中所示的16個位置狀態即可。

因為需要對陀螺儀的加速度敏感漂移系數進行標定，所以需要確保每個軸向上的陀螺儀除了受到2個以上的角速率激勵外，還要受到至少2個不同數值的比力激勵。本文方法選擇-,0,作為對陀螺儀的激勵加速度，在同時考慮激勵的充分性與標定效率的情況下，設計了圖1所示的16個轉臺位置狀態。

3 零偏誤差校準

對于陀螺儀零偏的標定與補償，此處僅以軸方向上的陀螺儀作為樣例進行分析。

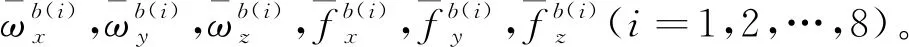
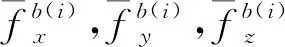
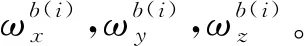
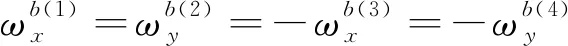
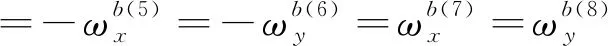
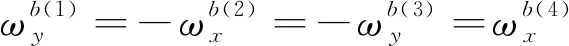
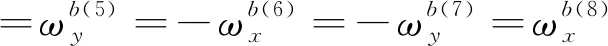
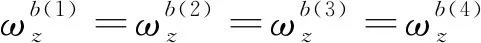
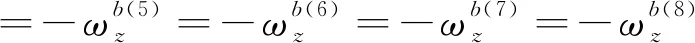
(9)

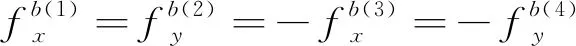
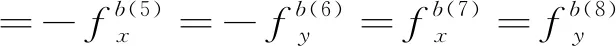
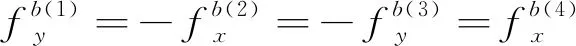
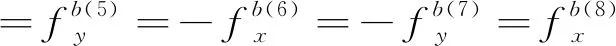
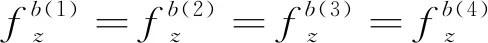
(10)

將上述式(9)和式(10)分別代入式(8)中，可以得到在前8個位置狀態下軸陀螺儀的輸出角速率與3個軸上實際的輸入角速率和比力的關系為

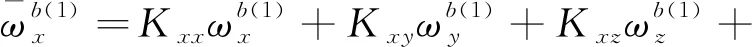
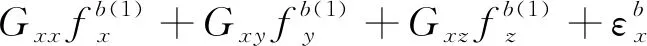
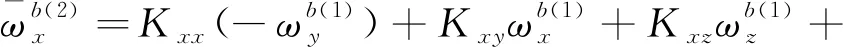
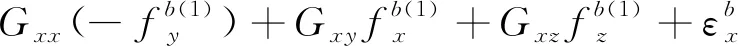
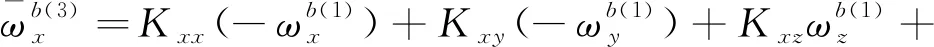
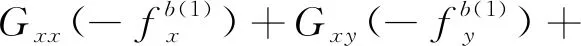
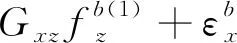
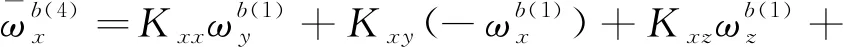
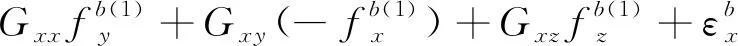
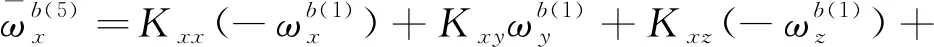
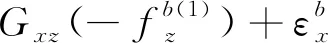
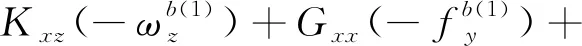
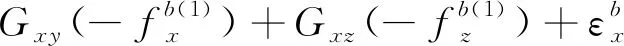
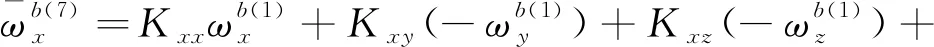
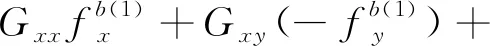
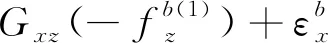
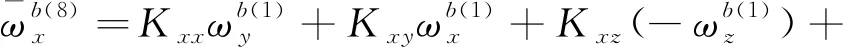
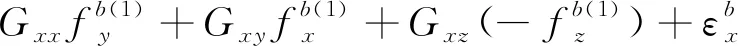
(11)

將式(11)中的8個等式左、右兩邊各自兩兩相加，不難發現，由于在狀態轉動時，位置狀態的選擇保證了外界輸入的角速率與加速度對陀螺儀輸出的影響兩兩抵消，所以軸陀螺儀的零偏誤差可以表示為

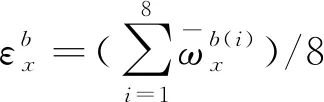
(12)

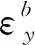
補償零偏誤差后，陀螺儀在16個位置狀態下的角速率輸出與外界施加在3個軸上的角速率與加速度的關系可以表示為

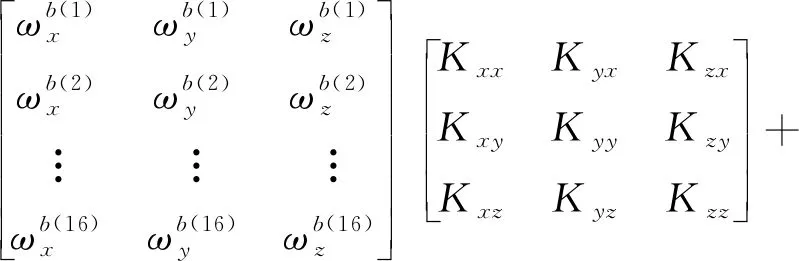
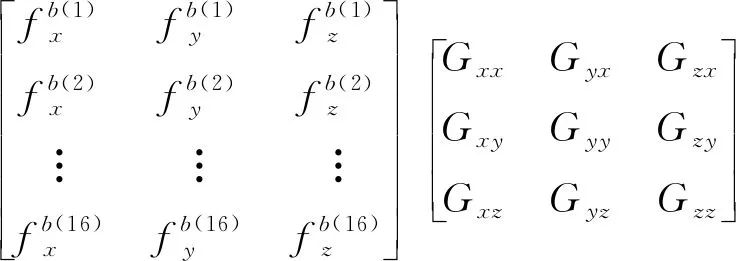
(13)

式(13)可以簡化為

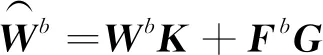
(14)

4 非正交誤差和加速度敏感漂移誤差校準

從式(14)可以看出，在補償陀螺儀零偏誤差后，陀螺儀的輸出角速率中，非正交誤差與加速度敏感漂移誤差仍然相互耦合，且很難通過物理手段將2個耦合項進行解耦。若僅僅使用數學方法，可以將式(14)等式右側的與合并為一項，得到

(15)

此時,可以利用最小二乘法對方程式(15)直接進行擬合求解，但因為矩陣中數值接近于0的元素較多，所以矩陣接近于奇異矩陣，最終導致矩陣方程求解的誤差較大。因此，需要改進對非正交誤差和加速度敏感漂移誤差的標定方法。

本文利用兩組測量數據，分別計算加速度敏感漂移誤差矩陣與非正交誤差矩陣并相互迭代，對這2個誤差矩陣進行求解。下面給出迭代方法。

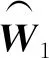
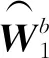
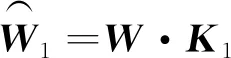
(16)

因為不是奇異矩陣，此時利用最小二乘法的求解法則，對超定方程式(16)中的進行如式(17)所示的擬合求解，即可得到所需標定的非正交誤差矩陣

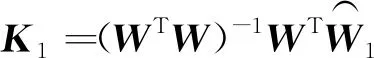
(17)

根據第一組數據計算出非正交誤差矩陣，并將該結果代入第二組數據，得到

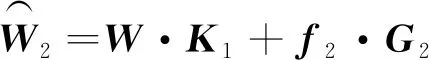
(18)

同理，可以通過最小二乘法解算超定方程式(18)，求得加速度敏感漂移誤差矩陣，然后將結果代入第一組數據，對非正交誤差進行更新。每次迭代，以經過校正后的陀螺儀對地球自轉角速率的敏感誤差作為對迭代結果準確性的評估依據。如此循環往復，在多次迭代后，可以得到較為精準的非正交誤差矩陣和加速度敏感漂移誤差矩陣。

在完成對非正交誤差、加速度敏感漂移誤差和陀螺儀零偏的標定后，根據式(19)可以得到經過修正后的更高精度的陀螺儀輸出

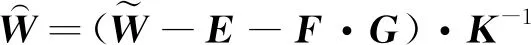
(19)

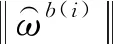
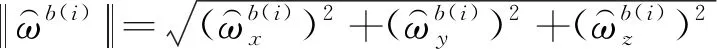
(20)

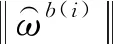
(21)

(22)

5 非正交誤差和加速度敏感漂移誤差校準方法驗證與分析

本文選用了高精度雙軸溫控轉臺進行16個位置的轉臺標定，并采用3個國產高精度MEMS陀螺儀和3個MEMS加速度計構建了姿態測量單元，對上文闡述的標定方法進行驗證。選用的3個陀螺儀實測輸出零偏不穩定性分別達到了0.731(°)/h、0.367(°)/h、0.916(°)/h，Allan方差曲線達到最低點時的采樣時間分別為655s、681s、622s。

進行陀螺儀轉臺標定時，轉動轉臺內外框，使轉臺位置依次滿足圖1中16個位置狀態，每個位置處數據采集時長為20min。在完成了一個位置狀態下的數據采集后，根據Allan方差分析曲線最低點處的采樣時間對原始數據進行分組平滑，以減小零偏不穩定性的影響。

在陀螺儀Allan方差分析曲線達到最低點時，采樣寬度與采樣間隔和采樣數據量之間存在以下關系

=·

(23)

以為分組長度，分別將3個軸的陀螺儀原始輸出數據分割成(=,,)組，與每個軸陀螺儀輸出數據總量的關系為

=-+1

(24)

其中，第組數據是陀螺儀輸出的總體數據中第個數據到第+-1的數據。

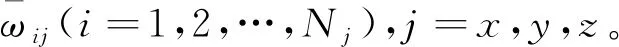
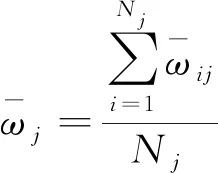
(25)

根據分組平滑后的陀螺儀在位置狀態(1)處～(8)處的數據，按式(11)求取3個軸向上的陀螺儀的零偏，分別為-1.709(°)/h、30.633(°)/h和-3.380(°)/h。

采用上文闡述的迭代解算方法對角速率測量系統的非正交誤差和加速度敏感漂移誤差進行求解。在迭代過程中，初始迭代誤差為2.64(°)/h，在迭代超過800次后，每次迭代時誤差的降低約為1×10(°)/h，此時迭代已趨于穩定，約1.29(°)/h。標定結果分別如表1和表2所示。

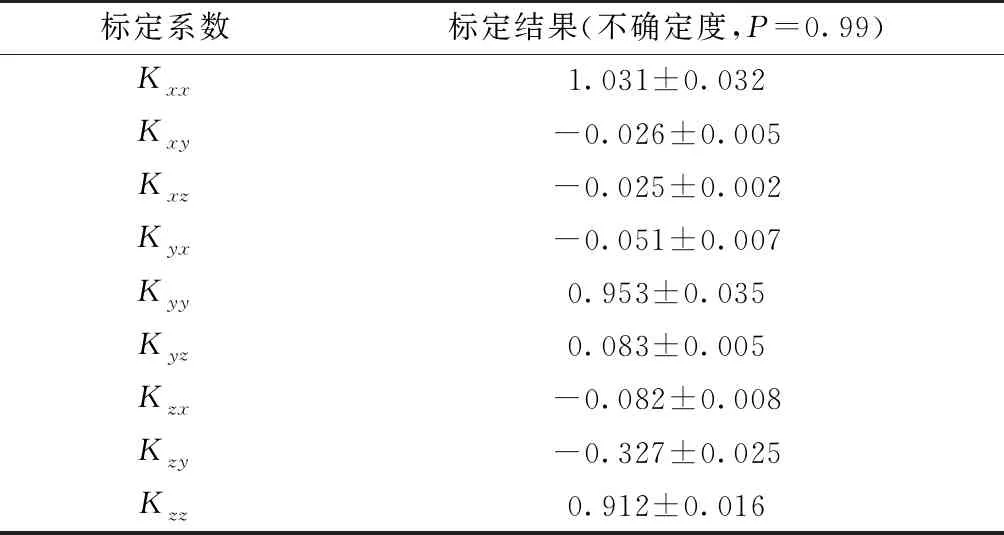
表1 陀螺儀非正交誤差系數標定結果

表2 陀螺儀加速度敏感漂移誤差系數標定結果

從表2可以看出，某軸向加速度對該軸向陀螺儀的影響并不一定是最大的，加速度敏感漂移誤差對陀螺儀輸出的影響是綜合性的。

本文選用的加速度計的零偏穩定性為100μ，由加速度測量誤差引起的陀螺儀加速度敏感漂移誤差的最大值約為0.18(°)/h。

本文陀螺儀標定方法的標定結果與常規標定方法所得結果的對比如表3所示。

由表3可以看出，本文提出的16位置標定方法與傳統的6位置和19位置的陀螺儀標定方法精度相當。但相較于傳統的6位置標定方法，16位置標定方法不需要頻繁地改變對陀螺儀的角速率激勵；同時，本文方法對不同轉臺位置間的轉動方式沒有嚴格的要求，且位置狀態相對較少，所以與19位置標定方法相比操作更方便。

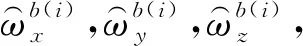
表3 16位置標定與常規的6位置標定、19位置標定結果對比

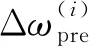
從表4和圖2可以看出，在對非正交誤差和加速度敏感漂移誤差進行標定和修正后，陀螺儀敏感地球自轉角速率誤差值Δ的均值與標準差均小于補償前，這證明了上文提出的對非正交誤差和加速度敏感漂移誤差標定可以提高MEMS陀螺儀的測量精度和性能。在經過誤差標定和修正后，陀螺儀對地球自轉角速率的測量誤差和測量標準差分別降低了55.7%和25.9%，這證明了該算法的有效性，為MEMS陀螺儀高精度建模工作提供了參考。

表4 Δωpre與Δωaft的均值與標準差

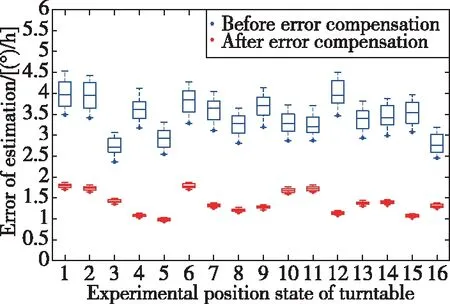
圖2 非正交誤差與加速度敏感漂移誤差補償前后Δωie對比曲線Fig.2 Δωie before and after compensating non-orthogonal error and acceleration-sensitive drift error

6 結論

本文設計了針對MEMS陀螺儀的16位置轉臺標定方案，基于慣性測量單元中MEMS陀螺儀非正交誤差和加速度敏感漂移誤差相互耦合的特性，提出了一種利用兩組角速率數據迭代求解非正交誤差系數和加速度敏感漂移誤差系數的方法。同時，本文以陀螺儀對地球自轉角速率的測量誤差作為陀螺儀輸出模型精度性能的評估依據，并展開試驗驗證。結果表明，通過對非正交誤差和加速度敏感漂移誤差的標定與修正，微慣性測量單元中陀螺儀的測量精度和性能得到了明顯的提高，為MEMS陀螺儀高精度建模工作提供了參考，為其在高精度導航領域的應用奠定了基礎。