含變速恒頻風電機組的電網運行特性仿真

陸秋瑜， 楊銀國， 于珍， 李力， 張東輝， 李海波

(1.廣東電網有限責任公司電力調度控制中心, 廣州 510000； 2.清華四川能源互聯網研究院， 成都 610000)

風能作為一種清潔、可持續并且對生態友好的能源，其優越的性能被越來越多的學者所認識。近幾年來風力發電技術不斷發展，單機容量也逐步增大，其安全性和可靠性越來越明顯。隨著風力發電場的建設規模在不斷擴大，變速恒頻風機組調速范圍大且成本低的優勢體現出來[1]。隨著風力發電規模和占比的提高，對于風力發電的兼容性、安全性和對于電網的穩定性的影響規律的研究需要完善。

近年來，中外學者針對變速恒頻風力發電已經進行了深入細致的研究，隨著風力發電技術的不斷發展，風電抗干擾能力薄弱的問題逐漸突顯出來[2]。目前，針對風力發電存在較多的問題，電網母線電壓的波動對風力發電機組穩定性的影響、并網過程中電網是否穩定以及電能的質量問題[3]。基于此，李文津等[4]對風機定子和轉子分別采用不同的控制策略，從而使風機可以穩定并網。錢敏慧等[5]提出了預報及校正變槳的控制策略，能夠調節不同風速環境中，風機轉速，獲得合適的風能捕獲。靳雯皓等[6]進一步優化控制策略，采取混合儲能系統的控制策略，從而提升系統儲能裝置的利用率。劉其輝等[7]考慮到空載和負載狀態下的并網策略，并分別采用定子磁鏈控制和轉子電流控制策略。宋文靜等[8]設計一種改進的非線性函數，能有效提升系統在不同風速條件下的抗擾能力。李嘯驄等[9]將風電機組構建非線性數學模型，然后設計了非線性控制器，提升功率調節能力。文獻[10]提出了一種配備調速差動機構(speed regulating differential mechanism,SRDM)的混合動力傳輸系統，可以做到在不同風速、諧振和負載突變等情況下保證頻率恒定。目前大多數研究者通過研究得出的一些結果都是在一些簡化模型的基礎上得到的，主要攻堅控制理論[11]。但控制策略研究需要建立在了解各參數對風機及系統的具體影響的基礎上，目前，針對風力發電機組在并網及外部故障對電力系統穩定性的實際影響研究比較少，而且絕大部分只是停留在建模仿真階段。

為了研究風速及故障在風電并網時對電力系統的影響，現根據風力發電機組的結構原理建立數學模型，通過使用Simulink模塊來搭建風力發電機組各部件系統的仿真模型及風力發電系統模型，然后將搭建的風力發電機模型與電網模型進行并網運行仿真，研究不同風速下風力發電機組并網對電網的影響，以及不同故障下風力發電機對電網運行穩定性的影響。

1 風機基礎及數學模型

1.1 變速恒頻風電機組結構與運行原理

由于風速是隨機不定的，風力發電機輸出電能的多少會隨實時風速的大小、方向的變化而變化，因此保證風力發電機輸出功率恒定對風力發電機組所并電網的穩定性具有重要意義[12]。變速恒頻風力發電機保持頻率不變的方法分為：風速變化引起風輪轉速變化時，通過控制發電機轉子繞組中勵磁電流的頻率和旋轉磁場轉速達到恒頻的目的；風力發電機組在并入電網過程中，連接整流裝置進行整流，控制開關電路逆變輸出，經濾波器濾波，得到輸出恒定且與發電機轉速大小無關的恒頻正弦波。后者較為方便簡潔，本文研究采取第二種方式進行變速恒頻控制。變速恒頻風力發電機組可分為如圖1所示幾個基本模塊。風通過作用在風力機葉片上，使風輪隨風速旋轉，風輪的轉速通過傳動系統部分的齒輪箱增速，將轉速提高至發電機的額定轉速，使之帶動發電機轉子旋轉，并達到使機械能轉化為電能的目的。

圖1 變速恒頻風力發電機基本結構圖Fig.1 Basic structure diagram of variable speed constant frequency wind turbine

1.2 變速恒頻風電機組數學建模

為簡化風速模型，采用組合風速模型，組合風速模型是將基本風、漸變風、陣風、隨機噪聲風4種風進行疊加。組合風速模型的數學模型為

V=VB+VZ+VJ+VS

(1)

式(1)中：VB為基本風分量；VZ為陣風分量；VJ為漸變風分量；VS為噪聲風分量。

由于本文的重點是風輪葉片在風力發電系統中的能量轉換過程，所以可以使用風能利用系數建立風輪的簡化空氣動力學模型。風力發電機能量轉換模型的功率和風輪葉片轉矩大小的計算公式是根據流體力學中氣流的動能計算公式推導得到的[12]。風力發電機的輸出機械功率為

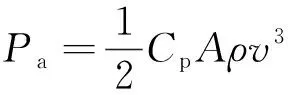
(2)

式(2)中：Pa為風力機的機械輸出功率；A為風力機的掃風面積；Cp為風力機的利用系數；ρ為空氣密度；v為風速。

由于采用的變速恒頻風力發電機不是直驅式的，而是風輪經轉軸連接低速轉軸、變速齒輪箱、高速轉軸再連接至發電機轉子所構成的傳動系統，所以傳動系統模型可以采用典型的三質量塊模型，分別考慮風力發電機風輪的質量塊、變速齒輪箱的質量塊和發電機的質量塊，風力發電機傳動系統的等效模型，如圖2所示。

Twtr為風力發電機風輪的轉矩；Jwtr為風力發電機風輪的轉動慣量；Ωwtr為風力發電機風輪的機械角速度；Kswtr為風力發電機組中風輪等效扭轉硬度的彈簧系數；Tgen為發電機的轉矩；Jgen為發電機模塊的轉動慣量；Ωgen為發電機模塊的機械角速度；Ksgen為發電機部分的等效扭轉硬度的彈簧系數；T1為進入齒輪箱的轉矩；T2為從齒輪箱輸出的轉矩，T2=(1/Kgear)T1；Kgear為齒輪 箱的變比系數；Ω2=KgearΩ1圖2 風力發電機傳動系統三質量塊模型示意圖Fig.2 Schematic diagram of three-mass model of wind turbine drive system

一質量塊模型的優點在于通過簡化其方程數量，減少到只有一個系統方程，在系統仿真計算中將大幅度加快模型的仿真速度。采用一質量塊模型，將風輪和發電機兩系統之間的相互作用等效到一端，從而簡化傳動系統建模及風力發電機傳動系統模型。因此得到風輪的運動方程為

(3)

式(3)中：Jr為風輪的轉動慣量；Ω為風輪葉片的轉動角速度；假定阻力全部集中在風輪處，則TD為能量傳遞裝置中全部阻力矩；Twtr為風輪從風能吸收的動力矩；Tm為高速軸上的阻力矩；k為齒輪傳動比;t為時間。發電機的運動方程為

(4)

式(4)中：Jg為發電機的機械轉動慣量；Te為發電機上的反作用扭矩；Tm為高速軸上的轉動扭矩；ωg為發電機的機械角速度。傳動系統的一質量塊模型為

(5)

2 變速恒頻風電機組并網運行仿真分析

2.1 風電機組并網技術概述

當風力發電機組進行并網時，為避免并網過程中產生過大的沖擊電流和沖擊轉矩，要求輸出端的三相參數，其瞬時值要與并網處電網的參數對應相等，即波形、幅值、相位、頻率、相序對應相等。并網模型結構如圖3所示。

圖3 變速恒頻風力發電機的并網模型Fig.3 Grid-connected model of variable-speed constant-frequency wind turbine

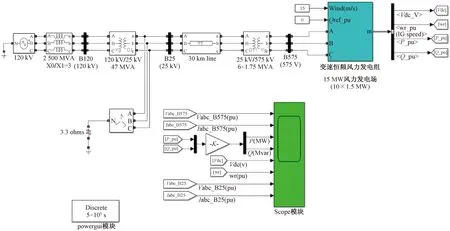
line為輸電線路；ohms為輸出端；K表示將標幺值轉化為實際值；V為并網處電壓；I為并網處電流；P為風力發電機組輸出有功功率； Q為風力發電機組輸出無功功率；均采用標幺值，單位p.u.；Wind處設置風速。圖4 風力發電機并網模型Fig.4 Wind turbine grid-connected model

利用MATLAB中的Simulink模塊搭建出各系統部件的仿真模型，并分別對搭建的仿真模型進行運行仿真。

風速模型設置隨機風速的采樣時間為0.05 s，陣風在4 s時加入，持續10 s，陣風的最大風速設為6 m/s，設置額定風速即平均風速為11.7 m/s，階躍風速的啟動時間為20 s，在25 s結束，階躍風保持3 s，階躍風的峰值為6 m/s，仿真時間為50 s。根據輸出的風速波形可以看出，輸出的實時風速會根據陣風、階躍風、隨機風的大小在平均風速的基礎上波動。當設置輸入的平均風速在11.7 m/s時，將四風速通過疊加后得到的風速在15～20 m/s。

并網模型如圖4所示。設置風力發電機風輪葉片的半徑為40 m，大氣中空氣密度為1.25 kg/m3，風力發電機的切入風速為3 m/s，切出風速為25 m/s，仿真時間為50 s。設置調制的頻率為50 Hz。將10個1.5 MW大小的風力發電機組合成15 MW的風力發電場，通過母線和變壓器連接到25 kV的電網，通過30 km的輸電線向120 kV電網輸出電力。

3 仿真實例與分析

根據圖4所示的仿真模型分別分析風電機組在不同運行狀態下的輸出狀態。

3.1 不同風速條件下仿真結果分析

當輸入風速的平均風速為5 m/s時，得到的并網仿真結果如圖5～圖8所示。

圖5 平均風速為5 m/s時并網結果Fig.5 Grid connection results when the average wind speed is 5 m/s

圖6 平均風速為11.7 m/s時并網結果Fig.6 Grid connection results when the average wind speed is 11.7 m/s

由圖5可知，風力發電機組輸出的無功功率最大值可達到16.47 MVar，有功功率最大值為27.14 MW，風力發電機并網處的電壓的最大值為1.431 p.u.，電流最大值為5.139 p.u.；由圖6可知，風力發電機組輸出的無功功率最大值可達到17.89 MVar，有功功率最大值為27.42 MW，風力發電機并網處的電壓參數的最大值為1.428 p.u.，電流最大值為5.242 p.u.；由圖8可知，風力發電機組輸出的無功功率最大值可達到15.69 MVar，有功功率最大值為26.23 MW，風力發電機并網處的電壓的最大值為1.412 p.u.，電流最大值為4.948 p.u.。

圖7 平均風速為20 m/s時并網結果Fig.7 Grid connection results when the average wind speed is 20 m/s

圖8 平均風速為25 m/s時并網結果Fig.8 Grid connection results when the average wind speed is 25 m/s

上述仿真數據可知，當風力發電機組在低風速和額定風速下運行時并網處的電壓、電流數值相差不大，但在較高風速、臨界風速下運行時，風力發電機輸出的電壓、電流都會明顯下降，并且因為當風力發電機在額定風速下運行時并網點處的電流最大，證明在額定風速時風電機組對輸入風能的轉化效率高。另外，當風力發電機組在高風速和低風速下運行時，風力發電機組輸出的無功功率、有功功率都比在額定風速下輸出的少，并且當風速達到20 m/s以上時，風力發電機輸出的有功、無功功率和達到臨界風速時輸出的相差不大，又因為無功功率和有功功率分別對電網電壓幅值和電力系統頻率的穩定有重要作用，所以當風力發電機在達到額定風速附近并網時，更有利于電網系統的穩定。

3.2 不同故障下仿真結果分析

當風力發電機組并網的外部系統發生短路故障所產生的沖擊短路電流會給電力系統的電氣設備帶來巨大的沖擊，嚴重影響電力系統運行的穩定性。電網實際運行中發生的簡單故障有：單相發生接地短路、兩相相間發生短路、三相短路和兩相發生接地短路故障。本文討論風力發電系統外部發生簡單故障時，風力發電系統并網對電網系統穩定性的影響，因此模型中設置故障點在25 kV母線處，電網故障分析模型如圖9所示。

V為并網處電壓；I為并網處電流；P為風力發電機組輸出有功功率；Q為風力發電機組輸出無功功率；均采用標幺值； Wind處設置風速；閃電位置為故障發生處圖9 風力發電系統并網后電力系統故障分析模型Fig.9 Power system failure analysis model after wind power generation system is connected to the grid

假設在靠近25 kV母線處發生三相接地故障，故障在0.1 s開始持續0.2 s，電網模型得到的仿真輸出結果如圖10所示。

當靠近25 kV母線處發生三相短路故障時，25 kV母線處的電壓從正常運行時的1.031 p.u.降低為0 p.u.，母線電流從2.768 p.u.迅速提升到27.28 p.u.，產生了10倍左右的沖擊電流，巨大的沖擊電流將會對絕緣設備的壽命造成嚴重影響，電壓的消失將會給電網系統的穩定性帶來嚴重的威脅。

圖10 發生三相短路故障后各參數波形Fig.10 Waveforms of various parameters after a three-phase short-circuit fault occurs

另外，風力發電機組并網母線處的電壓、電流趨于平緩，相比于不發生三相短路故障時的電壓、電流有明顯的下降。在風力發電機組正常運行時，風力發電機組輸出的有功功率為27.42 MW，而故障發生后輸出的有功功率甚至減小到1.6 MW左右，輸出的無功功率也從正常運行時的17.89 MVar減少到12 MVar左右，大幅度減少的P和Q，將會造成電網系統的功率缺額，給系統電壓、頻率帶來擾動，對供電端的輸出大幅減少，不利于電力系統的穩定運行，三相短路故障對電力系統穩定性影響較大。

假設在靠近25 kV母線處發生A、B兩相相間短路故障，故障在0.1 s處開始持續時間0.2 s，電網模型得到的仿真輸出結果如圖11所示。

圖11 發生兩相短路故障后各參數波形Fig.11 Waveforms of various parameters after a two-phase short-circuit fault occurs

當靠近25 kV母線處發生A、B兩相相間短路故障時，25 kV母線處A、B相的電壓從正常運行時的1.031 p.u.降低為之前的一半左右，但A、B相電壓未完全消失，并且A、B相電流從之前的2.9 p.u.提高至23.74 p.u.，產生小于10倍的沖擊電流，而C相電壓、電流幾乎保持不變，因此A、B、C三相的電壓電流不再對稱相等，影響電網系統的系統穩定性。

另外，從圖11中可以看出風力發電機組輸出的無功功率大約在10 MVar附近波動，遠遠低于正常運行時輸出的無功功率17.89 MVar，并且風力發電機組輸出的有功功率也從正常運行時的27.42 MW減小到10 MW左右，需要額外地向電網系統中補送有功功率和無功功率的缺額，影響系統電壓、頻率的穩定，不利于電力系統的穩定運行。當A、B兩相相間短路故障時，C相仍可以正常運行，因此相比于三相短路故障對電網穩定性的影響，兩相相間短路故障對系統的影響較小。

假設在靠近25 kV母線處發生A、B兩相接地短路故障，故障在0.1 s處開始持續時間0.2 s，電網模型得到的仿真輸出結果如圖12所示。

圖12 發生兩相短路接地故障后各參數波形Fig.12 Waveforms of various parameters after a two-phase short-circuit to ground fault occurs

當靠近25 kV母線處發生A、B兩相接地故障時，25 kV母線處A、B相電壓從1.212 p.u.減小至0，A、B相電流從正常運行時的2.929 p.u.迅速增長為26.15 p.u.，產生小于10倍的沖擊電流，產生的沖擊電流將會對絕緣設備的壽命造成嚴重影響，但由于C相正常，因此C相可以繼續輸送電能，但電網系統失去了對稱性。

另外，從圖12中可以分析出風力發電機組輸出的無功功率在10 MVar附近波動，其輸出波形類似于兩相相間短路，同樣，其輸出的無功功率也遠遠低于其正常運行時輸出的無功功率17.89 MVar，并且風力發電機組輸出的有功功率也從正常運行時的27.42 MW減小到10 MW左右，所以需要額外的向電網系統中補送有功功率和無功功率。通過對比分析兩相接地短路故障與兩相相間短路故障，由于兩相接地短路故障處母線的A、B相電壓完全消失，使A、B、C三相嚴重不對稱，因此兩相接地故障對電力系統穩定性的影響更大，但由于兩相接地短路故障存在非故障相，因此其對電網系統穩定性的影響程度小于三相短路故障對電網穩定性的影響，介于三相短路故障與兩相相間短路故障之間。

假設在靠近25 kV母線處發生A相接地短路故障，故障在0.1 s處開始持續時間0.2 s，電網模型得到的仿真輸出結果如圖13所示。

圖13 發生單相短路接地故障后各參數波形Fig.13 Waveforms of various parameters after a single-phase short-circuit to ground fault

當靠近25 kV母線處發生A相單相接地短路故障時，25 kV母線處A相電壓從1.736 p.u.變為0，并且A相電流從2.545 p.u.變為14.24 p.u.，產生7倍左右的沖擊電流，產生的沖擊電流將會對絕緣設備的壽命造成嚴重影響，由于僅僅A相發生接地故障，B、C相仍然可以正常運行，所以造成電網系統的不對稱程度增強，會對電力系統穩定性帶來影響。

另外，從仿真結果圖13中可以看出，風力發電機組輸出的無功功率約為20 MVar，相比于正常運行時輸出的17.89 MVar大幅提高，這將會造成電力系統中無功功率過剩，不及時處理會出現容升效應，對電力系統的絕緣帶來威脅。此外，風力發電機組輸出的有功功率幾乎不變(約為27.42 MW)，因此單相接地短路故障對電力系統頻率影響較小。

4 結論

通過搭建了風力發電機組的各個系統組件，其中包括：實時風速仿真模型、風輪仿真模型、傳動系統仿真模型、發電機仿真模型和頻率調制系統仿真模型，通過搭建模型和仿真，計算了不同風速和不同故障下，功率、電壓和電流的變化情況。

(1)風力發電機組輸出的功率及并網處電壓電流在低風速和額定風速下運行時相差不大，但在較高風速下運行時，風力發電機輸出的并網電壓和電流會下降。

(2)當風力發電機組外部電網線路中發生三相接地短路故障時，故障點處的母線電壓會從1.031 p.u.降低為0，并會產生10倍左右的沖擊電流，輸出的有功功率從正常運行時的27.42 MW減小到1.6 MW左右。

(3)電力系統穩定性影響程度最大的是三相短路故障，其次是系統發生兩相接地短路故障，接著是兩相相間短路故障，其中故障后對電力系統穩定性影響程度最小的是發生單相接地短路故障。