數據點位置低延時智能挖掘方法與仿真

唐雯煒，李志敏

(浙江中醫藥大學信息技術中心，浙江 杭州 310053)

1 引言

信息化進程腳步的加快，使得數據庫技術也取得突飛猛進的發展，同時信息系統的存儲壓力和計算壓力也隨之增加。面對數據庫中的海量數據，從中獲取部分有價值的信息難度較大，且當前的信息提取方法步驟較為繁瑣。因此，如何在數量巨大的數據中快速找到數據點所在的位置、挖掘其隱含的信息已經成為了日后重點研究方向。

針對數據點位置的挖掘問題，相關領域研究學家們也對此展開了深入研究。文獻[1]利用人工智能裁決機制對網絡的挖掘寬度、網絡環境以及節點存儲大小等多方面因素進行綜合考慮，確定這些因素對挖掘效果產生的影響程度，以此獲得數據挖掘的難易程度。然后，通過所得結果采取強化措施來提高算法的挖掘效率，但是挖掘精度有待提高；文獻[2]利用智能網絡系統對低匹配度的數據進行了研究。首先，對數據進行預處理，使其轉換為便于挖掘的規約形式，在一定程度上確保算法具有更高的挖掘效率；然后，對算法的挖掘規則利用神經網絡模型進行更新，同時剔除掉其中包含的冗余連接節點；最后，通過I/O輸出完成挖掘的數據。該方法對低匹配度的數據具有較為理想的效果，但并不適合處理高維或多模態數據。

為解決以上傳統方法的缺陷，提出基于并行FP-Growth算法的數據點位置智能挖掘算法。結合并行FP-Growth算法與MAP/Reduce并行編程模型，形成新的FPPM算法。該算法通過計算與之對應的局部頻繁項目集，整合在一起得到全局頻繁項目集，并計算每個項目集屬性，利用增量分類的方法找出最佳屬性，同時統計每個屬性出現的次數，利用構建的決策分支樹實現對數據點位置地準確挖掘。在仿真中，本文方法較傳統方法相比在CPU占用率、挖掘時延、信息熵方面均取得了理想的結果，并且具有理想的可擴展性。

2 FPPM算法優化建立

2.1 并行FP-Growth算法

利用并行FP-Growth算法實現數據挖掘主要是通過頻繁模式增長的方式來實現的。首先，算法掃描待識別的事務數據集D，得到一個緊湊且包含事務集中所有頻繁模式信息的頻繁模式樹[3]，完成數據點的位置挖掘。

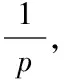
頻繁模式樹的建立過程主要通過以下四個步驟完成：

1)對處理器的每個處理過程都分配與之個數相等的事務集；

2)每個處理過程計算局部頻繁項集的計數；

3)將所有局部頻繁項集的計數[6]整合在一起，得到全局頻繁1-項集；

4)根據全局頻繁1-項集對所有處理過程進行掃描，并將全局頻繁1-項集中的節點與局部頻繁項集中的節點連接在一起，形成頻繁模式樹。

全局頻繁1-項集與局部頻繁模式樹在連接的過程中，形成了一種連接網絡，這個網絡就是FP-tree，同時也是實現數據點位置挖掘的有力保障。

2.2 FP-tree建立

FP-tree中，通常以“null”作為樹的根節點。隨機選取一個節點a，在從根節點延伸出的路徑中，將不包含a所在的部分路徑稱之為a的前綴路徑，a則是該條路徑的后綴項。前綴路徑不斷延伸，始終都有a的存在，當這些路徑在某個節點相交時，即可得到a的條件模式基。由條件模式基可以構建條件模式樹[7]，在條件模式樹下再進行數據點位置的挖掘，可以快速得到頻繁模式下的數據。

將事務數據集定義為D、最小支持度設置為2，通過表1的事務集建立如圖1所示的FP-tree。

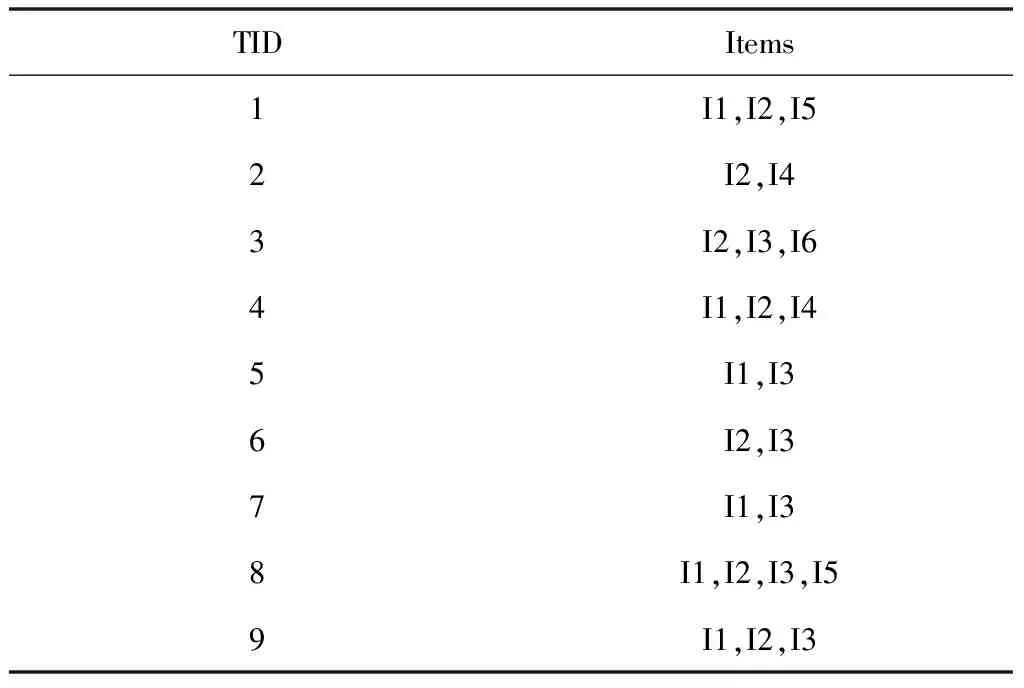
表1 事務數據集D

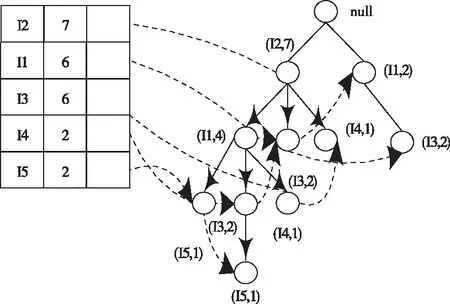
圖1 構建的FP-tree

2.3 Map/Reduce并行編程模型

Map/Reduce在處理數量巨大的挖掘工作時，會分配給每一個主節點以及其下一層的各個分節點來共同完成工作，最后將各個分節點的數據整合在一起，即為最終的挖掘結果。換句話說，Map/Reduce的主要工作是分配任務與匯總結果。將分配任務與匯總結果用函數表示為：Map和Reduce。這兩個函數的主要任務就是處理輸入鍵值對。

在Map函數中，數據的格式發生改變，以分片的形式存在，而Mapper存在于每一個分片上。首先，在Map函數中輸入鍵值對為的數值，計算后得到結果為[]的數值，根據鍵值[8]的不同對其進行排列，相同的則劃分在>元組內；最后，將劃分結果傳送至Reducer模塊中。

在Reducer這個階段中，Reducer將從不同Mapper傳送來的元組整合在一起，利用reducer函數處理>，以此獲得新的鍵值對，并將reducer函數輸出結果引入到HDFS中。

2.4 FPPM算法框架

將并行FP-Growth算法與Map/Reduce并行編程模型整合在一起，得到FPPM算法。

FPPM算法實現過程為：

1)對D中1-項集的支持數進行具體數值的計算：初始化一個統計頻繁項目集的Map/Reduce job，將輸出結果存儲在分布式緩存模塊中；

3)篩選候選全局頻繁項目集，并對其進行統計運算：重新初始化一個Map/Reduce job，將步驟2)中存儲在分布式文件內的元組進行支持度的計算，最終得到最小支持度下的頻繁項目集，在全局頻繁項集中進行匯總。

步驟2)和步驟3)所得計算結果即為數據點位置的全局頻繁項目集。

3 數據點位置智能挖掘

3.1 選取候選屬性子集

將t定義為時間。隨機選定一個時刻t，將D中的全部數據傳輸至reducer函數中，傳輸過程如式(1)所示

Dt=[Xt，Yt]

(1)

式中，X、Y分別表示數據集中數據的屬性[10]。設定一段時長為T的時間段，選取其中某個時刻并將其標記為t=1，2，…，T，將這個時間段以內的數據標記為DT，算法如下

(2)

用H(.)來表示并行FP-Growth算法的功能，通過運用貪婪算法實現最優FP-tree的構建。算法中，H(.)的主要作用為計算數據點位置的信息增量[11]，并且按照由高到低的順序對每個分支點的邊界輸入相應的標簽信息，然后選取分類的最佳屬性Xi。對于所選取的最佳屬性Xi，檢索i(i≤M)和j(j≤N)，其中，M表示屬性個數的最大值，N表示接收實例個數的最大值，也可以看作是xij的分支值。因此，從xi1到xij的分支值中選取滿足xij=arg maxH(xij)條件的功能屬性Xi。

為確保輸入結果是全局最優解[12]，在以上計算過程中，就要使所有數據點的位置都在DT中，計算公式如式(3)所示

(3)

在任意時刻t下，將Xt定義為將要篩選的全部新數據集，在集合{Ytk}中整合數據點位置信息。{Ytk}中，k為在可能集合K中的任意一個可能集合序列號。

根據當前所篩選的頻繁項目集，本文將FPPM算法按照最優分類的原則計算，計算過程如式(4)所示

(4)

在時間t內，數據點位置信息已經全部匯總在DT內，并在全局頻繁項目集中以良好的形式在集合TRGLOBAL中展現出來。在時間t+1內，數據點位置信息更新到新的集合TRGLOBAL內，通過式(3)和式(4)實現自我更新，更新時間隨著t和DT的上升而不斷延長。每更新一次，所有數據點位置信息都要重新載入DT的歷史數據。

3.2 數據點位置挖掘計算

在利用FPPM算法對數據點位置挖掘時，所采集到的數據量是非常巨大的，并且伴隨著新數據點位置信息的產生處理起來也是非常繁瑣的。因此，在處理此類數據時，本文利用增量分類的方法確保算法具有理想的挖掘效果。

增量分類的方法就是在所有候選屬性數據集中，找出可靠度最佳的數據集，將這些最佳數據集整合在一起，即可得到最佳候選屬性集。在利用增量分類方法提取數據點位置的過程中，只需要操作一次，無需重復操作，因此該方法也被稱為任意算法。通過統計每個屬性值出現的次數，來構建決策分支樹。在計算過程中，Xi出現的頻率、與Xi的類Yk都通過(5)Hoffding計算得到

(5)

式中，R用來約束分類屬性，n表示同一數據集合中的個數，δ表示約束系數。在該算法中，通過兩組高值集合項推薦得到。對于任意時刻t下，Xi具有兩個最大集合值項檢測Xi，檢測結果分別為xin和xib，這兩個值均滿足條件xin=arg maxH(xij)和xib=arg maxH(xij)。通過上述的計算過程，即可完成對數據點位置的挖掘。

4 仿真研究

為驗證本文提出的基于并行FP-Growth算法的數據點位置智能挖掘算法的有效性，與文獻[1]提出的基于人工智能裁決機制的數據點位置挖掘方法、文獻[2]提出的基于智能網絡系統的數據點位置挖掘方法進行了對比仿真。仿真中所用到的數據均來自于IBM DataGen，其中包含了多達1000個種類的數據類型，所有數據的記錄長度均保持在10。

4.1 CPU占用率測試

為了驗證三種方法在挖掘數據點位置過程中的CPU占用率，在上述實驗環境中，依照實驗設定的參數，展開對比仿真，仿真結果如圖2所示。

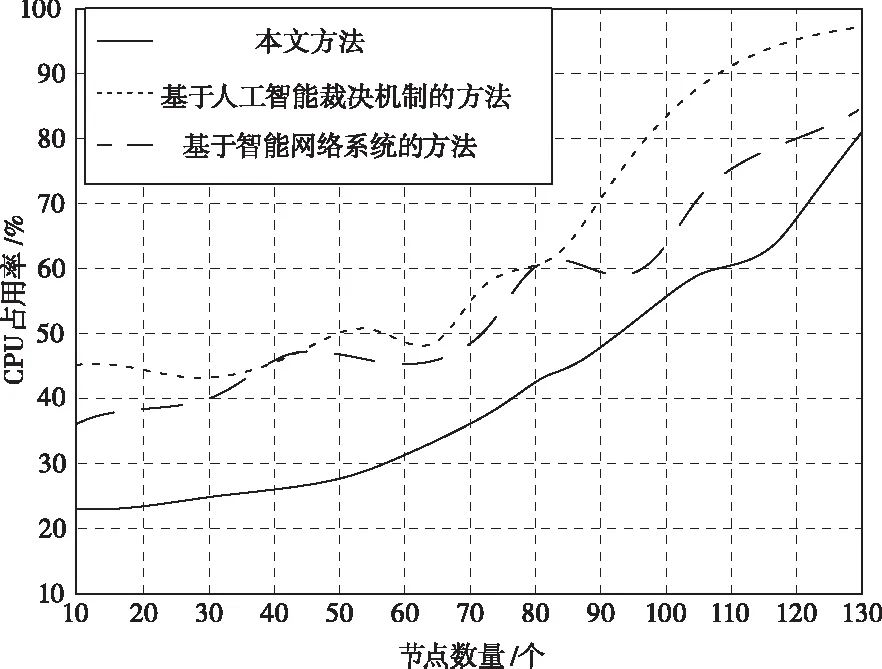
圖2 三種方法CPU占用率對比

從圖2中可以看出，不論節點數量怎樣變化，本文方法較其它兩種方法相比，均展現出了明顯的優勢，一直保持在較低的水平下，并且波動幅度也較其它兩種方法相比要小。這是由于本文方法引入了增量分類方法，快速處理各類數據巨大且復雜的數據，實現高效挖掘，同時，使算法整體保持在平穩的狀態下，避免出現較大的波動。

4.2 挖掘時延測試

隨著節點數量的不斷增加，挖掘時延也發生了改變。本文方法與其它兩種方法相比，在挖掘時延方面的測試結果如圖3所示。

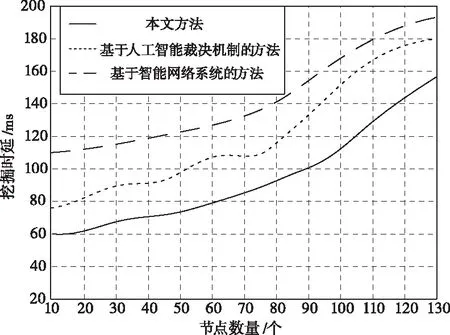
圖3 三種方法挖掘時延對比

從圖3中可以看出，雖然節點數量在不斷的增加，但是本文方法的挖掘時延一直比其它兩種方法要低，并且波動的幅度也較其它兩種方法相比要緩一些。這是由于本文方法在挖掘數據點位置的過程中，將挖掘的帶寬、數據集的存儲大小以及多種因素綜合考慮在內，在節點數量不斷增加的同時進行快速的運算，有效降低挖掘時延。

4.3 數據點位置信息熵

隨著挖掘得出節點位置數量不斷增加，為了驗證其位置結果是否存在有效信息和數據，通過信息熵指標判斷。信息熵能夠描述挖掘結果內信息量的大小，設定大于0.5的位置信息為挖掘有效數據。圖4為分別運用三種方法挖掘信息熵結果對比圖。

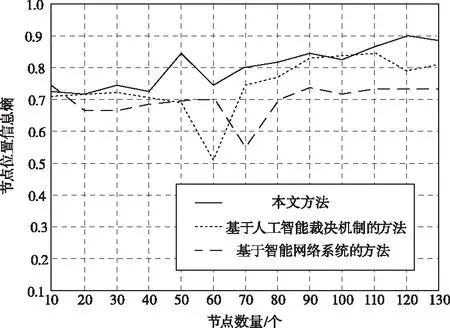
圖4 挖掘信息熵對比

從圖4中可以看出，三種方法挖掘結果均大于0.5，都符合要求，但是相對于文獻方法來說，本文方法的位置信息熵值更高、曲線更加平穩，沒有出現較大的波動。這是由于本文方法充分考慮到了數據點的屬性信息，只需要在計算過程中輸入與之對應的標簽信息即可，減少了計算步驟，因此可有效降低挖掘出現異常情況的概率。

4.4 可擴展性測試

可擴展性指的是當節點數量按照一定的比例增加時，計算此時的算法性能。可擴展性scaleup的計算公式如式(6)所示

scaleup(D，m)=t1*D/tm*m*D

(6)

式中，t1*DB表示1個節點在D中所花費的計算時間；tm*m*D表示當節點數量為m時，在規模大小為m*D的項目集上運行所花費的時間。

在評判過程中，當scaleup的值在0.65以上，說明該算法具有優秀的可擴展性。圖5為本文方法在支持度大小分別為5%、10%、15%的情況下，所得的可擴展性結果。

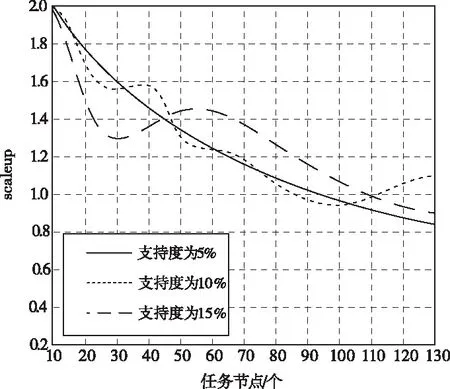
圖5 支持度不同的情況下本文方法可擴展性

從圖5中可以看出，本文方法在支持度不同的情況下，所得scaleup的計算結果均在0.65以上，說明本文方法具有優秀的可擴展性。

5 結論

本文通過并行FP-Growth算法與Map/Reduce并行編程模型的結合，使得FP-tree在挖掘迭代的過程中具有更為理想的效率。通過設置仿真，在CPU占用率、挖掘時延、信息熵方面與傳統方法展開對比，驗證了本文方法在挖掘時延較少的前提下實現了對數據點位置的高效率挖掘。最后在支持度不同的情況下對本文方法的可擴展性完成了實驗驗證，結果表明本文方法具有優秀的可擴展性。