遙感星座的效能分析與重構控制

白保存，馮孝輝

(1. 航天系統部裝備部項目管理中心，北京100094；2. 航天東方紅衛星有限公司，北京100094)

1 引言

遙感星座設計是一個反復迭代，對各種備選方案權衡取舍的過程，這就涉及到權衡取舍所采取的標準，這種標準的選取直接決定了星座設計結果能否滿足設計者的預期目標并發揮其既定的各項功能。因此，星座設計所面臨的首要問題是建立星座方案的品質指標評價體系，通過該體系的建立，確定星座方案權衡取舍的標準，且該標準應當充分挖掘反映星座系統本身和運行維持過程中的種種內在特性。在衛星星座設計研究領域，星座方案所能提供的系統能力是設計和方案評價過程中人們最為關心，認為最重要的品質指標。根據不同的任務需求，國內外現有的研究成果主要分為以覆蓋特性為核心的傳統評價指標、基于導航精度的評價指標、衛星網絡的連通性指標和路由策略、從星座實際運營角度提出的系統評價指標、功能復合型星座的評價指標、通用化的衛星星座系統構架描述和系統設計評價指標。

美國的GPS最早開展導航系統性能評估，繼承了無線電導航領域的部分用以評定精度的一般方法，并在此基礎上根據衛星導航系統本身的一些特點發展或修改了部分指標的定義，針對GPS、SPS和PS建立了一套比較完善的衛星導航系統性能評估體系。Karl Kovach等人對四大性能指標(精度、完好性、連續性和可用性)概念進行深入研究，在此基礎上給出了四大性能指標關系模型。Heng L等人研究了2009-2011年間GLONASS空間信號誤差的特性，結果表明GLONASS的長期穩定性良好，空間信號精度達1.5-4米。Oehler等人系統地提出了Galileo系統地完好性概念和相應的計算方法，奠定了Galileo的完好性研究基礎。呂志平介紹了GPS通過更換更為先進的導航衛星、取消選擇可用性、增加民用信號等措施后的衛星性能改進。陳金平在系統總結GPS廣域增強系統和局域增強系統的基本原理和方法上，針對廣域增強系統RAIM多故障問題，提出了基于漏檢概率的方差放大的可用性分析方法，基于多元假設故障容錯處理技術提出了在用戶定位域進行LAAS多參考站故障檢測和排除方法，提高了系統的可用性能。秘金鐘提出了基于聚類分析的相關距離法的QR奇偶檢校法的新型RAIM算法。

航天器編隊構形重構的最優沖量控制本質上屬于兩點邊值問題，應用哈密頓原理、母函數、正則變換以及Hamilton-Jacobi方程為兩點邊值問題提供了一種解法，該方法可應用于最優軌道交會，同樣可應用于構形重構。從本質上說，編隊捕獲也可視作一種特殊的構形重構，其研究都可用于一般性的構形重構控制。

此外，許多針對在重構的研究基于LQR理論，Lyapunov函數等關注于脈沖控制用于重構。而考慮離子發動機技術具有輕質量，高脈沖和長持續時間等優點，可以將其應用于編隊飛行重構操作。但是當前關于該應用方向的研究較少。Huntington和Rao將燃料最少消耗的四面體編隊重構轉化為多階段非線性最優控制問題，并采用高斯偽譜法求解。Garcia-Taberner和Masdemont將有限元方法應用于圓形限制性三體問題框架的Halo軌道編隊飛行重構任務中，顯示了該方法的有效性，但是他們所研究的重構時間相對于日地系統L點Halo軌道周期較短(8小時和24小時)，因此實際上所研究問題的本質還是時不變系統，而針對近地編隊飛行，重構時間相對于繞地周期往往較長，需要在數個軌道周期內完成，時不變系統方法并不直接適用于近地編隊飛行的重構問題。因此，需要研究適用于近地編隊飛行的重構優化方法。

Alfriend研究編隊飛行構型初始化和重構的混雜策略，并首次提出閉環自主控制回路；McInnes在繞飛構型歸一化描述的基礎上，提出了兩次脈沖速度增量實現繞飛的兩種方案：在一種分層控制結構下，通過兩種初始化方案的合理組合，可保證衛星群整體的初始化可在一個軌道周期內完成，從而降低了初始化誤差。Xu構造保Hamiltonian結構控制器用以維持編隊構型穩定。

國內的韓潮、鄧麗等人采用網格點仿真法對衛星星座的覆蓋性能進行了統計評估。徐敏等人應用視函數法和地心法建立了星座覆蓋性能評定的數值仿真方法，并對星座的對地覆蓋性能進行了數值仿真。劉會杰在其博士學位論文中對區域衛星定位系統衛星星座設計和星座系統性能評價的有關問題進行了研究。該文給出了兩種覆蓋性的定義，推導了相應的覆蓋判據，并對兩種覆蓋性定義的等價性進行了證明；深入研究了DOP因子的物理含義和性質，利用矩陣特征值法推導了DOP因子最小化條件，利用幾何效應矩陣證明了DOP因子對坐標變換的不變性，設計了基于m序列的組合計數算法對于DOP因子仿真計算，避免了矩陣求逆運算，從而選擇出合適的星座構型。

陳曉宇等人針對衛星系統總體設計方案科學評估和論證問題，根據遙感衛星的應用模式和任務完成要求，研究了面向任務的遙感衛星綜合能力評估技術，基于層次結構模型的特點和適用性，采用層次分析法建立衛星星座綜合性能評估指標體系，在此基礎上，通過靜態評估體系、動態評估體系和運行維持性能三方面對星座總體性能和效能指標進行全面分析。王小康提出了一種基于IP協議的衛星通信系統評估要求和評估方法，并進行了評估測試。李維國等人根據我國戰術衛星通訊系統的建立需求，提出了一種用模糊綜合評判方法評估戰術衛星通信系統的性能。

遙感星座通常對目標區域有一定的重訪時間要求，因此最大或平均重訪時間是其一個重要的品質評價指標，另一方面，衛星對地面的觀測分辨率直接影響觀測效果，它也應當作為星座的品質評價指標，觀測分辨率與光學相機物理屬性、衛星到待觀測點距離及待觀測點對衛星的最小可視仰角有關。

本文針對典型遙感星座的標稱效能和星座受損后的性能損失的進行了具體研究分析。針對遙感星座在受到小規模損壞或者大規模沖擊后的PDOP性能的具體損失，比較了受損前后的損失效果圖，并據此提供了遙感星座的具體衛星備份策略；針對定位星座的性能，以時間分辨率為參考依據，比較了受損前后星座的時間分辨率變化值；針對觀測星座的效能參數，分情況討論了受損衛星為內星座或者外星座時的時間分辨率和覆蓋時長變化情況。

2 遙感星座參數

遙感星座已經發射十余顆衛星，本節選取目前space-track網站已知的十五顆衛星中的十二顆作為有代表性衛星星座為例研究星座的整體特性。該星座衛星均為近地軌道衛星，軌道高度約為600km，偏心率很小，近似為圓軌道，保證了對全球中低緯度地區的均勻覆蓋。標稱軌道詳細參數如表1所示，表中列出了2019年9月21日零時衛星星座在J2000坐標系下的位置。地面采樣點以該星座的設計覆蓋區域中國東部地區為主要目標，采用十六個采樣點(表2)代表此區域。

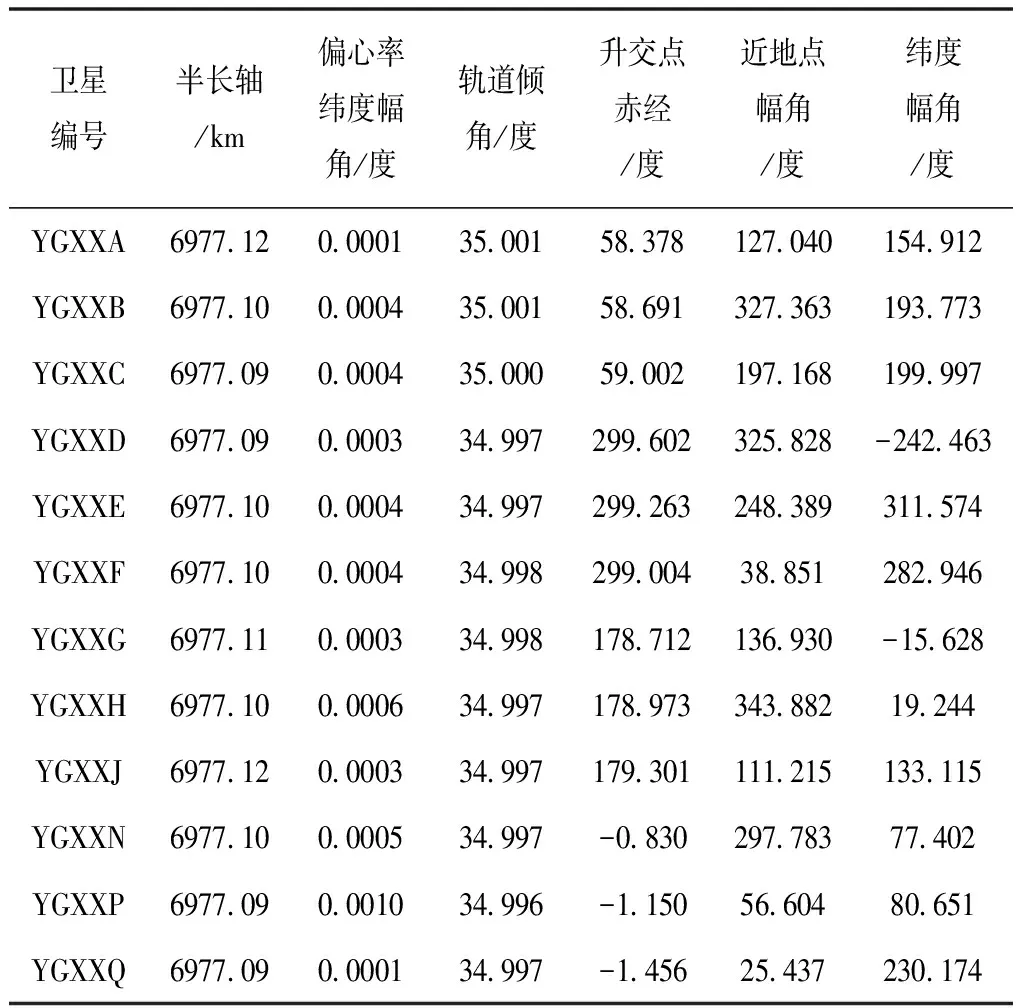
表1 遙感衛星星座構型參數

表2 地面采樣點位置

3 遙感星座的靜態性能指標

衛星載荷視場角為60°，仿真開始時間為2019年9月21日0時，對地面十六個目標點進行為期1天的仿真分析，初始時刻覆蓋效果圖如圖1所示。

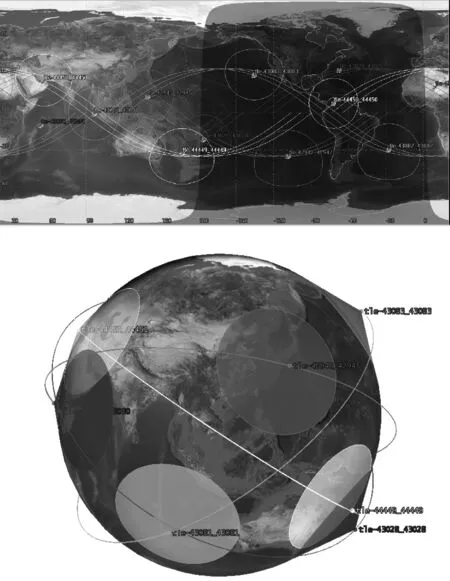
圖1 遙感星座覆蓋效果圖

參考前述的計算原理，設置權重值，，，均為1，計算遙感星座的靜態性能指標。位置精度衰減因子在仿真周期內對地面指定目標的平均值為8134，重定義的位置精度衰減因子值為1866，地面采樣距離在仿真周期內對地面指定目標的平均值為1749，覆蓋時間百分比cov在仿真周期內對地面指定目標的平均值為0481，通信容量期望值在仿真周期內對地面指定目標的平均值為0157，靜態性能綜合評價指標為43827。對比發現遙感星座對地面指定目標點的覆蓋性能較好，符合遙感星座設計的目標特性要求。

4 遙感星座的可用性模型

對遙感星座的可用性模型采用威布爾(Weibull)函數可靠性估算方法，衛星在運行周期中運行了時間(年)后正常運行的概率按下式估算

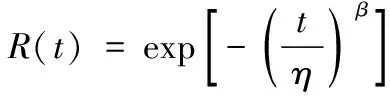
(1)

式中是與衛星設計壽命有關的一個時間常數；取為典型值16。已知衛星在運行=8年后的正常運行概率為=092，則有

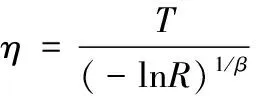
(2)

由式(2)可求得=377938，再由式(1)即可求得衛星運行年后的正常運行概率詳見表3。

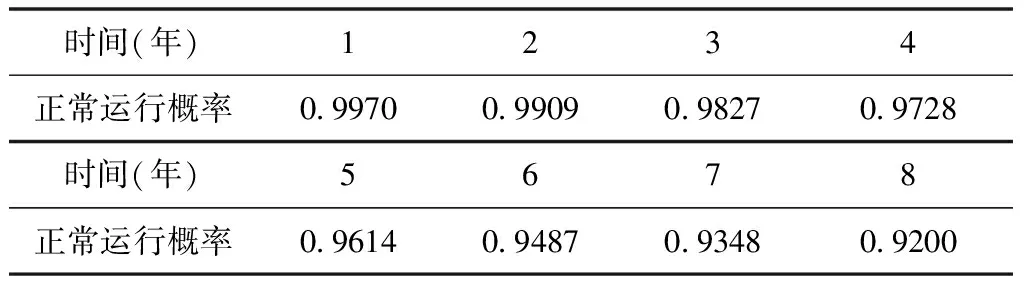
表3 衛星在不同時期的正常運行概率

令=12為星座中衛星總數，運行年后星座中失效衛星數目為，則隨變化的擬合圖如圖2所示。

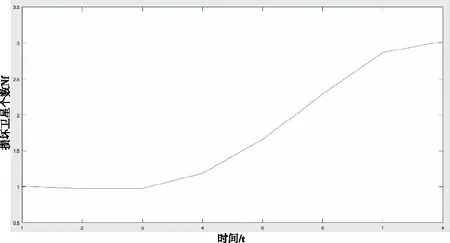
圖2 單星可用性模型圖

從概率的角度上講的取值范圍應為0到=12，星座中恰有顆失效衛星的概率是

()=(1-())×(())-

(3)

考慮到由于從遙感星座中選擇顆失效衛星有多種組合方式，設組合方式的數目為(對應損壞衛星數目不同的情況)，則應對式(3)作如下修正

()=×(1-())×(())-

(4)

取表3中衛星正常運行概率，初始時刻在軌衛星12個為例。隨時間推移，分別運行一年，四年，八年后還在軌運行的衛星個數與概率關系的分布圖如圖3所示。

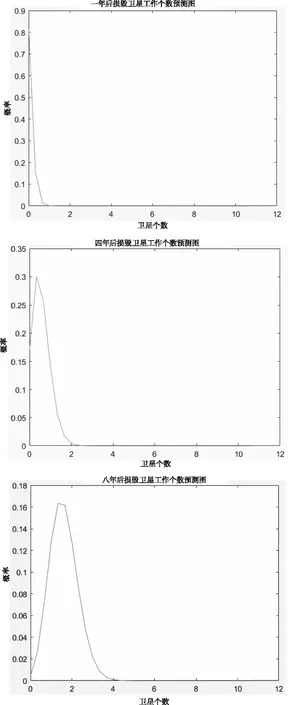
圖3 遙感星座星座可用性預測圖

由上圖可知工作一年后，遙感星座失效概率極小，可繼續完全狀態運行。四年后，遙感星座可能會有一顆衛星失效，由于星座構型設計的對稱性，單顆衛星失效無論哪一顆對星座整體性能的影響是一致的，均可以通過任何一顆的失效模型相對應。八年后，遙感星座可能會有兩顆衛星失效，分兩種情況討論，若兩顆失效衛星在同一軌道平面上，則受損星座在局部地區瞬時覆蓋區性能損失較大；若兩顆失效衛星在不同軌道平面上，將對星座整體性能產生影響。

5 利用遺傳算法重構受損星座

針對六個指標評價參數進行整個仿真周期內評價調用，根據遙感星座的使用需求，對不同評價指標賦予不同權重因子，得綜合評價因子為

=×(·+·

+·+·-·)

(5)

采用遺傳算法對該星座設計優化參數設置為種群數量為20×剩余衛星個數，遺傳代數設置為10×剩余衛星個數，代際偏差容忍極限值默認，容忍極限代數設置為10。

若一顆衛星受損，以未損傷衛星軌道根數為初始參數，令=0，其余權重因子均取1，仿真周期為一天，取相同，用遺傳算法優化一顆衛星損傷后剩余兩顆同軌面的兩顆衛星的緯度幅角和升交點赤經得綜合效能指標評價函數1=52451，升交點赤經分別為193624和452314，緯度幅角分別為253016和1916543。

若兩顆受損衛星在相同軌道平面，優化受損衛星軌道面的剩余一顆衛星和受損衛星相鄰軌道面的兩顆衛星的升交點赤經和緯度幅角，取相同權重因子作為輸入得2=56626，優化結果升交點赤經和緯度幅角分別為1761441，565813，290179和1931648，2350631，2182672。

若兩顆受損衛星在不同軌道平面，分別優化受損衛星軌道面的剩余兩顆衛星共四顆衛星的升交點赤經和緯度幅角，取相同權重因子作為輸入得3=53518。由以上優化過程知，星座受損情況不同，優化對象也應根據受損情況做出不同優化才能得到較好優化結果，盡可能恢復星座性能。

6 遙感星座的構型重構路徑優化

根據上節遺傳算法的優化結果，利用偽譜法構型重構路徑優化策略，實現由初始構型到目標構型的重構路徑求解。圖4給出編隊重構前后的初始軌道、目標軌道以及重構軌道；圖5給出重構過程中的小推力加速度時間歷程；圖6給出編隊軌道構型不變量在重構期間的時間歷程。

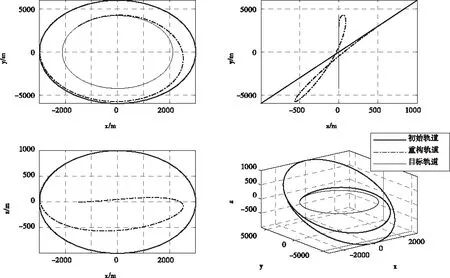
圖4 采用偽譜法，得到的重構前后軌跡以及重構路徑

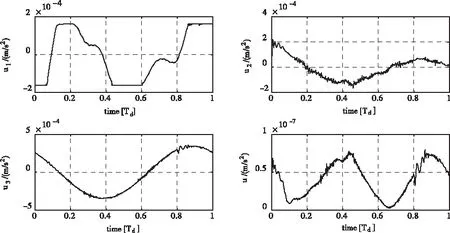
圖5 采用偽譜法，重構期間的小推力加速度時間歷程

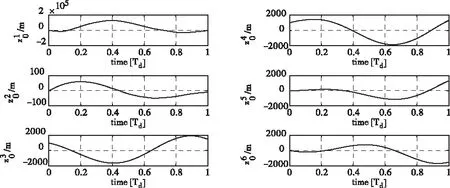
圖6 采用偽譜法，構型不變量z在重構期間的時間歷程

星座構型重構不同于編隊構型重構，初始軌道與目標軌道在徑向尺度上存在較大偏移，而線性相對運動方程-方程要求主星與從星相對距離尺度較小，此時將不再適用于星座間的軌道重構。因此，將星座構型轉移重構過程劃分為一定數量的編隊構型重構組合問題，設定相應的“虛擬主星”，將不同主星的相對軌道重構路徑進行拼接，從而實現大尺度星座構型重構。

考慮星座的主星與從星均位于近地無攝圓軌道的情況，星座構型重構步驟如下：首先確定初始構型，主星軌道傾角為從星與主星相對距離較近，組成衛星編隊，相對構型為，相對運動關系可線性化，-方程成立。假定從星目標軌道半長軸與星座主星相同，則存在一個“虛擬主星”軌道，使得從星目標軌道相對于“虛擬主星”存在小尺度的穩定相對構型，其相對運動關系符合-方程，此“虛擬主星”的軌道傾角為。該“虛擬主星”除軌道傾角外，其余軌道根數均與星座真實主星相同。接著，在地球慣性坐標系下，建立-1個“虛擬主星”軌道，半長軸與軌道周期與主星相同，軌道傾角分別為

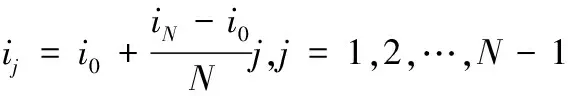
(6)

將在目標軌道中的相對構型通過坐標變換，分別求解出在各個“虛擬主星”相對軌道坐標系中的構型。最后，通過偽譜法優化，分別求解由構型-1到在一個軌道周期內的重構路徑，并將所有路徑進行拼接，從而實現大尺度星座構型重構。

將以初始主星為坐標原點，繪制軌道構型重構路徑，如圖7所示。值得一提的是，由于星座重構后的從星與主星不再構成穩定的相對構型，因此其運動軌跡存在漂移。

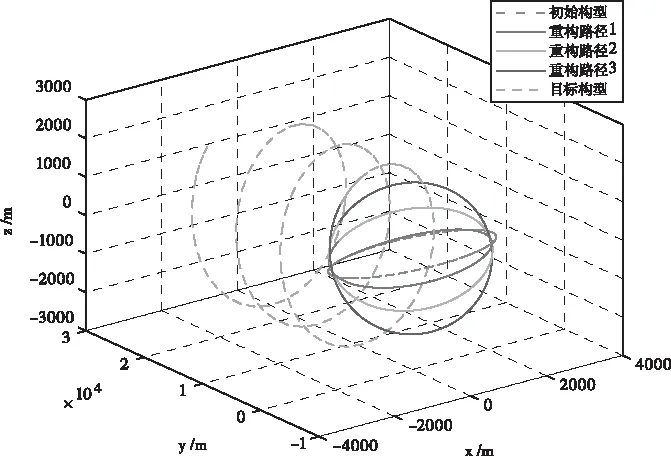
圖7 采用偽譜法，星座構型重構路徑

7 遙感星座的重構LQR跟蹤控制

以兩個航天器組成的編隊任務為例，主星運行于800km近地圓開普勒軌道，不考慮攝動等因素影響；重構前后的構型參數，即初始軌道和目標軌道的參數選取如下：=[1，0，1，1，0，0](構型中心位于沿跡向7處、構型半徑為335)和=[-1，0，0，2，2，0](構型中心位于沿跡向-7處、構型半徑為608)；重構周期為1個軌道周期=60524。采用基于多項式函數擬合的重構路徑優化方法，實現相對軌道由初始構型到目標構型的重構。設定轉移的初始誤差=[01，01，01，01，01，01]。控制時間為3個軌道周期(3×)，其中第一個軌道周期完成重構，接下來兩個軌道周期維持在新軌道上。，，三個參數分別取為如下的對角矩陣

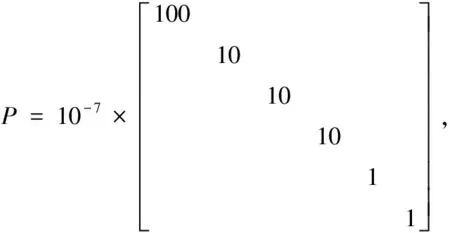
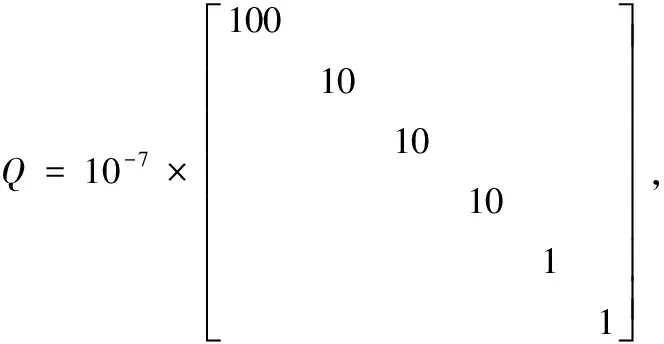
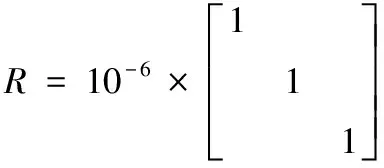
仿真結果如下：狀態量的變化如圖8所示(藍線表示實際狀態，紅線表示標稱狀態)。

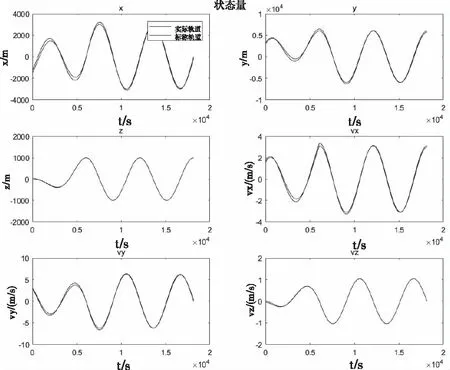
圖8 狀態量-時間曲線圖

狀態誤差的變化如圖9所示。

圖9 狀態誤差-時間曲線圖

控制量的變化如圖10所示。

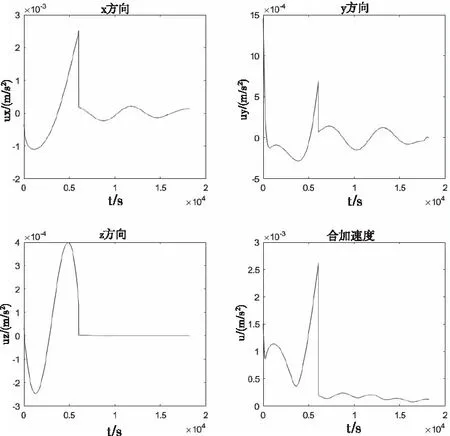
圖10 控制量-時間曲線

從仿真結果可以看出，跟蹤效果良好，誤差有收斂趨勢，控制量滿足要求，表明LQR跟蹤控制效果較好。

結合以上重構和控制看結果，重構過程中星座的效能如下圖所示。由圖可知，重構過程中，星座性能現時快速下降，最后提升至原星座性能的82%，重構過程大約需要3.5天，符合計劃時間。

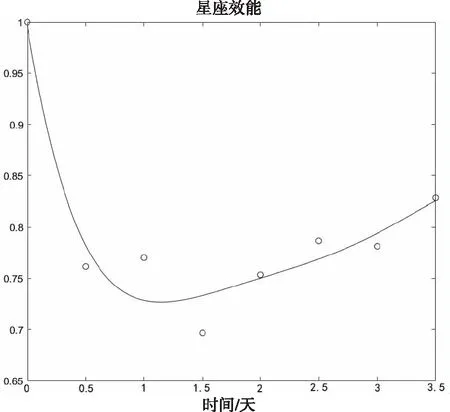
圖11 優化過程中星座效能隨時間變化圖

8 結論

本文基于最新的遙感衛星星座，建立了綜合指標評價函數分析其星座性能，并根據星座服務可用性的壽命預測模型分析其在軌服務故障特性。針對不同故障模式，分別分析了星座剩余性能，并選擇合理的星座重構優化策略對剩余星座進行優化重構。最后通過最優控制方法，求解重構路徑并采用LQR控制優化重構路徑，評估星座損壞前后和重構過程中星座的整體性能和重構方案的合理性。結果表明，本文提供的重構算法能夠顯著提升損壞后的星座整體性能。