低速移動機器人的同時跟蹤與避障研究

張雋賡，張?zhí)嵘坪Ａ粒Ｐ◇K

(武漢大學(xué)衛(wèi)星導(dǎo)航定位技術(shù)研究中心，湖北武漢 430079)

1 引言

隨著機器人技術(shù)的發(fā)展，低速移動機器人作為一種特殊的地面移動機器人，如掃地機器人[1]、自主導(dǎo)航農(nóng)業(yè)拖拉機[2]、建筑機器人[3]等，越來越多地影響著人們的生活。

為實現(xiàn)低速移動機器人自主導(dǎo)航，現(xiàn)有研究大多采用在全局路徑的基礎(chǔ)上進(jìn)行局部避障[1-3]的方式，上述導(dǎo)航方式無法對機器人導(dǎo)航過程的時間進(jìn)行規(guī)劃。軌跡跟蹤作為機器人的導(dǎo)航方式之一，能夠保證機器人在規(guī)定時間運動在指定的狀態(tài)附近。然而，移動機器人軌跡跟蹤誤差系統(tǒng)往往是一類耦合非線性系統(tǒng)，不滿足Brockett鎮(zhèn)定的必要條件[4]。因此，傳統(tǒng)的線性方法不能直接應(yīng)用于移動機器人系統(tǒng)。目前，解決輪式機器人軌跡跟蹤問題的方法[5-9]大多假設(shè)導(dǎo)航場景為全局已知，難以直接應(yīng)用于復(fù)雜多變的現(xiàn)實環(huán)境。經(jīng)典的避障方法[10-14]的主要思路是設(shè)計局部目標(biāo)點并在每個時刻尋找最優(yōu)航向，缺乏軌跡跟蹤方面的考慮。因此，能夠同時滿足軌跡跟蹤與避障的方法對機器人應(yīng)用必不可少。

文獻(xiàn)[15]針對軌跡跟蹤與避障兩種情形分別設(shè)計了兩種控制律，并根據(jù)機器人所處環(huán)境決定使用何種控制律。由于兩種控制律差異較大，因此在控制律切換過程中機器人會存在能量損失。文獻(xiàn)[16-17]設(shè)計了能夠同時進(jìn)行軌跡跟蹤與避障的控制律，但相應(yīng)的控制系統(tǒng)復(fù)雜度高，不易實現(xiàn)。文獻(xiàn)[3]使用動態(tài)窗口法(DWA)跟蹤由A*算法規(guī)劃的路徑點，但是這種做法無法預(yù)測機器人完成導(dǎo)航的時間，也沒有解決障礙物占據(jù)路徑點使得局部目標(biāo)點不可達(dá)的問題。文獻(xiàn)[18]設(shè)計的基于速度空間的控制律VSTTM (velocity space based concurrent obstacle avoidance and trajectory tracking method)能夠使機器人在跟蹤參考軌跡的同時考慮避障，但基于VSTTM的機器人低速行駛時無法躲避直線軌跡上的障礙物，這限制了低速移動機器人的工作場景。

本文對VSTTM進(jìn)行改進(jìn)。首先分析基于速度空間的同時跟蹤與避障方法VSTTM的缺陷問題。針對VSTTM的缺陷改進(jìn)了原目標(biāo)函數(shù)，并設(shè)計了跟蹤狀態(tài)與避障狀態(tài)的切換機制。通過Ubuntu 16.04+ROS Kinetic+Gazebo 7.0仿真比較改進(jìn)前后的實驗結(jié)果。相較于其它同時跟蹤與避障的方法，改進(jìn)算法保留VSTTM算法的優(yōu)勢：結(jié)構(gòu)簡單、軌跡跟蹤效果明顯、避障方式高效。此外，有效解決VSTTM算法的固有避障缺陷，跟蹤與避障的狀態(tài)切換過程考慮了機器人狀態(tài)的漸變，能量損失極小，相同速度條件下?lián)碛懈叩母櫨取?/p>

2 基于速度空間的同步軌跡跟蹤與避障方法(VSTTM)

同時適用于軌跡跟蹤和避障的方法一般分為兩類：根據(jù)是否應(yīng)該避障設(shè)計兩種不同的控制律[15]，或設(shè)計一種控制律[16-18]同時解決避障與跟蹤問題。下面將分析同步軌跡跟蹤與避障方法VSTTM[18]的設(shè)計原理及存在的不足。

2.1 構(gòu)建速度空間

首先構(gòu)建非完整約束的輪式移動機器人軌跡跟蹤誤差方程。盡管不同低速移動機器人擁有不同的運動執(zhí)行機構(gòu)，但它們擁有共同的可控制變量：前進(jìn)速度v與轉(zhuǎn)彎速度ω。因此本文的機器人運動學(xué)模型建立如式(1)-(2)。

圖1中，當(dāng)前時刻t機器人在全局坐標(biāo)系XgOgYg的位姿表示為q(t)=[xt，yt，θt]T，相應(yīng)的速度向量表示為u(t)=[vt，ωt]T；時刻t對應(yīng)的參考位姿記為qr(t)=[xr(t)，yr(t)，θr(t)]T，對應(yīng)的參考速度記為ur(t)=[vr(t)，ωr(t)]T。運動學(xué)方程如式(1)所示

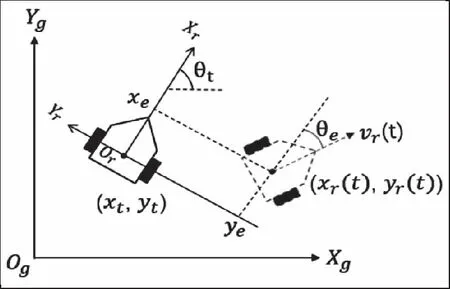
圖1 移動機器人軌跡跟蹤示意圖

(1)

機器人局部坐標(biāo)系：以機器人中心or為原點，xr軸與機器人航向相同，yr軸由xr軸逆時針方向旋轉(zhuǎn)90°得到。跟蹤誤差方程如式(2)所示

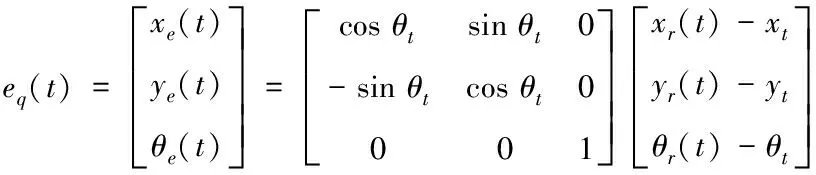
(2)

文獻(xiàn)[1]、[15]的測試結(jié)果表明：基于式(1)-(2)的簡化運動學(xué)模型所設(shè)計的控制算法，應(yīng)用在低速移動機器人上能夠表現(xiàn)出不錯的控制效果。因此本文的導(dǎo)航算法將在該運動學(xué)模型的基礎(chǔ)上構(gòu)建。

構(gòu)建速度空間U[13]：設(shè)機器人能夠達(dá)到的線速度最大值為vmax，最小值為vmin，角速度最大值為ωmax，得到機器人所有可能的速度范圍構(gòu)成一個速度空間Us

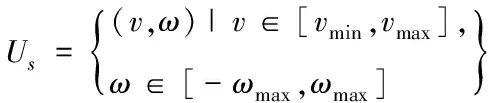
(3)

(4)

速度空間U(控制集)即兩個速度空間Us和Ud的交集，滿足式(5)

U={(vi，ωi)|(vi，ωi)∈Ud∩Us}

(5)

(6)

2.2 VSTTM避障缺陷分析

基于速度空間的同時避障與軌跡跟蹤方法(VSTTM)[18]同樣是基于速度空間的導(dǎo)航算法。對所有符合式(5)的控制集U，丟棄預(yù)測周期[t，t+Tf]內(nèi)可能與障礙物碰撞的預(yù)測軌跡，從剩余可通行解中尋找最優(yōu)控制量u*滿足式(7)

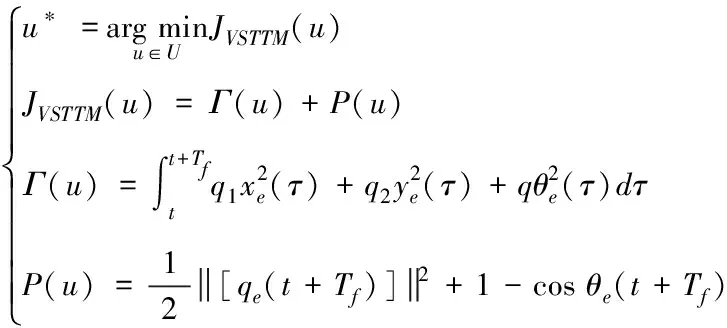
(7)

式(7)中，Γ(u)評價控制量u在周期[t，t+Tf]內(nèi)的預(yù)測軌跡與參考軌跡之間的偏差，P(u)評價末端狀態(tài)q(t+Tf)與參考軌跡末端狀態(tài)qr(t+Tf)的偏差。

圖2 VSTTM跟蹤直線軌跡情況

VSTTM存在如下缺陷：機器人在VSTTM控制下跟蹤勻速直線軌跡，且參考速度vr較小時，將做減速直線運動。且當(dāng)速度降低到一定程度后將發(fā)生避障失敗的情況。圖2展示了上述缺陷的過程。圖2(a)表示機器人的預(yù)測軌跡受障礙物干擾初期的狀態(tài)，此時機器人將做減速直線運動。隨著時間推移，機器人從圖2(a)代表的狀態(tài)持續(xù)減速到圖2(b)狀態(tài)：由于速度減小，相應(yīng)的預(yù)測軌跡探測范圍寬度s′ 與障礙物大小相等。由于圖2(b)狀態(tài)下機器人的預(yù)測軌跡都不能成功避障，此處將該狀態(tài)視為避障失敗狀態(tài)。

下面將分兩步證明上述缺陷：1、證明預(yù)測軌跡受障礙物干擾初期(圖2(a))，機器人做減速直線運動；2、通過證明圖2(b)狀態(tài)時機器人仍做減速直線運動，說明機器人從圖2(a)狀態(tài)持續(xù)減速到圖2(b)代表的狀態(tài)，進(jìn)而導(dǎo)致避障失敗結(jié)果。

首先，設(shè)當(dāng)前時刻(t=0)機器人位姿為q0=[x0，y0，θ0]T，相應(yīng)的參考軌跡位姿為qr0=[xr0，yr0，θr0]T。在預(yù)測周期t∈[0，Tf]內(nèi)，參考軌跡以速度vr做直線運動，參考軌跡的坐標(biāo)(xr(t)，yr(t))由式(8)決定

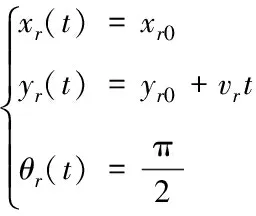
(8)

假設(shè)初始狀態(tài)(t=0)機器人處于跟蹤狀態(tài)，即跟蹤誤差較小，有

(9)

在預(yù)測周期t∈[0，Tf]內(nèi)，任意預(yù)測軌跡x(t)、y(t)為圓上的一段圓弧，滿足式(10)

(10)

VSTTM的尋優(yōu)過程由式(7)可簡寫為式(11)

JVSTTM(u)=(u)+(w)

(11)

為簡化計算，同時也考慮到實際測試中參數(shù)q1與q2相近時算法軌跡跟蹤效果最好，此處取q1=q2

(12)

F(u，t)=[xr(t)-x(t)]2+[yr(t)-y(t)]2

(13)

為獲取最優(yōu)控制量u*，分別考慮使R(ω)和Z(u)最小的控制量u。

首先分析使R(ω)最小的u。由式(12)可知，θe在定義域內(nèi)趨近0時，R(ω)減小。θe隨角速度絕對值|ω|減小而減小，且在ω=0取得最小值0。因此ω=0為R(ω)最小的最優(yōu)解。

接著分析u對Z(u)的影響。使Δx=xr0-x0，Δy=yr0-y0。將式(8)-(10)代入式(13)：

F(u，t)=△x2+△y2+(vrt)2+2f(u，t)

(14)

(15)

由式(14)可知F(u，t)的可控變量僅有線速度v與角速度ω，即求最優(yōu)速度u*僅需要考慮f(u，t)的函數(shù)圖像。取vr=0.3m/s，t=Tf=2s，將式(15)函數(shù)f(u，2)畫成圖像。

圖3 f(u，2)函數(shù)圖像

取t=Tf/2=1s時，f(u，1)與f(u，2)的函數(shù)圖像形狀相似，都在ω=0附近取到最小值。但f(u，1)的數(shù)值比f(u，2)大約減小0.38倍，f(u，0.5)的數(shù)值比f(u，2)小3個數(shù)量級。因此t較大時對f(u，t)的數(shù)值影響較大。由于障礙物的存在，最優(yōu)控制量只能取比vr更小的、可通行的線速度。綜上可知，預(yù)測軌跡受障礙物干擾初期，VSTTM控制下機器人必定做減速直線運動。

下面證明圖2(b)狀態(tài)時機器人仍做減速直線運動。圖2(b)中探測范圍s′≈robs=0.15m，v′≈0.21m/s。計算機器人減速到v′ 相比參考軌跡點落后的距離Δy0≈0.027m。將Δy0、v′ 代入式(15)后畫出f(u，t)的函數(shù)圖像仍與圖3相似：t較大時f(u，t)在ω=0附近取到最小值，命題得證。

3 VSTTM改進(jìn)算法

由1.2小節(jié)內(nèi)容可知，即使將預(yù)測周期Tf擴大到預(yù)測軌跡范圍覆蓋障礙物大小，也不能保證VSTTM算法能夠避障成功。因此限制機器人避障時的速度是一個有效的解決方法。本文提出了對VSTTM進(jìn)行改進(jìn)： 在速度空間的基礎(chǔ)上，從目標(biāo)函數(shù)入手優(yōu)化避障過程，并通過調(diào)整目標(biāo)函數(shù)的權(quán)重更好兼顧避障效果與跟蹤效果。

3.1 評價與優(yōu)化

(16)

(17)

評價函數(shù)T(u)衡量在周期[t，t+Tf]內(nèi)軌跡與參考軌跡之間的跟蹤誤差，在軌跡跟蹤效果評估中起主要作用

(18)

式中xe，ye，θe由式(1)-(2)得到，q1，q2，q3為相應(yīng)的權(quán)重系數(shù)。

根據(jù)文獻(xiàn)[18]設(shè)計終端狀態(tài)懲罰項P(u)，抑制機器人跟蹤過程出現(xiàn)震蕩現(xiàn)象：

(19)

設(shè)計評估機器人與障礙物之間距離的評價函數(shù)C(u)，且機器人越遠(yuǎn)離障礙物該項越小：

(20)

Dobs(t)為t時刻障礙物邊緣到機器人中心的最小距離，rrob為機器人的半徑，Δ為障礙物定位誤差的上界。

速度評價函數(shù)V(u)調(diào)整機器人避障過程的線速度v(t)。該項抑制目標(biāo)函數(shù)在滿足式(20)后選擇較小速度值。

V(u)=|v(t)-vr(t)|

(21)

3.2 跟蹤與避障的切換

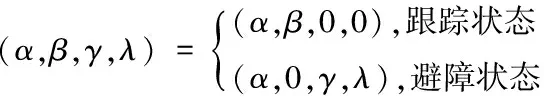
(22)

圖4 跟蹤與避障狀態(tài)的判斷示意圖

本文提出的VSTTM改進(jìn)方法將妨礙軌跡跟蹤的障礙物視為擾動。根據(jù)控制系統(tǒng)穩(wěn)定性定義，控制系統(tǒng)的穩(wěn)定性由系統(tǒng)本身決定，即外界干擾消失后系統(tǒng)回到平衡狀態(tài)的能力。由于算法在避障狀態(tài)時受到障礙物的持續(xù)干擾，不存在討論穩(wěn)定性的場合。改進(jìn)算法在跟蹤狀態(tài)時的參數(shù)與VSTTM完全相同，兩者的穩(wěn)定性有等效關(guān)系。VSTTM的原文獻(xiàn)[18]已對該算法穩(wěn)定性進(jìn)行證明。又因為兩種狀態(tài)的切換是在速度空間的約束下進(jìn)行，切換過程保持平穩(wěn)運動。因此改進(jìn)算法的穩(wěn)定性得到保證。

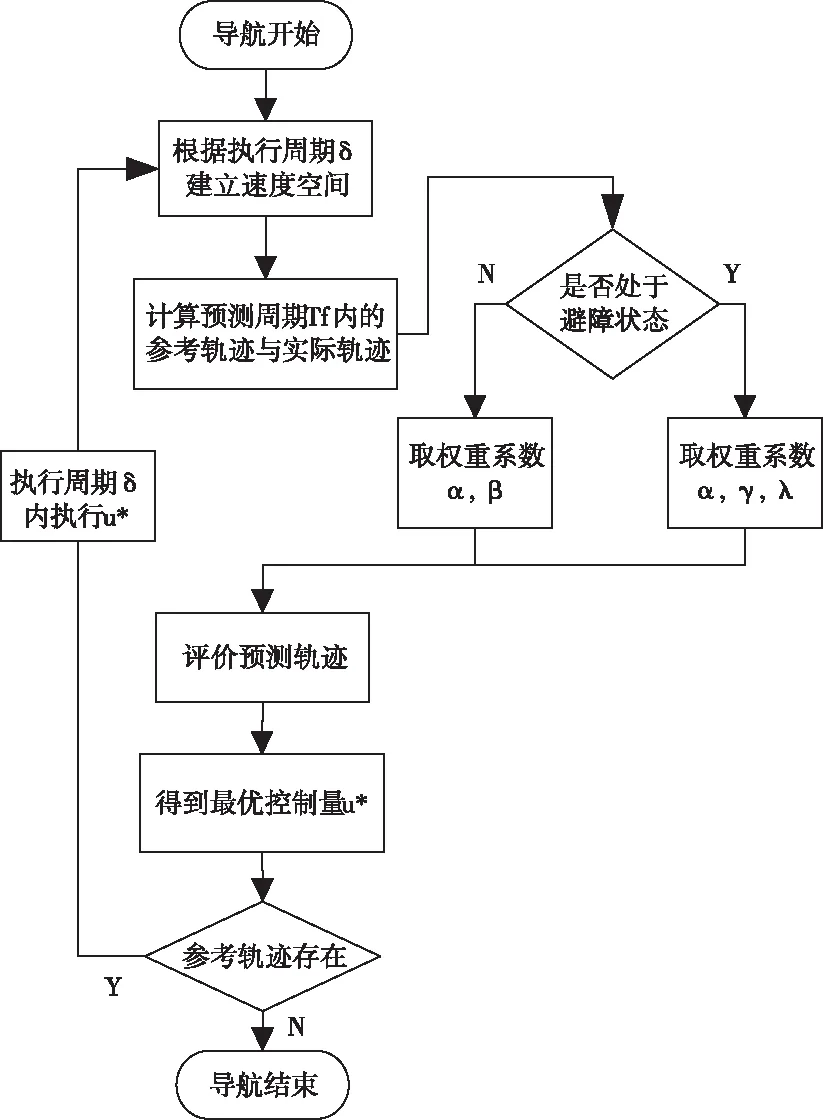
圖5 改進(jìn)的VSTTM流程圖

基于上述分析，VSTTM改進(jìn)算法實現(xiàn)流程總結(jié)如下：

輸入：機器人當(dāng)前時刻t的狀態(tài)q(t)=[xt，yt，θt]T和相應(yīng)速度u(t)=[vt，ωt]T，同一時刻的參考軌跡qr(t)=[xr(t)，yr(t)，θr(t)]T，對應(yīng)的參考速度記為ur(t)=[vr(t)，ωr(t)]T。傳感器數(shù)據(jù)和環(huán)境地圖。

輸出：最優(yōu)控制量u*。

算法流程如圖5所示：VSTTM改進(jìn)算法的一次迭代周期為執(zhí)行周期δ。在一次迭代周期內(nèi)，首先根據(jù)輸入評估預(yù)測周期Tf內(nèi)預(yù)測軌跡的優(yōu)劣并輸出u*。最后將輸出u*作為命令送予機器人執(zhí)行，完成一次迭代。當(dāng)參考軌跡到達(dá)終點，則導(dǎo)航過程結(jié)束。

4 仿真測試分析

為驗證改進(jìn)算法的有效性，本文在Ubuntu16.04+ROS Kinetic+Gazebo7.0環(huán)境下與VSTTM算法[18]進(jìn)行對比。Gazebo是一個常與ROS系統(tǒng)搭配使用的帶有物理引擎的開源機器人仿真工具，在模擬無人機和傳感器[20]、競賽[21]等領(lǐng)域均被廣泛應(yīng)用與認(rèn)可。測試的機器人仿真模型來自Wikipedia公司的turtlebot3-burger機器人的開源模型。

圖6 實驗測試仿真環(huán)境

4.1 VSTTM避障性能測試

該測試驗證VSTTM在應(yīng)對直線軌跡時表現(xiàn)出的缺陷。測試場景為寬6m的狹長通道，障礙物正中心坐落于坐標(biāo)(0，0)上。機器人初始位姿為q(0)=[0(m)，-8(m)，90°]T，速度矢量u(0)=[0，0]T。參考軌跡是以(0，-8)為起點，終點為(0，8)，速度為vr的勻速直線軌跡(圖8、9中紅色星型標(biāo)記)。根據(jù)文獻(xiàn)[18]中的圓形軌跡跟蹤進(jìn)行測試，并在算法穩(wěn)定的情況下取VSTTM參數(shù)q1，q2，q3，對多組參數(shù)和參考速度vr在相同場景下測試，觀察機器人避障效果。

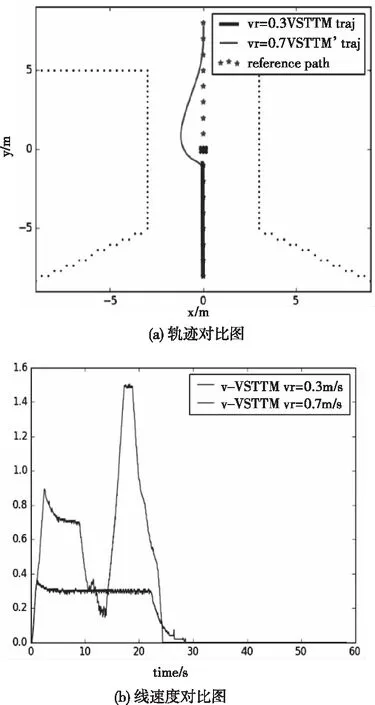
圖7 vr 分別為0.3與0.7時機器人導(dǎo)航情況

圖7表示參數(shù)為q1=q2=3，q3=0.5，vr分別取0.3m/s和0.7m/s情況下機器人的導(dǎo)航情況。圖8(a)中紅色軌跡為vr=0.7m/s機器人的軌跡，藍(lán)色軌跡為vr=0.3m/s的軌跡。結(jié)合圖8(b)的速度曲線，可以觀察到機器人在預(yù)測軌跡受障礙物干擾初期都開始減小速度。不同的是，vr=0.7m/s條件下機器人線速度減小到一定程度后開始避障，而在vr=0.3m/s的條件下機器人線速度直接減小到0。

表1 VSTTM避障情況一覽表

表1展示了不同算法參數(shù)與參考速度vr情況下機器人的避障情況：橫排表示vr具體數(shù)值，豎排表示不同的算法參數(shù)，√和×表示避障的成功或失敗。如，表格左上第一個×表示機器人在q1=q2=3，q3=0.5和vr=0.3m/s條件下避障失敗。

參數(shù)q1，q2，q3的調(diào)整導(dǎo)致不同避障結(jié)果的原因為：q1調(diào)大表明算法更看重前向距離偏差，對前向距離變化更為敏感，因此更容易避障。q2調(diào)大同理。但是q1與q2數(shù)值相差過大則不能保證算法的軌跡跟蹤效果。但無論如何調(diào)整，VSTTM仍然無法滿足turtlebot3-burger機器人(最大線速度0.3m/s)的避障需求。

4.2 改進(jìn)的VSTTM避障性能測試

該測試對VSTTM與改進(jìn)的VSTTM算法在同等條件(參考速度vr分別取0.3m/s和0.7m/s)下進(jìn)行避障表現(xiàn)的對比。VSTTM改進(jìn)算法參數(shù)q1，q2，q3與VSTTM相同，另取α=1，β=1，γ=3，λ=2。將相同條件下的VSTTM和改進(jìn)后的軌跡進(jìn)行比較，如圖8(a)-(b)所示(圖中改進(jìn)算法使用VSTTM′ 表示)。圖中黃色軌跡表示改進(jìn)算法VSTTM′ 的軌跡，藍(lán)色軌跡表示VSTTM軌跡。表2為VSTTM與改進(jìn)算法同時成功避障(vr=0.7m/s)過程中的跟蹤誤差最大值的對比情況。

圖8 VSTTM與VSTTM′ 軌跡對比

表2 VSTTM與改進(jìn)算法跟蹤誤差最大值對比表

通過比較得出結(jié)論：

1) 改進(jìn)算法在低速(vr=0.3m/s)情況能夠成功避障，成功克服VSTTM算法的避障缺陷；

2) 在速度較大、與VSTTM算法同樣成功避障的情況下，改進(jìn)算法的跟蹤誤差更小。

5 結(jié)論

針對移動機器人對已有軌跡的跟蹤過程探測到未知障礙物的避障問題，本文針對基于速度空間的同時避障與跟蹤方法VSTTM的避障缺陷進(jìn)行改進(jìn)，設(shè)計了衡量跟蹤誤差和遠(yuǎn)離障礙物程度的目標(biāo)函數(shù)。并根據(jù)機器人所處環(huán)境設(shè)計了跟蹤狀態(tài)與避障狀態(tài)的切換機制。仿真測試表明，與原方法相比，改進(jìn)后的VSTTM不僅解決跟蹤直線軌跡時的避障缺陷，在同樣成功避障的情況下?lián)碛懈玫母櫨取?/p>