執(zhí)行器飽和下機(jī)械臂有限時(shí)間控制
范云鵬,樊春霞
(南京郵電大學(xué)自動(dòng)化學(xué)院、人工智能學(xué)院,江蘇 南京 210023)
1 引言
如今,機(jī)器臂在各種應(yīng)用中變得越來(lái)越普遍,但由于其關(guān)節(jié)內(nèi)部結(jié)構(gòu)的復(fù)雜性及工作環(huán)境的不確定性,導(dǎo)致機(jī)械臂是一個(gè)典型的非線性、強(qiáng)耦合、時(shí)變不確定的系統(tǒng)[1][2]。在機(jī)械臂帶有負(fù)載時(shí)主要問(wèn)題是模型不確定性和外部擾動(dòng),為了解決模型不確定和外部擾動(dòng),提出很多控制策略,例如自適應(yīng)控制、魯棒控制、滑模控制、模糊控制及神經(jīng)網(wǎng)絡(luò)控制。
由于機(jī)械臂是一個(gè)典型的非線性系統(tǒng),滑模控制是運(yùn)用于機(jī)械臂系統(tǒng)控制中最為廣泛的一種。文獻(xiàn)[3]定義了機(jī)器人的PID型滑模面,設(shè)計(jì)了非線性滑模控制器,實(shí)現(xiàn)了機(jī)器人的主動(dòng)減振控制。文獻(xiàn)[4]提出了一種新的自適應(yīng)滑模控制器,用于機(jī)器人穩(wěn)定跟蹤控制。文獻(xiàn)[5]提出了一種使用自適應(yīng)積分滑模控制和時(shí)延估計(jì)的機(jī)器人機(jī)械手自適應(yīng)魯棒控制器,所提出的控制器具有很強(qiáng)魯棒性,無(wú)顫動(dòng)并且精度很高。
文獻(xiàn)[3-5]保證了機(jī)械臂跟蹤誤差的漸近穩(wěn)定性,這是一種表征時(shí)間無(wú)窮大時(shí)的穩(wěn)定性,然而實(shí)際的物理系統(tǒng)都是有時(shí)間限制的,需要研究系統(tǒng)的有限時(shí)間穩(wěn)定性[6,7]。文獻(xiàn)[6]采用自適應(yīng)快速終端滑模方法實(shí)現(xiàn)了剛性航天器的有限時(shí)間跟蹤控制,但終端滑模面存在奇異性問(wèn)題。文獻(xiàn)[7]針對(duì)存在執(zhí)行器故障和未知外部干擾的二階非線性系統(tǒng),提出了自適應(yīng)非奇異快速終端滑模(NFTSM)控制,該控制器可以消除與常規(guī)終端滑模控制有關(guān)的奇異性問(wèn)題。
在實(shí)際運(yùn)行過(guò)程中,當(dāng)控制輸入超出了執(zhí)行器輸出的上下限時(shí),“飽和”就產(chǎn)生了,這不僅會(huì)導(dǎo)致控制性能降低,甚至導(dǎo)致系統(tǒng)不穩(wěn)定[8]。由于機(jī)械臂快速瞬時(shí)響應(yīng)需要較大力矩,在機(jī)械臂的有限時(shí)間控制中就可能存在執(zhí)行器飽和問(wèn)題。文獻(xiàn)[9]提出適用于執(zhí)行器飽和的非線性機(jī)器人系統(tǒng)動(dòng)態(tài)抗飽和優(yōu)化,利用比例積分(PI)控制器,把其中的重力項(xiàng)通過(guò)非線性補(bǔ)償技術(shù)消除。文獻(xiàn)[10]提出了一種基于滑模控制方法的自適應(yīng)反升起控制策略,自適應(yīng)更新律用于估計(jì)不確定性的上限和執(zhí)行器飽和度的最小值。文獻(xiàn)[11]考慮輸入飽和誤差約束,實(shí)現(xiàn)了無(wú)人水面艦艇的自適應(yīng)容錯(cuò)跟蹤控制。文獻(xiàn)[9-11]研究了系統(tǒng)的飽和控制下問(wèn)題,實(shí)現(xiàn)了漸近穩(wěn)定,沒(méi)有涉及到有限時(shí)間穩(wěn)定。
機(jī)械臂是一個(gè)復(fù)雜系統(tǒng),很難用精確的模型來(lái)描述,往往用不確定模型描述。解決不確定性的有效工具之一是神經(jīng)網(wǎng)絡(luò),它可以近似任意非線性函數(shù)。文獻(xiàn)[12]考慮到當(dāng)機(jī)械手捕獲未知有效載荷時(shí)可能存在的模型不確定性,使用徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)(RBFNN)估計(jì)空間機(jī)械手模型中的不確定性。文獻(xiàn)[13]提出了一種基于NN的自適應(yīng)終端滑模控制器,用于空間機(jī)械臂的軌跡跟蹤。文獻(xiàn)[14]提出了一種應(yīng)用于SCARA機(jī)器人的非線性動(dòng)力學(xué)的多輸入多輸出自適應(yīng)神經(jīng)PID控制器。文獻(xiàn)[12-14]研究了機(jī)械臂模型不確定性時(shí)控制器的設(shè)計(jì)方案,但是沒(méi)有考慮執(zhí)行器飽和對(duì)系統(tǒng)穩(wěn)定性的影響。
綜上所述,研究及機(jī)械臂跟蹤控制問(wèn)題時(shí),不僅需要考慮有限時(shí)間穩(wěn)定,而且需要考慮模型不確定性以及執(zhí)行器飽和對(duì)跟蹤穩(wěn)定性的影響。鑒于此,本文的主要工作如下:
考慮機(jī)械臂模型不確定性以及受到外界擾動(dòng)時(shí)會(huì)嚴(yán)重影響機(jī)械臂穩(wěn)定性,提出了一種有限時(shí)間跟蹤控制器,實(shí)現(xiàn)了抗飽和控制。利用自適應(yīng)RBFNN網(wǎng)絡(luò)逼近模型不確定性以及外界擾動(dòng);設(shè)計(jì)飽和因子的自適應(yīng)律以補(bǔ)償執(zhí)行器飽和;提出快速終端滑模控制器,實(shí)現(xiàn)機(jī)械臂的有限時(shí)間跟蹤。
2 機(jī)械臂模型
包含干擾項(xiàng)的機(jī)械臂動(dòng)力學(xué)方程可表示為[15]

(1)
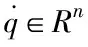
由于執(zhí)行器飽和會(huì)影響系統(tǒng)的穩(wěn)定性[8,9],因此這里考慮執(zhí)行飽和時(shí),研究機(jī)械臂跟蹤給定軌跡的控制器設(shè)計(jì)問(wèn)題。此時(shí),機(jī)械臂各個(gè)關(guān)節(jié)的輸入力矩可以表示為

(2)
τ為所需的控制力矩,τmax為已知輸入所需力矩τ的上界,sign(τ)=(sign(τ1),sign(τ2) ,…,sign(τn))T表示每個(gè)關(guān)節(jié)輸入力矩的符號(hào)函數(shù)。
引入飽和因子描述(2)所表示的飽和函數(shù)
sat(τ)=ω(τ)τ
(3)
其中ω(τ)=diag{ω1(τ1),…,ωn(τn)}表示執(zhí)行器的飽和特性
從ω(τ)的定義可以得到其滿足如下限制
0<φ≤ω(τ)≤1
(4)
其中φ是飽和因子ω(τ)的下界,是一個(gè)未知常數(shù)。
由于機(jī)械臂的動(dòng)力學(xué)模型中存在很多不確定性因素[12,13],因此無(wú)法精確給出式(1)中的慣性矩陣、哥氏力和離心力、重力項(xiàng),更是無(wú)法準(zhǔn)確確定外界擾動(dòng)。

假設(shè)1:期望軌跡qd∈Rn是一個(gè)二次連續(xù)可微的函數(shù)。
證明機(jī)械臂有限時(shí)間跟蹤給定軌跡時(shí),將用到如下引理。
引理1[16]:具有有限時(shí)間收斂性的擴(kuò)展Lyapunov描述為
(5)
其中?t>t0,V(xt0)≥0。對(duì)于任意t0,收斂時(shí)間為

(6)
其中λ1>0,λ2>0和0 本文采用自適應(yīng)方式逼近飽和因子下界φ的倒數(shù),利用神經(jīng)網(wǎng)絡(luò)逼近機(jī)械臂跟蹤給定軌跡過(guò)程中的非線性項(xiàng)以及外界擾動(dòng),采用終端快速滑模控制器使得機(jī)械臂能夠在有限的時(shí)間內(nèi)跟蹤給定軌跡。 定義系統(tǒng)跟蹤誤差及其導(dǎo)數(shù)為 (7) 則由(1)和(7)可得 =ω(τ)τ+f (8) 其中f為機(jī)械臂軌跡跟蹤過(guò)程中的未知非線性函數(shù) (9) 為了避免滑模控制中的奇異問(wèn)題[17],采用如下NFTSM滑模面 (10) 其中1/2 β=diag{β1,…,βn}(βi>0),i=1,2…n。 將滑模面(10)對(duì)時(shí)間求導(dǎo),然后將式(8)代入可得 (ω(τ)τ+f) (11) 控制律可設(shè)計(jì)為 (12) (13) 滑模控制系統(tǒng)利用切換控制律保證系統(tǒng)的狀態(tài)不離開(kāi)滑模面,傳統(tǒng)切換控制采用不連續(xù)控制項(xiàng)K·sign(s),會(huì)導(dǎo)致控制輸入信號(hào)產(chǎn)生抖振。為了保證控制律為連續(xù)函數(shù),可以使系統(tǒng)魯棒性增強(qiáng),降低滑模控制中的抖振,設(shè)計(jì)如下快速連續(xù)終端控制律 τsmc=-(λ1s+λ2sr5/r6) (14) 其中 0 λ1=diag(λ11,λ12,…,λ1n) λ2=diag(λ21,λ22,…,λ2n) 式中λ1i、λ2i(i=1,2,…,n)為正常數(shù)。 注2:文獻(xiàn)[7]的滑模控制器采用了符號(hào)函數(shù),盡管能夠?qū)崿F(xiàn)有限時(shí)間收斂,但是容易引起抖振。而(14)中采用了連續(xù)的非奇異快速終端滑模控制,能夠有效地降低滑模控制的抖震,并提高系統(tǒng)的魯棒性。 RBFNN具有很好的近似未知和平滑函數(shù)的能力[18]。根據(jù)Stone-Weierstrass近似定理,給定足夠數(shù)量的神經(jīng)元,RBFNN能夠以任意精度逼近任意連續(xù)的非線性函數(shù)[19]。 采用RBF神經(jīng)網(wǎng)絡(luò)逼近f∈Rn,f能夠精確表達(dá)(9)中未知非線性函數(shù),即 (15) (16) (17) 其中i=1,2,…,n;j=1,2,…,L; 本文設(shè)計(jì)自適應(yīng)神經(jīng)網(wǎng)絡(luò)逼近機(jī)械臂跟蹤系統(tǒng)中的非線性函數(shù)(9),可以有效減少逼近誤差對(duì)系統(tǒng)的影響。因此根據(jù)(13)(14)和(16),控制輸入(12)可以被重新表示為 (18) (19) (20) 設(shè)計(jì)飽和因子下限φ的倒數(shù)φ-1的自適應(yīng)律為 (21) 定理1:在執(zhí)行器飽和情況下,模型不確定的機(jī)械臂(1)在控制器(18)、自適應(yīng)規(guī)律(19)、(20)、(21)作用下,能夠在有限時(shí)間 (22) 內(nèi)收斂到給定跟蹤軌跡,且跟蹤誤差在原點(diǎn)的極小鄰域內(nèi)。 取Lyapunov函數(shù)為 (23) 定義 (24) (25) V1對(duì)時(shí)間t求導(dǎo)可得 (26) 將式(18)代入式(26)可得 (27) V2對(duì)時(shí)間t求微分可得 (28) 由(27)和式(28)可得 (29) 下面分3種情況討論Hw (30) (31) (32) 同樣地,對(duì)Hε分三種情況分別討論,可得 (33) 同時(shí)可得以下不等式 (34) (35) (36) 將式(30)-(36)代入式(29)得 (37) 根據(jù)文獻(xiàn)[20]可得 (38) 將式(24)、(37)代入式(38)得 (39) 式(39)可寫為 (40) Geomagic Touch機(jī)器人實(shí)物圖如圖1所示,它有三個(gè)旋轉(zhuǎn)驅(qū)動(dòng)關(guān)節(jié)q1、q2、q3,圖2給出Geomagic Touch的平面結(jié)構(gòu)圖。第一關(guān)節(jié)q1為圖中球形底座,q2、q3為與其相連接的桿狀部分,不考慮最后一節(jié)手寫筆狀態(tài),它只是為了人為操縱第三關(guān)節(jié)末端位置。 圖1 Geomagic Touch 圖2 平面結(jié)構(gòu)圖 由于機(jī)械臂第二第三關(guān)節(jié)運(yùn)動(dòng)在同一水平面上,為簡(jiǎn)化運(yùn)算,這里將第二關(guān)節(jié)鎖定,只取第一和第三關(guān)節(jié)的角度變量q1、q3進(jìn)行研究。 Geomagic Touch中各個(gè)矩陣和向量具體表達(dá)式如下 其中 ci=cos(qi);si=sin(qi);c2.i=cos(2qi);s2.i=sin(2qi)。(i=1,3) 設(shè)定機(jī)械臂關(guān)節(jié)的初始位置為 q1=0.1,q3=0.1 設(shè)定機(jī)械臂關(guān)節(jié)的初始速度為 機(jī)械臂所受外部干擾為 τd1=sin(t),τd2=sin(t) 給定所需跟蹤的目標(biāo)軌跡為 qd1=2*sin(t),qd3=2*sin(t) Geomagic Touch機(jī)械臂參數(shù)如表1所示。 表1 Geomagic Touch參數(shù) 仿真中所取控制器的參數(shù)如表2所示。 表2 控制器參數(shù)取值 神經(jīng)網(wǎng)絡(luò)參數(shù)為 由GeomagicTouch性能指標(biāo)可知,其最大輸出力矩為3.3N。當(dāng)超出最大輸出力矩時(shí)機(jī)械臂執(zhí)行器處于飽和狀態(tài)下。 圖3 帶飽和控制器,機(jī)械臂位置跟蹤 圖3和圖4表示機(jī)械臂不帶負(fù)載時(shí),在給定輸出力矩大于最大輸出力矩(3.3N)時(shí),執(zhí)行器處于飽和狀態(tài)下,機(jī)械臂GeomagicTouch在控制器(18)及自適應(yīng)律(19)-(20)作用下,關(guān)節(jié)1和關(guān)節(jié)3的位置和速度跟蹤效果。可以看出機(jī)械臂的位置和速度可以在0.3秒內(nèi)跟蹤到期望軌跡上。圖5和圖6更加直觀地給出了機(jī)械臂跟蹤時(shí)位置和速度的誤差,位置誤差在0.2秒時(shí)小于0.005rad,速度誤差在0.3秒時(shí)小于0.05rad/s。從圖3-圖6可以看出,當(dāng)執(zhí)行器飽和時(shí),模型不確定的機(jī)械臂能夠以很小的誤差跟蹤給定軌跡。 圖4 帶飽和控制器,機(jī)械臂速度跟蹤 圖5 帶飽和控制器,機(jī)械臂位置誤差 圖6 帶飽和控制器,機(jī)械臂速度誤差 為了說(shuō)明本文算法的有效性,與滑模面為線性的算法進(jìn)行了仿真對(duì)比。 表3 控制器參數(shù)取值 圖7 線性滑模面時(shí),機(jī)械臂位置跟蹤 圖8 線性滑模面時(shí),機(jī)械臂速度跟蹤 圖9 線性滑模面時(shí),機(jī)械臂位置誤差 圖10 線性滑模面時(shí),機(jī)械臂速度誤差 具有執(zhí)行器飽和的機(jī)械臂,在控制器為 沒(méi)有飽和因子處理執(zhí)行器飽和時(shí),從圖11-圖12可以看出,機(jī)械臂處于飽和狀態(tài)時(shí),機(jī)械臂無(wú)法實(shí)現(xiàn)位置、速度的穩(wěn)定跟蹤。 圖11 無(wú)飽和控制器,機(jī)械臂位置跟蹤 圖12 無(wú)飽和控制器,機(jī)械臂速度跟蹤 帶負(fù)載時(shí),機(jī)械臂模型為不確定性,機(jī)械臂在控制器(18)及自適應(yīng)律(19)-(20)作用下,用RBFNN神經(jīng)網(wǎng)絡(luò)逼近不確定的矩陣參數(shù),由仿真結(jié)果圖13-圖16可以看,在控制器參數(shù)不改變的情況下,系統(tǒng)依舊可以保持穩(wěn)定。 圖13 帶負(fù)載時(shí),機(jī)械臂位置跟蹤 圖14 帶負(fù)載時(shí),機(jī)械臂速度跟蹤 圖15 帶負(fù)載時(shí),機(jī)械臂位置誤差 圖16 帶負(fù)載時(shí),機(jī)械臂速度誤差 本文研究了執(zhí)行器飽和下,機(jī)械臂的穩(wěn)定性問(wèn)題。首先利用參數(shù)自適應(yīng),辨識(shí)出執(zhí)行器飽和因子下限,有效地解決了執(zhí)行器因?yàn)轱柡投鵁o(wú)法增加力矩,從而無(wú)法達(dá)到預(yù)期跟蹤的問(wèn)題;然后利用權(quán)值自適應(yīng)的徑向基神經(jīng)網(wǎng)絡(luò)辨識(shí)機(jī)械臂的未知參數(shù)以及外部擾動(dòng);最后設(shè)計(jì)非奇異終端快速滑模控制器使得機(jī)械臂系統(tǒng)能夠在有限時(shí)間內(nèi)跟蹤給定軌跡,并有效解決奇異問(wèn)題。在仿真驗(yàn)證算法時(shí),利用Geomagic Touch機(jī)械臂模型,給定輸入力矩大于機(jī)械臂額定力矩,使執(zhí)行器處于飽和狀態(tài),機(jī)械臂可以快速跟蹤給定軌跡,達(dá)到穩(wěn)定效果。在接下來(lái)的工作里,將控制器放在遙操作系統(tǒng)中,考慮時(shí)延和反饋力的問(wèn)題進(jìn)行進(jìn)一步研究。3 控制器設(shè)計(jì)


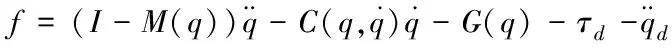

3.1 滑模面設(shè)計(jì)






3.2 RBFNN設(shè)計(jì)







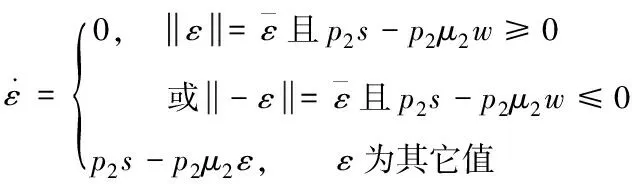

3.3 飽和因子的自適應(yīng)律
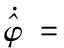



4 穩(wěn)定性分析







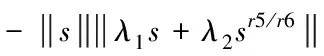


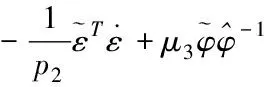
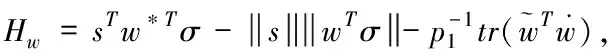




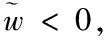


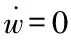
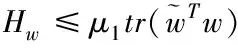










5 仿真





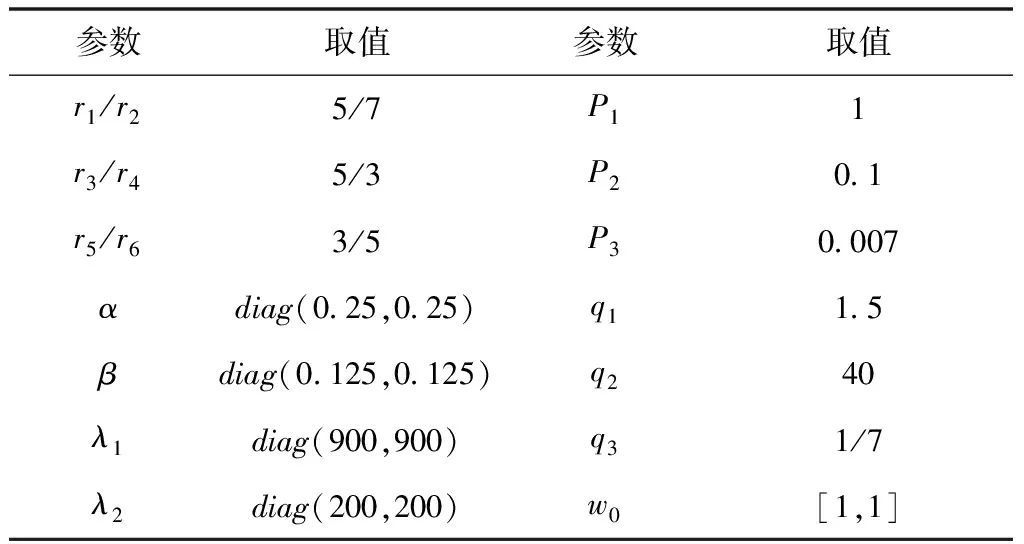

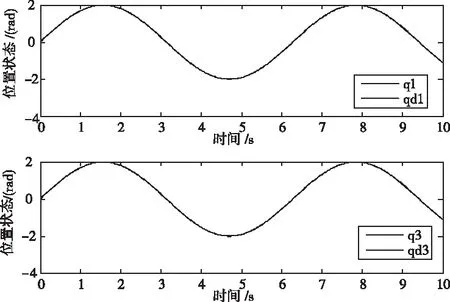
5.1 有執(zhí)行器飽和處理


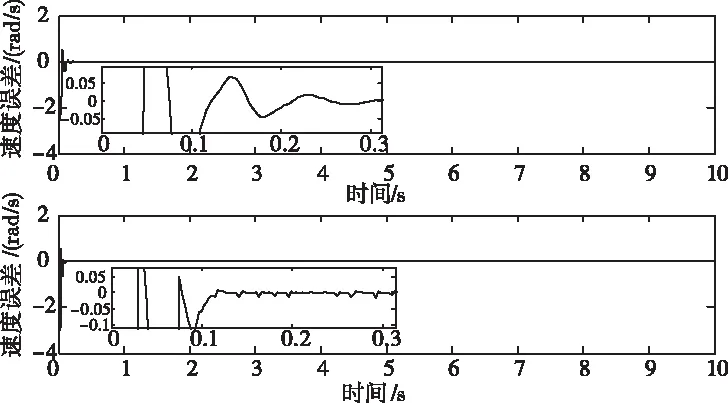


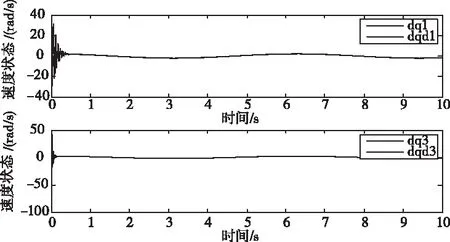

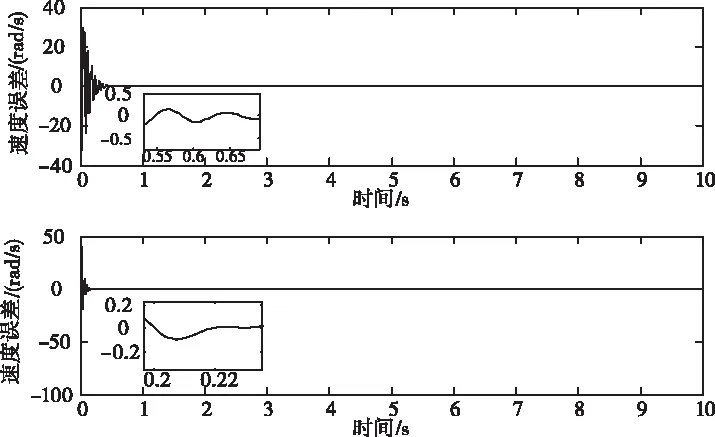
5.2 無(wú)執(zhí)行器飽和處理


5.3 帶負(fù)載仿真
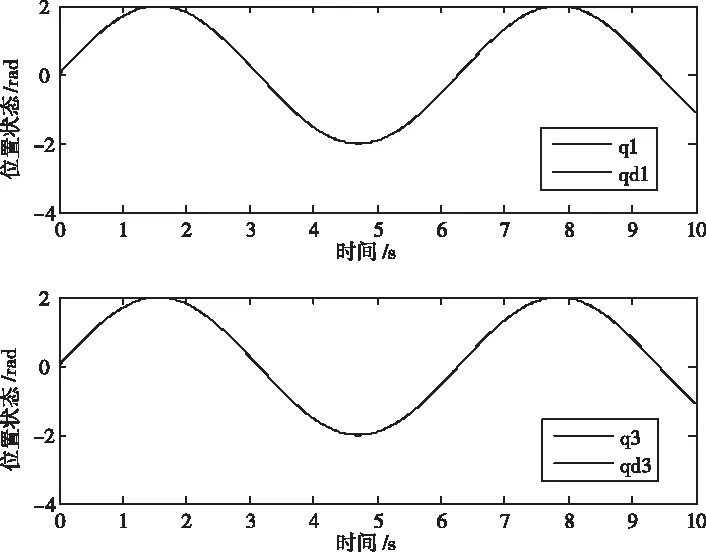



6 結(jié)論

