動態演化SEIRS網絡病毒傳播模型和控制

王俊嶺，羅智榮，郭翠芳，劉 娟

(江西理工大學信息工程學院，江西 贛州 341000)

1 引言

計算機網絡病毒，是指一種能夠通過互聯網進行傳播的惡意程序。隨著計算機網絡的不斷發展，網絡病毒也隨之不斷進化，種類更加復雜、隱蔽性更強、傳播更迅速、制造病毒的手段更加多元化[1]。隨著移動互聯網和物聯網時代的來臨，網絡給人們日常工作、學習和生活帶來極大便利的同時，也給病毒在互聯網中的傳播埋下隱患。病毒的不斷發展不僅給社會造成巨大的經濟損失，甚至于會危及到人類的生命安全。比如目前新興的自動駕駛汽車，遠程操控手術技術等，一旦被網絡病毒感染，后果不堪設想。因此研究網絡病毒的傳播規律，掌握控制網絡病毒的傳播手段具有重大意義。目前，國內外對網絡病毒傳播研究的模型分為微觀模型和宏觀模型，微觀模型指的是研究網絡病毒的代碼本身從而建立反病毒軟件；而宏觀模型，則是借鑒生物傳染病的倉室[2]，結合網絡特征建立網絡病毒傳播的倉室模型，以此來研究各種倉室中病毒在不同傳播條件下的傳播規律，從而找到控制病毒傳播的方法。本文研究網絡病毒傳播的手段，借鑒生物傳染病倉室模型，結合網絡病毒傳播特征，提出了病毒在不同傳播條件下的SEIRS模型，從宏觀角度研究網絡病毒的傳播和控制。

國內外學者對網絡病毒傳播規律進行了深入研究，Cohen等[2]提出可以運用傳染病動力學領域的倉室建模技術來了解網絡病毒的傳播規律；Kephart[5]借鑒一類經典的傳染病SIS倉室模型，成功建立了最早的計算機病毒傳播倉室模型；Ren等[2]建立了一個具有飽和傳染率的 SIR 模型；馮麗萍等建立了一個改進的SIR模型[7]；HAN等人引入時滯來反映病毒傳播的潛伏期，建立了SIRS 模型[7]；Wang 等建立了SIQR病毒時滯擴散模型[9]；劉啟明等建立了一類具有分布時滯的SIRS網絡病毒傳播模型[10]；王剛等建立的潛伏機制下的網絡病毒傳播SEIQRS模型[10]。然而，現有研究模型都存在不足之處。現實中，由于全球時間地域和用戶習慣的不同，任何時刻都可能有新的節點接入和舊的節點下線，網絡節點數量時刻處于動態變化之中；易感節點在受到網絡病毒的攻擊后，由于網絡病毒應用背景和目的不同，潛伏的時間長短也不同，時延長短很難確定，因此以上模型存在較大限制因素。本文充分考慮現實中網絡節點動態變化情況，基于網絡病毒的潛伏性特點以及節點狀態轉移參數改變對病毒傳播和系統穩定性的影響，建立了與此相對應的動態演化SEIRS網絡病毒傳播模型。

2 網絡病毒傳播模型

參照SEIR模型[11]進行改進得圖1 DynSEIRS模型，為了方便后續的模型分析，本文重新定義一些符號如下：

S(t)：在t時刻未感染病毒且沒有免疫力的節點，稱為易感節點，簡寫為S(S≥0)

E(t)：在t時刻感染病毒但病毒處于潛伏期的節點，稱為潛伏節點，簡寫為E(E≥0)。

I(t)：在t時刻感染了病毒且病毒發作的節點，稱為感染節點，簡寫為I(I≥0)。

R(t)：在t時刻對病毒有免疫力的節點，稱為免疫節點，簡寫為R(R≥0)。

最初，網絡中的所有結點都是正常運行的，且只存在易感節點和感染節點，一旦受到網絡病毒的襲擊，各節點狀態將會遵循以下規則的轉換：(A1)由于全球時間地域和用戶習慣的不同，不同的節點聯入網絡的時間也是不同的，因此不斷有新節點以δ>0的恒定速率聯入，且聯入的新節點都是易感的。同理，有不斷的節點以恒定速率δ>0斷開下線。

(A2)對于易感狀態節點S，由于病毒的入侵，每個易感節點因與感染節點通信而轉換成潛伏節點，設每次信息發送接收，傳染病毒的概率為β0，單位時間內一個易感節點與其它節點進行信息共享的次數U，則平均有效傳染率為β0U，根據以上定義，t時刻所有已感染病毒的節點感染的新節點數為β0USI/N，其中N為網絡節點總數。根據 Guan等[12]研究得知，接觸次數U與節點度k成正比，即U=β1k，記β=β1β2為潛伏節點的感染系數，從而單位時間內被病毒感染的新節點數為βkSI/N。

(A3)對于易感狀態節點S，每個易感節點因安裝最新版本的殺毒軟件而轉化為免疫節點的單位時間概率為ω，ω>0。

(A4)對于潛伏節點E，每個潛伏的病毒被激活，而轉化為感染節點的單位時間概率為γ，γ>0，因系統重裝而轉化為易感節點的單位時間概率為θ，θ>0，又因用殺毒軟件及時查殺病毒而轉化為免疫節點的單位時間概率為ε，ε>0。

(A5)對于感染節點I，每個感染節點在病毒攻擊網絡時被用戶查殺而轉化為免疫節點的單位時間概率為μ，μ>0。

(A6)對于免疫節點R，每個免疫節點因殺毒軟件過期或因重裝系統而轉化為易感節點的單位時間概率為α，α>0。

圖1 DynSEIRS模型的狀態轉移圖

根據系統動力學原理及假設模型的狀態轉移圖，可得DynSEIRS模型數學表達式如下

(1)

3 穩定性分析

由于R=N-S-E-I，式( 1) 可進一步簡化成如下平面系統

(2)

其初始條件為：S(0)≥0，E(0)≥0，I(0)≥0，正向不變集為

Ω={(S，E，I)|S≥0，E≥0，I≥0，S+E+I≤N}

本小節通過求方程組( 2) 的平衡點并且研究系統在平衡點的穩定性來分析模型反映的病毒傳播機理。令

(3)

借鑒文獻[13]基本再生數的概念。根據式(2)中參數的物理意義，可得

(4)

S*=(δ+γ+ε+θ)(μ+δ)N/βγk

(5)

E*=(μ+δ)I*/γ

(6)

(7)

根據式(2)式可得任意平衡點P* 的 Jacobi 矩陣

J(P*)>

(8)

定理1：當R0≤1時，式(2)在D內僅有唯一的無毒平衡點P0局部漸近穩定。

證明：由式(8)可得平衡點P0處Jacobi 矩陣

J(P0)>

(9)

矩陣J(P0) 的特征多項式為

(λ+δ+ω+α)(λ+θ+δ+ε+γ)(λ+μ+δ)=0

(10)

其對應特征根λ1=-μ-δ，λ2=-ω-δ-α，λ3=-θ-δ-ε-γ顯然，當R0≤1時，λ1，λ2和λ3根的實部均為負，無毒平衡點P0局部漸近穩定。

定理1表明，當R0≤1時，網絡中最終只存在易感節點和免疫節點，感染節點和潛伏節點都隨時間趨于0，網絡病毒全部被消滅。

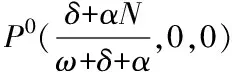
證明：由式(8)可得平衡點P1處Jacobi 矩陣

(11)

其對應的特征多項式為：λ3+b1λ2+b2λ+b3=0。其中：

當R0>1時，b1>0，b2>0，b3>0。根據Hurwitz定理，計算可得

由Hurwitz判據可得特征方程的根的實部均為負，即J(P1)的特征值實部全部為負。因此可得結論： 當R0>1 時，平衡點P1=(S*，E*，I*)是局部漸近穩定。

定理2表明，當R0>1 時，網絡中潛伏節點和感染節點將以一定的比值持續穩定存在，網絡病毒最終不能完全被消滅。根據定理1和定理2可知，可以調節參數使R0≤1，來控制和消除網絡病毒的傳播。

4 數值模擬與分析

為了觀察微分方程(2)刻畫的網絡病毒的傳播過程，研究各參數變量動態演化規律，本小節圍繞系統基本再生數R0=βkγ(α+δ)/(δ+θ+γ+ε)(δ+μ)(ω+δ+α)，重點分析S-E狀態傳染率β、S-R狀態轉移概率ω和R-S狀態轉移概率α三個參數及新舊節點的上下線率δ對病毒傳播的影響，進而驗證模型的有效性及系統隨時間的演進關系。仿真的目的主要是：①驗證定理1，2理論分析的正確性；②在系統其它參數不變的情況下，改變狀態轉換參數來觀察模型的網絡病毒傳播過程；③分析狀態轉換參數對網絡病毒的傳播影響，得出有利于控制網絡病毒傳播的結論。

圖2 SEI相圖

圖3 SIR相圖

分別設置系統變量的初值和相關參數，設置網絡節點總數N=1，網絡節點平均度k=30，最初，網絡節點都是正常運行的，且只存在易感節點和感染節點，開始S和I為隨機數量，其它參數的基本設置為：δ=0.0001，μ=0.08，θ=0.06，β=0.02，γ=0.2，ω=0.3，ε=0.06，α=0.02。計算得R0=0.293。由MATLAB仿真得到圖2和圖3。

由圖2和圖3相圖可知，在R0=0.293<1情況下，無論易感節點S和感染節點I的初始值怎樣分布，結果潛伏節點E和易感節點I都隨著時間逐漸趨于0，病毒最終被完全消滅。而易感節點S和免疫節點R最終隨時間趨于穩定，系統局部漸近穩定在無病毒平衡點P0處。這表明易感節點S和感染節點I的初始值，不會影響無病毒平衡點P0的位置。

4.1 S-R狀態轉移概率ω對病毒的傳播影響

為了研究參數ω對網絡病毒的傳播影響，本文運用控制變量的方法，保持其它參數值不變，調整ω的值并分析其對病毒傳播的影響。根據基本再生數R0，計算得S-R狀態轉移概率ω的閾值為ωlim=0.074。當ω>ωlim時R0<1，系統局部漸近穩定在無病毒平衡點P0；當ω<ωlim時R0>1，系統局部漸近穩定在有毒平衡點P1處。當ω=0.2時，R0=0.427<1，仿真結果如圖7所示，從圖4中可明顯看出，感染節點隨時間趨于0，病毒最終被完全消滅。當ω=0.04時，R0=1.565>1。仿真結果如圖5所示，從圖5中可明顯看出，感染節點隨時間趨于穩定，但網絡病毒最終無法完全被消滅。

圖4 ω=0.2時DynSEIRS隨時間的數量變化

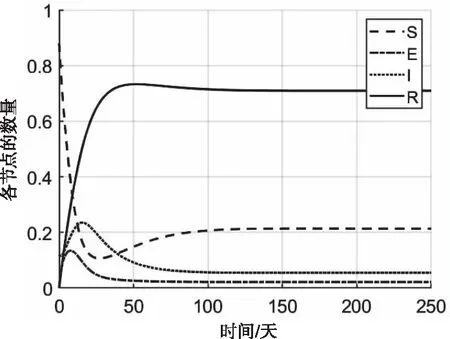
圖5 ω=0.04時DynSEIRS隨時間的數量變化

圖6 在不同ω值下感染節點數隨時間變化

圖6是ω在不同值下，感染節點數隨時間的變化曲線仿真圖，其中，ω在區間[0.01，0.16]中取值，步長為0.5。當ω=0.01，0.06<ωlim時，系統局部漸近穩定在有毒平衡點P1處，感染節點無法完全被消滅；當ω=0.11，0.16>ωlim時，系統局部漸近穩定在無病毒P0處。病毒全部被消滅，仿真結果與理論分析一致。隨著ω值不斷增大，感染節點逐漸減少，這表明安裝和更新最新的殺毒軟件能有效的控制病毒的傳播。當ω超過閾值ωlim即R0≤1時，病毒可以完全被消滅。所以，可以通過適當調控ω來有效控制和消除病毒的傳播。

4.2 R-S狀態轉移概率α對病毒的傳播影響

為研究參數α對網絡病毒的傳播影響，根據基本再生數R0，計算得R-S狀態轉移概率α的閾值為αlim=0.0814。當α<αlim時R0<1，系統局部漸近穩定在無毒平衡點P0處；當α>αlim時R0>1，系統局部漸近穩定在有毒平衡點P1處。當α=0.04時，R0=0.552<1，仿真結果如圖7所示，從圖7中可明顯看出，感染節點隨時間趨于0，網絡病毒最終被完全消滅。當α=0.2時，R0=1.873>1。仿真結果如圖8所示，從圖8中可明顯看出，感染節點隨時間趨于穩定，但是網絡病毒最終無法被完全消滅。

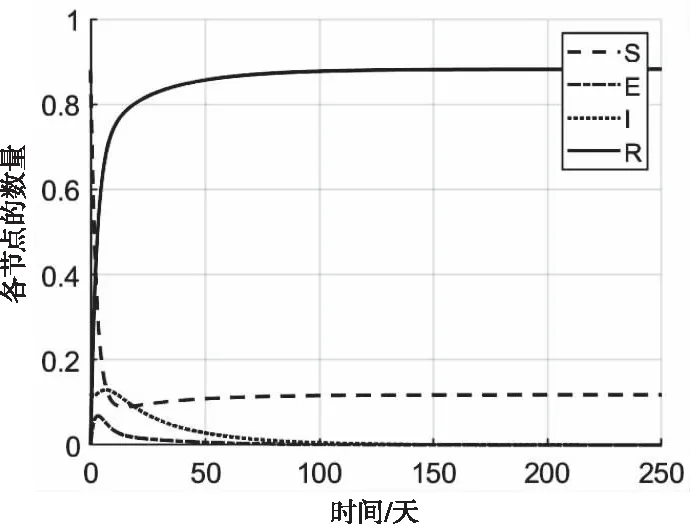
圖7 α=0.04時DynSEIRS隨時間的數量變化

圖8 α=0.2時DynSEIRS隨時間的數量變化

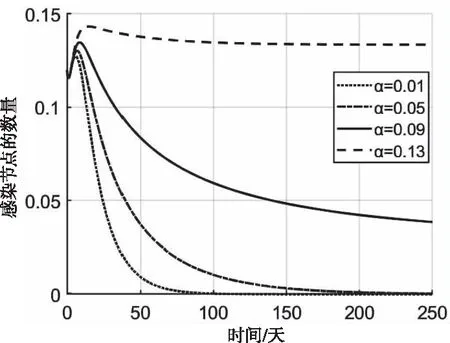
圖9 在不同α值下感染節點數隨時間的變化

圖9表示的是，在α的不同值下，感染節點數隨時間的變化曲線。其中，α在區間[0.01，0.13]中取值，步長為0.4，當α=0.01，0.05<αlim時，系統局部漸近穩定在無毒平衡點P0處；當α=0.09，0.13>αlim時，系統局部漸近穩定在有毒平衡點P1處，感染節點無法被完全消滅，仿真結果與理論分析一致。隨著α值不斷增大，感染節點逐漸變大，這證明節點在無殺毒軟件或殺毒軟件失效時，易感節點更容易被病毒傳染。當α小于閾值αlim即R0≤1時，網絡病毒可以完全被消滅。所以，可以通過適當調控α來有效控制病毒的傳播。

4.3 新舊節點上下線率δ對病毒的傳播影響

在全球中，由于時間地域的跨度不同，隨時都有新節點的加入和舊節點的下線，整個系統都是動態演變的。為分析新舊節點上下線率δ對網絡病毒傳播的影響，通過調整新舊節點上下線率δ的大小，分別仿真當δ=0.01，0.1，0.2，0.3，0.5時，感染節點數隨時間的變化曲線，仿真結果如圖10所示。通過對比這五條曲線，可以明顯的看出，隨著δ的增大，感染節點趨于零的時間越來短。這表明：用戶集中上下線有助于控制網絡病毒的傳播。所以，有效抑制病毒的傳播可以通過合理的調控δ。

圖10 在不同δ值下感染節點數隨時間的變化

研究結果表明，S-R狀態轉移概率ω和R-S狀態轉移概率α影響著病毒在計算機網絡中是長久存在還是趨于滅絕，新舊節點上下線率δ影響著網絡病毒的治愈時長。通過增大轉移概率ω和減小轉移概率α，增大新舊節點上下線率δ可有效迅速的控制和消除網絡病毒的傳播。

5 結語

本文建立了動態演化SEIRS網絡病毒模型DynSEIRS，該模型充分考慮了網絡中各節點數量的動態變化及在計算機病毒的潛伏性特點下狀態轉移參數對病毒傳播的影響，彌補了現有模型因忽略網絡中節點上下線動態演化所帶來的不足，使模型能更客觀地反映現實中計算機網絡病毒傳播情況。系統的分析了模型的動力學行為，研究表明，S-R狀態轉移概率ω，R-S狀態轉移概率α和新舊節點的上下線率δ對網絡病毒的傳播有著很大影響，當α小于而ω大于各自對應的閾值時，系統穩定在無毒平衡點上，網絡病毒最終完全被消滅，一旦α超過而ω小于各自對應的閾值時，系統將穩定在有毒平衡點，病毒最終不能被完全消滅；網絡病毒被治愈的時間也隨著δ的增大而變得越來越小。因此，在網絡安全防御行動中，為了有效控制并消除病毒在網絡中的傳播，最有效且可行的辦法就是通過增大轉移概率 ω、減小轉移概率α 和增大新舊節點上下線率δ。