Lv混沌系統的反饋控制仿真研究

王偉豪，劉樹勇，諶 龍

(海軍工程大學動力工程學院，湖北武漢 430033)

1 引言

混沌現象是一種看似無規則但是具有內在隨機性的復雜現象，廣泛存在于氣象，物理，經濟，通信等各個領域[1]。目前，國內外學者對混沌系統的控制提出了許多不同的方法，大致可分為反饋控制法和非反饋控制法[2]。1990年，Lima等[3]提出了基于參數共振微擾的非反饋控制方法，其應用于Duffing系統中達到混沌抑制。此后學者們對混沌系統的控制與應用進行了廣泛的研究，并取得了一系列的研究成果[4-11]。由于混沌系統的反饋控制具有較為完善的理論分析，衍生出了一系列反饋控制的方法，如追蹤控制[4，5]、自適應控制[6，7]、分岔控制[8，9]、微分控制[10，11]等。這些控制策略控制可以使系統穩定于平衡點或周期軌道，但在某些應用場合也存在一些不足。首先，反饋控制的實現前提必須對系統的狀態變量進行物理測量，這在實際工程中較難實現。其次，混沌系統對初始條件極為敏感，測量過程中會不可避免的受到外界噪聲的干擾，從而影響系統的精確控制。

利用非共振參數策動實現混沌控制[12]是近幾年提出的一種針對自治混沌系統的非反饋混沌控制方法，該方法不僅避免了對混沌狀態變量的測量，而且可以通過嚴格的理論分析求解控制參數，有利于推廣應用。諶龍等[13]利用自治混沌系統的參數非共振激勵混沌抑制原理實現Lorenz系統由混沌狀態到大周期狀態的轉變，該控制方法可用于檢測相同頻率的方波信號。王夢蛟等[14]利用非共振參數策動在一定信噪比范圍內實現對Chen系統的非反饋混沌控制。Lv系統作為連接Lorenz系統與Chen系統的橋梁的典型自治混沌系統，其豐富的動力學行為得到了廣泛的研究[15，16]，在工程中具有可觀的應用前景。而混沌控制是混沌應用的關鍵，因此如何實現對Lv系統的有效控制具有重要的意義。

本文首先對Lv系統進行線性狀態反饋反饋控制，分析了Lv系統的平衡點穩定性，利用霍爾維茨判據確定負反饋控制參數，仿真表明所得參數可將呂系統控制到指定的平衡態和振蕩周期軌道上。然后通過施加非共振激勵實現非反饋混沌控制，采用平均法和Lyapunov方法得到控制參數應滿足的條件，仿真研究表明此方法可將系統狀態變量達到很好的控制，且具有較強的抗干擾性能。

2 呂系統及穩定性分析

2002年，呂金虎等人通過混沌反饋控制得到混沌呂系統，作為連接Chen系統和Lorenz系統的橋梁，它很快就引起了人們的關注，吸引子由如下三維系統產生

(1)

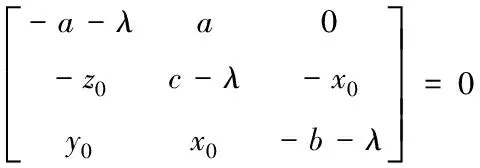
(2)

根據式(2) 可求得各平衡點所對應特征根有正實部，因此這些平衡點都是不穩定的，從相圖1可以看出，它有著豐富的動力學行為。

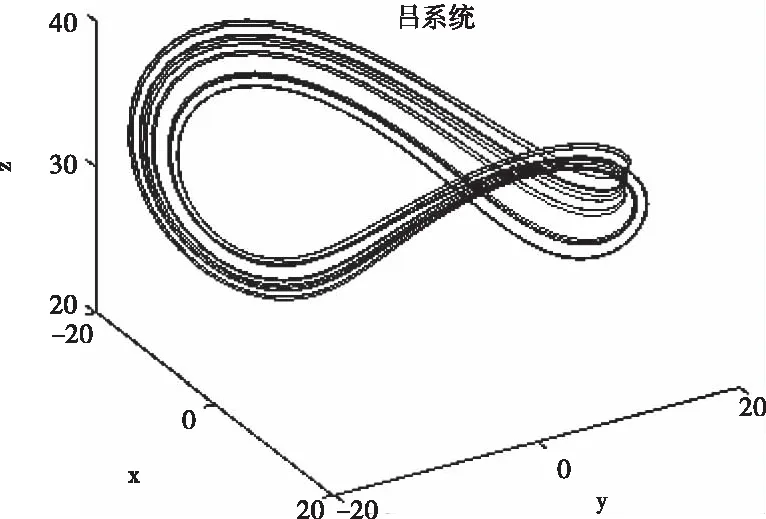
圖1 呂混沌吸引子

3 呂系統的負反饋控制

3.1 控制參數的確定

在呂系統的第二式中加入負反饋-kx，得到

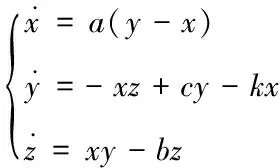
(3)

(4)

則特征根均具有負實部，平衡點是漸近穩定的。如果滿足條件

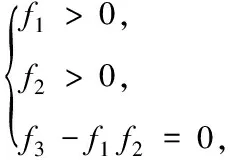
(5)

則特征值有一負的實根和一對零實部的共軛復根，系統出現穩定的極限環，振蕩周期為2π(b2)-1/2。通過(4)、(5)式穩定條件，分別針對三個平衡點P1，P2，P3的負反饋控制條件進行求解，理論結果見表1．

表1 負反饋控制理論值

3.2 仿真研究結果

系統初值取為(0.5，0.8，1)，當k=30，特征根λ=-3.5±7.5993i和-3，均為負實部，零解漸進穩定，系統(3)最終被吸引到原點P1上，數值研究結果如圖2所示，由圖2(b)看出系統經過短暫時間后趨于原點P1(0，0，0)。

圖2 混沌狀態的控制k=30

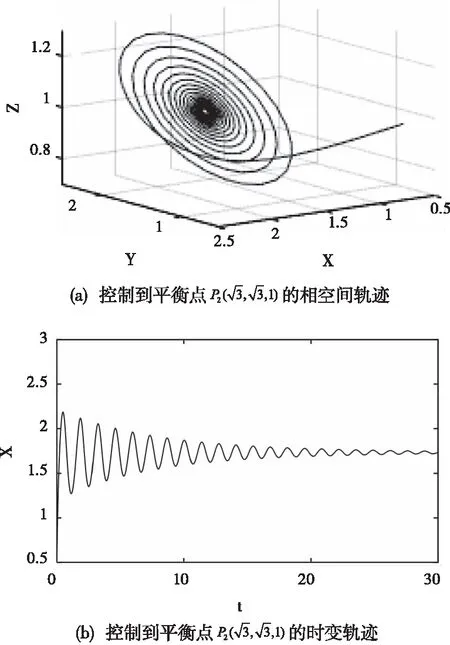
圖3 混沌狀態的控制k=27

圖4 系統控制到極限環上k=161/6

4 呂系統的非反饋控制

4.1 控制系統描述

在實際應用中，控制信號的輸入往往會受到環境噪聲的干擾，從而影響控制效果。為分析呂控制系統的抗干擾能力，當激勵參數k=21時，將方差為5的高斯白噪聲加入到激勵信號中，得到信噪比為9.8dB的控制輸入μ(t)，其波形如圖所示。在激勵控制信號中加入噪聲的情況下，系統依然能夠迅速得到控制，其中狀態變量z(t)隨時間的變化如圖8所示，與圖6(b)中無噪聲的激勵控制相比，兩種情形下控制的時間基本相同，區別在于未加噪聲時的控制效果為97.19%，輸入含噪聲時的控制效果達到96.35%，說明控制系統的抗干擾性能較好。

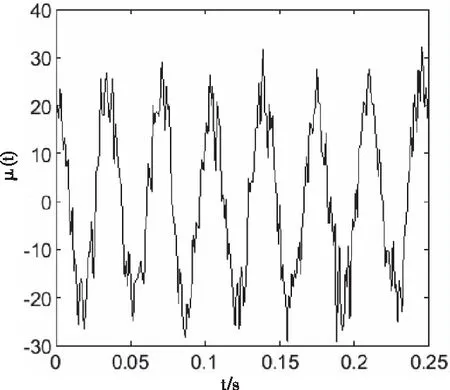
圖7 噪聲干擾下控制輸入μ(t)的波形

圖8 輸入含噪聲時狀態變量z的控制效果

5 結論

本文對呂系統的混沌行為進行了研究分析，采用負反饋和非反饋控制的方法有效地控制Lv系統混沌并得出一下結論：

1)負反饋控制不需改變系統的參數和結構就可以使系統趨于指定的平衡態或振蕩周期上，數值仿真與理論分析得到了一致的結果；

2)對Lv混沌方程組的第二項施加頻率遠大于系統特征頻率的周期信號，用平均法對控制系統進行處理得到了慢變系統，根據Lyapunov穩定性定理得到控制參數應滿足的條件，通過選取適當參數對混沌系統進行控制，控制效果可達97.8%，且具有較強的抗干擾性能，相比于參數共振微擾方法，此方法可給出嚴格的理論分析，對于微弱信號檢測具有潛在的應用價值。