基于遺傳螢火蟲算法的液壓挖掘機鏟斗控制研究

李 捷，王毫旗

(太原科技大學機械工程學院，山西太原 030024)

1 引言

對挖掘機工作裝置精確的位置控制是實現挖掘機智能化的基礎。本文以某型號小型液壓挖掘機為研究對象，通過對液壓挖掘機鏟斗電液伺服控制系統的研究來實現對鏟斗位置的精確控制。文獻[1]提出了一種改進的粒子群優(yōu)化算法，改善了液壓挖掘機電液伺服系統的響應特性和鏟斗軌跡控制的效果；文獻[2]提出一種慣性權重余弦調整的粒子群優(yōu)化算法用于PID控制參數整定中，使得控制系統響應性能更好；文獻[3]提出構建了死區(qū)模糊補償控制系統，通過將傳統數字PID控制和變死區(qū)補償模糊控制方法的結合，提高了電液比例系統位置控制的精度。文獻[4]提出了一種適應性強的程序，該程序用于提取電液伺服系統的線性化模型，以完成精確的位置控制任務；文獻[5]提出了基于兩相平衡多目標的智能水滴算法(IWD)和多目標優(yōu)化方法，提高了對電液伺服系統的控制性能；文獻[6]提出了一種基于奇異攝動理論的電液負載轉矩跟蹤控制方法，運用期望模型補償的自抗擾控制方法提高系統的高精度和強魯棒性。文獻[7]提出了改進人群搜索算法的優(yōu)化方法，加快了算法的搜索速度，改善了系統的性能；文獻[8]將天牛須搜索算法用于PID控制器的設計，此算法使運算量大大降低，有效縮短了整定時間；文獻[9]提出擬混沌人群搜索算法，改善了局部求精能力和全局搜索能力。

為了實現對液壓挖掘機鏟斗位置的精確控制，在標準遺傳算法的基礎上對目標函數、選擇算子、交叉算子等進行了改進，主要是運用了能夠隨進化過程自適應改變的非線性交叉概率和變異概率，然后再引入人工螢火蟲算法來避免標準遺傳算法的早熟現象，最后提出了歐式距離算法停止準則，有效縮短了算法的運算時間。遺傳螢火蟲算法能夠有效避免陷入局部最優(yōu)的問題，提高了算法的尋優(yōu)精度并且縮短了算法的收斂時間。通過仿真對比，驗證了遺傳螢火蟲算法的優(yōu)越性和有效性。

2 液壓挖掘機鏟斗系統建模

2.1 鏟斗電液比例系統原理組成

液壓挖掘機鏟斗電液比例位置控制系統的結構原理圖，其中包括指令元件、控制器、D/A轉換器、比例放大器、電液比例閥、液壓缸、工作裝置、位移傳感器等元件，結構原理圖如圖1所示。

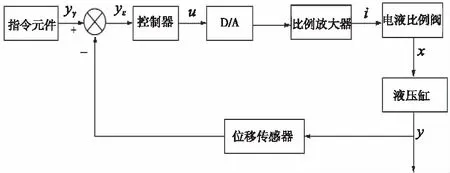
圖1 鏟斗電液比例位置控制系統結構圖

2.2 電液比例閥的傳遞函數

在實際工作中由于電液比例閥的響應速度比工作裝置液壓缸的要快，因此把電液比例閥的一階慣性形式作為傳遞函數，如下方法

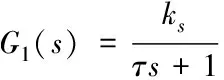
(1)

其中，ks為電液比例閥的流量增益；τ為電液比例閥時間常數。

2.3 電液比例閥控非對稱缸傳遞函數

液壓挖掘機工作裝置油缸系統結構是非對稱液壓缸系統，其液壓缸的傳遞函數由電液比例閥滑閥流量線性化方程、液壓缸流量連續(xù)性方程以及液壓缸力平衡方程經過拉普拉斯變換得到[10]，則液壓缸活塞桿正向伸出時的傳遞函數如下方法

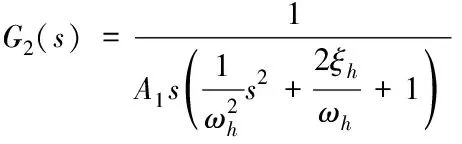
(2)

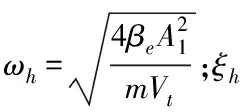
2.4 鏟斗電液比例控制系統傳遞函數

由圖1以及式(1)和式(2)可得鏟斗電液比例控制系統的傳遞函數如下方法

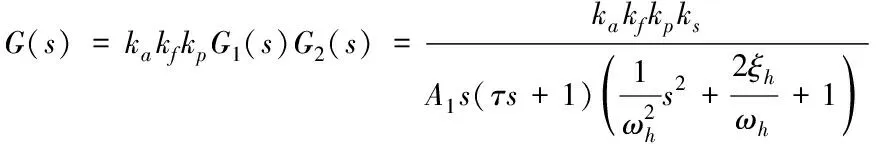
(3)

其中，ka為比例放大器增益；kf為位移傳感器增益；kp為PID控制器比例系數。

電液比例控制系統的主要參數如圖2所示。

符號值符號值Ka0.5A/VVt2.826×10-3m3Kf10V/mβe800MPaKs2.778×10-4m3/s·Akce5.508×10-12A15.675×10-3m2ωh337.6rad/sτ0.05ξh0.01

代入圖2中的參數可得鏟斗電液比例控制系統的傳遞函數如下方法

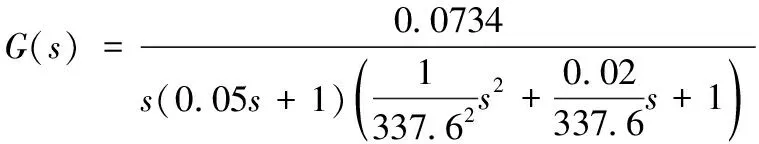
(4)

3 遺傳螢火蟲算法

3.1 改進的遺傳算法

3.1.1 基因編碼及構造初始種群

對參數kp、ki、kd采用二進制編碼形式進行編碼。用長度為10的二進制碼表示，編碼后生成的染色體如下方法

[kp1，…，kp10，ki1…ki10，kd1，…，kd10]

(5)

根據工程方法確定每個參數的取值范圍，然后在范圍之內生成初始種群如下方法

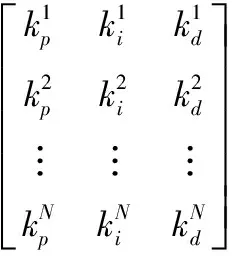
(6)

3.1.2 適應度函數的改進

在ITAE的基礎上對系統評價指標進行改進，將改進后的評價指標作為系統的適應度目標函數，目標函數如下方法

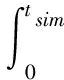
+αOs+βSSe+γts+δtr

(7)

其中，tsim為系統仿真時間；w1，w2為權重；e(t)為系統誤差；u(t)為控制器輸出；α，β，γ，δ為系統性能參數權重；Os為超調量；SSe為穩(wěn)態(tài)誤差，ts為調節(jié)時間，tr為上升時間。適應度函數取目標函數的倒數如下方法

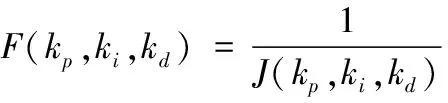
(8)

3.1.3 選擇算子的改進

先按式(7)(8)計算每個個體的適應度值，接著將個體按照其適應度值的大小降序排列，并且將排序之后的個體平均分成五份。將適應度值較高的前五分之一個體按照精英保留策略復制至下一代作為父代親本；然后將適應度值較差的后五分之一個體直接淘汰；最后將中間剩余的五分之三個體按照式(9)—(11)進行選擇。

Pi=Q(1-q)i-1

(9)

(10)

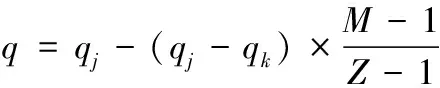
(11)

其中，Pi為第i個個體被選擇的概率；Q為個體的選擇概率；i為中間3/5種群中個體的排列序號；q為最佳個體的選擇概率。因為最佳個體的選擇概率會隨著迭代次數的變化而發(fā)生改變，故提出q值的計算公式如下方法

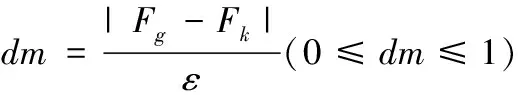
(12)

其中，qj為M代最佳個體選擇概率；qk為M代最差個體選擇概率；Z為最大迭代次數。

3.1.4 交叉算子的改進

遺傳算法中適合二進制編碼的交叉操作有多種形式：單點交叉、兩點交叉、多點交叉以及均勻交叉等。基于算法的可操作性考慮，這里主要運用單點交叉和兩點交叉兩種形式。引入個體的相似度dm，表示種群中兩個體的相似程度。則個體g和k的相似度公式如下方法：

其中，ε為種群中個體適應度最大值與最小值之差，0<ε；Fg為種群中個體g的適應度值；Fh為種群中個體h的適應度值。若0.5≤dm≤1，說明兩個體之間相似程度較低，則使用單點交叉操作；若0≤dm<0.5，說明兩個體相似程度較高，則使用兩點交叉操作。

3.1.5 變異算子

運用均勻變異算子進行單點變異操作，變異時，在染色體上隨機選擇一個二進制碼位進行變異，然后形成新的染色體個體。

3.1.6 交叉概率和變異概率的改進

提出一種新的自適應調整交叉概率和變異概率，自適應調整交叉概率和變異概率的公式如下方法：

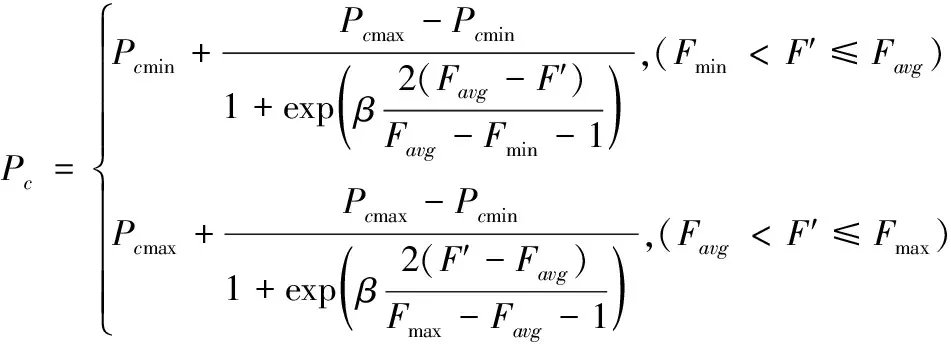
(13)

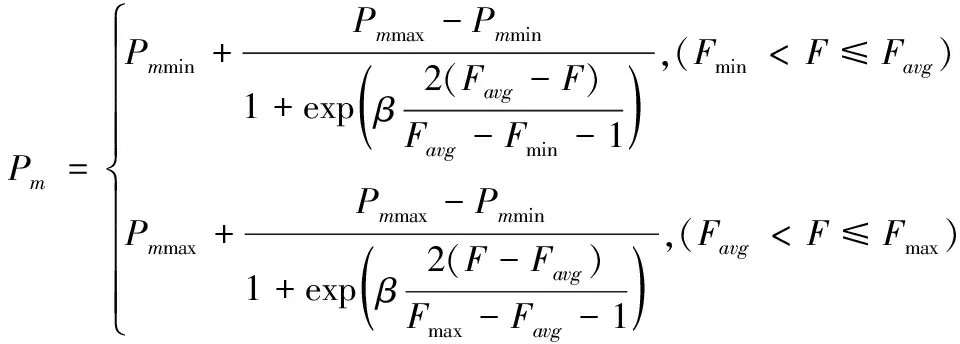
(14)

其中，Pcmax、Pcmin為交叉率的最大值與最小值；β為曲線平滑因子，β=9.9034；Favg為當前種群個體適應度的平均值；Fmax、Fmin為當前種群個體適應度的最大值與最小值；F′為交叉兩個體的較大的適應度值；Pmmax、Pmmin為變異率的最大值與最小值；F為當前個體適應度值。

3.2 人工螢火蟲優(yōu)化算法

螢火蟲算法顧名思義就是通過觀察螢火蟲群體的行為和群體間的交流而提出的一種群智能算法，由劍橋大學的Xin-She Yang教授提出。K.N.Krishnanad和D.Ghose提出了人工螢火蟲群優(yōu)化算法，該算法是一種新型的群智能優(yōu)化算法[11-13]。提出將遺傳算法選擇操作中直接保留的精英個體和經過交叉、變異的個體共同組成較優(yōu)種群Ⅰ，將人工螢火蟲群優(yōu)化算法作用于較優(yōu)種群Ⅰ，能夠提高算法的尋優(yōu)精度和收斂速度，避免陷入局部最優(yōu)。具體操作如下：

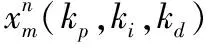
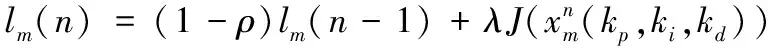
(15)

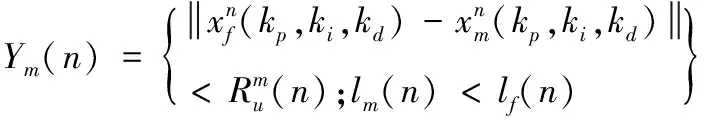
(16)

3)按照式(17)計算螢火蟲m向熒光素值比自己高的螢火蟲f移動的概率pmf(n)，并按式(18)更新螢火蟲m移動后的位置如下方法

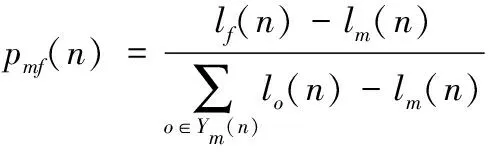
(17)

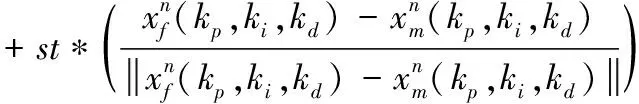
(18)

4)根據式(19)更新動態(tài)決策域的半徑如下方法

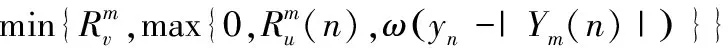
(19)

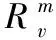
3.3 確定算法停止準則

提出一種停止準則，即歐式距離停止準則。歐式距離停止準則是以每代最優(yōu)的PID參數構成的三維決定向量V[kpkikd]T為依據，計算第k代的決定向量Vk與第k+1代的決定向量Vk+1之間的歐式距離。通過計算連續(xù)多代相鄰決定向量之間的歐氏距離是否小于某一設定值，若小于該設定值則說明達到終止條件，即終止程序。本文采用歐式距離停止準則與最大進化次數共同作為遺傳螢火蟲算法的停止準則，即雙重停止準則，可以有效減少算法的運算時間。

4 遺傳螢火蟲算法的PID參數整定

4.1 經典PID控制器

經典的PID控制器，控制原理比較簡單，適應性較強，是一種典型的線性控制器。其控制規(guī)律滿足如下方法

(20)

其中，e(t)為偏差信號；u(t)為控制器輸出值；kp為比例系數；ki為積分系數；kd為微分系數。通過遺傳螢火蟲算法對PID控制器的參數進行優(yōu)化，其控制框圖如圖3所示。

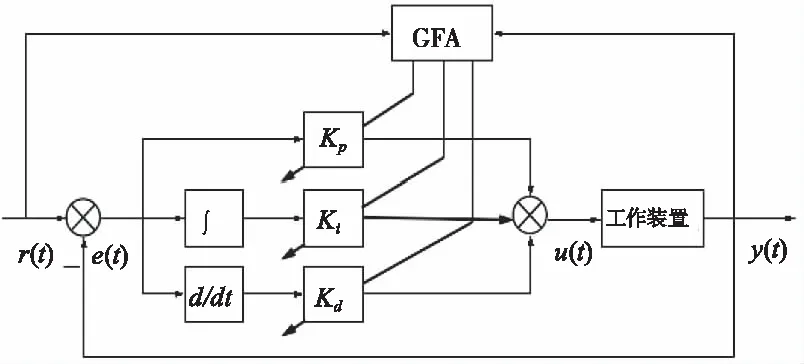
圖3 遺傳螢火蟲算法優(yōu)化PID參數示意圖

4.2 遺傳螢火蟲算法整定PID參數的具體實現步驟

其步驟可總結如下：

1)根據工程方法確定PID控制器各參數的范圍，kp∈[0，100]，ki∈[0，1]，kd∈[0，1]，采用二進制編碼方法對PID控制器的三個參數進行編碼，種群規(guī)模N設為30，然后隨機產生初始種群；

3)計算是否滿足停止準則，若滿足停止條件(達到最大迭代次數100或歐式距離小于設定值)則輸出最優(yōu)解，終止程序，若不滿足停止條件則進行下一步操作；

4)按照式(9)—(11)改進的選擇算子對個體進行復制選擇，然后結合改進的交叉算子以及自適應非線性調整概率公式進行交叉和變異操作，然后產生較優(yōu)種群Ⅰ；

5)引入人工螢火蟲算法對較優(yōu)種群Ⅰ再進行遺傳進化，然后生成較優(yōu)種群Ⅱ，最后合并種群Ⅰ和種群Ⅱ為新的種群進入下一次迭代過程，并返回步驟2)計算個體的適應度值，再根據步驟3)計算是否滿足停止準則，若滿足此準則，終止程序，否則繼續(xù)按照上述步驟進行操作。遺傳螢火蟲算法整定PID參數流程圖如圖4所示。

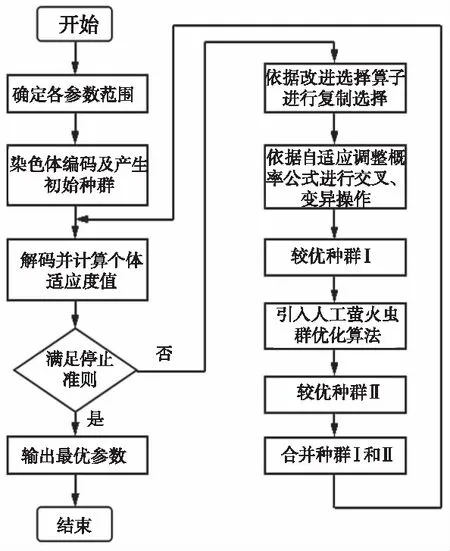
圖4 遺傳螢火蟲算法流程圖

5 仿真設計與結果分析

5.1 確定實驗參數

將標準遺傳算法和遺傳螢火蟲算法的種群規(guī)模均設為30，最大進化次數均設為100。標準遺傳算的交叉概率與變異概率均為固定值，設為Pc=0.8，Pm=0.01。遺傳螢火蟲算法中設Pcmax=0.8，Pcmin=0.3；Pmmax=0.075，Pmmin=0.01。式(10)中取w1=0.999、w2=0.001、α=1.5、β=15、γ=7、δ=1。人工螢火蟲算法中ρ=0.4；λ=0.6；st=0.03；ω=0.08；yn=6。

5.2 仿真設計

運用MATLAB/Simulink模塊來進行仿真設計將標準PID控制與運用標準遺傳算法和遺傳螢火蟲算法的控制進行對比實驗。進一步，在Matlab/Robotic Toolbox中完成挖掘機器人挖掘基坑的軌跡規(guī)劃，為了達到良好的控制效果，采用挖掘機器人關節(jié)空間分段多項式插值法來進行挖掘基坑的軌跡規(guī)劃，將挖掘的過程分為5段軌跡。將規(guī)劃后的數據結果即鏟斗關節(jié)角度值作為期望目標值輸入到控制器中，觀察在各種算法整定下對期望目標值的跟蹤效果。進一步驗證各種算法的整定效果。

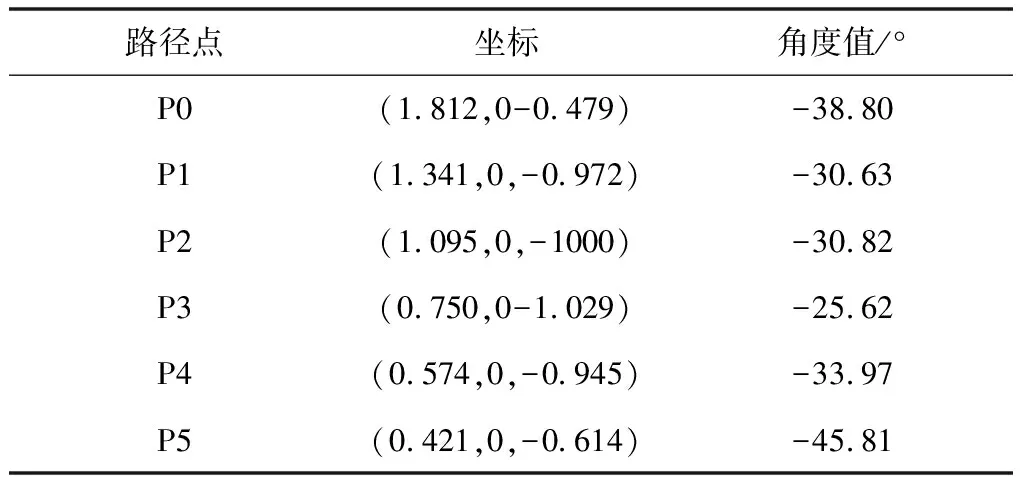
路徑點坐標角度值/°P0(1.812,0-0.479)-38.80P1(1.341,0,-0.972)-30.63P2(1.095,0,-1000)-30.82P3(0.750,0-1.029)-25.62P4(0.574,0,-0.945)-33.97P5(0.421,0,-0.614)-45.81

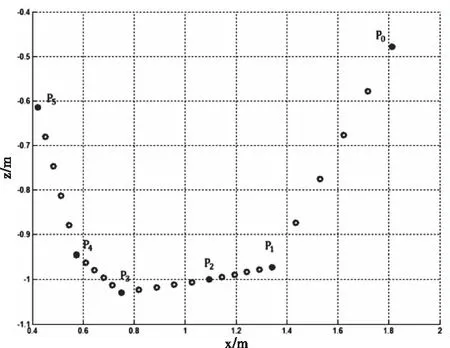
圖6 挖掘機器人基坑挖掘軌跡圖

5.3 仿真結果分析

三種不同算法整定下系統的單位階躍響應如圖8所示。經過三種不同算法整定后的PID參數和適應度最優(yōu)值如圖7所示。從圖8可以得出：三種不同整定算法曲線的變化趨勢基本相同，均沒有超調現象出現，標準PID算法整定后系統的響應速度較慢，調節(jié)時間較長，系統的控制效果差。標準遺傳算法和遺傳螢火蟲算法整定后的系統，在調節(jié)時間和響應速度方面都都得到了較大的提高。經過遺傳螢火蟲算法整定后的系統響應速度最快，上升時間和調節(jié)時間也都最小。表明遺傳螢火蟲算法可以更有效的對PID參數進行整定，提高系統的控制精度。

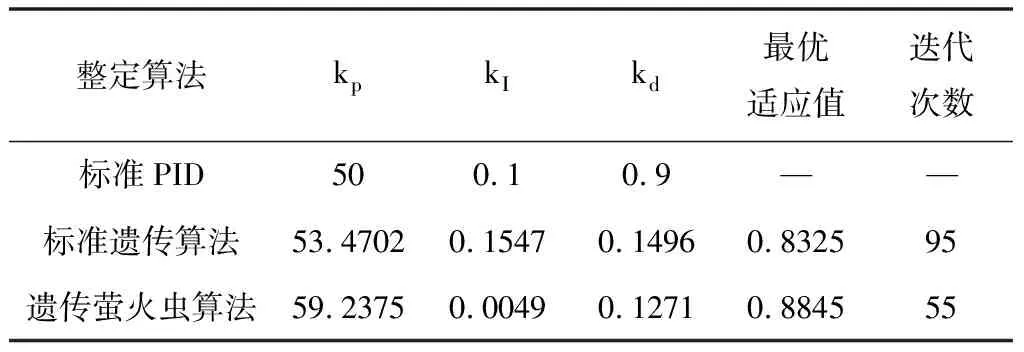
整定算法kpkIkd最優(yōu)適應值迭代次數標準PID500.10.9——標準遺傳算法53.47020.15470.14960.832595遺傳螢火蟲算法59.23750.00490.12710.884555

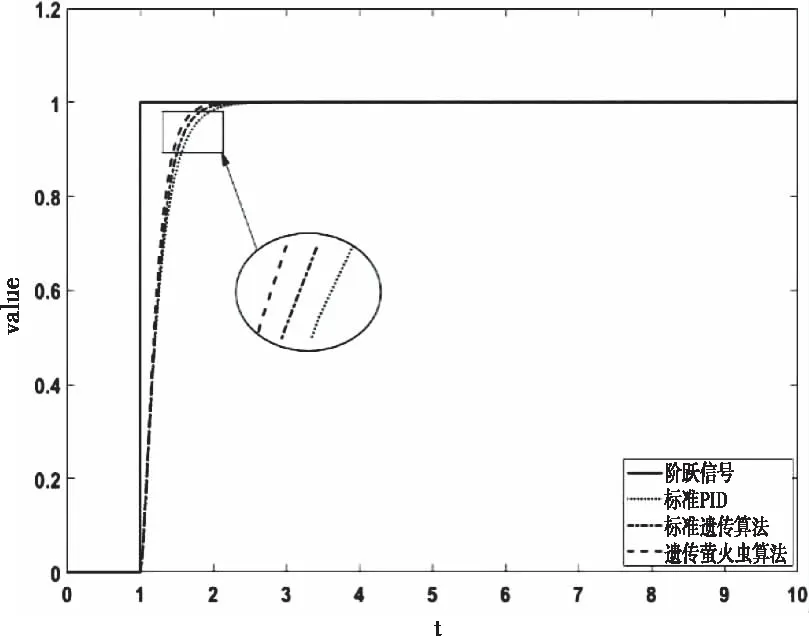
圖8 三種算法的階躍響應對比圖

三種不同算法整定下系統的正弦響應如圖9所示。從圖9可以得出：三種整定算法的響應跟蹤曲線都有遲滯現象，其中遺傳螢火蟲算法整定方法的跟蹤誤差最小，發(fā)生遲滯的時間也最短，表現出了較優(yōu)的動態(tài)特性。

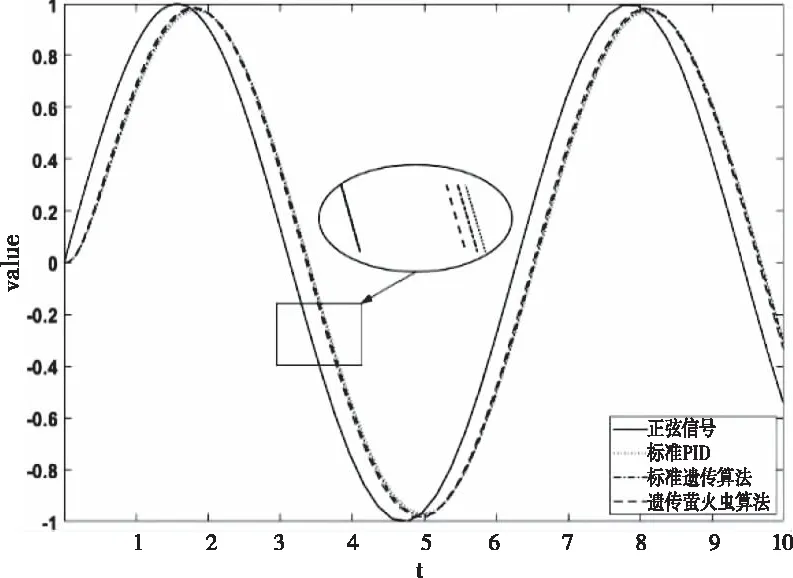
圖9 三種算法的正弦響應對比圖

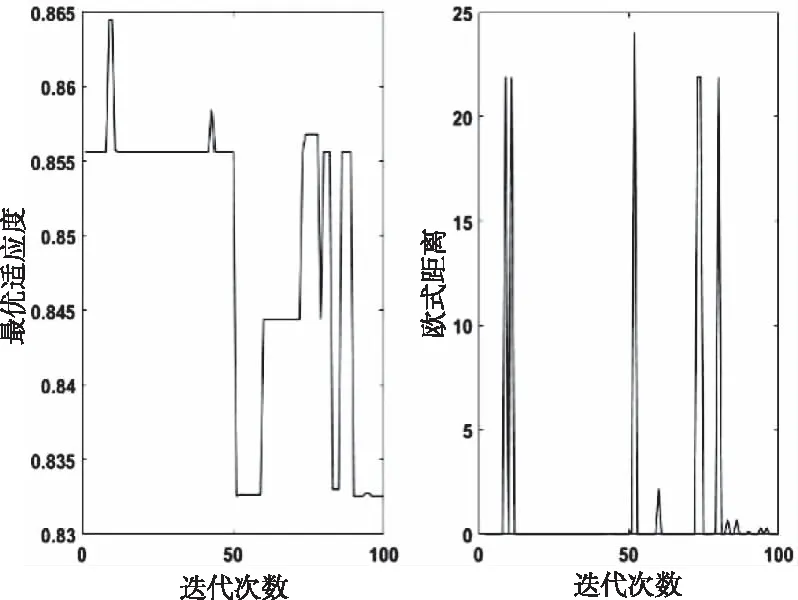
圖10 標準遺傳算法最優(yōu)適應度和歐氏距離隨迭代次數變化曲線圖

標準遺傳算法和遺傳螢火蟲算法整定下最優(yōu)適應度和歐式距離隨迭代次數變化曲線如圖10和圖11所示。從圖10和圖11可得出：標準遺傳算法的最優(yōu)適應度是隨著迭代次數的增加而減小的，且收斂速度較慢，直到進化到第95代才獲得最優(yōu)適應度，歐氏距離也在快達到最大迭代次數時才逐漸減小為0。遺傳螢火蟲算法的最優(yōu)適應度是隨著迭代過程的進行而持續(xù)增加的，在進化到第55代就達到了最優(yōu)，且歐氏距離也在第55代開始就恒等于0，提前滿足了算法停止準則，有效的縮短了算法的運算時間，表明遺傳螢火蟲算法大大提高了收斂速度和尋優(yōu)精度。

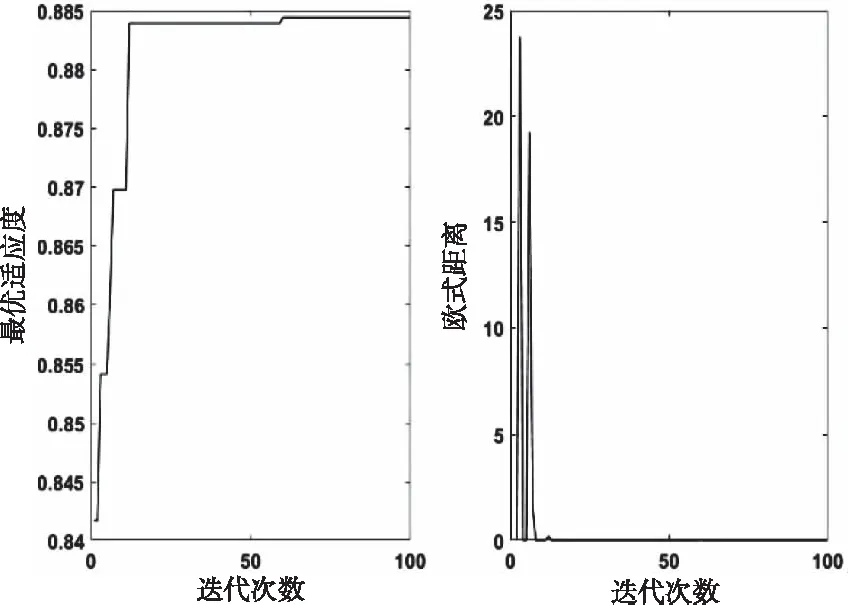
圖11 遺傳螢火蟲算法最優(yōu)適應度和歐氏距離隨迭代次數變化曲線圖

標準遺傳算法和遺傳螢火蟲算法整定過程中PID參數的變化曲線如圖12和圖13所示，能夠看到PID參數在遺傳螢火蟲算法整定過程中變化不大，且能夠較早的達到全局最優(yōu)值，表明遺傳螢火蟲算法具有較強的參數尋優(yōu)能力，還有效的解決了標準遺傳算法在整定過程中參數容易陷入局部最優(yōu)的問題。

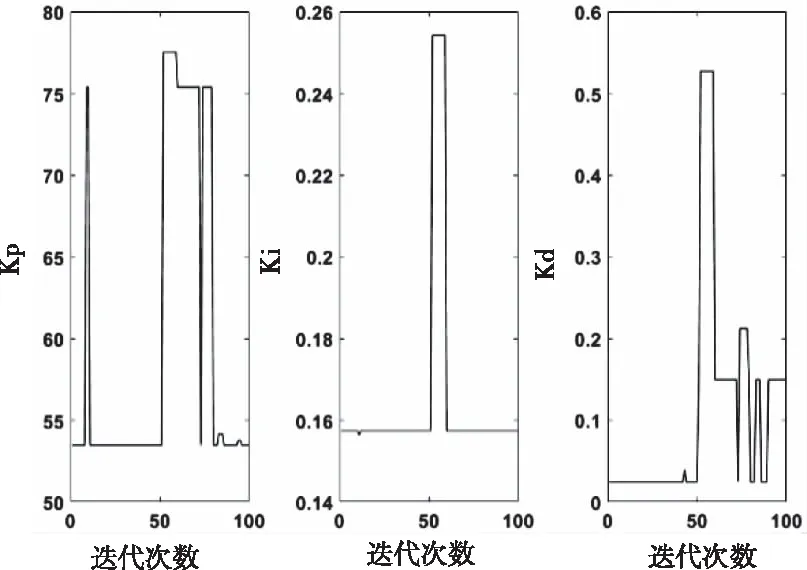
圖12 標準遺傳算法整定PID參數變化曲線圖

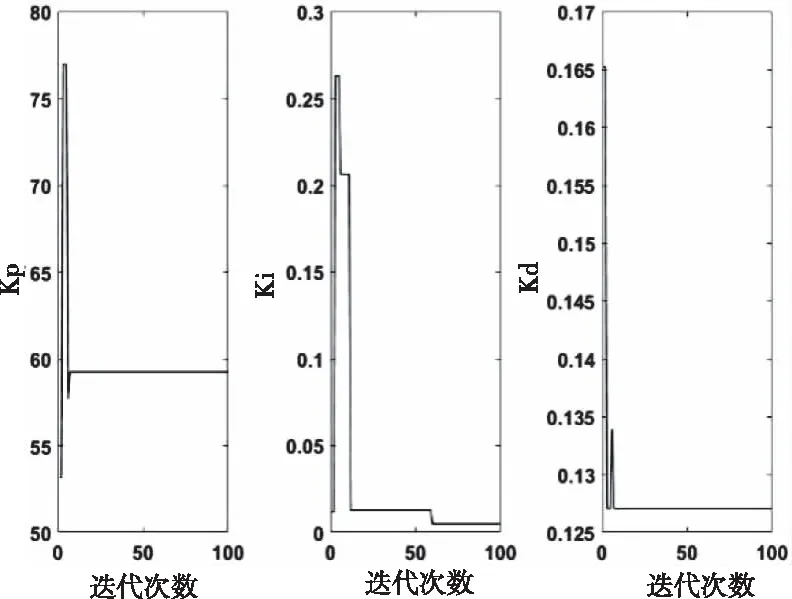
圖13 遺傳螢火蟲算法整定PID參數變化曲線圖

三種不同算法整定下控制系統對規(guī)劃的目標鏟斗關節(jié)軌跡跟蹤曲線如圖14所示。實際上由于從控制器發(fā)出指令信號到鏟斗關節(jié)開始運動，這之間會存在延遲，所以圖中跟蹤曲線不能在一開始就對目標軌跡進行跟蹤。從圖1中可以看出，使用標準遺傳算法和遺傳螢火蟲算法可以有效減小對目標鏟斗關節(jié)軌跡的跟蹤誤差，其中遺傳螢火蟲算法作用明顯，跟蹤響應速度最快，與目標軌跡的跟蹤誤差最小。表明了遺傳螢火蟲算法在鏟斗關節(jié)軌跡跟蹤方面的良好性能，同時也說明遺傳螢火蟲算法在挖掘機鏟斗位置控制方面的有效性。

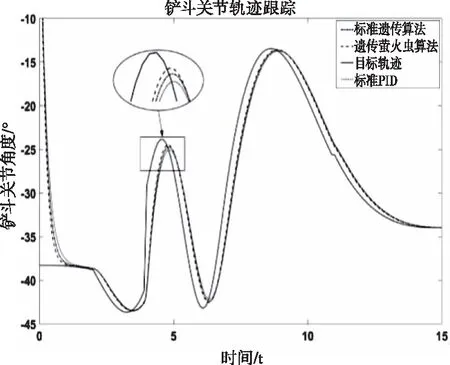
圖14 鏟斗關節(jié)軌跡跟蹤曲線圖

6 結論

提出一種遺傳螢火蟲算法用于挖掘機電液伺服控制系統PID控制器參數的整定。在標準遺傳算法的基礎上設計了改進的交叉算子和自適應調整的非線性交叉概率和變異概率；將人工螢火蟲算法引入遺傳算法中；并提出遺傳螢火蟲算法歐氏距離停止準則。仿真結果表明，遺傳螢火蟲算法能夠有效提高控制系統的響應速度和動態(tài)特性，大大提高了算法的收斂速度和尋優(yōu)精度，并且解決了容易陷入局部最優(yōu)的問題，強化了算法的全局尋優(yōu)能力，系統的魯棒性也更好。從設計的挖掘機器人鏟斗關節(jié)軌跡跟蹤仿真可知，遺傳螢火蟲算法在鏟斗關節(jié)軌跡跟蹤方面有著良好的性能，表明遺傳螢火蟲算法在挖掘機鏟斗位置控制方面的有效性，這對于研究液壓挖掘機智能化挖掘有一定的理論指導意義。