基于有限元應力的三維邊坡穩定分析系統

韋立德，劉文連，陸得志，李江龍

(1. 中國科學院武漢巖土力學研究所，湖北 武漢 430071；2. 中國有色金屬工業昆明勘察設計研究院有限公司，云南 昆明 650051)

1 引言

自然界發生的滑坡絕大多數呈三維形態，越來越多的工程實際提出了建立三維邊坡穩定分析的要求。三維邊坡穩定分析可以更加真實地反映邊坡的實際形態，特別是當滑裂面 已經確定時，使用三維分析可以恰當地考慮滑體內由于滑裂面的空間變異特征對邊坡穩定安全系數的影響。邊坡穩定性分析方法有多種，但應用最為廣泛和有效的主要有兩種，即基于剛體極限平衡理論的傳傳統計算方法具有簡單、方便、快速的特點，目前二維剛體極限平衡法已經成熟，在邊坡方面應用較為廣泛，且三維剛體極限平衡法在工程上也得到了應用[1-4]。然而，傳統計算方法在條間力、滑動面上假設過多，且不考慮邊坡的應力-應變關系，所得到的底滑面上的力不盡符合實際，也不能求得邊坡本身的變形對邊坡變形及穩定性的影響。有限元法不僅滿足力的平衡條件，而且還考慮了應力、變形關系，能夠得到邊坡在荷載作用下的應力、變形分布，所得到坡體的應力、應變與實際情況比較接近，比剛體極限平衡法更為精確合理[4，5]。有限單元法在分析邊坡計算安全系數時的困難之一是如何將有限元計算的結果轉化為工程上適用的安全系數。目前有兩類基本的有限元方法，即建立在強度折減基礎上的有限元法和建立在滑裂面應力分析基礎上的有限元法。強度折減法因通過計算能同時得到邊坡體安全系數及臨界滑面位置，因此在工程實踐中得到了較廣泛的應用。然而該方法需要反復試算，在接近極限狀態時，收斂很慢，尤其對于復雜的三維動力問題，其計算時間讓人無法忍受。除此之外，由于影響強度折減法的因素較多，到目前為止，還沒有一種被工程界和學術界都廣為接受的通用標準，一定程度上限制 了該方法在實際工程中的廣泛應用。建立在滑裂面應力分析基礎上的有限單元法，是在邊坡中定義一個潛在的滑裂面，根據有限元得出的應力分布，計算滑裂面上各點應力水平，再定義安全系數；基于有限元計算的三維邊坡滑裂面搜索方面有一定的研究[5-10]，但主要采用遺傳算法等方法搜索且搜索變量個數比較少，當前邊坡工程商業軟件往往采用窮舉法搜索因為普遍認為該法更可靠[11]，基于有限元計算的三維邊坡滑裂面搜索方法在易行性、應用于復雜工程方面還有待于進一步地研究和完善。

本文作者曾致力于基于有限元計算的邊坡三維滑裂面搜索方法及工程應用探索[12]，本文是該工作的一部分。本文建議了一個更加易行的三維邊坡分析系統，總結基于有限元計算的邊坡三維滑裂面搜索方法，然后用窮舉算法搜索出最危險滑裂面，得出相應的安全系數作為邊坡的安全度評價指標，建議滑動體的Flac3D建模與顯示技術，并研制了基于該法的程序，用于邊坡穩定分析。本文研究成果對三維邊坡穩定性分析與治理具有借鑒意義。

2 安全系數的定義

在此邊坡穩定性安全系數采用基于剪應力計算方法，即坡體沿整個滑動面的安全系數定義為

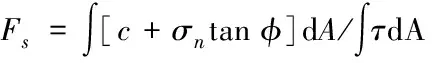
(1)

式中：σn、τ為滑動面上的法向應力和切向主應力；c為材料的黏聚力；φ為材料的內摩察角；A為滑動面的面積。

3 基于有限元軟件計算應力的三維邊坡極限平衡分析方法

利用商業有限元軟件的強大建模能力建立邊坡幾何模型和有限元網格模型，利用商業有限元軟件可以計算有限元網格模型節點多的優勢進行三維邊坡有限元計算，利用有限元計算中的有限元網格和有限元單元應力信息，滑動面采用很多三角形模擬，計算邊坡穩定性安全系數、下滑力和抗滑力，為邊坡穩定評估和加固設計提供依據。

3.1 三維邊坡極限平衡分析系統中邊坡模型構建

由邊坡有限元網構成邊坡幾何模型，由有限元軟件計算單元高斯點應力分布構成邊坡應力場分布。為了更好模擬自然邊坡地質構成的復雜性，邊坡有限元網模型由四面體單元構成，單元高斯點應力為四面體單元的高斯點應力平均值。

3.2 滑動面參數設置和由三角形組成的滑動面構建

對三維問題，一般假設滑動面為橢球面，本文采用此假設，由三個球心坐標和三個半徑6個變量(xi，yi，zi，ai，bi，ci)及滑動角θi共7個變量確定潛在橢球形滑動面，其方程如下面所示

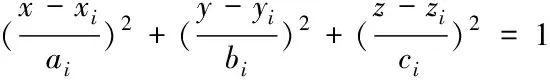
(2)

在確定7個變量變化范圍后基于窮舉算法通過循環語句給出一組組7個具有定值的變量組成的數組，每個數組代表一個潛在橢球形滑動面的確定參數；確定哪個四面體與橢球面相交，基本搜索方案是遍歷有限單元列表，對選定單元的所有邊(線段)的兩個端點坐標(x1,y1,z1)和(x2,y2,z2)帶入橢球面方程，以下列不等式成立表示橢球面與線段相交，滿足選定單元三條線段與橢球面相交表示橢球面與該四面體單元相交，根據交點建立三角形模擬在該選定單元范圍內的潛在滑動面。

(3)

遍歷所有有限單元列表，所有建立的三角形滑動面的集合就是采用的以三角形模擬的對應(xi，yi，zi，ai，bi，ci)和θi確定的滑動面，如圖1所示。

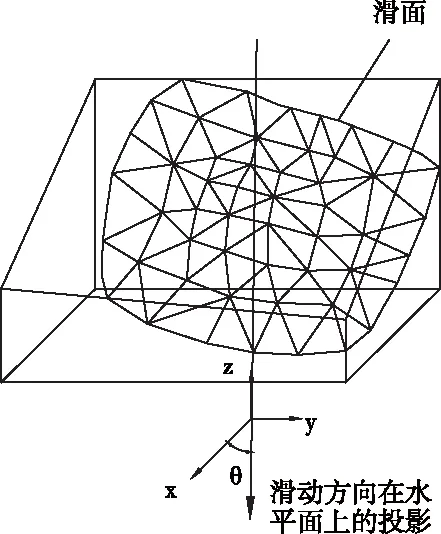
圖1 三維邊坡滑動面和滑動角

3.3 形心所在單元搜索

為求解潛在滑動面應力，首先需要確定潛在滑動面每個三角形形心在哪個單元內。基本搜索方案是遍歷有限單元列表，以確定形心是在當前單元的“內部”或“外部”。如果形心是在“內部”，單元被找到，搜索完成。如果形心是在“外部”，繼續搜索列表中的下一個元素，直到找到包含該形心的單元。在此采用矢量點積法判斷三角形形心是否在某個有限元單元內。對單元的平面定義指向外部的法線向量，三角形形心到該單元平面上任意一節點定義第二個向量，這兩個向量的點積小于或等于0說明三角形形心在單元內部，據此找到三角形形心所在單元。

3.4 滑面三角形內的應力分析

有限元分析結果給的應力是單元高斯點應力，取高斯點應力平均值為單元平均應力。三角形滑面應力近似取為其形心所在有限元單元平均應力。

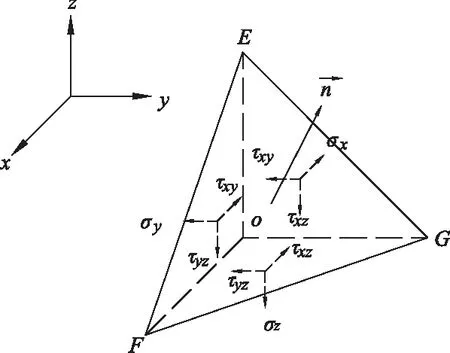
圖2 應力分量圖

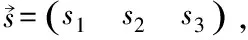
S1=cosθ，S2=sinθ，S3=-cosθ·n1/n3-sinθ·n2/n3

(4.1)

特殊情況在n3=0時，該小滑塊處于豎直方向，那么該滑塊的滑動方向一定在沿z軸負向，那么該滑塊的滑動方向為

S1=0，S1=0，S1=-1，s1=S1/S，s2=S2/S，

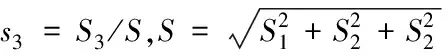
(4.2)

沿著滑動方向的切向應力為ts=txs1+tys2+tzs3。

3.5 安全系數計算

已知組成滑動面的三角形形心處的正應力tn和切應力ts之后，由摩爾-庫侖準則可知，該滑塊的抗滑力為fn=(c+tn·tanφ)A。而該滑塊的下滑力為fs=tsA。通過疊加計算，就可以得到滑面的抗滑力和下滑力，那么，在整個滑面上的安全系數可以表示為

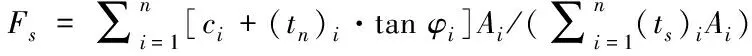
(5)

其中ci和φi分別為滑塊三角形i形心處的凝聚力和內摩擦角，Ai為滑塊三角形i的面積。

3.6 優化計算

采用“窮舉法”進行優化計算，通過使用嵌套 7 個循環并依次改變循環變量xi、yi、zi、ai、bi、ci和θi的值，來搜尋邊坡穩定性安全系數Fn最小值，搜尋到最小值Fn及對應變量xi、yi、zi、ai、bi、ci和θi的值，即為要求解邊坡穩定性安全系數Fn和對應的滑動面。

3.7 滑動體圖形顯示

在獲取含滑面穿過的四面體單元和滑動面內部包含的單元組成的單元集后，即可用該單元集中的每個單元的有限單元信息和包含的節點的坐標編寫出Flac3D的對應該單元的塊體建模語句，對該單元集中的全部單元實施從而完成該單元集Flac3D建模，進而輸入Flac3D建模和利用Flac3D顯示出近似最危險滑動體。

4 程序驗證

本文的方法編入了軟件FEMSTAB3D計算。ZHANG Xing曾發表文章，對一系列具有簡單體形的橢球滑面的三維安全系數提供了解答，本文選用其中一個算例(見圖3)對程序進行驗證。

對此問題采用本文方法FEMSTAB3D計算分析，有限元網格見圖4，只求解(xi，yi，zi，ai，bi)共5個變量解，采用步差為0.25米的窮舉算法求得邊坡穩定性安全系數計算結果為2.074，最危險滑動面球心坐標點對應圖3坐標系的最危險橢球面滑面的球心坐標點是(35.10，28.15)，橢球面在各軸上的截距為：b=69.9，a=c=25.90，滑動體大致如圖5所示。由于如果滑動體只包含滑面范圍以內巖土體的顯示比較麻煩，為了圖顯示方便這里的滑動體把滑面穿過的4面體單元全部包括到滑動體了，因此滑面顯示不是曲面，通過這樣大致滑動體包含滑面穿過的四面體單元和滑動面內部包含的單元。各種方法計算結果見表1，本文方法和其它方法安全系數計算結果一致，在工程上是可以接受的。

表1 各種方法計算得到的安全系數對比

圖3 橢球面邊坡模型

圖4 有限元網格模型

圖5 潛在滑動體

5 工程應用

攀鋼西渣場位于金沙江東岸，在弄溝口北側堆放。渣場邊坡穩定問題較為突出，渣場邊坡的穩定性對攀枝花市的安全意義重大，對渣場邊坡的穩定性分析就非常必要了[12]。渣場高邊坡有限元模型見圖6，該模型模擬了 10種主要的組成材料，其主要參數見表2。本文關注渣場邊坡右半部分(接近下游方向部分)邊坡的穩定性。對此問題采用本文方法FEMSTAB3D計算分析，采用步差為0.25米的窮舉算法搜索到危險滑面為對應球心(630.5，-2.0，115.5)和半徑(63.5，108.0，108.0)的潛在橢圓球滑動體大致如圖7所示，邊坡穩定性安全系數計算結果為1.400，邊坡穩定。對穿過該滑動體的一個剖面采用Slide軟件極限平衡法分析，求得穩定性安全系數為1.321(簡化畢肖普法)。采用開發軟件進行邊坡穩定性安全系數計算結果與采用二維極限平衡法計算結果相差大約6%，分析結果與一般規律一致。

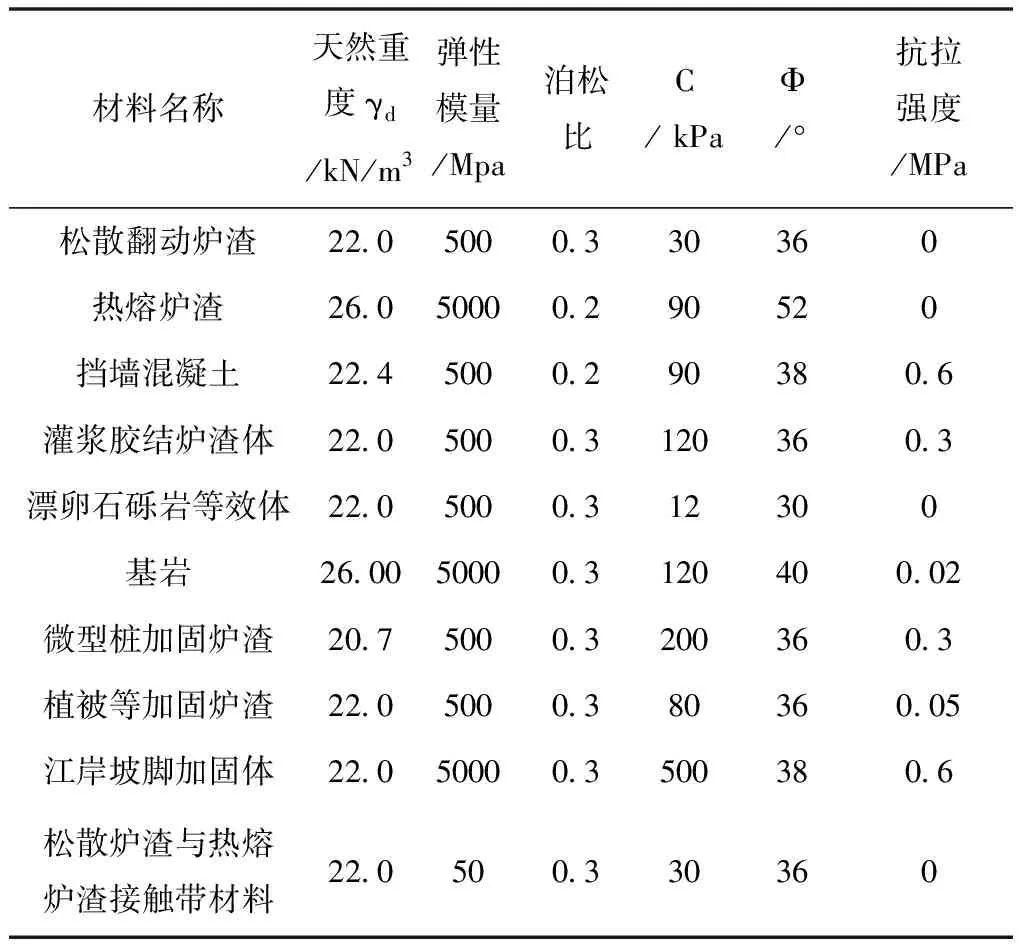
表2 土層摩爾庫倫模型參數

圖6 高邊坡有限元網格模型

圖7 高邊坡潛在滑動體

6 結論

本文建議了一種基于有限元計算的三維邊坡穩定性分析系統，包括穩定性分析方法、顯示技術和程序，通過算例驗證所提系統的可行性和程序的正確性，并以攀鋼西渣場邊坡工程實例驗證所提系統的實用性。計算結果表明，所建議系統是可行的、實用的。和以往類似成果相比，本文的主要創新性或不同之處列舉如下。

1)所建議邊坡穩定性分析系統具有更好的易行性，采用商業軟件解決大模型三維邊坡建模與有限元計算難題，在搜索方法、滑動體顯示技術等方面所建議邊坡穩定性分析系統比類似邊坡分析系統更加簡單、更加易行。

2)首次以復雜的攀鋼西渣場三邊坡工程實例驗證所提系統的實用性。