軸對稱鍛件材料熱力耦合仿真研究

李 龍，溫 毅，康文凱，郝曉華

(1. 中國輻射防護研究院，山西 太原 030006；2. 西南交通大學材料科學與工程學院，四川 成都 610031)

1 引言

鍛件材料要想鑄造成形，成為可被應用的工具需要在高溫、高壓條件的條件下生產，在鑄造的過程中，該材料具有較為復雜的應力及應變狀態[1]，其生產是一個非常復雜的熱力學過程。在生產的過程中，鍛件質量會受到應力、應變、應變速率和溫度變化等因素的影響，要想提高其鑄造質量，需要對相關因素進行嚴格控制[2，3]。

近年來，我國鍛件制造工藝有所更新，但其鑄造的質量始終未取得較好效果，部分學者認為其在胚料成形過程疑似存在缺陷[4]，為提升鍛件鑄造質量，眾多學者采用有限元數值模擬方法對鍛件生產整個過程進行模擬分析，以期能預先發現存在的問題[5-7]。在鍛件材料中，熱剛粘塑性金屬材料[8，9]較為特殊，它的流變應力通常包含應變速率以及變形溫度的函數[10]，使得鍛造成形過程繁瑣，所以更加需要熱力耦合有限元分析來研究這一問題[11]。

本文選取機械繪圖儀作為研究對象，利用剛粘塑性有限元模擬和基于溫度場的有限元模擬，對軸對稱鍛件材料進行熱力耦合分析，用以提升機械繪圖儀軸對稱材料的鍛造工藝。

2 軸對稱鍛件材料熱力耦合模擬分析

2.1 剛粘塑性有限元

在進行鍛件生產時，其塑性形變大于彈性形變，為避免在產生過程中出現鍛造缺陷，利用剛粘塑性有限元數值模擬技術進行改善[12]。剛粘塑性有限元基本理論等同于Markov變分原理。在真實的速度場取以下泛函的極小值用式(1)表示，需要依據速度場同時滿足動可容條件與速度邊界條件。解決體積不可壓縮條件，利用罰函數法，此泛函的一階變分由式(1)表示

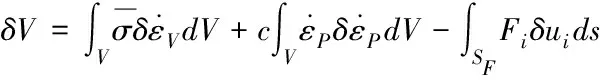
(1)

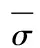
一個存在內熱源的瞬態熱傳導問題由解析鍛件成型進程內的溫度場得到，用以下式(2)表示

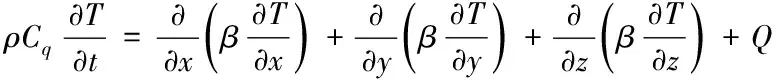
(2)

將式(2)變更為式(3)，利用加權余量法

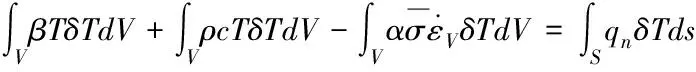
(3)

式中，qn為邊界熱流密度，對流和輻射在工件自由邊界和空氣之間產生，熱傳導在工件和模具之間產生，摩擦接觸邊界產生熱問題。為得知工件內的溫度場，可在結構離散后，對式(3)演變成的微分方程組求解，此方程組與節點溫度相關。為耦合分析熱變形過程，可在實際情況下，依次分開計算增量步內的溫度與變形，通過關聯它們之間的影響來完成。

2.2 基于溫度場計算的有限元數值模擬

內熱源不穩固導熱是鍛件成形過程內溫度場計算的缺陷，采用下列式(4)表示對稱軸鍛件成形過程的溫度場

(4)

上述式(4)中，R為徑向坐標；Z為軸向坐標；CV為材料比熱。需滿足下列條件，用來分析熱力耦合溫度場

用式(5)表達在ST上的第一類邊界條件

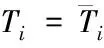
(5)

用式(6)表達在SQ上的第二類邊界條件

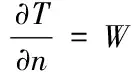
(6)

用式(7)表達在SH上的第三類邊界條件

(7)

用式(8)表達在SC上的接觸換熱條件

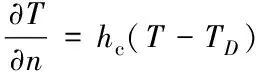
(8)

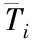
泛函溫度場可依據SH面上的輻射條件與SC面上的摩擦條件，用以下式(9)表示

(9)

式中，σ為玻爾茲曼常數，μ為輻射系數，Wf為摩擦引起的熱流，用以下公式計算Wf

Wf=mk|uS|

(10)

利用Galerkin法將式(10)進行離散化，獲得以下式(11)

(11)

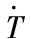
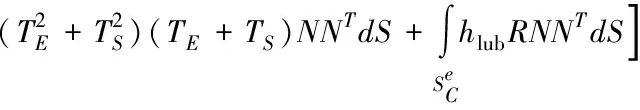
(12)

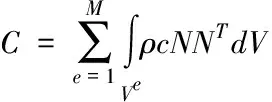
(13)

(14)

式(12)-(14)中，單元總數用M描述，形狀函數矩陣用N表示，形狀函數的微分用L表示，即Lij=Ni，j，SH邊界上的溫度用Ts表示。式(12)右邊的四項依次是貢獻給K的熱傳導、熱對流、熱輻射和接觸邊摩擦。式(14)右邊的五項依次是貢獻給Q的塑性功、熱流密度、接觸邊摩擦、熱對流和熱輻射。利用兩點差分法將T展開

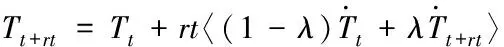
(15)

(16)

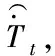
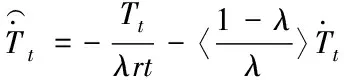
(17)

將式(16)引入式(11)，可得知式(18)

(18)

增量求解瞬態溫度場有限元方程就是式(18)。

2.3 鍛件材料熱力耦合分析

進行熱力耦合步驟：

1)計算初始速度場u0，假定初始速度場u0存在于已獲知的初始溫度場T0。

3)對速度場u1進行計算，它與溫度場T0對應。

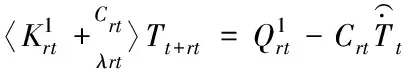
(19)

7)達到收斂速度場與溫度場，需對步驟5)、步驟6)進行反復。

8)對當前時間步的應變速率張量、應力張量、等效應力以及等效應變等相關參數進行計算，需再此之前將節點坐標和等效應變值進行更新。

10)反復步驟3)至9)直至預計的變形結束，再此之前需添加一個時間增量。

3 熱力耦合模擬實驗分析

挑選不同的工藝參數，有限元模擬計算機械繪圖儀軸對稱鍛件材料在不同工藝條件下的精鍛過程。分析不同變形速度在變形過程中對溫度的影響，變形速度選取55mm/s、40mm/s、25mm/s，在同一壓下量下，分析材料溫度變化情況，實驗結果如圖1所示。

圖1 不同變形速度下鍛件材料最高/最低溫度變化

分析圖1可知，在相同壓下量時，變形速度越高，溫度越高，最高溫度大幅升高，會產生較大的溫度變化，當變形速度越小時最高溫度和最低溫度形成的溫度差越小，因此選取較低的變形速度更適合鍛造機械繪圖儀軸對稱鍛件材料。

分析不同大小的摩擦因子在變形過程中對溫度的影響，摩擦因子選取0.25、0.35、0.45，在同一壓下量下，隨著壓下量的增加摩擦因子引起溫度產生的變化，實驗結果如圖2所示。

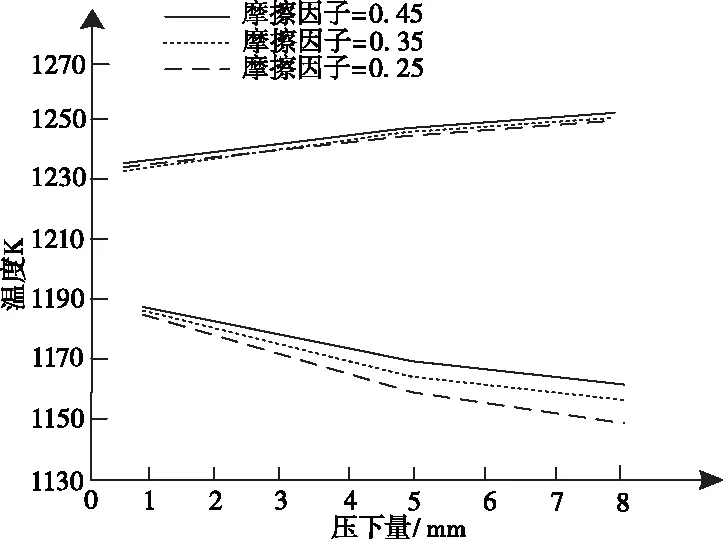
圖2 不同摩擦因子下鍛件材料最高/最低溫度變化

由圖2可知，摩擦因子的變化幾乎不影響鍛件材料的最高溫度，因為摩擦因子增大，會產生摩擦熱，但最低溫度因摩擦因子的減少而出現大幅下降，因此鍛造機械繪圖儀軸對稱鍛件材料應選擇較高的摩擦因子。

選取不同胚料溫度1129K、1156K、1202K，分析胚料溫度在同一壓下量下，最大/最小等效應力差的變化，實驗結果由圖3表示。

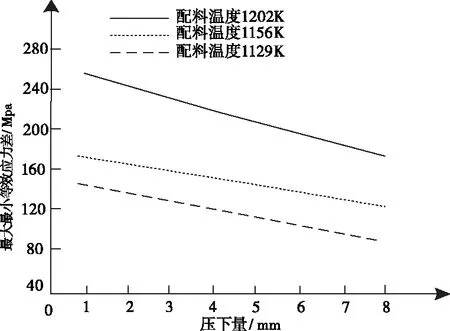
圖3 不同鍛造胚料溫度下材料最大、最小等效應力差變化

分析圖3可知，鍛造胚料溫度的不同，最大/最小等效應力差也發生了變化，不同溫度的胚料隨著壓下量的增加最大最小等效應力差都逐漸降低，胚料溫度越高，最大最小等效應力差也越小。

相同壓下量下不同胚料溫度對變形力的影響結果由圖4表示。

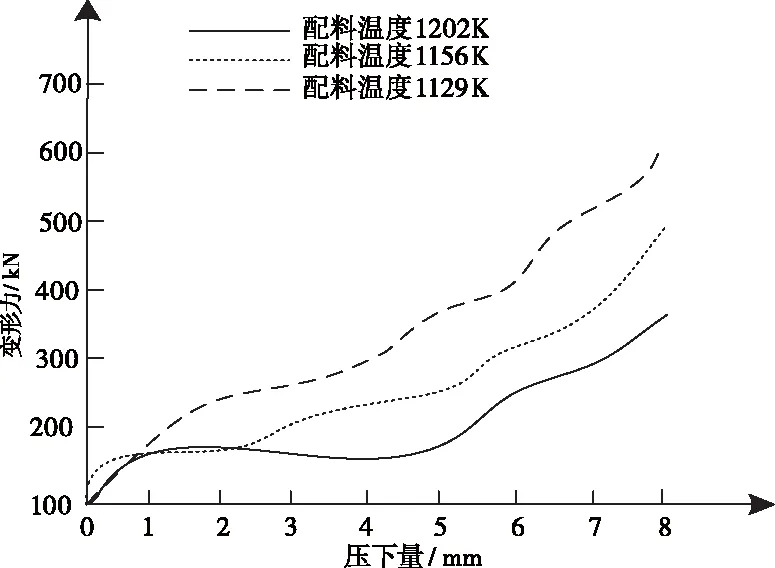
圖4 不同胚料溫度下載荷-形成曲線

分析圖4可知，由于胚料溫度的不同，變形力在不同壓下量下逐漸增加，但胚料溫度越高，變形力增加越小，胚料溫度較低變形力增加最大，因此胚料溫度低更適合鍛造材料。

為檢驗本文熱力耦合模擬分析的正確性，對機械繪圖儀軸對稱鍛件鍛造過程進行有限元模擬計算，選取三個測試點A、B、C，對比本文熱力耦合模擬分析得出的溫度值與各測試點的實測溫度值，實驗結果如圖5所示。

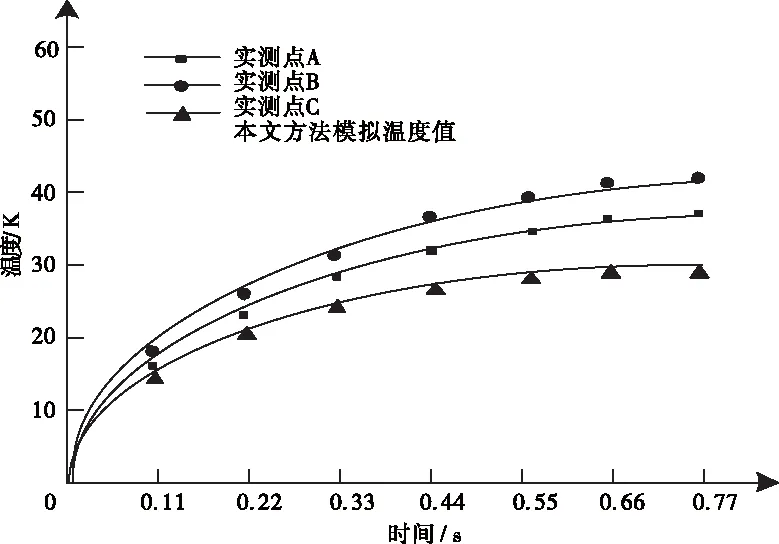
圖5 各測試點溫度模擬結果

由圖5可知，本文熱力耦合模擬分析得出的溫度值與各實測點溫度值非常接近，隨著時間的變化，本文計算結果并沒有與實測溫度值相差過大。

4 結論

本文采用剛粘塑性有限元模擬與基于溫度場的有限元模擬對用于機械繪圖的軸對稱鍛件材料鍛造過程進行熱力耦合實驗，對不同變形速度、摩擦因子等因素對最高最低溫度變化的影響進行分析，研究不同鍛造胚料溫度下最大最小等效應力差變化及對變形力的影響，并且還將熱力耦合有限元分析溫度值與實際測試點溫度對比，得出計算結果與實測溫度的關系。實驗表明：熱力耦合有限元分析溫度值與實測點溫度值相近，在進行鍛造軸對稱鍛件時，適合采用較低變形速度、較高的摩擦因子，同時鍛造胚料更適合較低的鍛造溫度。