基于壓縮感知的自適應再選擇毫米波信道估計

李澤丕，李春樹，李佳寧，劉 煜

(寧夏大學物理與電子電氣工程學院，寧夏銀川 750021)

1 引言

隨著無線通信技術的快速發展，越來越多智能終端的應用，對無線通信系統的網絡容量提出了更高的要求。利用高頻段的毫米波進行無線通信是解決頻譜資源緊張的有效方法之一[1]。毫米波具有豐富的頻譜資源和顯著的多普勒頻移等優點。毫米波技術能夠與大規模 MIMO (Massive Multiple Input Multiple Output)技術和超密集蜂窩網絡(Ultra Dense Network，UDN)等關鍵技術互補使用，具有廣闊的應用前景[2-3]。但毫米波的多徑數目、衰落特性、散射特性等與微波通信有顯著區別[4-5]，現有微波頻段通信系統的信道建模、信道估計、預編碼等理論通常不能直接應用于毫米波通信系統[6]。因此，對毫米波系統進行精確的信道估計就顯得至關重要。

在信道估計方法中，最小二乘法(Least squares，LS)將估計問題作為確定性的最優化問題來處理，盡管可以完整地估計信道，但其未能有效地利用信道特性[7-8]。毫米波由于其衰落特性，使其信道具有稀疏性，而壓縮感知理論方法在解決稀疏信號重構問題上，具有計算高效、準確性高的特點[9]。文獻[10]針對毫米波系統的稀疏特性，利用壓縮感知正交匹配追蹤(Orthogonal Matching Pursuit，OMP)算法對其進行信道估計，與傳統的最小二乘法相比，使用更少的導頻信號獲取信道的狀態信息，但是OMP 算法依賴于信號的稀疏度。文獻[11]在StOMP算法的基礎上引入兩個系數，分別用來向上和向下調整閾值，可以根據稀疏度來進行閾值的動態調整以達到自適應地進行信道估計，但其依賴信道的稀疏度作為先驗信息。文獻[12]在第一次選取的多個原子中，通過對所選原子的模長進行比對，刪除部分原子，根據估計結果再次對所選原子進行篩選，最后根據殘差判斷是否錯誤刪除，否則返回上一次迭代，存在估計性能與估計速度無法兼顧的問題。稀疏度自適應匹配追蹤算法 (spa-rsity adaptive matching pursuit，SAMP)通過步長S不斷逼近稀疏度進行重構，文獻[13]采用基于SAMP的回溯步長算法，在過估計時返回上一次迭代并采用小步長將引起過估計的大步長替代。

文章提出的Ts-StOMP算法，在每次迭代過程中選取多個原子，不同于每次選取一個原子的OMP算法，其估計速度更具優勢，同時避免了OMP算法需要稀疏度作為先驗信息的問題。該算法在StOMP算法每次選取多個原子的基礎上，利用sigmoid函數對所選原子的最小二乘結果進行比對，對所選原子進行二次篩選，達到自適應再選擇的目的。不但避免了文獻[13-14]中因為步長選取所導致的大步長過估計問題，而且保障了估計精度。

2 毫米波稀疏信道模型

文章基于毫米波窄帶下行信道模型，發送端和接收端均采用均勻線性陣列，如圖1所示。

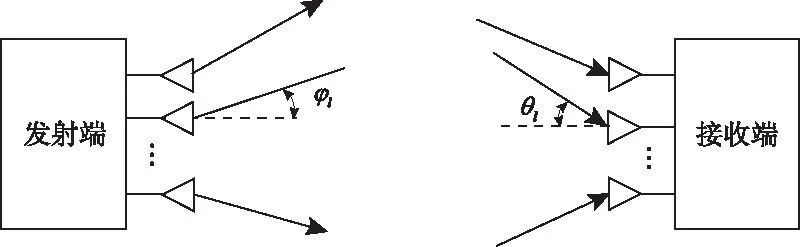
圖1 均勻線性陣列

φl和θl分別為第l條路徑的離開角和到達角。在該陣列中，陣元等間隔分布，間隔為d。發射端和接收端的天線數量分別為Nt、Nr，則系統的信道矩陣H可以表示為

(1)

將信道矩陣H改寫為

(2)

令Ar=[ar(θ1)，ar(θ2)，…，ar(θL)]，則有

(3)

發送端和接收端均采用均勻線性陣列的毫米波信道矩陣H可簡寫為

(4)

其中Ha∈CL×L為信道復增益矩陣，At∈CNt×L、Ar∈CNr×L分別為發送端和接收端的均勻線性陣列矩陣。

3 毫米波通信系統模型

在毫米波系統中，相比于全數字波束成形和純模擬波束成形結構，混合波束成形更具有實際的應用價值[15]。文章采用混合波束成形(Hybrid analog and digital beamforming，HBF)部分連接結構，減少了射頻鏈路數，降低了硬件實現的復雜度。

詳細系統模型如圖2所示。

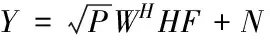
(5)

向量化式(11)得

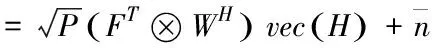
(6)

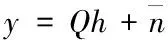
(7)

信道信息h∈CNtNr×1具有稀疏性，即h中有個別非零元素或近似為零。文章定義觀測矩陣Q∈CNsNs×NtNr，y∈CNsNs×1是接收端接收的信號，即在觀測矩陣Q下的觀測值，進而可以由觀測值y利用壓縮感知理論求解h的最優化問題。

圖2 毫米波通信系統模型

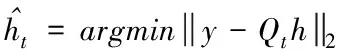
(8)

(9)

求解時的貪婪算法多采用正交匹配追蹤(Orthogonal Matching Pursuit，OMP)算法和分段正交匹配追蹤(StagewiseOrthogonal Matching Pursuit，StOMP)算法等，文章主要研究分段正交匹配追蹤算法。

4 改進的自適應迭代算法

OMP算法在每次迭代過程中，由于每次只選出一個原子，估計速度較慢。StOMP算法相比于OMP算法，雖然不需要稀疏度作為先驗信息，每次選取多個原子，加快了估計速度，但穩定性較差。OMP算法和StOMP算法存在估計速度和穩定性不能兼顧的問題。

文章基于StOMP算法，不依賴完備的先驗信息，利用StOMP算法得到的估計值，使用sigmoid函數Ut，對已選擇的多個原子進行二次選擇。sigmoid函數在t≥0時，Ut∈[0.5，1)，具有非線性遞增的特性。迭代開始時，函數值Ut較小，使得前期迭代可以選出多個原子，增加估計速度，隨著迭代次數的增加，函數值Ut接近于1，二次選擇的原子數目逐漸變少，實現小步長精確逼近。Ts-StOMP算法相比于StOMP算法，能夠提高估計性能，相比于OMP算法，能夠加快估計速度。詳細步驟如下：

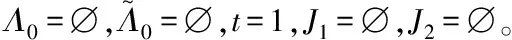
輸入：觀測矩陣Q，觀測向量y，閾值參數ts，最大迭代次數T。

輸出：稀疏信號h的估計值。

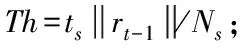
2)判斷J1=?，若J1=?，返回1)；若J1≠?，繼續3)；

3)更新索引集Λt=Λt-1∪J1，記錄找到的感知矩陣中的重建原子，并入集合Qt，Qt=Qt-1∪qj，j∈J1；

8)判斷t>T。若t>T，則停止迭代，=t2；若t≤T，執行1)。

5 仿真結果及分析

對毫米波系統進行信道估計，取發射端天線數目Nt=64，接收端天線數目Nr=16，天線間距離d=λ/2。仿真次數均在5000次以上。為比較OMP算法、StOMP算法和Ts-StOMP算法的估計性能，采用歸一化均方誤差(Normalized Mean Square Error，NMSE)作為衡量標準。

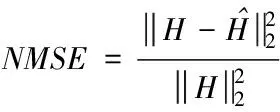
(10)

取稀疏度L=8，不同信噪比時三種算法的估計性能如圖3所示。

圖3 不同SNR下的性能對比

隨著SNR的增大，三種算法信道估計的NMSE越小，估計精度越高，性能越好。在低信噪比的情況下，改進的Ts-StOMP算法估計性能明顯優于OMP和StOMP算法。

由于在低信噪比下，Ts-StOMP算法具有顯著優勢，而當SNR>15dB時，三種算法有著相近的估計性能。故取SNR=15dB，對三種算法進行不同稀疏度下的仿真，如圖4所示。

圖4 不同稀疏度下的性能對比

在不同稀疏度的情況下，Ts-StOMP算法整體性能優于OMP算法，且估計性能最穩定。在L<4時，StOMP算法性能略優于Ts-StOMP算法。隨著稀疏度的增大，需要更多的測量向量來恢復信號，三種算法信道估計的NMSE也在增大，估計性能降低，但Ts-StOMP的估計性能明顯優于OMP和StOMP算法。

仿真50000次，對三種算法在不同稀疏度情況下的仿真時間進行對比，見表1：

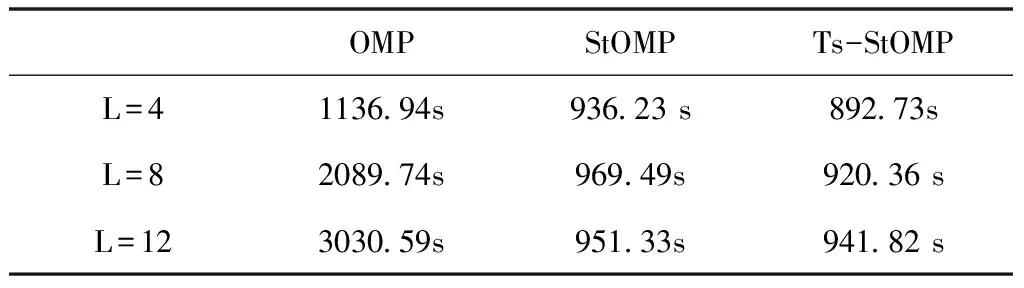
表1 SNR=15dB時運行時間對比

OMP算法依賴于稀疏度作為先驗信息，運行時間會隨著稀疏度的增加而增加。StOMP和Ts-StOMP算法不依賴稀疏度且運行時間遠小于OMP算法，其中，Ts-StOMP算法運行速度略優于StOMP算法。

6 結論

文章研究了毫米波系統的下行信道估計問題，使用sigmoid函數，提出了一種基于分段正交匹配追蹤算法的改進算法，分別在稀疏度相同信噪比不同和信噪比相同稀疏度不同的情況下，將三種算法進行仿真對比估計性能，并記錄運行時間，可以得出以下結論：

1)Ts-StOMP算法不需要稀疏度作為先驗信息，解決了毫米波信道稀疏度不確定時的信道估計問題。

2)當SNR=15dB時，Ts-StOMP算法估計性能略優于其它兩種算法；當SNR<15dB時，隨著SNR的減小，Ts-StOMP算法與其它兩種算法的性能差距逐漸增大，具有更高的穩定性。

3)當SNR=15dB，L=12時，Ts-StOMP算法運行時間約為OMP算法的三分之一，比StOMP算法快9.51秒，具有最快的運行速度。