BB分布信道下基于網絡編碼的參數調優算法

韓曉冬，張立煒，閆富榮

(1. 中國科學技術部信息中心，北京 100862；2. 北京中電普華信息技術有限公司，北京 100085)

1 引言

以空天信息網絡為代表的無線多跳網絡信道環境具有高動態性和高隨機性，網絡拓撲變化性大，極易造成丟包，無法達到網絡的最大通信容量。現有文獻大多針對確定性的丟包率進行研究[1-12]，缺少針對隨機性刪除信道模型下的數據傳輸可靠性研究。如文獻[1]和文獻[12]就是基于刪除概率服從確定的獨立同分布伯努利(Bernoulli)隨機變量研究網絡容量，但是確定性刪除概率信道模型是基于理想化的網絡場景提出的，不適用于實際的復雜網絡環境，尤其是像空天信息網絡這種高動態的隨機性刪除信道模型。此外，由于數據包傳輸不像符號傳輸具有同步性，本質上假設網絡中每條信道上的數據包傳輸服從統一分布也具有一定的局限性。因此，為了更加準確地貼近實際的空間網絡環境，文章建立了BB分布刪除信道下基于隨機線性網絡編碼的參數調優模型，研究貝葉斯學派中具有相關性 Bernoulli隨機變量和的分布下的網絡通信性能。

2 Beta-Binomial分布下基于線性網絡編碼的參數調優傳輸模型

圖1 采用空時網絡編碼的中間節點

假設在某個時隙內每條邊即信道的刪除概率為Pe，因此p=1-Pe表示數據包的成功接收概率，它是一個隨時間變化的服從Beta(α，β)分布的隨機變量，則此時在成功接收概率p下觀測到的樣本分布即似然函數P(Xi=x|p)，其中Xi|p是服從二項分布Binomial(M，p)的隨機變量[14，15]，如式(1)。由共軛分布和先驗信息的知識可知，Xi是一個服從Beta-Binomial(M，α，β)分布的隨機變量，因此根據貝葉斯公式可以求出P[Xi=x]在先驗信息f(p)下的概率分布，如式(2)所示，那么在M個時隙內每個編碼塊通過邊ei∈E成功傳輸的數據包數量Xi應該是一個對式(2)求累加和的統計均值，即式(3)，因此根據文獻[15]和[16]可以得出網絡容量為式(4)。

p～Beta(α，β)

Xi|p～Binomial(M，p)

Xi～Beta-Binomial(M，α，β)

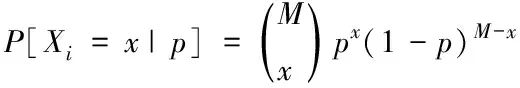
(1)

(2)

(3)

C=E{mint∈T{mincut(s，t)∑ei∈CXi}}

(4)

3 實驗結果與分析

本節主要在Beta-Binomial分布信道下對基于隨機線性網絡編碼的參數調優算法進行分析。根據式(2)的分析可知，信道能成功接收數據包的概率p的先驗信息所服從的Beta分布中超參數α和β會對概率P[Xi=x]產生影響，即α和β是概率P[Xi=x]的兩個自由度，可以通過調整它們的值來得到合理的概率分布P[Xi=x]，進而得到更加符合實際性能預期的網絡通信容量。在發送數據包訓練集未知的條件下，經驗誤差即損失函數越收斂，則信道成功接收數據包的概率精度越高。

由圖2可知當α和β的值相近且較小時，所得的P[Xi=x]<0.1，即能成功接收到的數據包比例非常小，因此Xi的概率分布并不符合實際信道性能的預期，概率分布函數(Probability Distribution Functions，PDF)不在一個合理的范圍之內，因此為了對參數進行更加合理的估計以及對PDF提供一個更加優化的取值參考，結合圖3和圖4的仿真結果可知，α和β的值相差越大，所得到的信道越符合實際性能預期，信道成功接收數據包的概率p的統計均值越大，即趨近于1，所得的P[Xi=x]概率分布越合理。

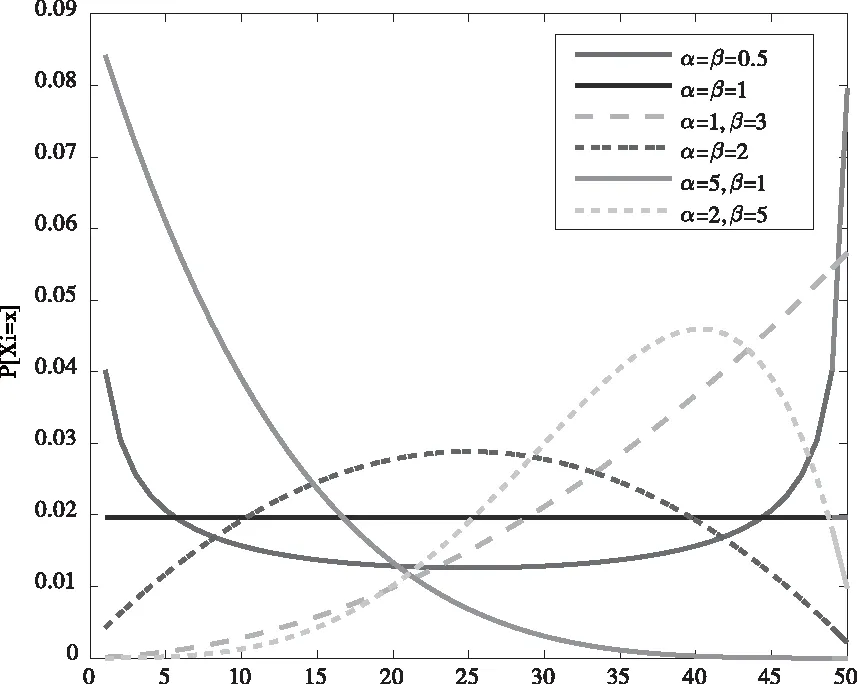
圖2 不同參數設置下的概率分布

圖3的仿真結果顯示P[Xi=x]和β的取值呈負相關，當β～[1，50]時，α越大概率P[Xi=x]的峰值越大，曲線下降得越緩慢，也就是說在M個連續時隙內每個編碼塊通過邊ei∈E所成功傳輸的數據包數量Xi越多。因此在圖3中的藍色五角星曲線是當α=100且βmin=1時，得到此條件下對應的PDF的值為P[Xi=x]max≈0.67，表示在此參數設置下能成功接收的數據包數量最少，相應地信道成功接收數據包的概率p為一個參數為α和β的隨時間變化的Beta隨機變量，則可以得到此條件下M長時隙內p的期望為E[p]=α/(α+βmin)≈0.99，這個值表示貝葉斯統計意義下p的最小值，即信道成功接收數據包的概率為0.99，而相應地信道的刪除概率Pe≈0.01，即在合理的信道估計模型下丟包最多的情況。而在圖3中綠色菱形曲線是當α=500且βmin=1時，得到此條件下對應的PDF的值為P[Xi=x]max≈0.9，表示此時能成功接收到的數據包數量最多，相應地也可以求出此時在時長為M的時隙內p的期望為E[p]=α/(α+βmin)≈0.998，這對應著貝葉斯統計意義下p的最大值，即信道成功接收數據包的概率為0.998，而相應地信道的刪除概率Pe≈0.002，即在合理的信道估計模型下信道丟包最少的情況。

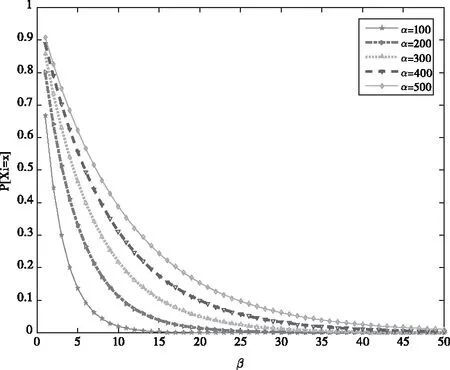
圖下的概率分布

圖4的仿真結果顯示了P[Xi=x]和α的取值呈正相關，當β=1時，α越大概率P[Xi=x]的峰值越大，曲線斜率越小，也就是說在M個時隙內每個編碼塊通過邊ei∈E所成功傳輸的數據包數量Xi越多。在圖4中綠色五角星曲線是當β=5且αmax=500時，得到此條件下對應的PDF的值為P[Xi=x]max≈0.6，表示在此參數設置下成功接收的數據包數量最少，相應地當信道成功接收數據包概率p為一個參數為α和β的隨時間變化的Beta隨機變量時，則可以得到此條件下M長時隙內p的期望為E[p]=αmax/(αmax+β)≈0.99，這個值表示貝葉斯統計意義下p的最小值，即信道成功接收數據包的概率為0.99，而相應地信道的刪除概率Pe≈0.01，即在合理的信道估計模型下信道丟包最多的情況。而在圖4中藍色菱形曲線是當β=1且αmax=500時，得到此條件下對應的PDF的值為P[Xi=x]max≈0.91，表示此時能成功接收到的數據包數量最多，相應地也可以求出此時在時長為M的連續時隙內p的期望為E[p]=αmax/(αmax+β)≈0.998，這對應著貝葉斯統計意義下的p的最大值，即信道成功接收數據包的概率為0.998，而相應地信道的刪除概率Pe≈0.002，即在合理的信道估計模型下信道丟包最少的情況。此情況與圖3綠色菱形曲線中的情況相同，說明基于此信道模型的參數調優算法更加接近實際的網絡鏈路傳輸性能，尤其適用于動態性高的隨機無線網絡環境，此傳輸機制對實際動態網絡環境下的統計信號參數估計具有指導意義，是一種更普適的建模方法和調優算法。

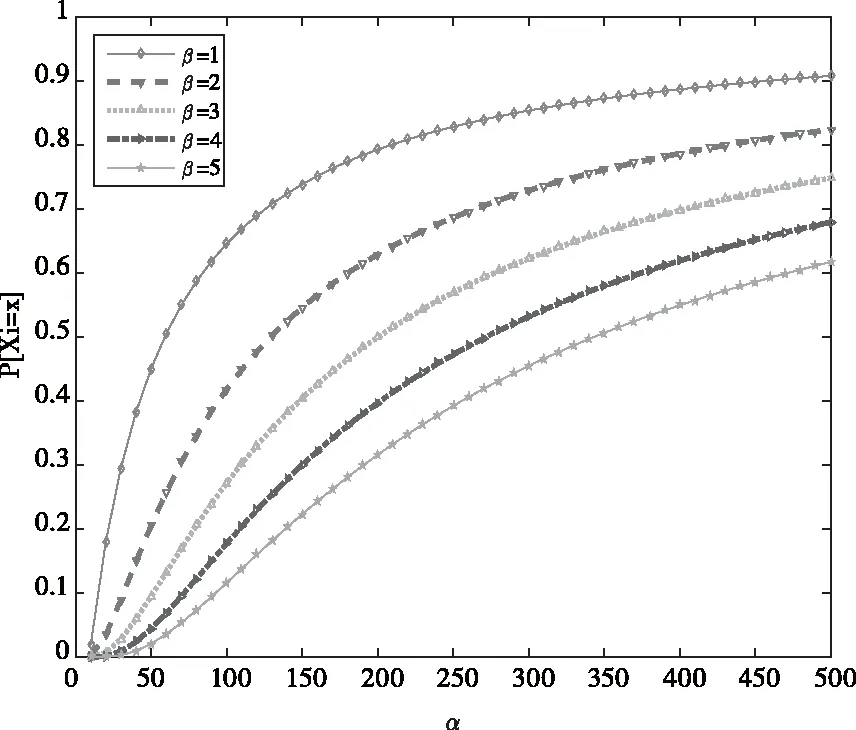
圖時的概率分布

4 結束語

目前數據傳輸機制的可靠性研究主要針對確定性的信道刪除概率，對于隨機性丟包為主的高動態網絡環境不再適用。基于此，本文在Beta-Binomial分布信道模型下提出基于隨機線性網絡編碼的參數調優算法，并進行了理論建模和分析。通過仿真結果可以得出，此參數調優算法適用于動態性高的隨機刪除信道的無線網絡環境，信道可靠性更加接近于實際的網絡鏈路傳輸性能，此數據傳輸機制對實際動態網絡環境下的統計信號參數估計具有指導意義，是一種更普適的建模方法和調優算法。