基于頻域牛頓迭代的水聲頻率估計算法研究

李言勝，張建成，顏 琪，秦正昌

(青島理工大學信息與控制工程學院，山東 青島 266525)

1 引言

水聲頻率估計可廣泛應用于水下定位與導航、水下目標勘探以及運動水聲通信等領域[1]-[6]。常用頻率估計算法多建立在信號離散傅里葉變換(Discrete Fourier Transformation，DFT)基礎上，著重解決柵欄效應[7]問題。Rife等人在文獻[8]中提出雙譜線法，利用信號頻譜主瓣內最大和次大譜線的幅值比例關系插值來進行頻率估計。但當信號真實頻率處于DFT量化頻率附近時，噪聲對次大譜線的影響可能導致插值方向錯誤，增大估計誤差。對此，文獻[9]提出修正算法，加入適當的判決條件進行頻率搬移，再利用雙譜線法得到頻率粗估計值進行迭代，提高頻率估計精度，但是該算法仍具有抗噪性差的缺陷。文獻[10]提出利用信號頻譜中幅值最大的三根譜線修正頻率估計值，但信號頻率位于DFT兩量化頻率之間的中心區域時，該算法精度不高。文獻[11]提出迭代線性預測算法，采用線性預測進行頻率粗估計，反復使用變頻、低通濾波和抽取運算，降低頻率估計信噪比(Signal Noise Ratio，SNR)閾值，提高估計精度，但計算量大。文獻[12]提出將高頻信號搬移到低頻段，低通濾波保留所需頻段，以適當頻率重采樣后進行DFT，達到局部頻譜細化的目的，再進行頻率估計，估計精度較高，但算法整體結構復雜。上述算法大多利用信號頻譜中兩個或多個幅值或相位信息對頻率估計值進行優化，但在SNR較低時，噪聲對信號幅值或相位影響較大，可能導致誤差變大。本文僅利用DFT后的最大譜線進行頻率粗估計，將粗估計值作為牛頓迭代初始值進行兩次迭代，得到最終頻率估計值。該算法結構簡單，低SNR時依然具有良好的穩定性。

2 水聲頻率估計算法原理

定義發射信號為

(1)

其中，A0、f0和φ0分別為發射信號的幅值、頻率和初相位，fs為采樣頻率，N為樣本點數。

經過水聲信道后得到接收信號

n= 0，1，…，N-1

(2)

其中，P為水聲信道多途數，Ap、fp和φp分別為信號通過第p條路徑的幅值、頻率和相位，w(n)為環境噪聲。對r(n)進行N點DFT得

m = 0，1，…，N-1

(3)

定義M為R(m)譜線幅值最大處的抽樣點，即

|R(M)| = max{|R(m)|}

(4)

由f=mfs/N得點M對應頻率值為M，0=Mfs/N，該值即接收信號的頻率粗估計值。將M，0作為牛頓迭代初始值進行頻率精估計，彌補柵欄效應帶來的估計誤差。由(3)得關于頻率f的幅度譜為

(5)

由數學關系得其一階導數G′(f)可近似表示為

G′(f) ≈G′(M，0) +G″(M，0)(f-M，0)

(6)

其中，G″(M，0)為G(f)在M，0處的二階導數，由于接收信號頻譜幅值在真實頻率處應取得極值，因此令(6)右端等于0，得到關于第一次牛頓迭代后的頻率估計值M，1的關系式為

G′(M，0) +G″(M，0)(M，1-M，0)=0

(7)

整理得

(8)

(9)

3 仿真

發射單頻信號，幅度為1V，頻率為9kHz，初相位為0。樣本點數為8192，采樣頻率為120kHz。水聲信道如圖1所示，橫軸表示時間，縱軸表示幅度，信道中含三條多途干擾，分別較直達波延時2ms、5ms和8ms，頻率與直達波相同。

圖1 水聲信道

所提算法多次迭代性能對比如圖2所示，橫軸表示SNR，縱軸表示100次試驗頻率估計值。可看出，所提算法在兩次迭代后已達到良好的估計性能，增加迭代次數，估計性能不再有明顯提升。因此，本文算法采用兩次迭代估計接收信號頻率。

圖2 多次迭代對比

不同算法頻率估計性能對比如圖3所示，橫軸表示SNR，縱軸表示頻率估計值。可看出，SNR較高時，三種算法性能相當，但SNR較低時，所提算法性能更好，即該算法抗噪性更強。

圖3 不同算法對比

4 水箱試驗

2019年11月在青島理工大學進行了水箱試驗，場景如圖4所示。水箱長1.16m，寬0.76m，高0.62m，試驗時換能器與水聽器均保持靜止，布放如圖5所示，收發節點間水平距離為0.4m，深度為0.5m。水箱隨機信道如圖6所示，橫軸表示時域抽頭數，縱軸表示歸一化幅度，可知水箱信道具有強多途干擾。由于試驗過程中換能器與水聽器的相對位置并未改變，所以多途干擾不會使接收信號產生多普勒頻移。

圖4 試驗場景

圖5 換能器、水聽器布放

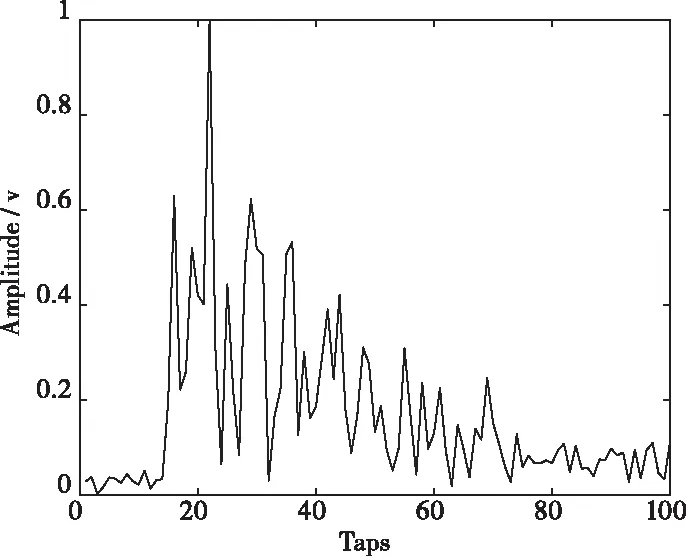
圖6 水箱信道

換能器發射頻率為10kHz的單頻信號，信號持續時長約2.2s，采樣頻率120kHz，水聽器接收信號如圖7所示，橫軸表示時間，縱軸表示幅度。由于收發節點距離較近，環境噪聲較小，因此近似當成無噪聲處理。

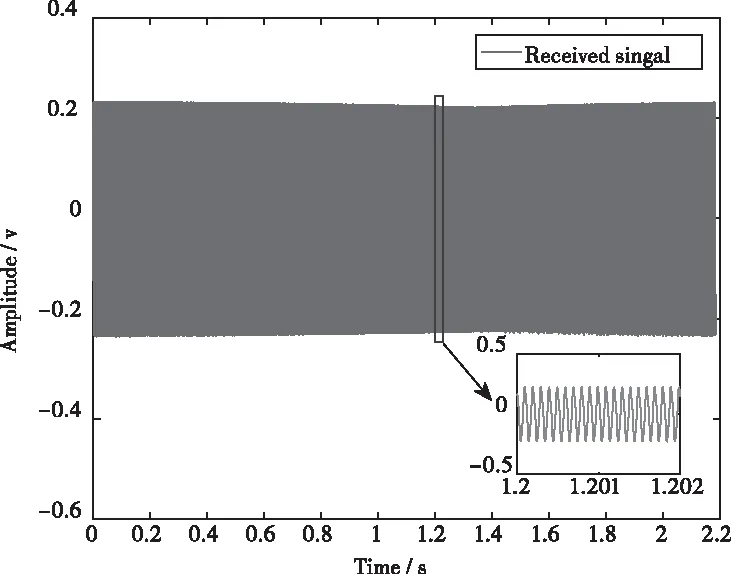
圖7 接收信號

在接收信號中人為加入隨機高斯白噪聲，獲得SNR為-20～20dB的接收信號。采用所提算法進行頻率估計，結果如圖8所示，橫軸表示SNR，縱軸表示100次水箱試驗平均頻率估計值。

圖8 頻率估計

可看出，隨著SNR的提高，頻率估計值逐漸趨于穩定，最終與發射頻率差值僅為0.033Hz，精度較高。試驗驗證了本文所提算法在強多途干擾水聲信道中的有效性。

5 海上試驗

2019年11月在黃海膠州灣小港碼頭附近海域進行了外場試驗，試驗地點如圖9。試驗當天多云轉陰，4-6℃，東風2級。試驗采用雙船作業形式，發射船長17.8m，寬4m，接收船長20m，寬4m，船上配有220V，3000W發電機，保障設備供電問題。

圖9 試驗地點

5.1 靜止試驗

接收船和發射船均錨定，兩船相距500m，發射船所在海域水深約9m，接收船所在海域水深約12.6m，水聽器換能器放置于水下4m，試驗參數如圖10。

圖10 試驗參數

換能器依次發射8組不同頻率的單頻信號，初始頻率7kHz，終止頻率14kHz，間隔為1kHz，每組信號連續發射兩次，每次持續時間為4s，采樣頻率為120kHz。圖11為發射頻率9kHz時水聽器接收信號，橫軸表示時間，縱軸表示幅度。應用所提算法進行頻率估計，得到八組不同頻率下的頻率估計差值(發射信號頻率值f0與接收信號頻率估計值M，2之差)，結果如圖12所示，橫軸表示發射信號頻率，縱軸表示頻率估計差值。可看出，所提算法在海上靜止試驗中仍可進行較為精確的頻率估計。但與水箱試驗相比，頻率估計差值變大，這是實際海洋中信道復雜多變以及環境等諸多因素影響所致。

圖11 接收信號(9kHz)

圖12 頻率估計差值

5.2 漂浮試驗

接收船和發射船最初相距700m，接收船錨定，發射船向遠離接收船一千多米處漂浮，其余參數同靜止試驗。儀器顯示發射船實時速度約為0.3～0.5m/s，圖13給出了兩個不同時刻點發射船速度及其與接收船的距離信息，圖13(a)顯示16時30分發射船速度為0.42m/s(0.53m/s約為1kt)，此時兩船相距1.11km(1.85km約為1nm)；圖13(b)顯示16時39分發射船速度為0.53m/s，此時兩船相距1.29km。

圖13 試驗信息

換能器依次發射8組不同頻率的單頻信號，初始頻率7kHz，終止頻率14kHz，間隔為1kHz，每組信號發射一次，持續時間為4s，采樣頻率為120kHz。圖14為發射頻率11kHz時的水聽器接收信號，橫軸表示時間，縱軸表示幅度。經計算，發射頻率為11kHz時，接收信號SNR達到25dB，因此可近似當成無噪聲處理。人為加入隨機高斯白噪聲，獲得SNR為-20～20dB的接收信號。應用所提算法進行頻率估計，得到不同SNR下的頻率估計差值，該差值即為多普勒頻移量。已知聲波在海洋中的傳輸速度c約為1500m/s，發射船運動速度的換算公式為v=c|f0-M，2|/f0。

圖14 接收信號(11kHz)

換算得到發射船在發射11kHz信號時的速度如圖15，橫軸表示SNR，縱軸表示速度估計值。

圖15 發射船速度(11kHz)

可看出，隨著SNR的提高，估計得到的發射船速度逐漸趨于穩定值0.4003m/s，與實時速度相符。

圖16為不同發射頻率下估計出的發射船速度，橫軸表示發射信號頻率，縱軸表示速度估計值。可看出，估計得到的發射船速度在0.37～0.48m/s范圍內，與試驗過程中儀器觀測到的實際速度相符，驗證了本文算法在海上漂浮試驗中的有效性。

圖16 發射船速度

6 結論

本文提出了基于牛頓迭代的水聲頻率估計算法，結構簡單，采用DFT和兩次牛頓迭代有效解決柵欄效應問題，實現水聲頻率精確估計。仿真、水箱試驗及海上試驗結果均表明，該算法在低SNR下具有良好的估計性能，能夠實現可靠的水聲頻率估計。所提算法可為水下定位與導航、水下目標勘探及運動水聲通信提供直接技術支撐。