畸變光場圖像矯正方法的設計與仿真

陳 燕，張 權

(中北大學信息與通信工程學院，山西 太原 030051)

1 引言

因拍攝環境光照影響或者工具自身限制，所獲得圖像會存在光場畸變問題，難以在亮度不均衡的圖像內提取有用數據信息，若被拍攝物體表面不平滑，致使各部分對光線的吸收和反射效果大不相同，也會產生畸變現象。

為此相關人員研究出以下解決方案：席佳祺[1]等人針對低照明度環境下圖像光場不均衡問題，通過色彩像素和對應位置信息的相互關系，構建畸變噪聲濾波算法，去除圖像內無效光照數據，最大程度保留圖像細節。但濾波器選擇不準確會給整個過程帶來干擾，矯正后圖像邊界會有模糊、不清晰情況；晏濤[2]等人提出一種基線圖像編輯法，首先需要確定對應相機參數，求出每個目標點視覺差別圖，然后運用基線編輯法對其進行重新處理，將圖像投射到與之對應的視點，最后采用深度學習算法矯正圖像。按照上述過程進行多次操作，可以修復因照度不均勻產生的畸變光場圖像，然而該方法也存在弊端，由于背景經過多次處理，過度曝光導致圖像粗糙、顏色失真，無法達到對復雜背景圖進行平滑處理的效果。

綜合上述優勢和問題，本文采用改進Hough變換方法矯正畸變光場圖像，Hough變換[3]可根據圖像內容分割全局特征、明確目標和背景之間的差異，連接具備特定形狀像素點，使主體邊緣平滑，強化目標特征信息，優化后期畸變光場矯正效果。傳統Hough變換可以幫助圖像矯正，且不依賴直線連續的特點，但提取過程中，如果有多條直線存在，往往會提取出少量不需要矯正的光場線，增加無用的計算量，降低矯正速度，在實際應用時有很大局限性。為此采用改進的Hough變換，在提取過程中截取出直線最外圍，利用直線交點坐標保證檢測出的結果是準確目標，解決了多條直線干擾、圖像失真和模糊等問題，矯正了非正視圖像，得到輪廓清晰圖像后，將畸變背景光場定義成低頻信號，選擇高斯差分(DOG)濾波器，將空域卷積運用在濾波過程中，優化選擇的參數，去除低頻畸變光場信號，得到最終矯正結果。經過詳細分析和仿真驗證，方法解決了圖像邊界模糊等問題，使畸變光場圖像矯正效果更理想。

2 改進Hough變換算法下光場畸變矯正

2.1 畸變光場圖像內非正視區域改進Hough變換

在參數空間[4]中，通過Hough變換得到極值點的取值，檢測圖像中直線、曲線，并確定線條參數，提取出規則曲線。它依據圖像的全局特征，把特定形狀像素點連接起來，使主體邊緣平滑，把源圖像點映射到累加的參數空間上，檢測出已知解析式曲線。此方式受到邊界間斷以及噪聲影響干擾比較小，變換后圖像輪廓清晰，利于優化后續矯正效果。

參數空間中每一點都可以與圖像上任意直線區間一一匹配，但是任意圖像上的像素會在多條直線區間中存在，二者并非是一一對應的。本文將圖像上的直線區間假設為一個棋盤，令特定像素假設成存在于棋盤中的棋子，但是，在這里任意棋子并非固定于某個特定棋盤內，它們可以存在于多個區域中。那么就可以理解為運用Hough變換圖像中每個棋子，也就是對特定像素[5]進行檢測，然后找到含有棋子的棋盤，也就是平面上直線區間，再在每個棋盤統計數量上+1，通過上述過程，就可以檢測出每個區間包含的特定像素數量。當某個直線區間中出現了足夠多特定像素時，就可以排除干擾，確定在這個區域中表示的直線是存在的。

如果圖像中有大量直線，直接運用Hough變換提取出的結果往往不是準確目標，因此本文在原有算法的基礎上進行了改進。提取直線過程中，在寬度>1的情況下，就需要將最外圍截取出來，然后準確記錄好每一個端點數值，最后運用Hough變換結果來計算直線交點，這時得出的數值即直線端點。避免計算結果是直線內部點或者是直線延長線、以及其它干擾提取交點情況，準確檢測出所需目標點。圖1為畸變圖像透視變換圖。

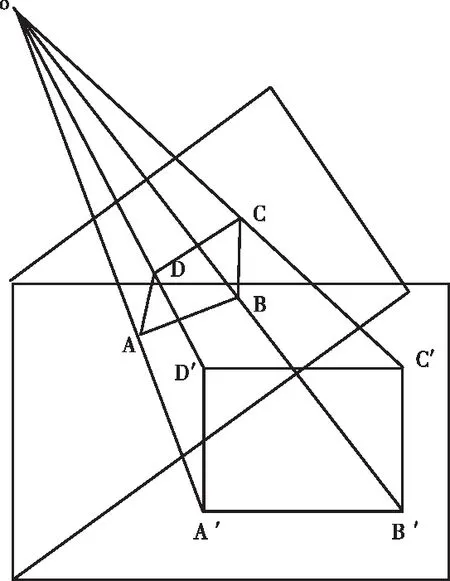
圖1 畸變圖像透視變換圖

圖1是一個畸變圖像內的非正視區域，可通過透視變化為正視平面圖像，這個過程表示為

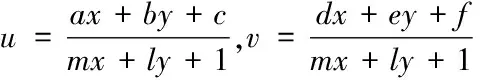
(1)

式中，(x，y)為畸變圖像的像素坐標，(u，v)為正視圖的像素坐標，a、b、c、d、e、f、m、l為變換參數。

使用算法的過程中，需要確保圖像中存在四條相交直線，運用改進的Hough變換定位出四個點坐標，把實際點坐標和定位出的點坐標當成解析上述矩陣的已知量，運用這四對數據可以解出參數向量，最后得到想要的參數值。將式(1)改寫為

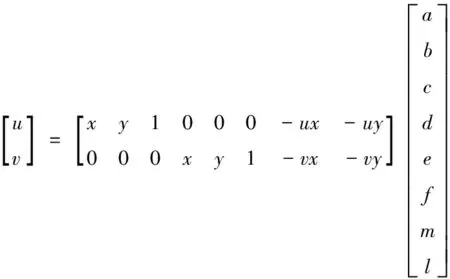
(2)

有八個相對獨立參數存在于變換式中，運用圖像點對的方式來進行二維平面變換計算。把存在于畸變圖像中每個像素點的坐標標記為：(x1，y1)、(x2，y2)、(x3，y3)、(x4，y4)；對應正視圖中點的坐標為(u1，v1)、(u2，v2)、(u3，v3)、(u4，v4)；于是可以得到

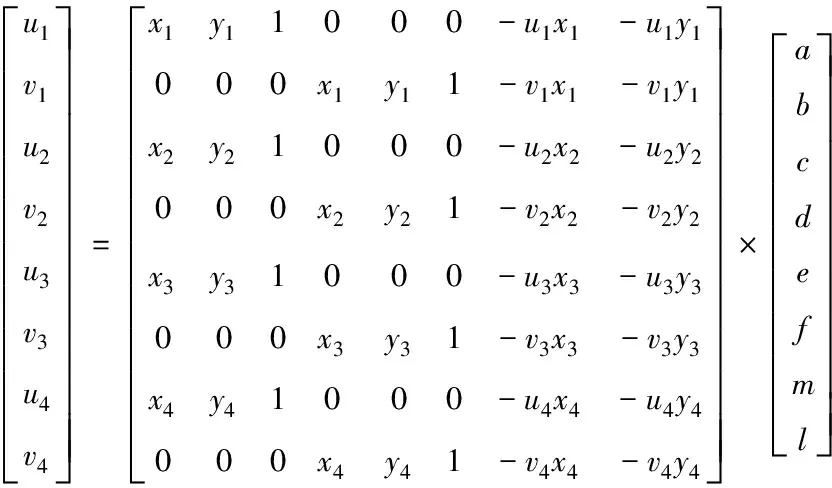
(3)

非正視區域的正視矯正結果記作

UV=A×M

(4)

其中變換參數間關系式為

M=A-1×UV

(5)

通過上述獲得對應的矯正參數值，由于畸變光場導致的非正視圖像細節丟失誤差，提取需矯正光場圖像內目標輪廓特征，幫助后續實現優質光場矯正效果，防止矯正過程中出現圖像失真或者不清晰問題。

2.2 高斯差分下畸變光場圖像矯正方法

2.2.1 光照不均矯正圖像光場分析

獲得一幅在非均勻光照[6]射線下，光場畸變圖像上某個像素坐標(x，y)，用下列公式表示出亮度值B

(6)

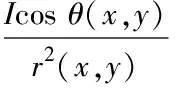
F(x，y)=R(x，y)S(x，y)

(7)

被檢測物體的表面反射效果[7]決定了R(x，y)的取值，可以最大程度描述正視變換后圖像邊緣特征，使矯正后結果清晰準確。外部光照條件決定S(x，y)取值。

通過上述分析可知，光場畸變問題是由于作用在物體上的光照不均勻現象導致的，如果能夠消除不均衡光在原來目標上的作用效果，將S(x，y)從F(x，y)中分離并去除，只留下R(x，y)，那么就可以解決光場畸變問題。因此，考慮將式(7)的兩邊以對數取值，可得到

log2F(x，y)=log2R(x，y)+log2S(x，y)

(8)

則S(x，y)和R(x，y)從原來相乘關系轉變到相加的關系，此時更利于將不均衡光照從原圖像中分離出來。

對S(x，y)、R(x，y)兩者進行分析后，可以知道，因為被檢測物體表面反射特性決定了R(x，y)的取值，其值影響物體具體細節特征，所以得出圖像頻譜[8]中與之對應的是高頻分量。而S(x，y)值由外部光照決定，變化速度非常緩慢，圖像頻譜中與之對應的應該是低頻分量。

由此可知，選擇出適合的低通濾波器[9]是圖像矯正關鍵，使畸變光場作用效果從原圖中分離出來。

2.2.2 高斯差分濾波器下矯正實現

本文選用高斯差分濾波器[10]，通過高斯差分函數有效去除圖像內的低頻分量，其傳遞函數由寬度值不相同的兩個高斯函數A1、A2進行差分得到

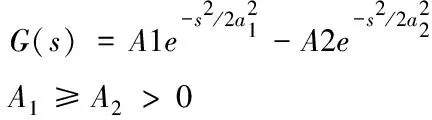
(9)

式中，寬度值a1>a2。

為了構建用于分離畸變光場的高斯差分(DOG)濾波器，首先考察傳遞函數0頻率處增益λ值，式(9)中，讓傳遞函數s=0得到

G(0)=A1-A2

(10)

如果要滿足濾波器阻帶內0≤λ<1這一條件，那么需要有

0≤A1-A2<1

(11)

讓差分結果G的最大值為Gmax，根據式(9)可以得出Gmax≤A1，再由通帶增益λ≥1，也就是Gmax≥1，可以得出

A1≥1

(12)

式(11)和(12)共同約束了A1、A2參數值，為了方便操作，令A1=A2=1，a1、a2的取值由背景頻帶寬度W0決定，因此不能得出唯一解，在計算中可以依據實際需求進行挑選。例如分離圖像內目標細節干擾，需要過濾掉高頻噪聲，這時就可以選擇合適的解來設計帶通頻譜。接下來討論a1趨于無窮大的這種情況，在此條件下，傳遞函數可以表示為

G(s)=1-e-s2/2a2

(13)

依據高斯函數3-σ規則[11]，可以得到標準差α取最優值的條件為

3αopt=W0

(14)

把上述結果運用到空域中，從式(14)的傅里葉逆變換得到DOG沖激響應為

(15)

式中，δ(x)表示單位沖激函數。

得出標準差σ的最優值為

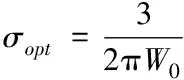
(16)

DOG卷積核的尺寸由式(16)決定。式(17)卷積積分公式可以得出運用該核對輸入信號f(x)的濾波矯正結果

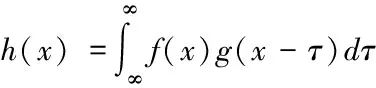
(17)

最終由式(13)、(15)得出：在頻率大于背景頻帶寬度W0的情況下，濾波器通帶增益值恒等于1，可以實現在高分量通過時，矯正后圖像不出現失真情況；在頻率小于W0時，濾波器通帶增益值小于1，依據高斯曲線遞減規律，濾波器通帶增益值下降為0，在這樣的情況下，比W0低的頻譜全都被濾波器抑制了，即去除了畸變光場。

通過δ(x)的特性可以得到

f(x)δ(x)=f(x)

(18)

聯合式(15)、(17)可以得出

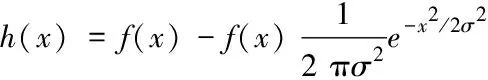
(19)

通過上式得出，高斯差分濾波器可有效將畸變光場作用效果從原圖中分離出來，矯正過程可總結為運用原來輸入的信號減去高斯核與它做卷積得到的信號。

3 仿真結果及分析

為檢測本文算法對畸變光場圖像矯正的有效性，設定仿真環境為Visual Studio2015，計算機配置為Windows7系統，數據來自任意開源數據庫。

選用不同光照環境下復雜圖片，將本文算法結果與畸變噪聲濾波法、基線圖像編輯法進行對比，從圖2、3、4、5對比中可以得出，3種方法都能夠在一定程度上實現畸變光場圖像矯正，但是圖3畸變噪聲濾波法，由于濾波器選擇不準確，給整個過程帶來干擾，導致圖像邊界模糊、不清晰情況；圖4運用基線圖像編輯法，過度曝光導致圖像粗糙、顏色失真現象；圖5運用本文提出的算法，憑借改進Hough變換在保證圖像具有清晰輪廓前提下，調節了光場作用效果，還原背景區間真實情況，相比其它方法矯正效果視感最好。

圖2 存在畸變光場的原圖

圖3 畸變噪聲濾波法矯正后效果

圖4 基線圖像編輯法矯正后效果

圖5 本文算法矯正后效果

上述照片僅體現主觀視覺效果，為了增加結果的準確、客觀性，在實驗中引入亮度均勻性評價函數、清晰度、和信息熵值[12]，從圖像光場均勻性、邊界清晰程度、細節信息完整情況這幾個角度進行驗證。

正常情況下，檢測圖像光場均勻性常常運用圖像亮度矩陣標準差，但是在散射屏中，因為系統原有結構決定了圖像中比較暗的區間，經常把總亮度曲線谷值設置成需要矯正的亮度目標。而原圖像亮度高于矯正后亮度值，運用圖像亮度矩陣標準差只能看出光場均勻性的大概情況，體現不出具體細節，所以實驗中挑選亮度均勻性評價函數當作評價指標。這個指標中Hp×q為圖像亮度矩陣，hi，j為第i行第j列的像素，光場均勻性評價標準為

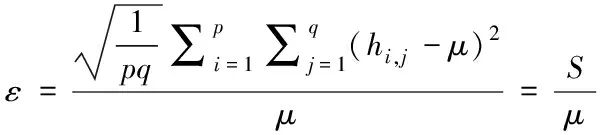
(20)

式中，ε表示亮度均勻性評價函數，h表示圖像亮度矩陣，平均值為μ，標準差為S。這個函數同時兼顧了圖像內各區域的亮度差和亮度水平，ε數值越小，說明光場越均勻。

清晰度和信息熵值計算公式如下

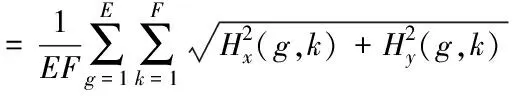
(21)

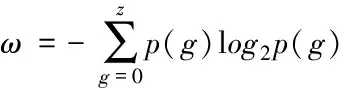
(22)

式中，?為清晰度，ω為信息熵值，g、k為像素值，p(g)為g出現在圖像中的概率，z為灰度值范圍，Hx(g，k)和Hy(g，k)為H在x，y方向上的導數，E和F為圖像尺度。?值越大圖像越清晰，ω值越大說明圖像所攜帶的信息量越多。

表1是5000幅畸變光場圖像采用上述三種方法進行矯正后，亮度均勻性、清晰度和信息熵值的平均值對比情況。

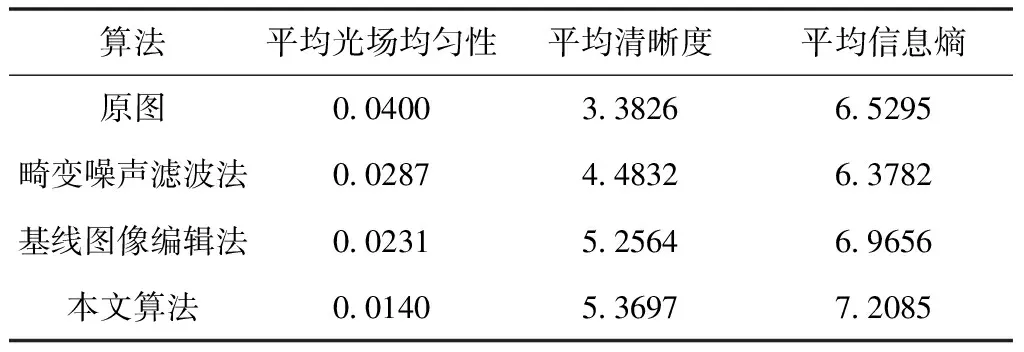
表1 不同算法畸變光場圖像矯正效果對比

從表1的對比結果中可以清晰看出：運用本文算法進行矯正后，無論是亮度均勻性、清晰度還是攜帶信息量均優于其它算法，客觀驗證了本文算法對畸變光場圖像可以進行高度還原，矯正效果較好。

4 結論

光場照度不均勻導致圖像產生畸變現象，為了對其進行有效矯正，本文在傳統Hough變換的基礎上，改進算法，保證提取目標的有效性，解決了多條直線干擾、圖像失真等問題。得到輪廓清晰圖像后，選擇適合的低通濾波器解決光場照度不均勻問題。本文選用高斯差分濾波器，將畸變光場作用效果從原圖中分離出來，保證矯正的有效性。用對比實驗，從主客觀兩個角度，對多幅畸變光場圖像矯正結果的亮度均勻性、清晰度和信息熵值平均值進行比較，結果表明本文算法可以有效解決光場圖像畸變問題。