基于改進人工勢場法的自動駕駛路徑規劃方法

馬慶祿，黃光浩

(重慶交通大學交通運輸學院，重慶400074)

1 引言

近年來，自動駕駛技術的成熟使得無人車逐漸走入大眾的視野。想要保證其安全平穩的運行，精確的路徑規劃是必要的。移動機器人的路徑規劃是其重要的分支之一，而自動駕駛車輛是移動機器人的一種實體形式，因此許多學者將移動機器人路徑規劃的方法應用于自動駕駛車輛的規劃之中。

應用較多的算法主要有基于搜索的方法：A*算法[1]、基于采樣的方法：PRM概率圖算法和RRT快速搜索隨機樹[2-3]、基于離散優化的方法：貝塞爾曲線和三次樣條插值曲線[4-5]、還有人工勢場法[6]、智能優化算法如遺傳算法[7]等。其中人工勢場法是路徑規劃研究中比較成熟和實時性較好的規劃方法，其原理簡單、計算量不大、對于未知環境的應對能力較好，規劃中實時考慮周圍障礙物的情況且便于控制。但也存在目標不可達問題和容易陷入局部極小值的情況，這會導致復雜環境下路徑規劃失敗。

針對人工勢場法可能存在的問題，眾多學者對其進行了改進。Sato提出利用拉普拉斯方程求解勢能，改進的勢場方程有效地消除了極小值點[8]。韓永等在原有的基于相對位置的勢場函數基礎上，通過構造相對速度引力勢場和相對速度斥力勢場使機器人能適應未知動態的環境[9]。Saeid Fazli等人采用“沿墻走”方法來解決障礙物附近目標不可達問題以及復雜環境下路徑規劃問題[10]。李東方等通過調整引力增益系數、斥力增益系數、障礙物的影響范圍以及機器人的運動頻率等參數以獲得最優路徑[11]。任彥等提出當機器人陷入局部極小值時對機器人施加附加虛擬控制力以跳出局部極小點[12]。石為人等提出通過建立基于聲吶傳感器的機器人模型，分別計算不同方向所受的斥力大小，當機器人遇到極小值點時將該區域障礙物連接為整體快速遠離該區域[13]。羅乾又等提出設置虛擬目標點的方法，對機器人所受合力為0時通過實際目標點與虛擬目標點的共同作用下擺脫局部極小值[14]。修彩靖等在考慮道路邊界的引力約束以及車輛約束后，利用高斯組合隸屬函數來優化引力函數，證明勢場法適用于在結構化環境下運行的無人車[15]。程志等通過引入機器人實時前進向量來跳出局部極小值點，引入虛擬目標點以逃離障礙物陷阱[16]。溫素芳等對于目標點周圍存在障礙物提出縮小其影響范圍來減小斥力抵達目標點，將障礙物的影響范圍分層討論以逃離局部極小值點[17]。翟紅生等利用量子粒子群算法優化勢場函數中的增益系數，有效解決了復雜動態環境下隨機障礙物的避障問題[18]。梁獻霞等通過扇區劃分的方法構造虛擬障礙物，使得局部極小值點的機器人在虛擬障礙物和目標點以及真實障礙物三者力的作用下擺脫該區域[19]。魏立新等通過將模糊控制算法和改進的人工勢場法結合，解決了U型陷阱和動態障礙物問題[20]。羅強等提出了做機器人對于障礙物勢場范圍的切線來確定虛擬的逃逸力，通過搜索法來判斷障礙物之間的可行區域來逃離極小值點[21]。王洪斌等將改進的二次A*搜索算法與人工勢場法相結合，實現了機器人動態規劃路徑的長度與平穩度較優[22]。

本文介紹了傳統人工勢場法原理，分析在傳統人工勢場法進行路徑規劃時出現目標不可達和局部極小點情況的問題。在改進的引力勢場函數上通過設定距離閾值來避免引力過大的導致不能避障問題，在改進的斥力勢場函數上，通過引入斥力調節因子并將車輛與障礙物的距離分段討論，使得自動駕駛車輛能夠順利逃離局部極小點抵達目標。

2 傳統人工勢場法原理

Khatib[6]于1986年提出人工勢場法，基本原理是將自動駕駛車輛運行區域設置為由一個引力勢場和若干個斥力勢場組成的虛擬的力場環境。預抵達的目標點周圍的引力勢場對車輛產生吸引力從而“拉動”車輛駛向目標點，吸引力的大小與車輛至目標點的距離成正比，即距離越遠吸引力越大距離越近吸引力逐漸減小。行駛過程中遇到的人、其車輛等障礙物會對車輛產生排斥力從而“推動”車輛遠離障礙物達到避障的效果，排斥力的大小與車輛至障礙物的距離成反比，即距離越遠排斥力越小距離越近排斥力逐漸增大。自動駕駛車輛在目標點與障礙物所產生引力場與斥力場的合力場下能夠有效地避開障礙物抵達目標位置。自動駕駛車輛行駛過程中的受力示意圖如圖1所示。

圖1 自動駕駛車輛在勢場中的受力示意圖

2.1 引力場與斥力場函數

(1)

(2)

式中，S為自動駕駛車輛現在的位置(x，y)，Starget為預設目標點的位置(xt，yt)，λatt為引力勢場的常數。λrep為斥力勢場常數，Sbarrier為區域內障礙物位置(xb，yb)，障礙物對自動駕駛車輛影響的最大距離為d0。對引力勢場函數和斥力勢場函數分別求解負梯度，即引力與斥力對距離求導可得引力場函數和斥力場函數公式見式(3)和(4)

Fatt(S)=-?Uatt(S)=-λatt|S-Starg et|

(3)

Frep(S)

(4)

2.2 合力場函數

自動駕駛車輛在接近目標點的過程中，目標點只有一個但障礙物不止一個，若存在n個障礙物則車輛會受到n個斥力勢場疊加起來的作用。可見引力只有單個目標點產生，斥力則會由n個障礙物產生。整個行駛區域內的總勢能為引力勢能與斥力勢能之和，車輛受到的合力為所受的引力和斥力之和，根據上述公式可求得總勢能函數與車輛所受合力為

(5)

2.3 人工勢場法存在的問題

1)目標不可達問題。當距目標點很近的范圍內存在障礙物時，此時由式(4)可知障礙物的斥力隨著距離的減小而變得很大，由式(3)可得目標點的引力隨距離的減小變得很小，這就會造成自動駕駛車輛受到的勢場合力一直指向目標方向的反方向，從而使得車輛停滯無法前進到達指定的目標點。

2)局部極小值問題。引力與斥力的合力決定自動駕駛車輛的移動方向，當車輛在某一點所受到的合力為零或者合力方向與引力和斥力共線時，車輛將無法確定下一步的前進方向，可能會出現停止或者徘徊的情況。下圖2中展示了兩種導致局部極小值問題的障礙物分布類型，分別是“U”型障礙物、“L”型障礙物與目標點共線的情況。

圖2 自動駕駛車輛在勢場中陷入局部最小值的幾種情況

3 改進的勢場法

3.1 引力場函數的改進

由式(3)可知目標點的引力是和車輛與目標點的距離成正比，也就是說當二者距離較遠時，此時引力相當大，周圍障礙物的斥力相比引力而言會較小，這可能導致車輛受到很強的引力來不及躲避障礙物與其相撞。對于引力過大的問題，對引力場和引力函數進行改進，公式為

(6)

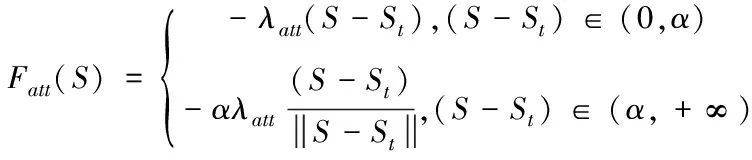
(7)

式中α為人為設定的距離閾值，也可以理解為目標點對車輛的影響距離。當車輛位置與目標點位置距離大于設定的距離閾值α時，引力則為常數。當車輛位置與目標點位置距離小于設定的距離閾值α時，可認為車輛行駛到目標點影響距離以內，此時引力同未改進前一樣與二者距離成正比。

3.2 斥力場函數的改進

對于目標不可達問題和局部極小值問題，需要對傳統人工勢場法中的斥力勢場函數進行改進，保證車輛在遇到上述幾種局部極小值的情況下能夠抵達并穩定在目標點，即整個勢場中目標點是全局最小值。常用的方法是將車輛與目標點的相對距離的n次方引入到原有的斥力勢場函數中，即(S-Starget)n為斥力函數調節因子。對于障礙物的影響距離進行分段，在不同的距離閾值采用不同的斥力，使得目標點位置的斥力為零，車輛穩定于目標點。

斥力增益系數λrep為正數，障礙物對車輛的影響距離d0，車輛與障礙物距離大于d0時不受此障礙物的影響，這里在S0與障礙物邊界之間增加一個距離閾值d0/2。

當S-Sbarrier∈(d0，+∞)時，車輛處于安全區域不會與障礙物碰撞此時斥力勢場和斥力都為0，S-Sbarrier∈(d0/2，d0)時，車輛處于控制區域此時障礙物產生斥力作用于車輛且線性收斂，S-Sbarrier∈(0，d0/2)時，車輛處于危險區域，當車輛進入即將發生碰撞的危險區，所受的斥力要保證其盡快遠離該區域。

(8)

對斥力勢場求負梯度，由式(8)計算得到斥力，其公式為

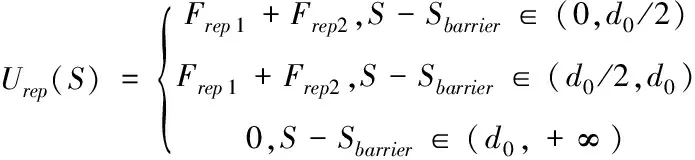
(9)

(10)

式中n可以取大于0的任意常數，Frep的兩個分力為Frep1和Frep2，二者都是是障礙物對車輛的斥力分力，Frep1受力方向從障礙物指向車輛，Frep2受力方向從車輛指向目標點。斥力函數調節因子(S-Starget)n中n的取值影響到自動駕駛車輛的受力情況，故對其進行討論以分析不同取值下Frep1和Frep2的大小。

1)n∈(0，1]

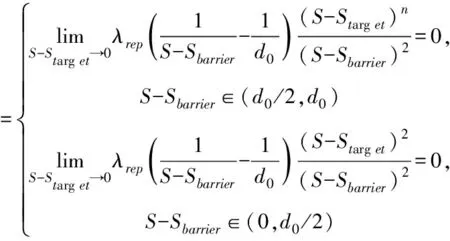
(11)

(12)

當自動駕駛車輛靠近目標位置時，無論是S-Sbarrier∈(d0/2，d0)的控制區還是S-Sbarrier∈(0，d0/2)的危險區，此時障礙物對車輛的斥力Frep1都趨于0。目標點對車輛的引力Frep2在S-Sbarrier∈(d0/2，d0)的控制區內趨于無窮大，在S-Sbarrier∈(0，d0/2)的危險區內趨于0。當n在(0，1]內，車輛處于控制區時在Frep2和Fatt的共同作用下靠近目標位置，處于危險區時只在Fatt作用下靠近目標位置。

2)n∈(1，+∞]

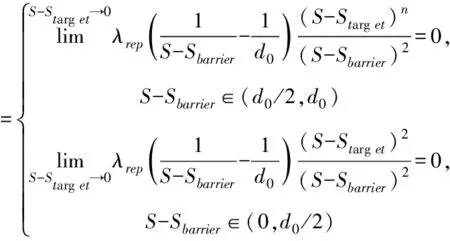
(13)

(14)

當自動駕駛車輛靠近目標位置時，無論是S-Sbarrier∈(d0/2，d0)的控制區還是S-Sbarrier∈(0，d0/2)的危險區，此時障礙物對車輛的斥力Frep1、Frep2都趨于0。此時車輛只在Fatt作用下靠近目標位置。

4 Matlab仿真分析

本文選取重慶交通大學南岸校區內障礙物環境為研究區域，起點為重慶交通大學1號門，目標點為菁園小區，黑色方框內為路徑規劃區域，將區域內建筑物障礙物全部抽象為圓形障礙物，計算勢場力，試圖規劃出一條無碰撞的自動駕駛車輛路徑，研究區域如圖3。

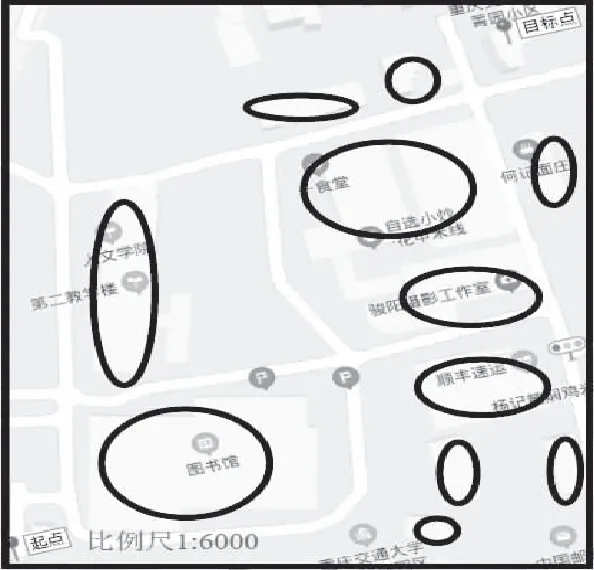
圖3 重慶交通大學南岸校區1號門-菁園小區

利用 Matlab 2016a軟件針對傳統的人工勢場法的存在的問題進行仿真，以下仿真結果是在障礙物均為靜態的前提下進行的，步驟如下：

1)仿真環境設置為x軸為8、y軸為9的二維區域，起始位置設為(0，0)，目標位置為(7.2，8)。引力勢場增益常數λatt=1000斥力勢場增益常數λrep=15。自動駕駛車輛的步長l=0.1，障礙物的影響距離p0=1。

2)計算的車輛和各個建筑物障礙，和目標點之間的與X軸之間的夾角(統一規定角度為逆時針方向)

3)根據車輛當前位置與目標和障礙物的角度，分別計算引力和斥力在x和y軸方向的分力。

4)根據引力與斥力在x軸方向的分力的合力，在y軸方向的分力的合力，確定車輛下一步的x坐標和y坐標，更新位置坐標、與障礙物和目標點的角度，記錄車輛走過的點。

5)判斷是否車輛達到目標點，若抵達則步驟結束，否則將重新轉入步驟3)。

傳統勢場法下路徑規劃在不遇到復雜障礙物的前提下可以順利達到目標點，本文實驗則遇到了局部極小值致車輛無法抵達目標點的情況，見圖4(a)，對勢場函數進行改進后見圖4(b)。

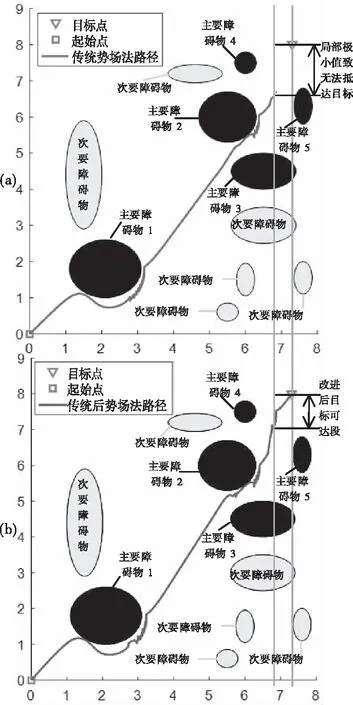
圖4 傳統勢場法與改進勢場法下自動駕駛車輛路徑規劃圖

圖4中黑色實心圓代表影響路徑規劃的主要障礙物，淡藍色實心圓代表對路徑規劃無影響的次要障礙物。紅色方形代表起始點，藍色三角形代表目標點，紅色實線代表傳統勢場下車輛的運動軌跡，藍色實線代表改進后車輛的運動軌跡，傳統人工勢場法下，自動駕駛車輛沒有成功繞開障礙物，陷入了局部極小值最終沒能抵達目標點處。改進的人工勢場下，車輛成功繞過障礙物避免了陷入局部極小值到達目標點位置。

對傳統勢場函數與改進后勢場函數分別求路徑過程中總勢場值見圖5。

圖5 傳統勢場法與改進勢場法勢場曲線圖

圖5為與兩種方法所對應的勢場曲線圖，圖5(a)對應傳統勢場法，可以看到，當車輛運行到第81步的時候，總勢場陷入了局部極小值，因此車輛在此處停滯不前；圖6(b)對應改進人工勢場法，可以看到運行到第141步時，雖出現了局部震蕩但總勢場沒有出現局部極小點，因此最終可以到達目標點。

自動駕駛車輛路徑規劃目的是為了規劃出安全無碰撞且相對平滑的路徑，因此這里引入路徑規劃的評價模型對傳統勢場法與改進后勢場法所規劃出的路徑進行量化評價[23]。

(15)

式中，V為評價值，V越大，表明規劃路徑的質量越高；W1、W2、W3為權重系數，且三者和為1；C、T、L、X分別為碰撞系數、轉點數量、直線行駛長度以及尋路時間，這些參數的含義如下。

對于車輛規劃而言，基本的要求就是不與障礙物發生碰撞，因此規定C=1為無碰撞，C=0時視為撞到障礙物路徑規劃失敗。路徑平滑度通常需要參考轉折點數，轉點數量越多說明路徑規劃的平滑度越差，反之則平滑度越好。路徑的長度可以確保的情況下，直線行駛長度越長，則說明規劃出的路徑無需車輛保持較高的靈敏性，反之則要求車輛保持較好的轉向性。路徑規劃時間的大小可以一定程度反映資源的消耗，路徑時間越短規劃的結果一般越優。

應用規劃路徑評價模型來評價傳統勢場法與改進后勢場法規劃出的路徑，結果見表1。

表1 兩種勢場法評價對比

由表1，可以明顯的看出傳統與改進后兩條規劃的路徑都是無碰撞的，改進后直線行駛長度L明顯變長，說明規劃路徑中更多是直線規劃，降低了對車輛自身機動性的要求，轉折點數量進一步減小說明路徑的平滑度提升，尋路時間相較于傳統勢場法較長是由于改進后的路徑抵達了目標點。最終路徑評價值V 顯示，改進勢場函數的路徑較傳統勢場在評價值方面提高了64%，說明基于勢場函數的改進模型大大提高了路徑規劃的質量。

5 結論

針對傳統人工勢場法中當車輛距離目標點較遠時引力過大斥力過小而無法避開障礙物的情況下，通過引入車輛與目標位置之間的距離閾值α，大于閾值α時引力為常數，小于閾值α時引力與距離成正比以解決避障問題。對于傳統勢場法中的目標不可達和局部極小值問題，本文對于斥力函數進行了改進，在改進的斥力函數中加入斥力調節因子，并對障礙物的影響范圍分進行段討論，通過設定障礙物分段影響距離點計算不同的斥力。最后以重慶交通大學南岸校區1號門為起點菁園小區為目標點，所在區域進行實地路徑規劃，利用Matlab2016a對自動駕駛車輛仿真的結果表明改進后的勢場法有效，畫出了車輛規劃的路徑，并對傳統勢場法與改進后勢場法進行量化評價，結果表明改進后勢場函數在評價值上提高了64%，明顯提高了路徑規劃的質量。