油田剩余可采儲量預測算法設計及性能測試

郭 瑾，矯欣雨，孫 肖

(1. 山東石油化工學院油氣工程學院，山東 東營 257061；2. 中國石油大學(北京)石油工程學院，北京 102249)

1 引言

油田剩余可采儲量預測是油田開發的基礎，同時也是評價油田開發效果的重要指標[1，2]，具體的預測方法主要包括經驗公式法和遞減法等。但是大部分方法都比較適用于新開發的油田區，計算結果和真實結果存在一定的差異，經過較長時間的開發調整之后，各項指標逐漸趨于穩定，會獲取固定的變化規律，但是老區的可采儲量無法直接在當年展示出來，滯后性較強。

為了有效解決上述問題，相關專家針對油田剩余可采儲量預測方面的內容進行了大量研究，例如孫科等人[3]針對油藏工程基本理論提出一種了全新的可采儲量預測方法，分析采出程度和含水率之間的關聯，同時采用兩者之間的關系版圖完成預測。賈林等人[4]優先通過地質儲量和甲型水驅規律曲線斜率之間的關系，計算童式圖斑系數的取值；然后根據改進的甲型水驅規律曲線，得到無水采收率和水驅規律曲線的積分常量，同時繪制改進的童式版圖，最終將其應用于采收率的預測中。

在上述兩種方法的基礎上，本文提出了一種基于蒙特卡洛法的油田剩余可采儲量預測算法，經實驗測試證明，所提算法能夠快速準確完成油田剩余可采儲量預測。

2 油田剩余可采儲量預測算法

2.1 油藏數據預處理

將信息熵應用到油藏數據預處理中，同時引入加權歐式距離理論來全面提升油藏數據聚類效果的準確性[5，6]。

1)設定一個樣本集X，其由n個m維樣本數據構成，對應矩陣的表達形式如下：

(1)

2)為了獲取更加精準的聚類結果，需要對全部數據進行歸一化處理。

3)計算數據集X中第i個樣本對應第j列屬性所占的比重Pij，具體的公式為

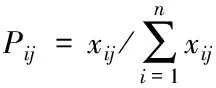
(2)

4)計算屬性j對應的信息熵Ej，如式(3)所示

(3)

5)采用式(4)計算屬性j的差異系數qj，即

qj=1-Ej

(4)

6)采用式(5)計算屬性j的權重ωj，即：

(5)

當經過計算獲取屬性的權重后，給出數據對象a和b的加權歐式距離dist(xa，xb)，具體的計算公式為

(6)

式中，xaj和xbj分別代表研究對象a和b對應的第j列屬性值。

在油藏數據預處理中，需要進行異常檢測的數據集通常包含正常和異常兩種數據[7，8]，選取一個初始中心，其應滿足密度高于數據集平均密度，初始聚類中心選擇算法詳細的操作步驟如下所示

1)設定樣本集X={x1，x2，…，xn}，最近鄰數據共包含t個點數，聚類中心數量為K，計算X中數據點xj的密度，具體的計算公式為

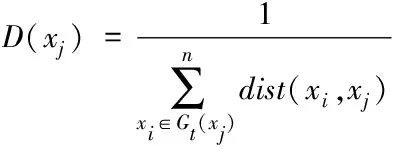
(7)

式中，Gt(xj)代表的是第t個最近鄰數據點集合。

2)計算全部數據對象的平均密度D，通過D(xj)>D的數據點形成全新的數據集X′。

3)計算X′中各個樣本和前i-1個初始聚類中心加權歐式距離的最小值，將其放入到對應的集合中，直至滿足設定的約束條件。

設定數據集中各個數據對象的初始異常度為Fj，通過信息熵計算屬性權重的方式獲取數據集對應的屬性權重。通過初始聚類中心選擇方法確定初始聚類中心的數量，同時計算數據對象xj到不同簇中心的加權歐式距離，同時將xj劃入到聚類中心所在的簇中。結合相關約束條件，重新形成各個簇的中心點。假設數據對象xj的異常度Fj≥η，則說明該油藏數據點為異常數據點，同時將其加入到異常點集合中，最終實現油藏數據預處理。

2.2 基于蒙特卡洛法的油田剩余可采儲量預測模型

油田剩余可采儲量預測是油田勘探和開發的重點內容，對油田的產量具有十分明顯的影響，需要對不同影響因素進行非線性分析，本文根據油藏數據的特性，采用蒙特卡洛法估算油田剩余可采儲量。蒙特卡洛法主要被應用在復雜且高維概率分布的試驗函數評估中，主要是通過動態模擬實現估算，同時結合新的油井生產指標和油井的生產性能構建油田剩余可采儲量預測模型。

在采用蒙特卡洛法進行模擬的過程中，除了需要考慮不同概率的相關性之外，同時還需要深入分析各個變量間的相關性。在模擬過程中，蒙特卡洛法估算油田剩余可采儲量主要借助容積公式法，如式(8)和式(9)所示

(8)

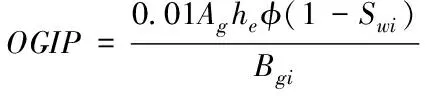
(9)

式中，OOIP和OGIP分別代表原始油田的質量和天然氣地質儲量；Ag和A0代表油田的含油比例；he代表油田的平均厚度；φ代表地表孔隙密度；Swi代表任意常數；Boi和Bgi代表油田的體積系數。

結合上述計算公式，采用蒙特卡洛法構建油田剩余可采儲量預測模型，具體的操作步驟如下所示：

1)將全部對估算結果產生影響的因素進行排隊，選取核心要素納入到系統中。

2)確定目標函數。

3)通過任意一組隨機變量獲取對應的參數取值。

4)將隨機一組參數代入到式(8)和式(9)中，求解目標函數值。

5)引入油田生產指標和生產性能，以此為基礎建立油田剩余可采儲量預測模型。

2.3 油田剩余可采儲量預測模型優化

為了提升預測模型的性能，采用粒子群算法對預測模型進行進一步優化。粒子群算法主要是受到鳥群覓食行為的啟發提出的一種優化算法。設定鳥群在隨機尋找食物，整個區域內只含有一個食物，而鳥群的位置是不固定的[9，10]。設定目標搜索空間是D維的，在迭代過程中各個重新計算鳥群的位置和速度，具體的計算公式為

(10)

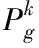
慣性因子的計算公式為

(11)

式中，wmax和wmin分別代表最大和最小慣性因子取值。

為了更好地實現尋優，需要在尋優的過程中不斷對慣性因子wi進行調整，直至獲取最佳適應度取值，則停止尋優[11，12]，具體的計算公式如下

wi=wmax-(wmax-wmin)*f(a，b)

(12)

式中，f(a，b)代表粒子經過當前迭代獲取的適應度變化趨勢。

在粒子群優化算法中，需要在整個求解空間中獲取全局最優解。以下在迭代過程中加入加速因子實時調整迭代次數，具體的計算公式為

(13)

粒子群算法將目標函數設定適應值尋找全局最優解，能夠全面提升預測結果的適應性和穩定性，同時該算法還具有較好的全局搜索能力。其中，粒子群的適應度計算過程如式(14)所示

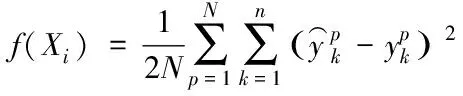
(14)

利用圖1給出粒子群算法優化油田剩余可采儲量預測模型的詳細流程：

1)確定網絡的拓撲結構，同時還需要確定不同的參數取值。

2)設定種群的規模，同時更新各個粒子的位置和速度。

3)分別計算不同粒子的適應度取值。

4)更新各個粒子的慣性因子，進而實現粒子的位置和速度更新。

5)假設滿足迭代條件，則結束迭代；反之，則返回步驟3)，重新執行以上步驟。

6)將通過粒子群算法獲取的全局最優解設定為網絡中的取值和閾值，對預測模型進行訓練，直至滿足設定的誤差需求為止。

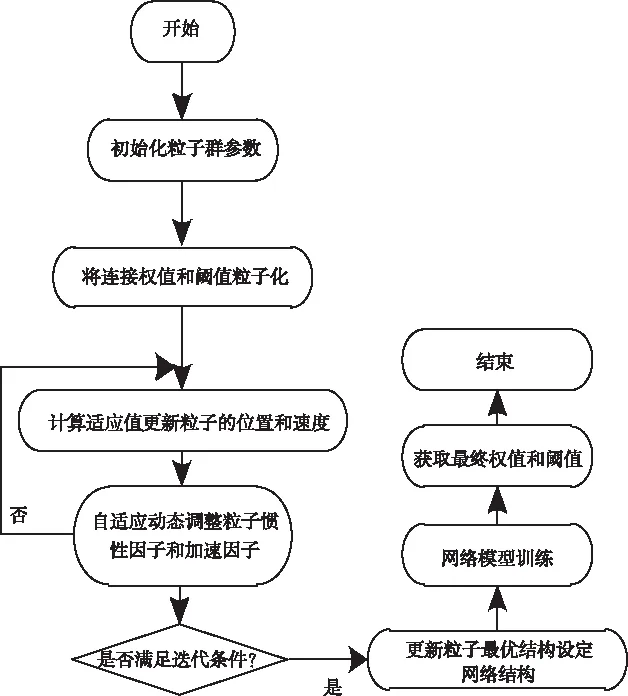
圖1 PSO優化流程圖

在上述分析的基礎上，實現粒子群算法的并行化處理，詳細的操作步驟如下所示：

1)將數據集和種群進行初始化處理。

2)分別對不同的種群進行劃分，即將數據和種群劃分為M份。

3)計算各個粒子的適應度取值，獲取自身最優值。

4)將各個節點進行通信，進而獲取全局最優的適應值。

在上述分析的基礎上，結合粒子群算法，實現對基于蒙特卡洛法的油田剩余可采儲量預測模型優化，通過優化后的模型實現預測。

3 仿真研究

為了驗證所提基于蒙特卡洛法的油田剩余可采儲量預測算法的有效性，實驗選取H城市油田開發區作為研究對象，選取200畝典型的油田構建樣本空間，其中訓練樣本和測試樣本各占一半。選取文獻[3]和文獻[4]作為對比算法，進行對比驗證。

1)時間/s

利用圖2給出三種不同算法的時間復雜度對比結果：

圖2 不同算法的預測時間對比結果

從圖2能夠看出，各個算法的預測時間會隨著測試樣本的增加而增加。但是和另外兩種算法相比，所提算法的預測時間明顯更低一些，說明所提算法能夠在較短的時間內實現對油田剩余可采儲量的預測，預測效率較高，充分證實了所提算法的優越性。

2)預測結果分析

將油田剩余可采儲量預測指標之一的油藏飽和度作為測試對象，三種不同算法的具體實驗對比結果如圖3所示。

圖3 不同算法的油藏飽和度預測結果對比

從圖3中能夠看出，所提算法的油藏飽和度和真實值更加接近，而文獻[3]算法與文獻[4]算法與真實值之間的差距較大。產生這種差距的主要原因為：所提算法對油藏數據進行了預處理，及時發現異常，有效提升了預測結果的準確性。

為了進一步驗證所提方法的預測性能，以下實驗測試油田剩余可采儲量，分別采用三種不同的算法進行預測，具體的實驗結果如圖4所示。

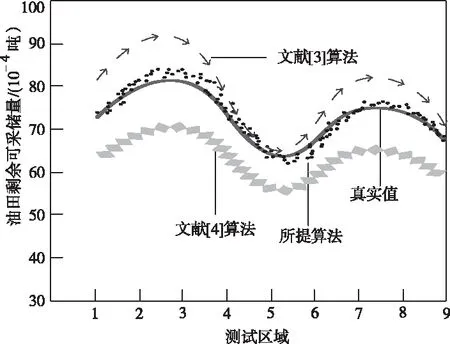
圖4 不同算法的油田剩余可采儲量對比結果

從圖4能夠看出，所提方法能夠獲取更加精準的預測結果，其預測得到的油田剩余可采儲量與真實值之間的差距較小，而傳統文獻[3]算法與文獻[4]算法與真實值之間的差距較大，充分驗證了所提算法的優越性和有效性。

以下實驗測試將均方根誤差設定為測試指標，分析各個預測算法的預測性能，其中均方根誤差取值越低，則說明預測效果越好，利用表1給出詳細的實驗對比結果：

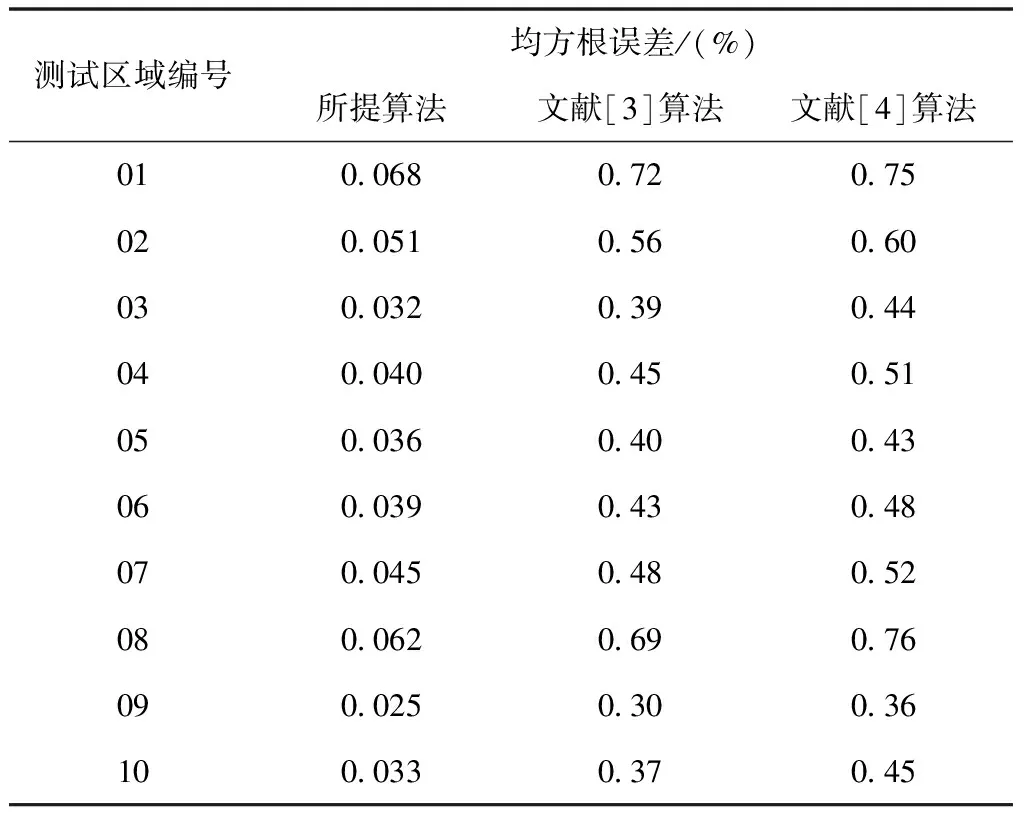
表1 不同算法的均方根誤差對比結果

從表1能夠看出，相比文獻[3]算法和文獻[4]算法，所提算法的均方根誤差取值明顯更低，且與傳統算法之間的差距較為明顯，進一步驗證了所提算法預測結果的準確性，說明所提算法的預測結果具有可靠性。

4 結束語

針對傳統算法存在的不足，結合蒙特卡洛法，提出一種全新的油田剩余可采儲量預測算法。經實驗測試證明，所提算法能夠精準預測油田剩余可采儲量，同時還能夠有效降低預測時間，通過實驗結果充分驗證了所提算法的有效性與應用價值。所提算法現階段仍然處于初步研究階段，還需要進一步研究，例如提升自身的泛化能力以及增強模型的多樣性等，接下來將以上述內容為重點，進一步提升所提算法的應用效果。