跨越線路絕緣子串脫冰動張力特性仿真分析

楊曉輝，張 博，宋 陽，胡 鑫

(1. 國網河南省電力公司電力科學研究院，河南 鄭州 450052；2. 華北電力大學機械工程系，河北 保定 071003)

1 引言

我國架空輸電線路由于冰害所導致的線路故障次數呈現上升趨勢。架空線脫冰跳躍產生的動態張力會對輸電線路各個部件造成持續不斷的沖擊[1]。當沖擊張力過大或在疲勞的作用下，導線、絕緣子串、桿塔將會產生裂紋直至發生破壞。目前對架空線路覆冰載荷問題的研究已經較為充分[2-5]，而國內外對于架空線脫冰跳躍問題的研究還在逐步進行中。A.Jamaleddine[6]等人在一條縮比的模擬兩檔線路上，通過重物載荷掉落來模擬脫冰。測得導線的最大舞動高度、各掛點的張力變化及懸垂絕緣子串的位移和偏轉角度等，并使用ADINA軟件進行了仿真。王璋奇[7-9]等通過實驗對比分析真實覆冰與集中質量覆冰情況下架空線脫冰動態響應，結果表明集中質量法可以滿足實驗要求。由于人工覆冰需要合適的氣象條件，而縮比實驗模型并不能完全反映實際情況下的導線脫冰情況，故對于架空線脫冰跳躍問題更多的還是采用計算機仿真的方法。M.Roshan Fekr[10]等采用減小單元的方法模擬導線的突然脫冰，討論了覆冰厚度、檔距長度、每檔導線數等21個參數對脫冰跳躍的影響。目前，跨越線路的研究方向主要集中于電磁場分析、跨越安全距離[11]和故障電流研究[12]等三部分，對重要跨越線路典型絕緣子串動張力特性研究較少。王笑瑜[13]等通過有限元方法分析了關鍵金具的靜態受力特性。

國內外對于輸電線路脫冰跳躍的研究，大多數只研究孤立檔，或鄰檔導線動張力的影響。而在實際脫冰情況下，脫冰動張力受到輸電鐵塔—絕緣子串—導線三者互相影響。因此，本文以某220kV“耐-直-耐”結構重要跨越線路實際工程為背景，通過分段建模的方式建立跨越線路塔線系統有限元模型，采用ANSYS單元“生死”法模擬架空導線的脫冰過程；著重分析絕緣子串動態變化規律，通過分析計算找到絕緣子串金具易損位置。

2 “耐-直-耐”跨越線路有限元模型

2.1 有限元分析理論基礎

應用三維彈性理論經推導后可以得出單元剛度矩陣和節點等效載荷表達式，結合跨越線路運動動力學方程，為重要跨越線路的有限元分析奠定了理論基礎。

利用Lagrange插值多項式，有

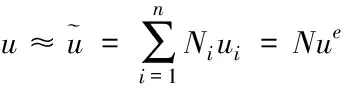
(1)

導線單元勢能方程

(2)

根據變分原理

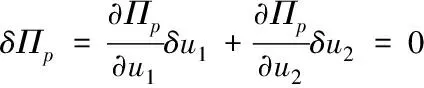
(3)

等效方程

(4)

可得導線單元剛度矩陣

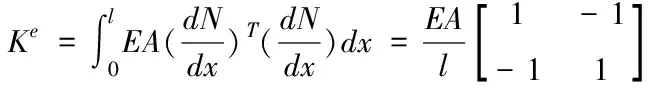
(5)

節點等效載荷

(6)

跨越線路運動動力學方程

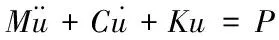
(7)

式中，u為變形位移；N為位移函數；E為彈性模量；A為截面積；M為質量矩陣；C為阻尼矩陣；P為系統外載荷。

2.2 建立跨越線路有限元模型

本文以某實際220kV跨越線路為工程背景，建立塔線系統有限元分析模型。如圖1所示，線路結構由耐張干字型塔A(呼高30m)、直線酒杯型塔B(呼高36m)、耐張塔干字型C(呼高21m)構成；跨越檔位于耐張塔A和直線塔B之間，檔距180m；直線塔B與耐張塔C之間為其鄰檔，檔距350m。輸電塔主材、橫隔材采用BEAM188梁單元模擬，絕緣子串、輸電塔斜材用LINK8桿單元模擬，考慮到導地線為柔索結構，選用LINK10索單元進行模擬。角鋼材料選用Q345號鋼材。

圖1 220kV“耐-直-耐”跨越線路結構

2.2.1 建立絕緣子串有限元模型

220kV跨越線路導線懸垂串長l=2966mm，其中復合絕緣子長l2=2461mm，其余金具部分總長為l1=505mm。使用solid186單元模擬實體單元。圖2為建立好的220kV“耐-直-耐”跨越線路右相導線懸垂絕緣子串有限元模型。

圖2 220kV跨越線路中懸垂串有限元模型

2.3 有限元仿真分析流程

2.3.1 仿真對象的選取

考慮到跨越線路往往會在直線塔的導線懸垂串處發生掉串事故。由于跨越線路跨越檔內有三相導線，故以正常運行工況為例，對塔線系統有限元計算模型施加脈動風荷載，分別提取正常運行工況下穩定后50秒內各相導線對懸垂串動張力并將最大值匯總于表1中。

表1 正常運行工況下懸垂串動張力最大值

從表1中可以看到，因三相導線懸垂串掛點位置不同，右相懸垂串與左相懸垂串動張力最大值比較接近，并且均大于中相懸垂串動張力最大值。綜合考慮，選擇跨越檔右相導線絕緣子串為研究對象。

2.3.2 絕緣子串動態響應分析流程

本文通過在導線節點上均勻施加Mass21質量單元的方式模擬覆冰；利用ANSYS單元“生死”技術，通過“殺死”施加在導線節點上的集中質量單元的方式來模擬脫冰，其實現方式是讓被“殺死”的單元的剛度乘以一個很小的縮減系數；最后采用ANSYS瞬態動力學分析方法計算導線脫冰后絕緣子串的動態響應。分析流程圖如圖3。

圖3 絕緣子串動態響應分析流程

ANSYS瞬態動力分析有多種方法，其中完全法瞬態動力分析方法采用完整的系統矩陣計算瞬態動力響應，計算功能最強。完全法瞬態動力分析方法具有如下特點：使用方法簡單，不用關心主自由度和振型的選取問題；可考慮各種類型的非線性特性(如塑性、大變形、大應變等)；通過一次計算就能獲取全部的位移和應力；可施加所有類型的載荷：節點力、外加的(非零)位移和單元載荷。因此，本文采用完全法的瞬態動力分析方法計算導線脫冰后絕緣子串動態響應。算法計算步驟如下：

1)定義完全法瞬態分析，設置適用于單元相關的質量矩陣公式，打開大變形，預應力效應，定義阻尼系數、施加重力加速度；

2)關閉瞬態分析，定義時間，階躍荷載，求解；

3)打開瞬態分析，定義輸出控制，定義時間，選擇求解子步數，求解；

4)殺死相應單元，設置求解時間進行求解。

2.3.3 塔線系統分段分析法

本文根據以上介紹的絕緣子串動態響應分析流程，通過塔線系統分段分析法研究絕緣子串的動態受力特性，即首先建立覆冰工況下的塔線系統有限元模型，脫冰計算后提取模型中跨越檔右相導線對絕緣子串的動態作用力并加載到單獨建立的懸垂串實體有限元模型上進行分析。該方法相比于全實體單元建模分析更加方便，計算容易收斂，并且提高了運算速度，保證了較高的精確度。

2.3.4 有限元模型試驗驗證算例

文獻[1，14]曾建立了檔距為130m的孤立檔導線試驗系統，在導線上等間距地懸掛重物模擬導線覆冰，導線脫冰通過控制重物掉落的方式進行模擬，并測量導線脫冰后端部的動態張力。試驗導線型號ACCC240/35，外徑21.69mm，截面積287.06mm2，單位長度質量742kg/km。將整檔覆冰脫落為5 mm的工況進行對比，并建立相對應的有限元模型。

圖4為導線端部張力時程曲線。數值模擬得到的導線端部張力和試驗測量結果基本吻合，驗證了導線脫冰數值模擬方法的合理性。

圖4 導線端部張力時程曲線

3 仿真結果與分析

考慮到目前絕緣子串脫冰情況下受力的動態變化規律研究較少，極端惡劣情況(如脫冰，舞動等)下絕緣子串異常受力容易引起金具破損。在實際脫冰工況中，往往不是全檔同時脫冰，而是檔內不同位置全部或部分脫冰，每次導線覆冰量也不盡相同。故有限元模擬分別考慮不同脫冰位置，不同脫冰量，不同覆冰厚度對絕緣子串動張力的影響。

3.1 不同脫冰條件下絕緣子串動張力分析

3.1.1 脫冰位置變化對絕緣子串動張力影響

為了研究不同脫冰位置對絕緣子串動張力的影響，本文仿真計算了10mm覆冰厚度、100%脫冰量工況下不同脫冰位置脫冰后50s內跨越檔右相導線對懸垂串的作用力，如圖5。

圖5 不同脫冰位置懸垂串動張力時程曲線

圖5中第1秒內為覆冰時導線對懸垂串的靜態作用力，第2s-50s為脫冰時導線對懸垂串的動態作用力。其中左側1/3檔脫冰為遠離懸垂串一側，右側1/3檔脫冰為靠近懸垂串一側。從圖中可以看出懸垂串動張力在脫冰初始時刻最大，隨著時間的推移震蕩呈遞減的趨勢，逐漸趨于某一穩定值。全擋脫冰懸垂串動張力波動幅值最大。相對于左右兩側脫冰，中間1/3檔脫冰絕緣子串動張力波動幅度較大，對金具受力影響較大。左側1/3檔脫冰與右側1/3檔脫冰兩種情況下懸垂串動張力時程曲線有差異。由于懸垂串處于跨越檔的右側，所以右側1/3檔脫冰對懸垂串的影響更大，脫冰初始時刻動張力略高于覆冰時靜態力。

3.1.2 脫冰量變化對絕緣子串動張力影響

為了研究不同脫冰量對絕緣子串動張力的影響，本文仿真計算了10mm覆冰厚度、全檔脫冰工況下不同脫冰量脫冰后50s內跨越檔右相導線對懸垂串的作用力，如圖6。

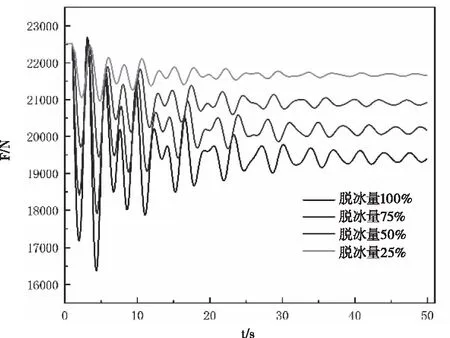
圖6 不同脫冰量懸垂串動張力時程曲線

分別計算了25%、50%、75%、100%四種不同脫冰量下絕緣子串動張力。從圖8中可以看出懸垂串動張力波動幅值隨著脫冰量的減少逐漸減小，脫冰量25%工況下懸垂串動張力波動幅值最小，但穩定后絕緣子串張力值最大。

3.1.3 覆冰厚度變化對絕緣子串動張力影響

考慮到導線脫冰跳躍在中冰區發生情況較多，中冰區為設計覆冰厚度大于10mm小于20mm的地區。因此，本文仿真計算100%脫冰量、全檔脫冰工況下不同覆冰厚度脫冰后50s內跨越檔右相導線對懸垂串的作用力，如圖7。

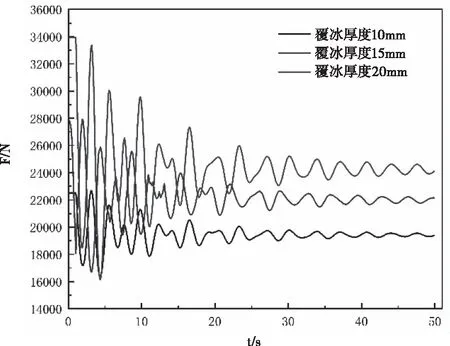
圖7 不同脫冰厚度懸垂串動張力時程曲線

分別計算了10mm、15mm、20mm三種脫冰厚度下絕緣子串動張力。從圖9中可以看出隨著覆冰厚度的增大，懸垂串動張力波動幅度逐漸增大，穩定后絕緣子串張力值也越大。其中20mm覆冰厚度工況下最大波動幅值在初始時刻達到了17kN。由此可知覆冰厚度增加使絕緣子串動張力幅值變化范圍增大，易造成絕緣子串金具破壞。

3.2 絕緣子串金具應力分析

絕緣子串金具鋼號為Q235b，抗拉強度為370～500MPa，安全系數為1.5，許用應力為247～333MPa。考慮到實際冰災中全擋脫冰發生概率較低，主要發生局部脫冰災害。中間1/3檔脫冰相對于左右兩側脫冰影響更大。因此選取覆冰厚度10mm情況下脫冰量75%中間1/3檔脫冰作為研究工況，將絕緣子串動張力等效施加在懸垂串實體有限元模型上，得到懸垂串連接金具中各個金具的受力計算結果，如圖8。

圖8 懸垂串金具應力分布云圖

如圖8所示，為懸垂串各典型金具仿真分析的應力云圖。其中圖(a)為ZBS掛板，(b)為球頭掛環，(c)為碗頭掛板，(d)為聯板，(e)為懸垂線夾U型掛環，(f)為懸垂線夾船體。

分析ZBS掛板應力云圖可知，脫冰過程中最大應力主要集中在ZBS掛板下端孔洞中，最大應力為53.99MPa。

分析球頭掛環應力云圖可知，脫冰過程中最大應力主要集中在球頭與直棒的連接處。球頭掛環受到的最大應力為181.77MPa。

分析碗頭掛板應力云圖可知，脫冰過程中最大應力主要集中在碗頭掛板下端連接螺栓的孔洞中，最大的應力為74.60MPa。

分析聯板應力云圖可知，脫冰過程中的最大應力主要集中在聯板孔洞中，最大應力為74.82 MPa。

分析懸垂線夾應力云圖，脫冰過程中U型掛環的最大應力主要集中在其下部U型處，最大應力為126.88 MPa。線夾船體的上下孔洞附近均出現了應力集中，最大應力為106.36MPa。

根據以上分析可知，各金具最大應力均未超過材料的許用應力。懸垂串球頭掛環在脫冰過程中的應力最大。最大應力出現位置(圖8紅圈處)與圖9現場實際拍攝圖片斷裂位置相同，也證明了本文仿真分析的正確性，說明懸垂串球頭掛環處需要重點關注。

圖9 球頭掛環球頭連接處斷裂

4 結論

本文以某220kV交叉跨越線路為工程背景，通過分段建模法建立“耐-直-耐”跨越線路的塔線系統有限元分析模型，采用ANSYS單元“生死”法模擬架空導線的脫冰過程，分析計算“耐-直-耐”跨越線路絕緣子串在不同脫冰情況下的動態響應。有以下結論。

1)全檔脫冰對絕緣子串動張力影響最大，動張力波動幅值大于局部脫冰。但實際冰災中全擋脫冰發生概率較低，主要發生局部脫冰災害。因此，研究局部脫冰跳躍對跨越線路造成的動態響應更有意義。相對于左右兩側脫冰，中間1/3檔脫冰絕緣子串動張力波動幅度較大，對金具受力影響較大。左側1/3檔脫冰與右側1/3檔脫冰兩種情況下懸垂串動張力時程曲線有差異。由于懸垂串處于跨越檔的右側，所以右側1/3檔脫冰對懸垂串的影響更大。對工程中確定安全脫冰的脫冰順序有所幫助。

2)覆冰厚度和脫冰量的增加均會造成絕緣子串動張力波動幅度增大，易造成絕緣子串金具破壞。

3)脫冰工況下懸垂串球頭掛環連接處受到的應力最大；和現場實際斷裂位置一致，需要重點關注；可在球頭和直棒相連位置進行加厚處理，安全系數由1.5提高到1.7，能有效降低絕緣子串金具破壞風險。