基于改進PF的鋰電池RUL預測比較研究

冀超驥，袁學慶，張 陽

(1. 中國科學院沈陽自動化研究所，遼寧 沈陽 110016；2. 中國科學院機器人與智能制造創新研究院，遼寧 沈陽 110169；3. 中國科學院大學，北京 100049)

1 引言

鋰離子電池相比鉛酸和鎳氫等電池具有高能量密度、低記憶效應且環境友好等優勢，從手機、筆記本電腦等便攜式消費電子設備到混合動力汽車、航空航天領域，目前其都是理想能源。然而，使用中的電池受內外部環境負載的影響其性能會逐漸退化，具體表現為容量衰退及內阻增加，隨之其壽命逐漸衰減直至最終失效。鋰離子電池作為動力來源，是設備正常運轉和系統功能實現的關鍵，其出現失效的后果可能從帶來不便到災難性故障和大型任務的失敗，隨著鋰電池應用的增加，其在使用中的故障預測和健康管理(prognostic and health management，PHM)受到了更多研究人員的關注。電池健康管理的三個關鍵內容是荷電狀態(state of charge，SOC)估計、健康狀態(state of health，SOH)估計和剩余壽命(remaining useful life，RUL)預測。RUL可以定義為電池從當前工作狀態至其壽命達到終止前所能經歷的充放電循環次數。通過有效預測RUL，可使電池在失效之前提前更換，實現自主預防性維護，提高系統可靠性。

近年來，針對鋰離子電池RUL預測的研究主要圍繞基于性能的方法展開，通過估計電池性能，如當前電池實際容量的衰退情況，判斷電池充滿電后的容量能否滿足可保證電池正常工作的閾值要求，將對RUL的預測轉化為對容量的預測，獲得RUL預測結果。基于性能的鋰電池RUL預測方法可分為模型法、數據驅動法及融合型方法。基于模型的RUL預測所用模型又分為退化機理模型、等效電路模型和經驗退化模型。其中，經驗退化模型無需考慮電池內部的物理化學特性，轉而從數據角度出發，通過描述電池內部能夠代表電池性能退化的狀態量隨時間變化的規律或描述前后兩個時刻狀態量之間的關系，實現電池退化特征的模型表達。基于經驗退化模型實現電池RUL預測，一般是利用濾波算法對電池退化信息進行跟蹤，針對特定狀態采集數據，求出模型的最優化參數完成模型構建，再基于模型進行狀態濾波。因此，基于經驗退化模型的預測又被稱為基于統計濾波的預測。廣泛使用的統計濾波算法主要有卡爾曼濾波、粒子濾波及與其相關的優化算法。

基于經驗退化模型，利用粒子濾波(particle filter，PF)算法進行鋰電池RUL預測的統計濾波方法，由于能夠適應非線性、非高斯的狀態預測并可提供預測結果的不確定性表達，在實際中應用廣泛。但是，PF本身存在不可避免的粒子退化問題，即算法經過數次迭代后，許多粒子的權重變得很小，只有少數粒子的權重較大，使大量計算浪費在對后驗概率估計幾乎不起作用的粒子上導算法性能下降。采樣重要性重采樣粒子濾波(sampling importance resampling PF，SIR-PF)引入的重采樣過程雖然可以減小粒子退化影響，但又會導致粒子多樣性降低，即最后所有粒子可能都由同一個大權值的粒子復制而來，影響預測精度。除增加粒子數和重采樣之外，減小粒子退化影響的重要途徑是選擇合適的重要性概率密度函數使粒子間的方差更小。因此，本文將通過兩個途徑對基于PF算法進行鋰電池RUL預測的方法做出改進：①選擇合適的建議分布進行重要性采樣；②免重采樣。

2 鋰離子電池容量雙指數經驗退化模型

2.1 鋰離子電池容量退化現象

與其它二次電池一樣，鋰離子電池的實際容量會隨充放電循環次數的增加而衰減，且不可避免，RUL隨之減少，造成這種現象的主要原因有過充、自放電、電解質還原、金屬鋰沉積、活性物質溶解等。

本研究使用NASA公開的鋰電池數據集，該數據集在環境溫度25℃下由18650電池獲取，電池失效閾值取1.38Ah。對所需數據進行提取后，在matlab中繪制編號B0005、B0006、B0007和B0018四組電池的容量退化曲線如圖1。

圖1 電池容量退化曲線

2.2 鋰離子電池容量退化模型的構建

通過統計濾波方法預測鋰電池RUL，需要確定濾波過程所基于的電池容量退化模型。目前廣泛使用的電池容量雙指數經驗退化模型對于電池容量的非線性退化特征跟蹤效果較好，其形式如下

=·exp(·)+·exp(·)

(1)

其中，代表周期數，電池的一次充放電是一個循環周期；是第周期的電池容量；，，，是需要進行參數擬合的未知參數。

為驗證模型可行性，首先借助matlab曲線擬合工具箱進行模型參數擬合。由于編號B0007的電池在實驗周期結束時容量仍未達到失效閾值，這里取B0005、B0006和B0018三組電池的參數擬合結果見表1。

文獻[2]采用常用評價指標：和方差(SSE)、確定系數(R)、調整確定系數(Adjusted R)和均方差(RMSE)評價模型擬合結果的優劣，表明了雙指數經驗退化模型能夠有效描述鋰電池容量的退化趨勢。

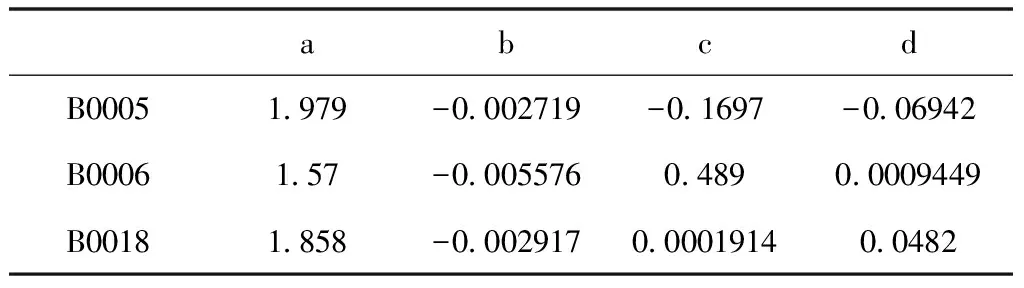
表1 模型參數擬合結果

從曲線擬合工具箱得到的a，b，c，d參數值經過一定處理后可作為初始模型參數，完成對電池容量退化模型的構建。本研究將以B0005電池數據作為實驗對象，為減少特殊參數的影響，這里使用平均值法，即取三組電池擬合結果的平均值作為B0005電池容量退化模型的初始參數，，，，計算結果如下：

=18023；=-00037；=01065；=-00068。

3 粒子濾波及其相關改進算法

PF在實際應用中存在“粒子退化”問題，減小粒子退化影響的主要措施有增加粒子數、重采樣和選擇合適的重要性采樣概率密度函數(又稱建議分布)。

增加粒子數的方法最為簡單直接，但粒子數的增加也意味著計算量和時間消耗的增加。重采樣的思想是將權值較小的粒子剔除，對權值較大的粒子依據其權值大小按比例復制，即權值大的多復制，從而構成新的粒子集，各粒子的權值均為1/N。文獻[12]中介紹并比較了四種重采樣方法。選擇合適的重要性概率密度函數是克服粒子退化的又一重要途徑。

3.1 SIR粒子濾波

SIR-PF在PF的權值歸一化步驟后加入了重采樣的操作，并對建議分布做出特定的選擇，即

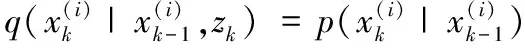
(2)

SIR-PF選取(2)式丟失了當前時刻的測量值，使當前狀態值嚴重依賴于模型，如果模型不準確或測量噪聲突變，則這種選取將不能有效表示后驗概率的真實分布。解決辦法可以是使用利用無跡卡爾曼濾波(unscented kalman filter，UKF)將最近的測量信息計入建議分布的無跡粒子濾波(unscented particle filter，UPF)。同時，選擇好的重要性概率密度函數也可減少粒子退化現象，選擇標準是使采樣粒子之間的權值方差更小。

3.2 無跡粒子濾波(UPF)

已知一個動態系統有如下形式的狀態方程和觀測方程

=(-1，-1)

=(，)

，是獨立同分布的過程噪聲和測量噪聲，～(0，)，～(0，)。

的具體步驟如下：

321 初始化

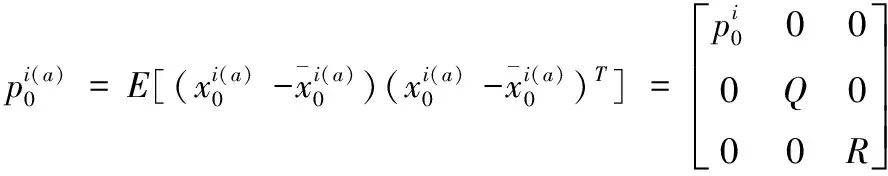
322 對每個周期=1：

1) 重要性采樣

對每個粒子=1：，通過獲得更新值：

①計算sigma點集

取2+1個點為

②時間更新

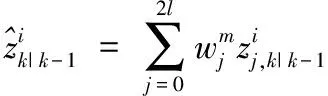
③測量更新

④用UKF運行結果得到的均值和協方差進行重要性采樣

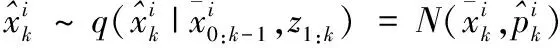
2) 計算個粒子的權值

3) 歸一化個粒子的權值

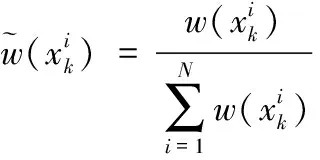
4) 重采樣

5) 計算狀態估計值并輸出

這里的步驟是按照后續實驗實際使用的步驟給出的，即對粒子權值歸一化后，先重采樣使權值變為1再求狀態量的平均值。

3.3 高斯粒子濾波(GPF)

重采樣能夠克服粒子退化現象，但是重采樣也會帶來新的問題，最后所有粒子可能都是同一個大權值粒子的子代，粒子總體的多樣性降低，不足以用來近似表征后驗概率密度，即出現“樣本貧化”。現有的各種改進粒子濾波算法仍未能很好地解決重采樣過程中計算量較大、出現樣本枯竭而導致濾波發散的問題。

為了保證粒子多樣性，研究人員又提出了重采樣-MCMC算法、權值選擇粒子濾波等改進了重采樣步驟的方法預測鋰電池RUL。本研究則選擇從“免重采樣”的思路入手，提出將改進的高斯粒子濾波(improved gaussion particle filter，GPF)應用于鋰電池RUL預測。

高斯粒子濾波(gaussion particle filter，GPF)是用高斯分布去近似后驗分布，本質上是利用重要性采樣去近似未知狀態變量的后驗均值和協方差。與一般的粒子濾波相比，只要所用的高斯分布是正確的，就不會產生粒子退化問題，因此無需重采樣，從而降低了算法在原理和實現過程上的復雜度。

GPF算法步驟如下：

1) 量測更新

①重要性采樣

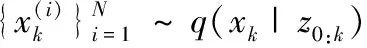
②計算粒子權值

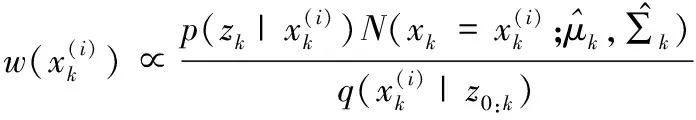
③粒子權值歸一化

④估計狀態后驗概率密度(|0：)的均值和協方差

2) 時間更新

①從量測更新階段估計的后驗分布采樣

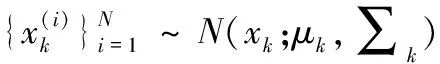
②計算預測粒子集：

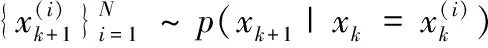
③計算預測粒子集的均值和協方差

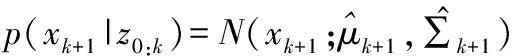
3.4 改進的高斯粒子濾波(IGPF)

4 實驗

實驗將以0005電池數據為基礎，將對鋰電池RUL的預測轉換為對電池在某個循環周期實際容量的預測。以(1)式的參數[a，b，c，d]作為系統狀態量，選取不同的起始預測周期，在該周期前分別利用SIR-PF、UPF和IGPF進行模型參數更新，在該周期后參數不變，用這些參數建立電池容量退化模型，預測后續周期的電池容量，得到電池容量退化至失效閾值容量時對應的周期，進而得出鋰電池RUL。具體步驟如下：

4.1 模型參數更新

1) 將12節中計算的，，，作為初始模型參數，即=[，，，]。

2) 建立鋰電池系統狀態方程和測量方程如下

=[，，，]

在實驗中取

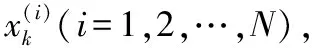
4) 以起始預測周期=81、為例，某次實驗對模型參數的更新情況如圖2，具體參數更新結果為

=18023，=-00022，=01076，=-00071

后續周期將使用這組參數進行容量預測。

圖2 IGPF更新的模型參數

4.2 鋰電池容量和RUL預測

1) 在起始預測周期=81之后的周期，模型參數不再變化，將=81時的參數代入容量退化模型計算當前周期的電池容量預測值。起始預測周期后第個周期的容量計算表示為：

+=·exp[·(+)]+·exp[·(+)]

在程序中可以通過循環逐一計算后續各周期所對應的電池容量。

2) 找出失效周期。本實驗中是選取電池容量未低于失效閾值1.38Ah的最后一個周期作為電池壽命截止周期，用PEL(Prediction of End of Life)代表該周期的預測值，REL(Real End of Life)代表已知數據集中實測容量值對應的失效周期，求解PEL可用下式表示

138>·exp[·(+1)]+

·exp[·(+1)]

使用SIR-PF、UPF和IGPF的電池容量跟蹤和預測曲線如圖3。

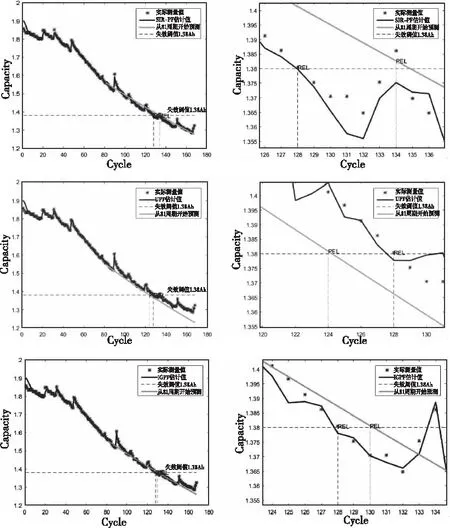
圖3 鋰電池容量跟蹤與預測曲線

3) 計算鋰電池RUL、預測誤差error(cycle)

=-(+)

()=-

4) 取不同的起始預測周期k=71、k=81和k=101，分別使用SIR-PF、UPF和IGPF進行10次失效周期的預測，計算預測誤差的均值和方差進行比較分析。具體數據見表2。μ和∑分別代表預測結果誤差的均值和方差。表中的/兩側分別代表取誤差絕對值求和與直接將誤差求和的結果。

5) 計算SIR-PF、UPF和IGPF預測結果的不確定性表達，繪圖并進行比較分析。本研究在實驗中發現預測階段直接代入起始預測周期的狀態量濾波結果，即用一個確定的向量=[，，，]去計算容量，實現簡單，且尤其對于新提出的IGPF算法得到的預測結果分布更穩定、精度更高。這里為給出粒子集預測結果的后驗概率分布，也使用起始預測周期的粒子集計算容量和RUL。

表2 N=100時不同起始周期各算法誤差

計算起始預測周期k后第m周期的預測容量：

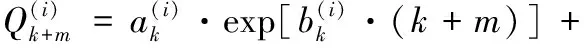
計算預測容量的均值

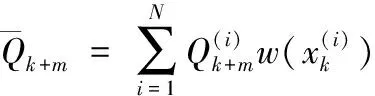
計算起始預測周期粒子集對應的失效周期

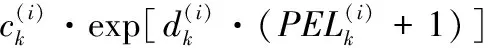
計算失效周期的均值

計算剩余壽命的均值

計算剩余壽命的后驗概率密度函數

以粒子數N=100，起始預測周期k=101，預測失效周期結果為129為例，使用SIR-PF、UPF預測RUL的概率密度和IGPF預測RUL的概率密度及不同RUL預測結果對應的原始粒子數分布如圖4所示。

圖4 RUL的概率密度及IGPF的原始粒子分布

說明：從RUL預測結果的概率密度圖可知UPF比SIR-PF的粒子退化程度小，具體表現為pdf的寬度窄、峰值高，說明權重偏小的無效粒子更少。而IGPF的圖像較為特殊，每次實驗均有約1/3數量的粒子計算所得到的容量值在實驗結束周期(第168周期)仍未達到失效閾值，經實驗發現如將它們的失效周期定為168加權計算的預測結果精度已足夠高，其它粒子預測值分布均勻，由于免重采樣所以無粒子貧化現象，且最終結果可以有效預測RUL。

5 結論

研究通過理論分析和實驗驗證，表明UPF和IGPF均能夠有效預測鋰電池RUL，預測結果誤差的方差均比SIR-PF小。其中，UPF預測誤差的均值最小，IGPF運行速度則更快，且誤差全在大于0的一側，預測結果更加穩定。

總結如下：

1) UPF：使重要性采樣的粒子方差變小，可以抑制粒子退化現象。

2) IGPF：免重采樣避免了粒子貧化現象，具有運行速度快、精度高且易實現的優勢。