準Z源光伏逆變直流鏈電壓積分滑模控制仿真

胡潤滋，古濟銘，趙 科，何立婧

(1. 國網重慶市電力公司電力調度控制中心，重慶 400014；2. 重慶大學輸配電裝備及系統安全與新技術國家重點實驗室，重慶 400044)

1 引言

由于光伏輸出直流電壓的變化范圍較大，而準Z源逆變器(quasi-Z-source inverter，qZSI)具有可以升降壓，輸出電壓調節范圍大、輸出波形畸變小以及允許逆變橋短路或開路等特點，因此被廣泛應用到光伏系統中。

滑模控制作為一種非線性控制方法，具有良好的魯棒性和自適應性，在電力電子變換器的控制中得到了廣泛的研究。文獻[8]提出了一種單相Z源網絡的電壓紋波前饋控制策略，調制系數通過電壓紋波前饋控制進行校正，為了解決重載條件下直流母線輸出電壓波動范圍較大的問題，所提出的控制策略明顯削弱了直流鏈電壓紋波對交流側波形的不良影響，但當電源輸出電壓變化范圍較大時，系統響應速度較慢。文獻[9]提出了一種Z源網絡直流鏈電壓直接控制策略，設計了一種經典PID補償器，但由于增加了方波檢測電路，增加了系統的成本，在實際應用中較多采用間接控制。文獻[10]采用電感電流和電容電壓作為狀態變量，對Z源直流鏈電壓進行滑模控制，但沒有對電流進行積分，輸出響應較慢，電壓超調較大。

本文提出了一種應用于準Z源網絡的帶電流積分滑模控制方法，準Z源固有的右半平面零點的存在使控制器的設計變得復雜，同時限制了電壓模式控制器補償網絡的帶寬。采用的狀態變量為電感電流誤差、電容電壓誤差以及它們誤差的積分，使變換器動態響應快，電壓超調相對較小，跟蹤參考信號性能好，選擇間接控制方法來控制直流鏈的電壓值。測試了在負載擾動下的魯棒性，通過Simulink仿真表明，在光伏板輸出隨負載非線性變化條件下，所設計的滑模控制器能夠更好的跟蹤參考信號，具有魯棒性強，保證系統穩定的特點。

2 準Z源逆變器的基本原理

傳統的逆變電路可分為電壓型和電流型逆變電路。準源逆變器的系統結構如圖1。電感、和電容、構成源網絡，逆變橋式電路由6只開關管～組成。插入直通時間來控制逆變電路的升降壓，可使>實現升壓。根據電感伏秒平衡可得

直流輸入電壓和直流鏈電壓的關系為

(1)

直流輸入電壓和電容電壓的關系為

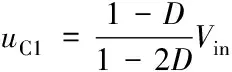
(2)

直流輸入電壓和電容電壓的關系為

(3)

其中表示直流輸入電壓，表示直流鏈電壓，表示電容電壓，表示直通占空比，在0<<05的條件下，逆變器就能實現升壓。

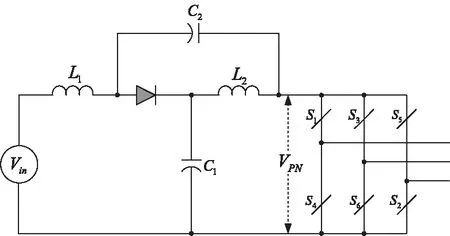
圖1 三相準Z源逆變器拓撲

3 準Z源的數學模型

3.1 大信號模型

令==，==。

1)直通狀態

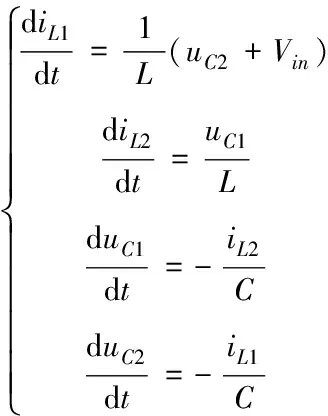
2)非直通狀態

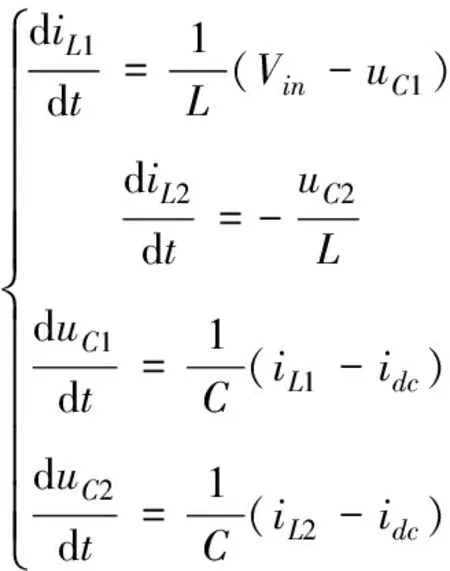
3.2 狀態空間模型

(4)

其中

4 電流滑模控制器的設計

假定準Z源逆變器(qZSI)工作在連續電流模式(CCM)，下面詳細介紹滑模控制器的設計過程。

4.1 滑模面設計

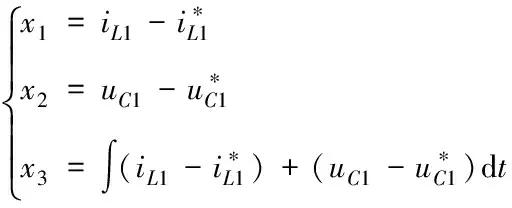
(5)

選擇滑模面

=++=

(6)

則

4.2 推導等效控制律

對求導得

(7)

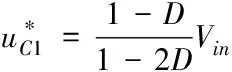
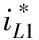
(8)

其中，為積分系數，為比例系數。

把式(8)代入式(7)得

(9)

(10)

其中:=+(-1)；=(-)；=。

圖2所示為的整體控制框圖，等效控制律是一個連續量，與直通占空比等效，值域為[0，05)。

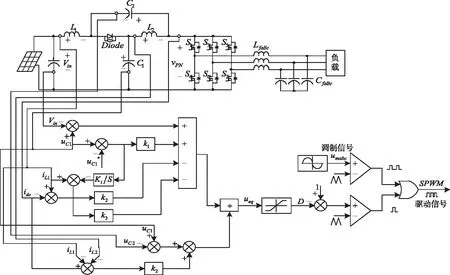
圖2 qZSI整體控制框圖

4.3 存在條件

根據滑模控制理論，所設計的直流鏈電壓帶電流積分滑模控制器應在系統所有輸入和負載條件下均滿足到達、存在和穩定性3個條件。

控制器采用的控制律

當<0，=1時，由源變換器的原理可知，直通占空比≤05，結合式(2)，此時1→∞，通過(6)定義可使滑模面滿足到達條件。

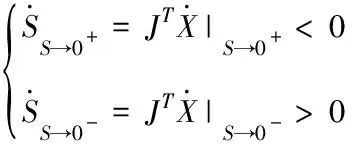
上式可分為兩種情況

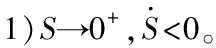
用u=0替換u→0，代入式(9)得

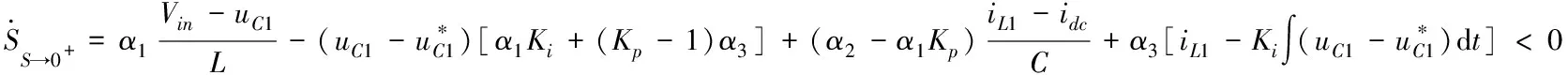
(11)

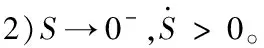
用u=1替換u→0，代入式(9)得

(12)

其中，和為已知參數；、1和2的值在一定范圍內波動，因此，有必要考慮其值的臨界點。如果最大或最小工作狀態滿足存在條件，則整個工作狀態滿足存在條件。1、2和都為瞬時狀態變量，設計過程較復雜，把狀態變量1、2和用期望設計的穩態值代替，為1()、2()和()。此方法能夠讓系統在小范圍內滿足存在條件。即存在條件如下式

(13)

4.4 穩定條件

首先推導系統的理想滑模動態，隨后進行平衡點分析，最后推導維持穩定的條件。

1)理想滑動動態

對于模式的系統，用u代替式(4)中的u，將不連續系統轉換為理想滑模連續系統，即

(14)

將等效控制信號u的表達式(10)代入上式得

(15)

上式表示帶電流積分滑模控制的理想滑動動態。

2)平衡點分析

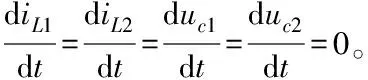
(16)

3)理想滑動動態的線性化

將理想滑動動態在平衡點附近線性化

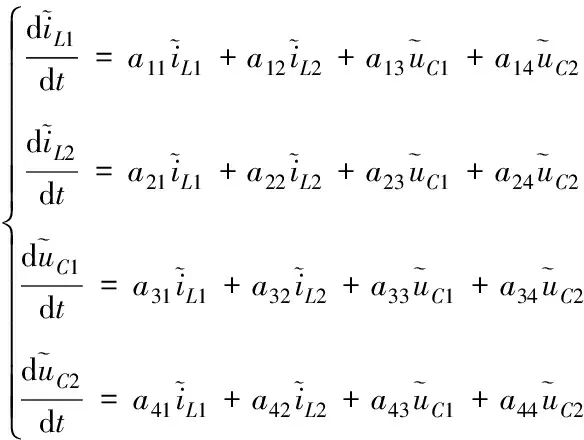
(17)

上式為式(15)的交流項，令

線性化系統化的特征方程為

|-|=0

(18)

其中，為特征系數矩陣，為單位矩陣。式(18)確定了系統的動態特性和穩定性，如果的全部極點在左半平面，那么系統在所設計的閉環系統滑模面上穩定運行。由式(13)和式(18)來選擇滿足穩定運行的滑模系數。

5 仿真和實驗結果

5.1 光伏電池的建模

工程中光伏組件的工作特性主要采用單二級管等效電路來描述，如圖2。

圖3 光伏組件的單二極管等效電路

由圖3可以寫出光伏組件的數學表達式。

=--

(19)

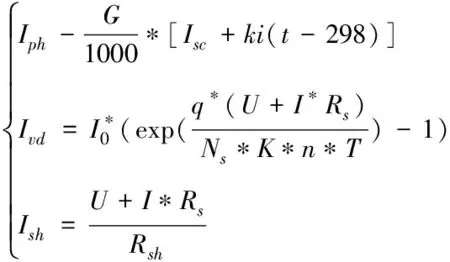
光伏組件的數學模型可以由以上表達式描述，其中參數的含義見表1。

表1 參數的物理意義及取值

參數設定值見表2。

表2 參數設置

根據上述公式在中搭建仿真模型，如圖4。

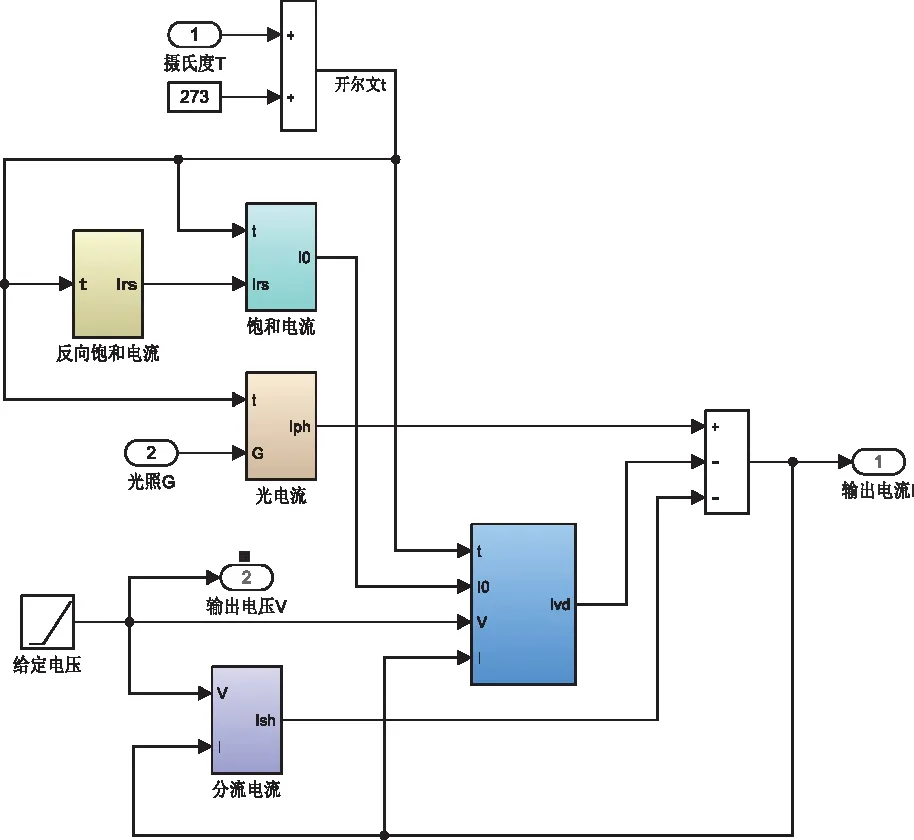
圖4 光伏組件的數學模型

光照強度為=1000的工作條件下，溫度在=25℃，=50℃，=75℃變化，仿真得到光伏電池的和曲線結果如圖4()，()所示。溫度為=25℃的工作條件下，光照強度在=600，=800，=1000變化，仿真得到光伏電池的和曲線結果如圖5()，()。

圖5 光伏電池的VI和PV曲線

5.2 準Z源網絡參數的選擇

準源網絡的參數設計過程在文獻[14]中進行了詳細的介紹。準源網絡工作在連續導電模式()。

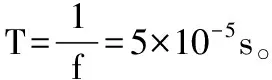
5.3 仿真結果

把設計的準源參數代入仿真模型中。在仿真中，用中光伏陣列模塊代替光伏電池。直流鏈電壓在滑模控制下的仿真電路圖如圖6。

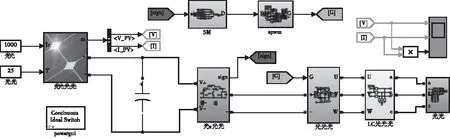
圖6 仿真電路圖

在負載擾動下，05時負載由=10609變成=5345。直流鏈電壓出現暫態過程，經過3左右的時間恢復了穩態值。直流鏈電壓峰值V、電容電壓V波形分別如圖7()和圖8()。

在無積分的傳統滑模控制器作用下，05時負載由RLoad=10.609Ω變成R=5.345Ω。直流鏈電壓峰值V、電容電壓V波形分別如圖7()和圖8()。

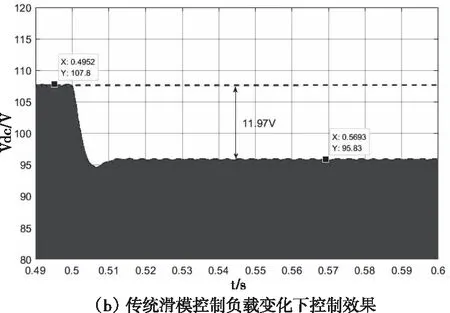
圖7 直流鏈電壓波形圖

可知，帶電流的積分滑模控制器仿真結果波形更好，能更好的跟蹤參考信號，表明滑模控制器設計的合理性。

圖8 電容電壓波形圖

逆變器輸出側的相電壓波形圖如圖9，經過濾波后的單相電壓波形圖如圖10。其中帶積分滑模控制負載擾動如圖()，無積分滑模控制負載擾動如圖()。

圖9 逆變后ab相波形圖

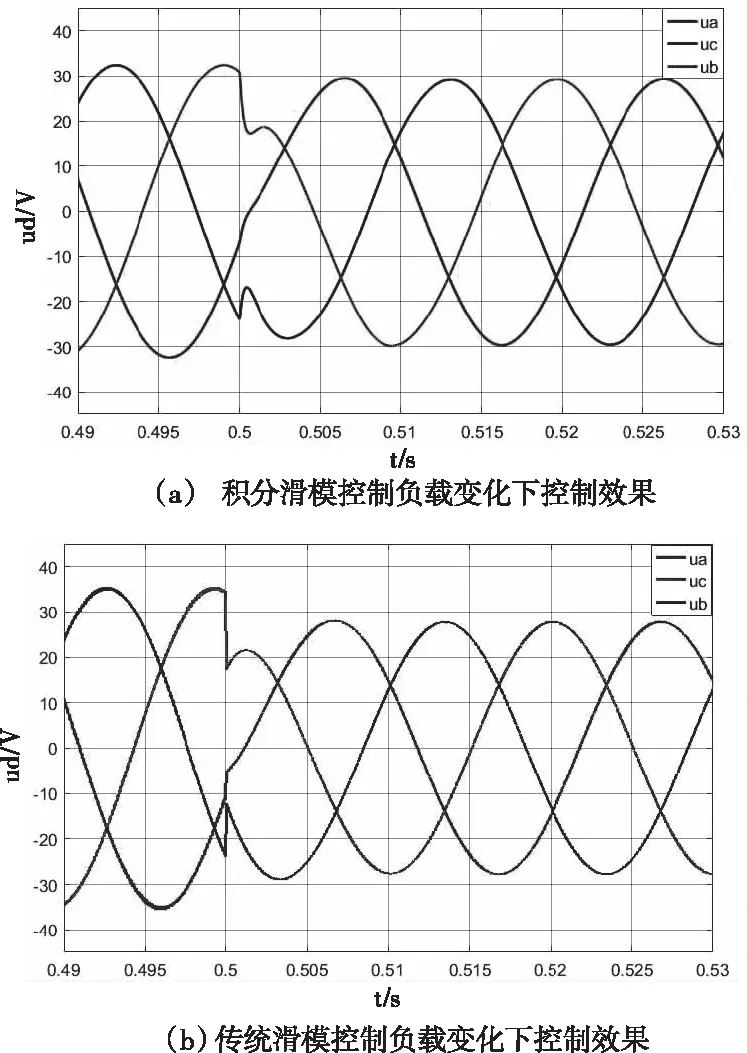
圖10 濾波后abc三相波形圖

6 結論