嵌入式大氣數(shù)據(jù)系統(tǒng)人工智能算法及故障診斷

張黎黎，王逸斌，趙 寧，劉學強

(南京航空航天大學 非定常空氣動力學與流動控制工業(yè)和信息化部重點實驗室，江蘇 南京 210016)

嵌入式大氣數(shù)據(jù)傳感(Flush Air Data Sensing，F(xiàn)ADS)系統(tǒng)采用分布在飛行器表面的壓力傳感器陣列，得到各測壓點的壓強值，然后通過特定解算算法計算出大氣數(shù)據(jù)(迎角α、側滑角β、馬赫數(shù)Ma等)。使用FADS系統(tǒng)測量大氣參數(shù)，與傳統(tǒng)的探針式大氣數(shù)據(jù)系統(tǒng)相比，維護成本較低，經(jīng)濟性良好。因此，被廣泛應用于航空航天領域。

從上世紀中葉起，美國國家航空航天局(National Aeronautics and Space Administration，NASA)就已經(jīng)開展了嵌入式大氣數(shù)據(jù)傳感系統(tǒng)的相關研究，并先后將其應用于諸多飛行器上(如：X-33，X-34，X-43a等)。NASA的德萊頓飛行中心最先研究了建立在X-15上的FADS系統(tǒng)的雛形，但該系統(tǒng)機械結構十分復雜，而且得到的結果也并不理想，故這種利用機械系統(tǒng)估算大氣參數(shù)的方法并不可行。而后在NASA的蘭利研究中心開展的SEDA(Shuttle Entry Air Data System)項目[1]中提出了通過安裝在飛行器機頭的傳感器測得的壓強值來反推大氣數(shù)據(jù)。20世紀90年代初，NASA在F-18大迎角氣動特性驗證機(High Alpha Research flight Vehicle，HARV)上安裝了大迎角嵌入式大氣數(shù)據(jù)傳感系統(tǒng)(High angle-of-attack Flush Air Data Sensing System，HI-FADS)，Whitmore等[2]提出了非線性回歸算法來估算大氣數(shù)據(jù)，并進行了飛行試驗。后來，在應用于X-33的嵌入式大氣數(shù)據(jù)系統(tǒng)的研究中，Whitmore等[3]提出了三點法來計算大氣數(shù)據(jù)。三點法是目前應用最為成熟的FADS算法，但該算法存在迭代不收斂的情況。21世紀初，Baumann等[4]開發(fā)了用于高超聲速飛行器(X-43a)的嵌入式大氣數(shù)據(jù)傳感系統(tǒng)，成功飛行了兩次，并且收集了飛行數(shù)據(jù)。20世紀末，Rohloff等[5-6]將神經(jīng)網(wǎng)絡應用于FADS系統(tǒng)算法，并且提出了容錯算法[7]，研究了基于神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法的噪聲魯棒性[8]。國內(nèi)一些學者如鄭成軍等[9]研究了BP神經(jīng)網(wǎng)絡在FADS系統(tǒng)中的應用。方習高等[10]提出了一種以馬赫數(shù)為分段依據(jù)的基于BP人工神經(jīng)網(wǎng)絡的FADS大氣數(shù)據(jù)解算算法。2015年，王逸斌等[11]基于Kriging算法提出了一種FADS系統(tǒng)計算模型，并與神經(jīng)網(wǎng)絡方法構建的模型進行了對比。2019年，王鵬等[12-13]研究了用于尖楔前體飛行器的嵌入式大氣數(shù)據(jù)傳感系統(tǒng)算法，構建了各大氣數(shù)據(jù)的神經(jīng)網(wǎng)絡模型，并且對算法進行了驗證和測試。2021年，王禹等[14]提出了適合工程應用的飛翼布局飛機的FADS算法模型，并對算法進行了仿真測試。

為實現(xiàn)對飛行器的精確控制，需獲得準確的大氣數(shù)據(jù)，故大氣數(shù)據(jù)系統(tǒng)應快速且準確地測量大氣參數(shù)。而神經(jīng)網(wǎng)絡方法具有很好的實時性，其自身具有一定的容錯能力，并且不會出現(xiàn)迭代不收斂的情況，而三點法計算大氣數(shù)據(jù)難以做到這些。故采用神經(jīng)網(wǎng)絡算法，以迎角和馬赫數(shù)為分段依據(jù)，開發(fā)了基于BP神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法，并對該算法進行了仿真測試，結果表明使用該算法預測各大氣參數(shù)能夠達到較高的精度。

FADS系統(tǒng)的故障檢測與管理自身具有一定的特殊性，如實時性較高、漏報率低，因為一旦引入故障數(shù)據(jù)可能會產(chǎn)生難以預估的后果。隨機森林算法常用于故障識別，但鮮有人將其應用于FADS系統(tǒng)故障識別。因而，將隨機森林算法用于FADS系統(tǒng)的故障診斷，采用隨機森林分類器快速準確地識別出故障測壓點，再將故障壓強剔除，使用構建的容錯神經(jīng)網(wǎng)絡計算大氣數(shù)據(jù)，降低了故障數(shù)據(jù)對FADS系統(tǒng)算法計算各大氣數(shù)據(jù)精度的影響。

1 算法流程概述

提出了以迎角和馬赫數(shù)為分段依據(jù)的基于BP神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法和基于隨機森林和神經(jīng)網(wǎng)絡的故障檢測與容錯算法，并且對該算法進行了仿真測試，圖1為算法流程圖。研究的FADS系統(tǒng)算法與故障識別與容錯算法適用于飛翼布局飛行器，該飛行器機身共分布有7個測壓點。首先，測壓傳感器測得的7個測壓點的壓強由事先構建的隨機森林分類器進行區(qū)分是否存在測壓點壓強故障的問題，若未出現(xiàn)故障，則由神經(jīng)網(wǎng)絡總模塊1初步計算迎角和馬赫數(shù)，然后由對應范圍內(nèi)的神經(jīng)網(wǎng)絡各分模塊計算各大氣參數(shù)(迎角、側滑角、馬赫數(shù)、靜壓Ps)。以7個測壓點壓強為輸入，其中：神經(jīng)網(wǎng)絡分模塊1為α=-4°～9°，Ma=0.1～0.4分段下的迎角、側滑角、馬赫數(shù)和靜壓的神經(jīng)網(wǎng)絡；神經(jīng)網(wǎng)絡分模塊2為α=-4°～9°，Ma=0.4～1.0分段下的各大氣參數(shù)的神經(jīng)網(wǎng)絡；神經(jīng)網(wǎng)絡分模塊3為α=9°～20°，Ma=0.1～0.4分段下各大氣參數(shù)的神經(jīng)網(wǎng)絡；神經(jīng)網(wǎng)絡分模塊4為α=9°～20°、Ma=0.4～1.0分段下的各大氣參數(shù)神經(jīng)網(wǎng)絡。若隨機森林分類器判斷出該壓強組合存在故障壓強，并識別出故障測壓點，則將故障測壓點壓強剔除，由相應的神經(jīng)網(wǎng)絡總模塊2(該模塊為以6個測壓點壓強為輸入，迎角和馬赫數(shù)為輸出的神經(jīng)網(wǎng)絡)初步計算迎角和馬赫數(shù)。初步計算出迎角和馬赫數(shù)后，可大致判斷其所在范圍，從而由對應范圍內(nèi)的不包含故障測壓點壓強的容錯神經(jīng)網(wǎng)絡各分模塊進一步計算各大氣參數(shù)(包括迎角和馬赫數(shù))。以6個測壓點壓強為輸入，其中：神經(jīng)網(wǎng)絡分模塊5為α=-4°～9°、Ma=0.1～0.4分段下的容錯神經(jīng)網(wǎng)絡；神經(jīng)網(wǎng)絡分模塊6為α=-4°～9°、Ma=0.4～1.0分段下的容錯神經(jīng)網(wǎng)絡；神經(jīng)網(wǎng)絡分模塊7為α=9°～20°、Ma=0.1～0.4分段下的容錯神經(jīng)網(wǎng)絡；神經(jīng)網(wǎng)絡分模塊8為α=9°～20°、Ma=0.4～1.0分段下的容錯神經(jīng)網(wǎng)絡。

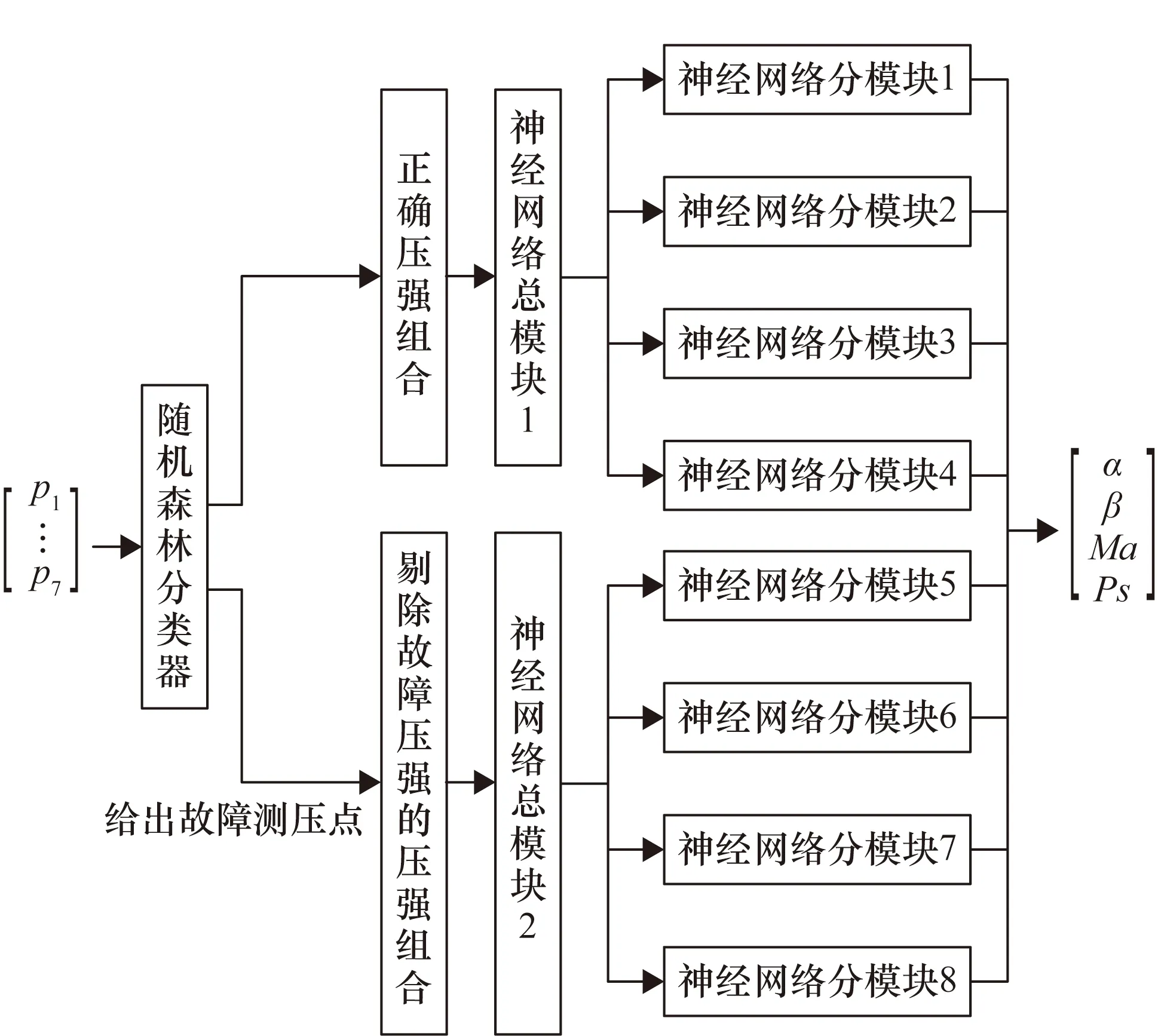
圖1 基于人工智能算法的嵌入式大氣數(shù)據(jù)傳感系統(tǒng)算法流程

由于容錯神經(jīng)網(wǎng)絡是以6個測壓點壓強為輸入構建的，所以提出的故障檢測和容錯算法能處理單個測壓點故障的情況，能夠有效降低單個測壓點故障對FADS系統(tǒng)計算大氣參數(shù)精度的影響。

2 基于BP神經(jīng)網(wǎng)絡的分段FADS系統(tǒng)算法

為提高神經(jīng)網(wǎng)絡預測大氣參數(shù)的精度，考慮將訓練數(shù)據(jù)以迎角(α=-4°～9°和α=9°～20°)和馬赫數(shù)(Ma=0.1～0.4和Ma=0.4～1.0)為分段依據(jù)分為4個部分。分別構建以7個測壓點壓強為輸入，迎角、側滑角、馬赫數(shù)、靜壓為輸出的神經(jīng)網(wǎng)絡。

使用MATLAB平臺的神經(jīng)網(wǎng)絡工具箱構建BP神經(jīng)網(wǎng)絡，使用LM(Levenberg-Marquardt)算法作為訓練算法，該算法收斂速度較快[15]。訓練時，訓練集占樣本總量的70%，驗證集和測試集分別占15%。并且構建的神經(jīng)網(wǎng)絡均只含有一個隱藏層，若誤差較大，則通過增加隱藏層神經(jīng)元數(shù)目和選用不同初始條件對網(wǎng)絡進行訓練來提高網(wǎng)絡的精度[16]。但增加隱藏層神經(jīng)元數(shù)目將會增加網(wǎng)絡訓練時間，而且可能會造成過擬合問題。

神經(jīng)網(wǎng)絡的訓練數(shù)據(jù)是由在實驗數(shù)據(jù)的基礎上構建的Kriging模型獲得的，采用共計394組實驗數(shù)據(jù)，以迎角、側滑角和馬赫數(shù)為輸入，各測壓點的壓強系數(shù)為輸出構建Kriging模型，采用構建的Kriging模型生成訓練神經(jīng)網(wǎng)絡所需的訓練數(shù)據(jù)，構建Kriging模型時均留有部分數(shù)據(jù)用于驗證模型精度。

表1～表4所示為構建的各分段下的迎角、側滑角、馬赫數(shù)以及靜壓神經(jīng)網(wǎng)絡的誤差區(qū)間以及均方根誤差。如表1所示，各分段下的迎角神經(jīng)網(wǎng)絡精度較高，其中3個分段下其精度可達0.2°，高馬赫、大迎角(α=9°～20°&Ma=0.4～1.0)分段下迎角神經(jīng)網(wǎng)絡的精度稍低，誤差在0.65°以內(nèi)。表2所示為各個分段下訓練得到的側滑角神經(jīng)網(wǎng)絡的誤差區(qū)間以及均方根誤差，各分段下的側滑角神經(jīng)網(wǎng)絡誤差以及均方根誤差與迎角相比稍大，小迎角分段下，構建的側滑角神經(jīng)網(wǎng)絡誤差以及均方根誤差更小。如表3所示，構建的各分段下的馬赫數(shù)神經(jīng)網(wǎng)絡均方根誤差量級可達10-5。如表4所示，各分段下的靜壓神經(jīng)網(wǎng)絡誤差均在200 Pa以內(nèi)，低馬赫數(shù)的分段下其精度更高，均方根誤差也很小。

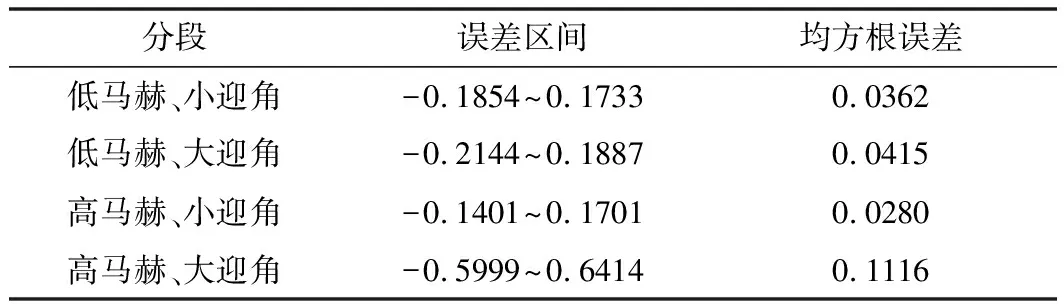
表1 各分段下迎角誤差區(qū)間及均方根誤差 單位：(°)

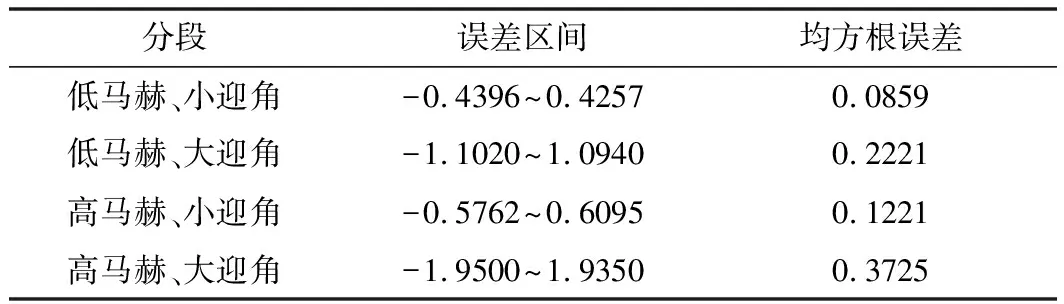
表2 各分段下側滑角誤差區(qū)間及均方根誤差 單位：(°)

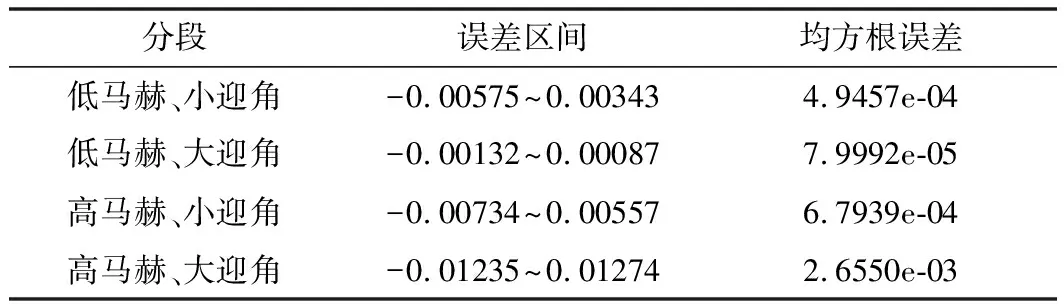
表3 各分段下馬赫數(shù)誤差區(qū)間及均方根誤差

表4 各分段下靜壓誤差區(qū)間及均方根誤差 單位：Pa

3 基于神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法測試

機器學習的主要挑戰(zhàn)是算法必須能夠在未學習到的新輸入上表現(xiàn)良好(這種能力被稱為泛化)[17]，而不只是在訓練集上表現(xiàn)良好，所以為了解構建的神經(jīng)網(wǎng)絡模型的泛化能力，采用飛行曲線數(shù)據(jù)，對開發(fā)的基于BP神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法進行了測試，同時測試了測壓點壓強有偏置時，各大氣數(shù)據(jù)的誤差情況。

3.1 分段神經(jīng)網(wǎng)絡仿真測試

用于仿真測試的飛行曲線數(shù)據(jù)共3023組，圖2～圖5分別為迎角、側滑角、馬赫數(shù)和靜壓的計算結果。將各大氣數(shù)據(jù)的真實值與計算值進行對比，圖6～圖9分別為迎角、側滑角、馬赫數(shù)和靜壓的相對誤差。圖2～圖9中橫坐標對應仿真數(shù)據(jù)中的每個狀態(tài)點。由圖2～圖9可知，每個飛行狀態(tài)下迎角誤差均小于0.2°，相對誤差小于0.7%；各狀態(tài)下側滑角誤差小于0.3°，大多數(shù)狀態(tài)點側滑角的計算誤差在0.1°以內(nèi)波動，相對誤差在1.5%以內(nèi)；馬赫數(shù)計算值與真實值吻合很好，絕對誤差均小于0.0105，相對誤差在1.1%以內(nèi)；靜壓誤差在300 Pa以內(nèi)，僅個別飛行狀態(tài)下誤差大于200 Pa，絕大多數(shù)狀態(tài)點靜壓誤差在100 Pa以內(nèi)，其相對誤差小于0.35%。

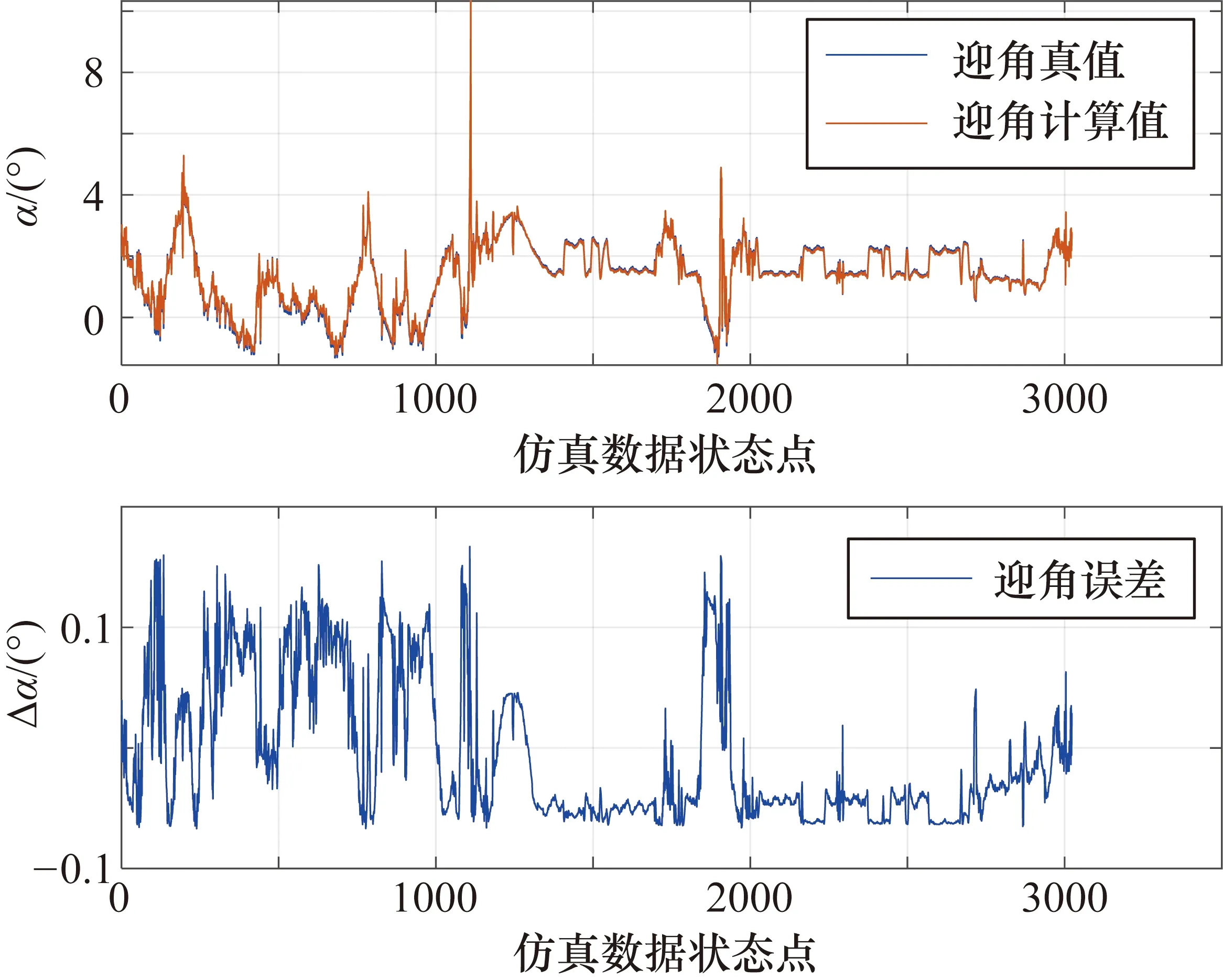
圖2 迎角計算結果

圖5 靜壓計算結果

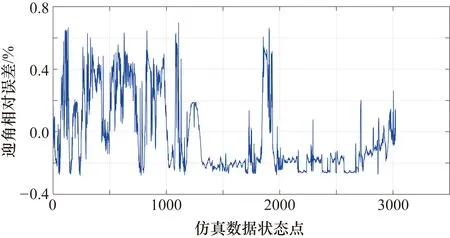
圖6 迎角相對誤差

圖7 側滑角相對誤差

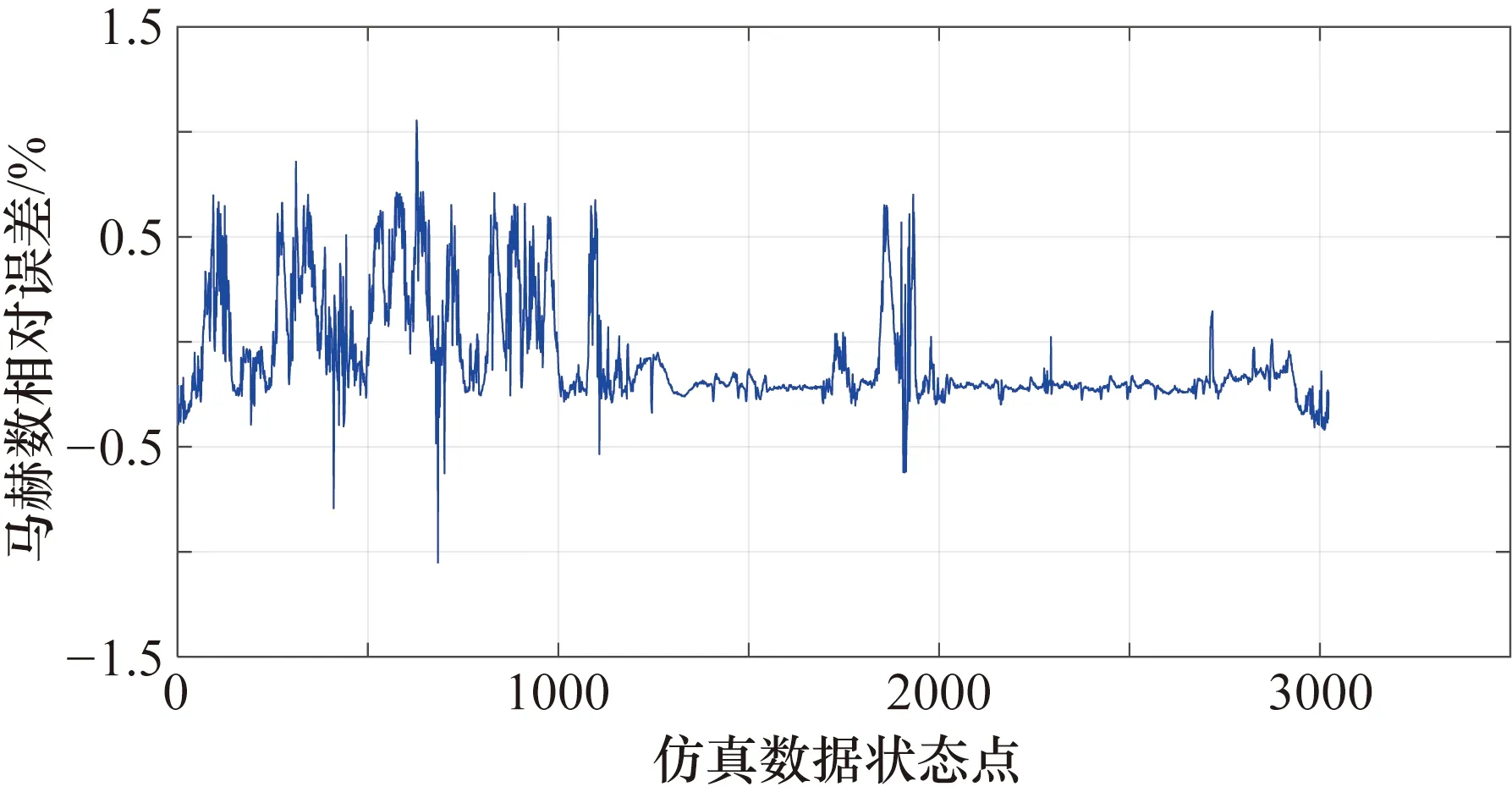
圖8 馬赫數(shù)相對誤差

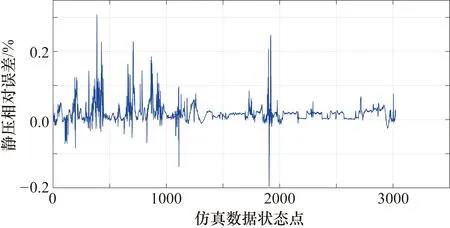
圖9 靜壓相對誤差

仿真結果表明：以迎角和馬赫數(shù)為分段依據(jù)，開發(fā)的基于BP神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法能夠快速準確地計算出各大氣數(shù)據(jù)，能夠滿足飛翼飛機FADS系統(tǒng)解算要求。

3.2 單個測壓點壓強偏置各大氣數(shù)據(jù)預測情況

由于測壓點的傳感器通常存在一定的誤差(一般的壓強傳感器的相對誤差為0.1%)，傳感器誤差可能會導致神經(jīng)網(wǎng)絡的輸入壓強與真實的壓強值出現(xiàn)微小的偏差，從而導致輸出的大氣數(shù)據(jù)產(chǎn)生誤差。本節(jié)人為增加駐點壓強偏差模擬測壓傳感器的誤差，研究這種情況下該算法計算出的大氣數(shù)據(jù)的誤差是否滿足要求。因此本節(jié)測試了單個測壓點壓強存在偏置(偏置100～400 Pa，每間隔100 Pa)時，基于BP神經(jīng)網(wǎng)絡的FADS系統(tǒng)算法計算大氣數(shù)據(jù)的準確性情況。限于篇幅，只給出駐點壓強偏置時，該算法計算迎角的結果。

圖10(a)～圖10(d)為測壓點7(駐點)壓強偏置分別為100～400 Pa時，F(xiàn)ADS系統(tǒng)算法預測迎角的情況。測壓點7壓強偏置100 Pa時，迎角誤差比壓強無偏置時略增大，壓強偏置至400 Pa時，其最大誤差超過0.2°。壓強偏置越大，迎角預測誤差越大，但仍滿足飛翼布局飛機對大氣數(shù)據(jù)的精度要求。這說明該FADS系統(tǒng)算法自身就具有一定的容錯能力。

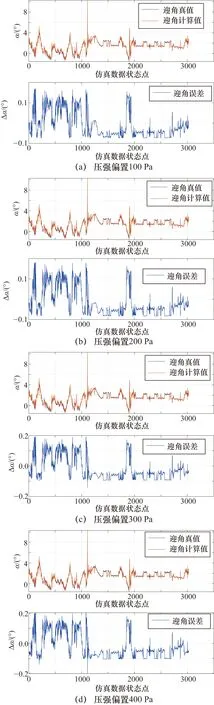
圖10 測壓點7不同壓強偏置迎角計算結果

4 故障診斷與容錯算法

4.1 隨機森林分類器

基于隨機森林分類器開發(fā)了測壓點故障診斷算法，同時構建了單個測壓點故障時，排除故障測壓點后僅采用6個測壓點壓強為輸入的神經(jīng)網(wǎng)絡，使該系統(tǒng)具備故障識別與容錯能力。假定測壓點壓強絕對誤差大于等于500 Pa，則認為該測壓點故障，使用隨機森林分類算法對錯誤壓強組合和正確壓強組合進行分類并識別出故障測壓點。本節(jié)構建的隨機森林分類器采用決策樹的個數(shù)為500，分裂屬性集中的屬性個數(shù)設為2。所有數(shù)據(jù)共包括正確壓強組合6020組，錯誤壓強組合84280組。從其中隨機選取90000組數(shù)據(jù)作為訓練數(shù)據(jù)，剩余300組數(shù)據(jù)作為測試數(shù)據(jù)。測試結果顯示，構建的隨機森林分類器能夠較為準確地將300組測試數(shù)據(jù)中的壓強正確分類，并且能夠較為準確地識別出故障壓強點，300組測試數(shù)據(jù)中，該分類器僅誤報一組壓強(將無故障誤報為測壓點7故障，此時測壓點存在500 Pa壓強誤差)，其余299組皆分類正確。

4.2 容錯神經(jīng)網(wǎng)絡

容錯神經(jīng)網(wǎng)絡依然采用分段神經(jīng)網(wǎng)絡提高網(wǎng)絡預測精度，目前算法中涉及的容錯神經(jīng)網(wǎng)絡以6個測壓點壓強為輸入，能夠處理單個測壓點故障，當將故障測壓點壓強剔除后，使用對應的不包含故障測壓點壓強為輸入的神經(jīng)網(wǎng)絡初步計算迎角和馬赫數(shù)，然后根據(jù)迎角和馬赫數(shù)的范圍采用對應分段下不包含故障測壓點壓強的神經(jīng)網(wǎng)絡進一步計算各大氣參數(shù)。

表5為不同輸入情況下迎角神經(jīng)網(wǎng)絡預測誤差及均方根誤差，任何一個傳感器出現(xiàn)故障，經(jīng)隨機森林分類器識別并剔除后，采用不包含故障壓強的正確壓強組合作為輸入，對各大氣參數(shù)進行預測。

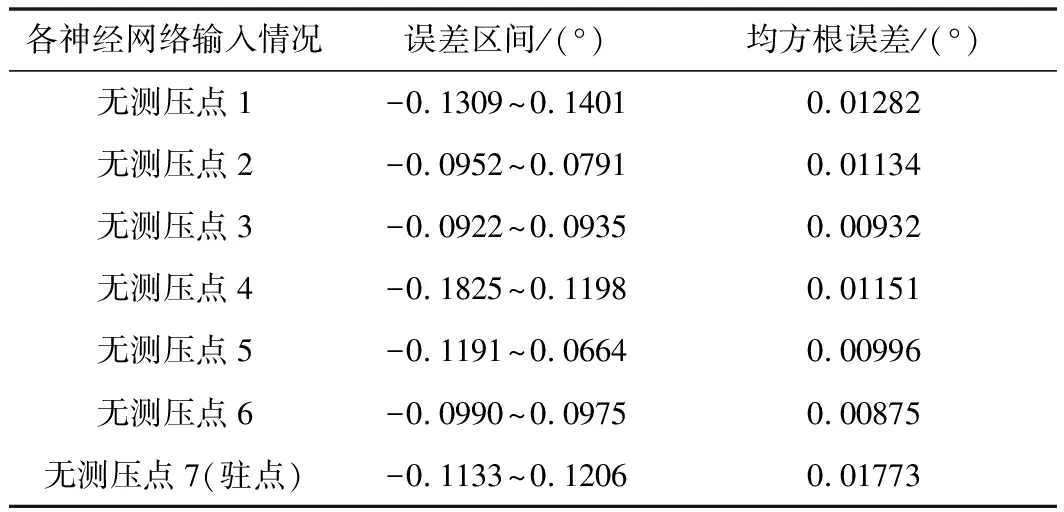
表5 不同輸入情況下迎角神經(jīng)網(wǎng)絡預測誤差及均方根誤差

4.3 故障檢測仿真測試

為測試基于隨機森林分類器和容錯神經(jīng)網(wǎng)絡的故障識別與容錯算法的可靠性和計算大氣數(shù)據(jù)的準確性，對于故障識別模塊，分別訓練了決策樹和隨機森林分類器，對比了兩種分類算法訓練得到的分類器的故障識別能力。

本節(jié)中采用的測試數(shù)據(jù)為飛行曲線中單個測壓點壓強偏置1500 Pa和2000 Pa(共計42組，包含7個不同測壓點壓強故障的情況)。飛行曲線測試結果顯示，構建的隨機森林分類器能夠準確識別出故障測壓點，準確率高達100%。而決策樹準確率也較高，但略遜于隨機森林分類器，42組數(shù)據(jù)中，訓練出的決策樹有一組數(shù)據(jù)識別錯誤，出現(xiàn)了誤報的情況。

圖11～圖18為使用隨機森林分類器識別故障測壓點，然后剔除故障壓強，采用有效壓強計算大氣數(shù)據(jù)的結果。圖11中的迎角計算值1和差值1為采用了開發(fā)的基于隨機森林的故障識別和容錯算法所計算得到的結果；迎角計算值2和差值2為未采用故障識別和容錯算法得到的結果；迎角真值為選取的測試數(shù)據(jù)的迎角真實值。從圖11中可以看出采用了故障識別系統(tǒng)的迎角計算結果與迎角真實值吻合較好，其誤差基本在0°附近；而未采用故障識別系統(tǒng)的迎角計算結果與迎角真實值相距甚遠，誤差較大，最大誤差甚至可達20°。圖12為采用故障檢測系統(tǒng)的迎角計算值與真實值的具體吻合情況，從該圖中可以看到，其最大誤差小于0.15°，迎角計算值較為準確。

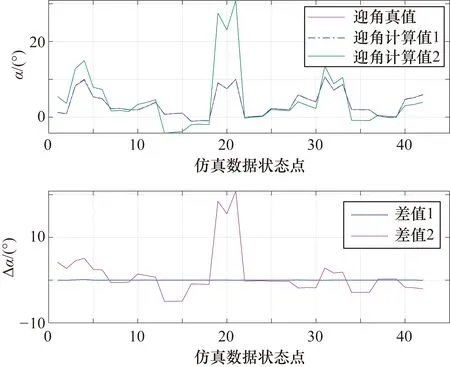
圖11 使用故障檢測系統(tǒng)和不使用故障檢測系統(tǒng)的迎角計算結果對比

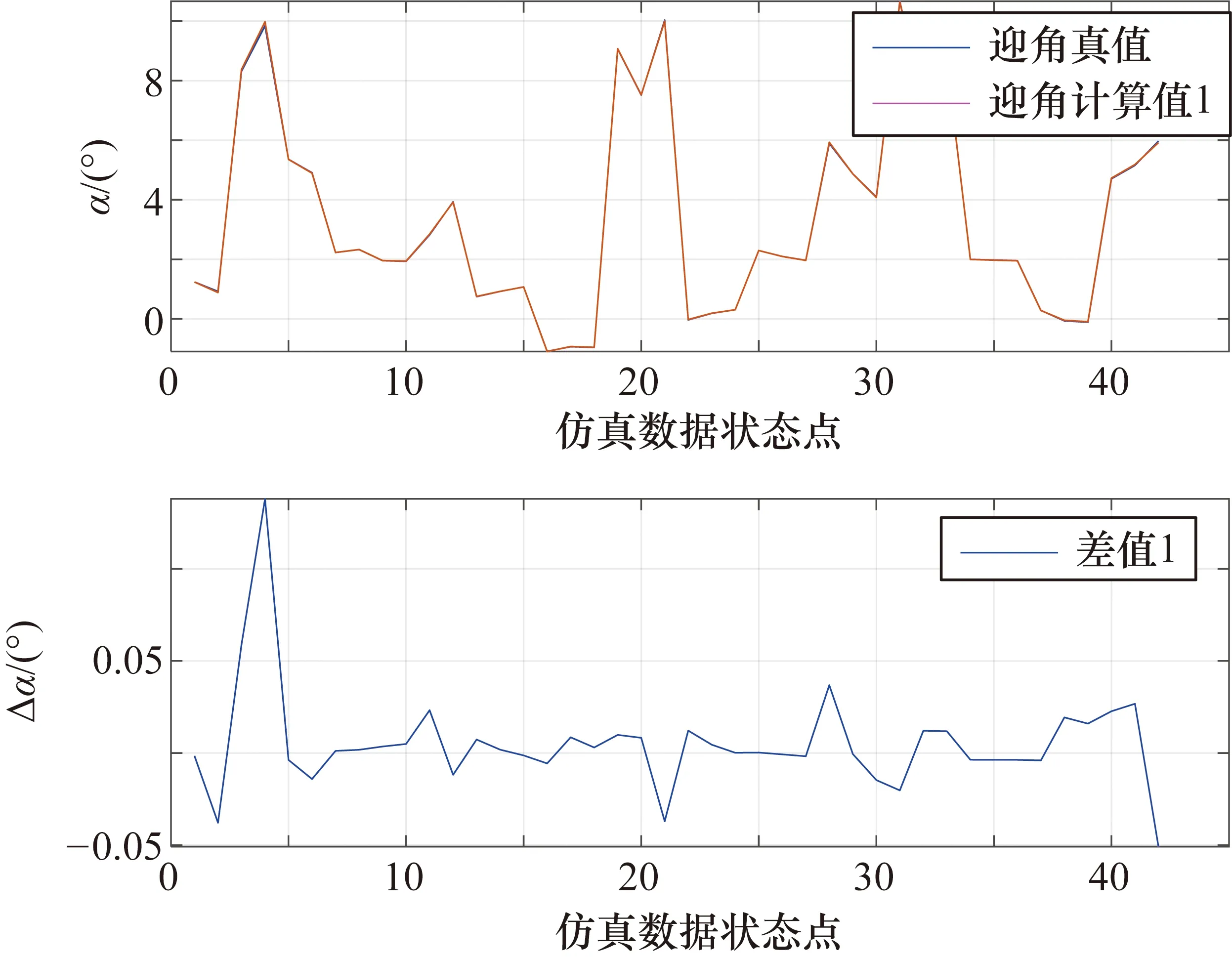
圖12 故障檢測算法計算的迎角誤差

圖13 使用故障檢測系統(tǒng)和不使用故障檢測系統(tǒng)的側滑角計算結果對比

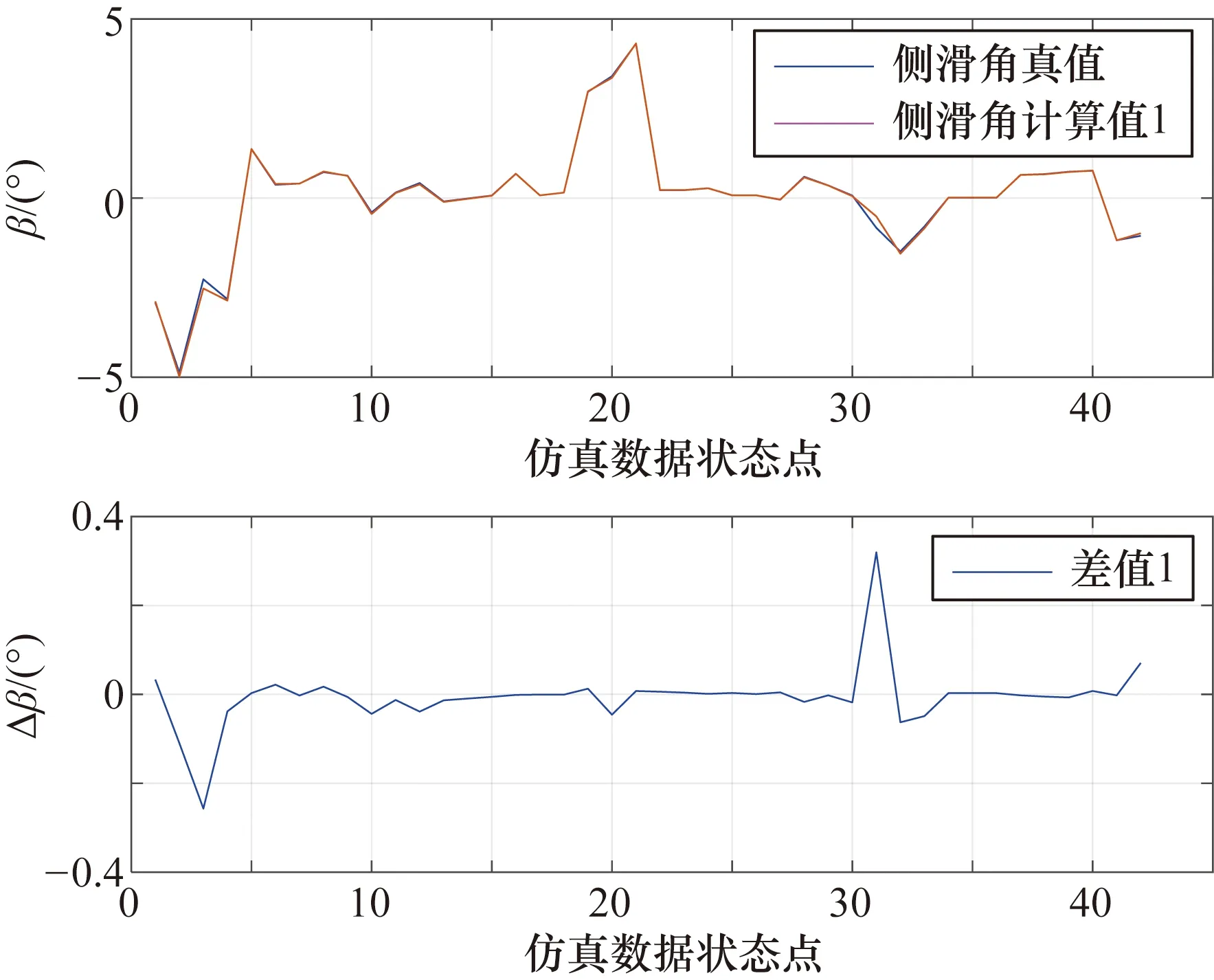
圖14 故障檢測算法計算的側滑角誤差

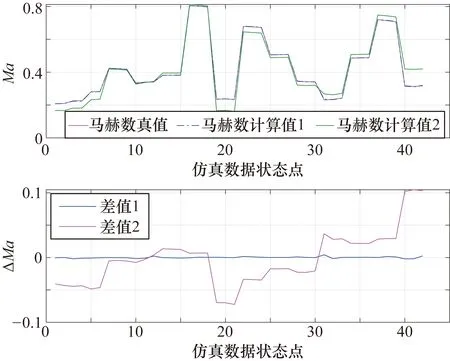
圖15 使用故障檢測系統(tǒng)和不使用故障檢測系統(tǒng)的馬赫數(shù)計算結果對比

圖13～圖18分別為是否使用開發(fā)的故障診斷算法計算側滑角、馬赫數(shù)以及靜壓的結果對比情況，圖中計算值1和差值1均為采用故障診斷算法得到的結果，計算值2和差值2均為未采用任何故障診斷算法直接計算得到的結果。從圖13～圖18中可以看出，采用了故障診斷算法的側滑角、馬赫數(shù)和靜壓的計算結果均精度較高，側滑角誤差在±0.35°以內(nèi)，馬赫數(shù)誤差在±0.004以內(nèi)，靜壓誤差在±40 Pa以內(nèi)；而未采用故障檢測算法的各大氣數(shù)據(jù)計算結果誤差很大。

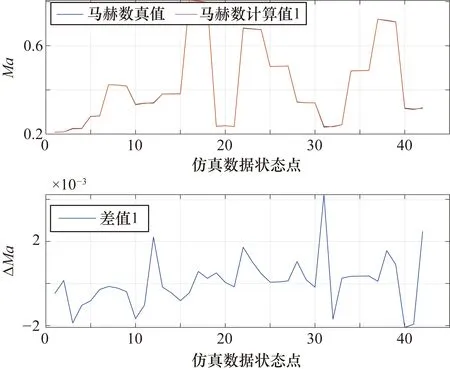
圖16 故障檢測算法計算的馬赫數(shù)誤差

圖17 使用故障檢測系統(tǒng)和不使用故障檢測系統(tǒng)的靜壓計算結果對比

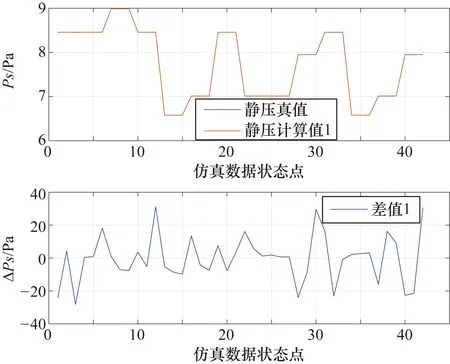
圖18 故障檢測算法計算的靜壓誤差

5 結束語

將機器學習算法應用于FADS系統(tǒng)算法中，采用隨機森林算法實現(xiàn)了故障傳感器的檢測，開發(fā)了以迎角和馬赫數(shù)為分段依據(jù)的FADS系統(tǒng)神經(jīng)網(wǎng)絡算法，采用飛行曲線數(shù)據(jù)對其進行測試。結果表明該算法能夠快速準確地計算出各大氣參數(shù)：迎角誤差小于±0.2°；側滑角誤差小于±0.3°；馬赫數(shù)絕對誤差小于±0.0105，相對誤差小于±1.1%；靜壓絕對誤差小于±300 Pa，相對誤差小于±0.35%。當出現(xiàn)單個故障測壓點時，設計的基于隨機森林分類器的故障診斷模塊能準確識別故障測壓點，采用的飛行曲線測試中測試準確率達到100%。在算法自動排除故障測壓點后，通過剩余的測壓點仍能快速準確地計算出大氣數(shù)據(jù)，此時迎角精度可達±0.2°，側滑角精度可達±0.35°，馬赫數(shù)誤差在±0.004以內(nèi)，靜壓誤差在±40 Pa以內(nèi)，依舊滿足嵌入式大氣數(shù)據(jù)系統(tǒng)的使用精度要求，從而實現(xiàn)了嵌入式大氣數(shù)據(jù)系統(tǒng)的故障診斷與容錯功能。