基于I/F起動和擴(kuò)展卡爾曼濾波的永磁同步電機(jī)全速域無傳感器控制方法*

趙毅恒, 寧博文, 盧少武, 劉 江

(武漢科技大學(xué) 冶金自動化與檢測技術(shù)教育部工程研究中心，湖北 武漢 430080)

0 引 言

永磁同步電機(jī)(PMSM)以其結(jié)構(gòu)簡單、體積小、重量輕、效率高的特點(diǎn)，廣泛應(yīng)用于各種領(lǐng)域。隨著永磁材料技術(shù)的不斷提高，對PMSM的研究也不斷成熟，電機(jī)性能不斷提高。PMSM的控制需要檢測轉(zhuǎn)子的位置，一般是通過在電機(jī)軸上安裝速度傳感器來獲取轉(zhuǎn)子位置和速度信息。由于速度傳感器受工業(yè)環(huán)境的限制和生產(chǎn)成本的影響，采用無速度傳感器控制已經(jīng)成了當(dāng)下研究的熱點(diǎn)[1]。

當(dāng)前常見的無傳感器控制算法有傳統(tǒng)滑模觀測器算法[2-3]、模型參考自適應(yīng)算法[4]、擴(kuò)展卡爾曼濾波器(EKF)算法[5-6]等。卡爾曼濾波器是在線性最小方差估計基礎(chǔ)上發(fā)展起來的一種遞推算法，在系統(tǒng)噪聲和測量噪聲均存在的情況下依然能保持系統(tǒng)的準(zhǔn)確觀測。EKF算法則是卡爾曼濾波算法在非線性系統(tǒng)的擴(kuò)展應(yīng)用，適合電機(jī)中高速范圍內(nèi)的速度估計。

電機(jī)運(yùn)行在零速和低速時，有用的信噪比較低，導(dǎo)致EKF算法在電機(jī)起動時對轉(zhuǎn)子位置和速度的檢測會失效。在需求量龐大的家電領(lǐng)域，例如洗衣機(jī)、空調(diào)這類對電機(jī)低速起動沒有嚴(yán)格限制，但對高速調(diào)速性能有一定要求的場合，可以采用恒電流頻率比(I/F)進(jìn)行電機(jī)低速的起動。I/F起動策略是一種電流閉環(huán)、轉(zhuǎn)速開環(huán)的控制，通過在原有的同步坐標(biāo)系中給定一個新的電流旋轉(zhuǎn)矢量，使給定的電流矢量恒加速旋轉(zhuǎn)至指定速度，帶動電機(jī)的轉(zhuǎn)子旋轉(zhuǎn)，到達(dá)指定速度后電機(jī)的轉(zhuǎn)速圍繞給定轉(zhuǎn)速波動并逐漸收斂至給定值，以完成I/F起動過程[7-8]。

由于I/F起動給定的角度和EKF估計的角度存在角度差，直接進(jìn)行兩種狀態(tài)的切換會使電機(jī)轉(zhuǎn)矩產(chǎn)生較大的波動，影響系統(tǒng)穩(wěn)定[9]。為此，本文通過設(shè)計反饋調(diào)節(jié)器，以該角度差作為反饋輸入以達(dá)到減小切換過程中給定電流和角度差的目的，同時避免切換過程中電流減小帶來的角度差的波動，保證切換的順利進(jìn)行，并通過仿真驗(yàn)證該方法的可行性和有效性。

1 PMSM數(shù)學(xué)模型

本文采用表貼式PMSM設(shè)計無速度傳感器控制算法，表貼式PMSM在三相靜止坐標(biāo)系α-β下的數(shù)學(xué)模型為

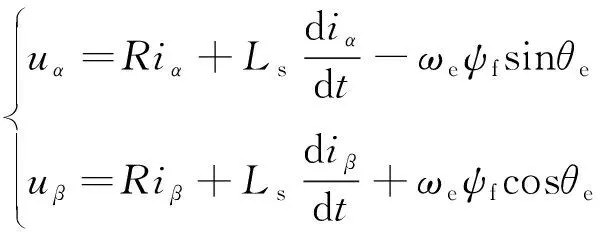
(1)

式中:uα、uβ、iα、iβ分別為電機(jī)兩相靜止坐標(biāo)系α、β軸下的電壓和電流；R、Ls、ψf分別為定子電阻、定子電感和永磁體磁鏈；ωe、θe為分別為電機(jī)的電角速度和轉(zhuǎn)子電角位置。

將式(1)變換為電流方程可得：

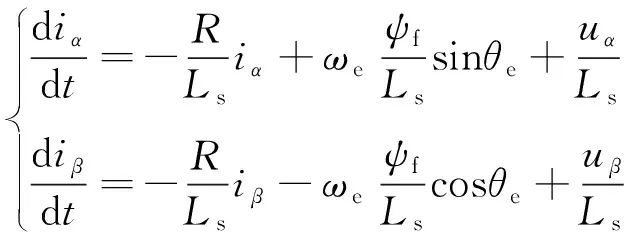
(2)

選取iα、iβ、ωe、θe作為狀態(tài)變量，考慮到電機(jī)的機(jī)械響應(yīng)遠(yuǎn)慢于電氣響應(yīng)，在較小的采樣周期內(nèi)轉(zhuǎn)速可以認(rèn)為近似不變，可以得到

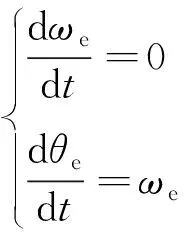
(3)

進(jìn)一步可以得到狀態(tài)空間方程為

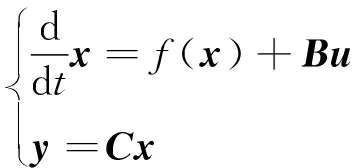
(4)

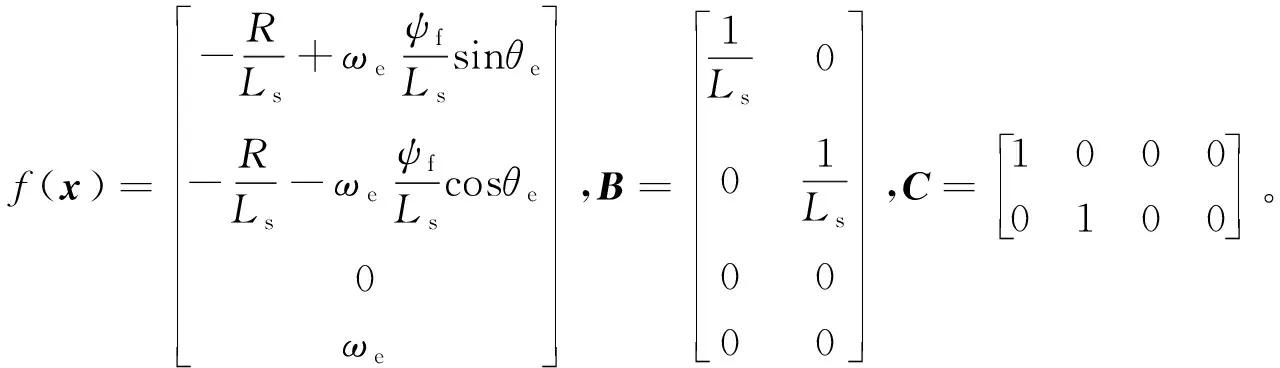
為構(gòu)建EKF，將狀態(tài)空間方程(4)離散化得到:

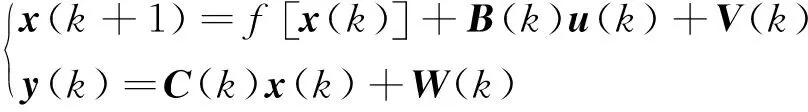
(5)

式中:V(k)為系統(tǒng)噪聲；W(k)為測量噪聲。

2 EKF

本文應(yīng)用EKF觀測電機(jī)速度和轉(zhuǎn)子位置，實(shí)現(xiàn)電機(jī)中高速運(yùn)行階段的無傳感器閉環(huán)控制。EKF是卡爾曼濾波器在非線性系統(tǒng)的應(yīng)用，通過將非線性系統(tǒng)進(jìn)行局部線性化，再進(jìn)行跟蹤，實(shí)現(xiàn)對目標(biāo)狀態(tài)最優(yōu)估計。EKF的狀態(tài)估計大致分為兩個階段，第一階段是預(yù)測階段，第二個階段是校正階段[10]，具體分為以下六個步驟：

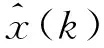
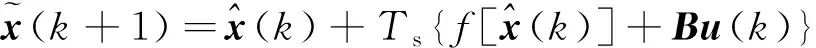
(6)

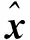
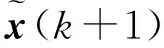
(7)

(3) 計算協(xié)方差矩陣:

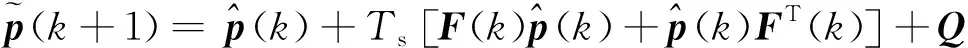
(8)

式中：F(k)為雅可比矩陣；Q為系統(tǒng)噪聲V的協(xié)方差矩陣。

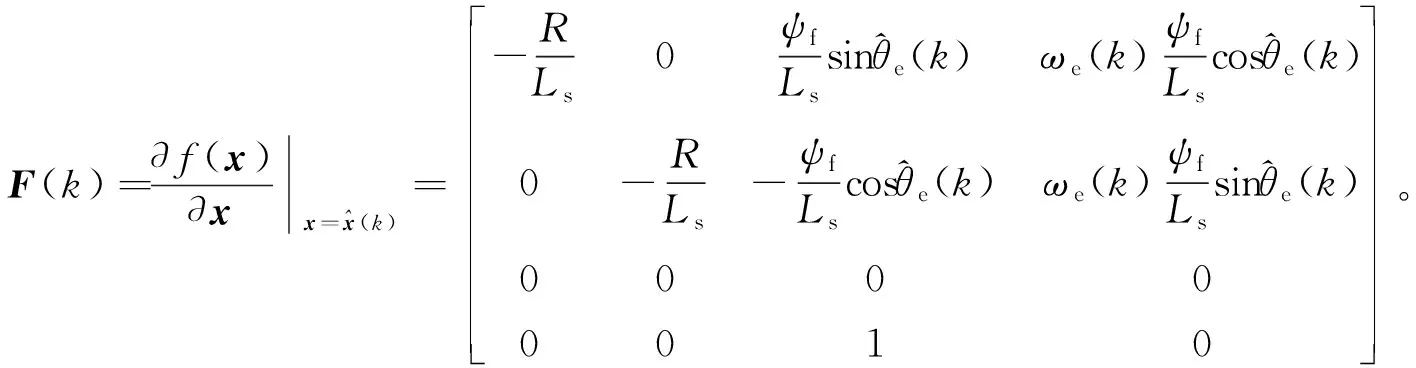
(4) 計算增益矩陣：

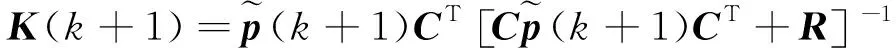
(9)

式中:R為測量噪聲W的協(xié)方差陣。

(5) 狀態(tài)矢量估計：

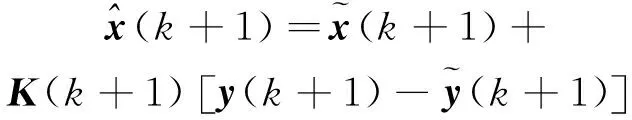
(10)

(6) 計算估計誤差協(xié)方差矩陣:

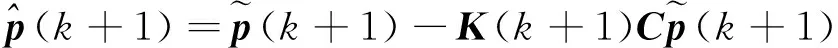
(11)

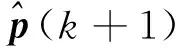
由于系統(tǒng)的干擾噪聲和測量噪聲是隨機(jī)的，實(shí)際運(yùn)用中對于系統(tǒng)和測量噪聲的協(xié)方差矩陣一般通過經(jīng)驗(yàn)和仿真確定，選擇的數(shù)值對算法的收斂性及估計精度有很大的影響，本文通過仿真調(diào)試后選擇給定參數(shù)為

(12)

3 基于轉(zhuǎn)矩電流自平衡的無傳感器起動過渡控制策略

3.1 I/F起動策略

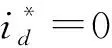
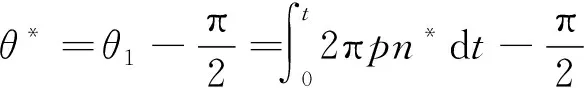
(13)

PMSM轉(zhuǎn)矩方程為

Te=1.5pIsψfsinδ

(14)

運(yùn)動方程為

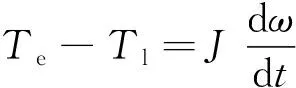
(15)

式中:δ為電機(jī)的功角,δ=θ1-θ2;速度n*=at;p為磁極對數(shù);a為電機(jī)起動加速斜率;Is為定子電流，當(dāng)Te-Tl=0時刻，電角度為θl。

電機(jī)起動時，隨著δ角度不斷增大，電機(jī)轉(zhuǎn)矩增大，當(dāng)δ大于θl時，電機(jī)開始加速，當(dāng)δ小于θl時，電機(jī)減速。這種“轉(zhuǎn)矩-功角自平衡性能”，使得電機(jī)起動時圍繞給定速度加速運(yùn)動，當(dāng)給定的速度過大,超過最大起動速度時電機(jī)會失步。由于給定加速度的突變會導(dǎo)致超調(diào)，加速過程采用變加速的方式起動，在給定速度加上一階慣性環(huán)節(jié)：

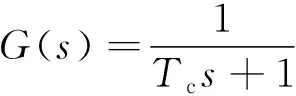
(16)

式中：Tc為慣性環(huán)節(jié)時間常數(shù)。

慣性環(huán)節(jié)使得給定速度平滑地達(dá)到指定速度，可以有效減少電機(jī)達(dá)到指定速度時的超調(diào)。圖1是電機(jī)開始起動時刻，即Te=Tl時電流矢量圖。

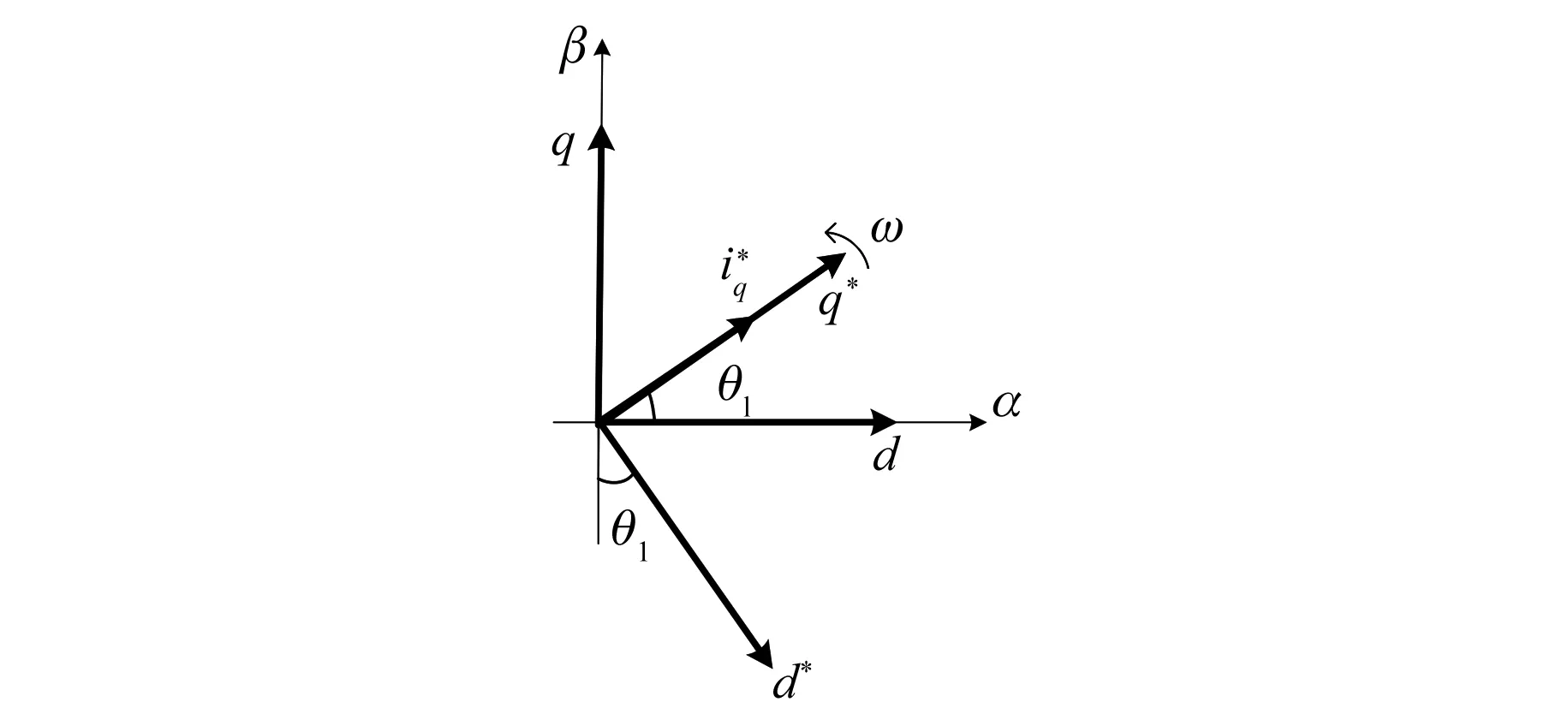
圖1 電機(jī)起動時電流矢量圖

3.2 轉(zhuǎn)矩電流自平衡切換策略分析

I/F控制采用的是速度環(huán)開環(huán)、電流環(huán)閉環(huán)的控制方式，EKF控制是電流速度雙閉環(huán)控制。在兩種控制方法切換時，I/F起動位置角的給定θ*需要切換為EKF估計的位置角θekf，兩者相差的電角度為

θerr=θekf-θ*

(17)

根據(jù)轉(zhuǎn)矩公式(14)可知強(qiáng)行切換電流和角度時，角度的突變會導(dǎo)致電流和轉(zhuǎn)矩有很大的脈動。所以在切換的過程中，需要減小q軸電流，使切換前后電流接近，并使I/F起動給定的電流矢量在實(shí)際的q軸上的電流分量盡可能的大[12]。

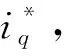
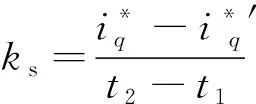
(18)

在常規(guī)方法中ks的取值越大，切換時間越短，轉(zhuǎn)速波動隨之變大。在給定電流減小到一定值后切換到閉環(huán)控制，此過程由于電機(jī)到達(dá)切換轉(zhuǎn)速時，閉環(huán)后實(shí)際的q軸電流未知，如果電流過小可能會導(dǎo)致電機(jī)出現(xiàn)失步，故減小的電流值不能設(shè)定的過小。同時當(dāng)電流減小后直接切換到速度閉環(huán)控制，會導(dǎo)致轉(zhuǎn)矩突變，對電機(jī)的穩(wěn)定運(yùn)行十分不利，若再緩慢減小角度誤差，會使過渡時間太長，不利于實(shí)際運(yùn)行。

為此本文提出一種改進(jìn)方法，考慮到切換電流和兩者輸入角度差的關(guān)系，在I/F控制起動達(dá)到勻速階段后，電機(jī)負(fù)載不變時，根據(jù)“轉(zhuǎn)矩-功角自平衡”，由式(14)可知在一定范圍內(nèi)控制電流和功角δ的關(guān)系成負(fù)相關(guān)且兩種切換前后的角度差為

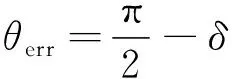
(19)

因此，可以通過對θerr反饋調(diào)節(jié)來減少給定電流的大小，并使得θerr減小，達(dá)到同時減小給定電流和θerr，最終收斂到id=0控制點(diǎn)的目的。圖2是過渡過程中給定電流所在的給定軸旋轉(zhuǎn)的角度θ1帶動電機(jī)轉(zhuǎn)子實(shí)際轉(zhuǎn)過的電角度θ2時的矢量圖。電機(jī)無傳感器控制中實(shí)際的位置角θ2由EKF估計的位置角θekf得到。

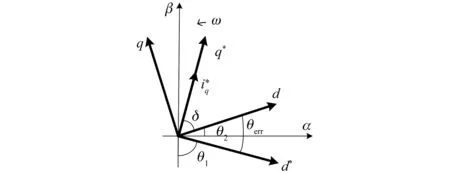
圖2 過渡過程電流矢量和實(shí)際轉(zhuǎn)子位置示意圖

對于表貼式PMSM，轉(zhuǎn)矩的極值通過對式(14)求導(dǎo)，可得電機(jī)的最佳控制點(diǎn)為

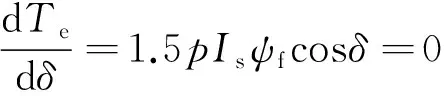
(20)

求得此時位置角度差

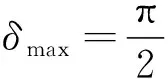
(21)

θerr min=0

(22)

由于電機(jī)切換過程中轉(zhuǎn)速基本保持不變，可以認(rèn)為Te=Tl，且為常值，即:

Te=1.5pIsψfsinδ=1.5pIsψfcosθerr

(23)

在id=0的I/F起動矢量控制方式下，Is等于q軸上的電流Iq,可以得出電流Iq與θerr的關(guān)系：

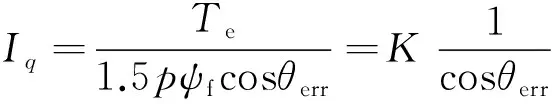
(24)

由上述分析可以得到不同的負(fù)載情況下Iq-θerr的工作曲線如圖3所示。

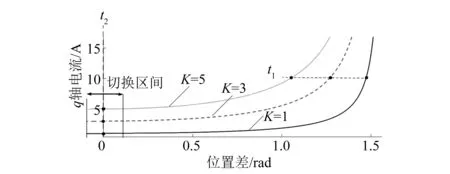
圖3 q軸電流和位置角度差工作曲線

圖3中t1為切換前過渡過程的開始時刻，此時逐漸減小電流，t2為工作曲線第一次運(yùn)行到θerr=0的時刻。過渡過程中隨著電流的減小，電流變化對θerr的影響逐漸增大，到達(dá)t2時刻后工作曲線會在θerr=0工作點(diǎn)附近來回運(yùn)動，此時若不及時的切換到速度電流雙閉環(huán)控制，電流很小的波動會引起θerr的振蕩，甚至發(fā)散。

針對這一問題，通過對反饋調(diào)節(jié)進(jìn)行改進(jìn)，在θerr較大時加大電流反饋調(diào)節(jié)的作用，在θerr靠近0時減小調(diào)節(jié)作用。根據(jù)這一特點(diǎn)，在PI調(diào)節(jié)器前增加一個調(diào)節(jié)器，設(shè)定調(diào)節(jié)器倍率系數(shù)為

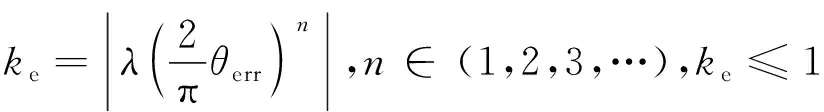
(25)

n的值越大，對于上述調(diào)節(jié)作用越明顯，λ的取值決定調(diào)節(jié)器的作用范圍。整個負(fù)反饋調(diào)節(jié)過程為

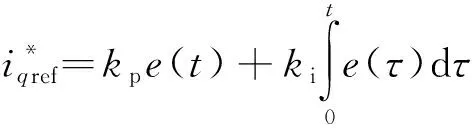
(26)

e(t)=keθerr

(27)

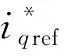
圖4為反饋調(diào)節(jié)器框圖，圖5為增加調(diào)節(jié)器后的不同的負(fù)載情況下Iq-θerr的工作曲線。

圖4 反饋調(diào)節(jié)器框圖

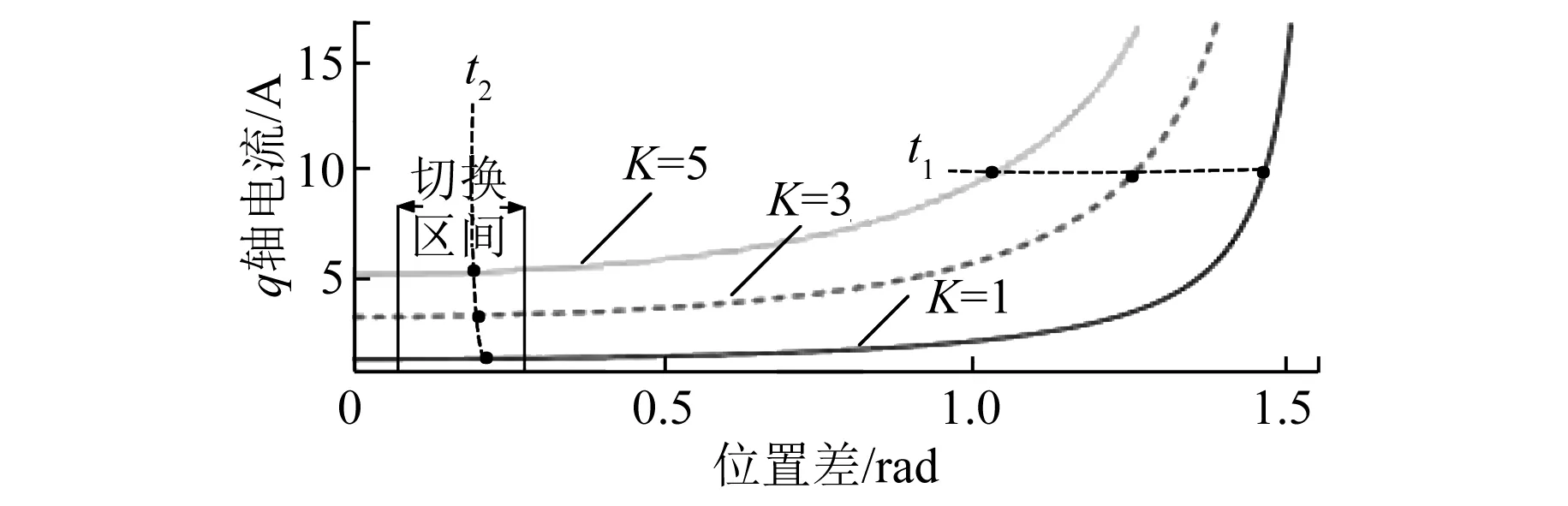
圖5 加調(diào)節(jié)器后q軸電流和位置角度差工作曲線

從圖5中可以看出，此方法改變了Iq-θerr曲線上的工作范圍，在θerr減小到一定值時會迅速減少反饋調(diào)節(jié)器的輸出，使得t2時刻新的平衡點(diǎn)靠近而不達(dá)到θerr=0，并保持q軸電流和θerr穩(wěn)定的狀態(tài)，避免了因θerr的極性變化造成θerr發(fā)散而導(dǎo)致切換失敗的情況。根據(jù)新的工作范圍，在切換前q軸電流和θerr減小到了一定值且基本保持不變，轉(zhuǎn)矩趨于穩(wěn)定，同時保證了切換前后的電流相匹配。在無調(diào)節(jié)器和有調(diào)節(jié)器情況下，切換前過渡過程q軸電流的對比示意圖如圖6所示。

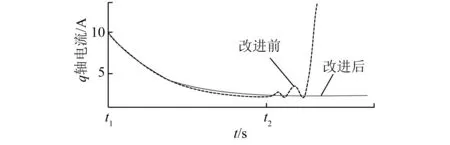
圖6 切換前過渡過程q軸電流對比示意圖

4 仿真分析

為驗(yàn)證本文提出方法的有效性，在MATLAB/Simulink中搭建基于I/F起動和EKF相結(jié)合的PMSM無速度傳感器控制系統(tǒng)模型，整個仿真系統(tǒng)框圖如圖7所示。

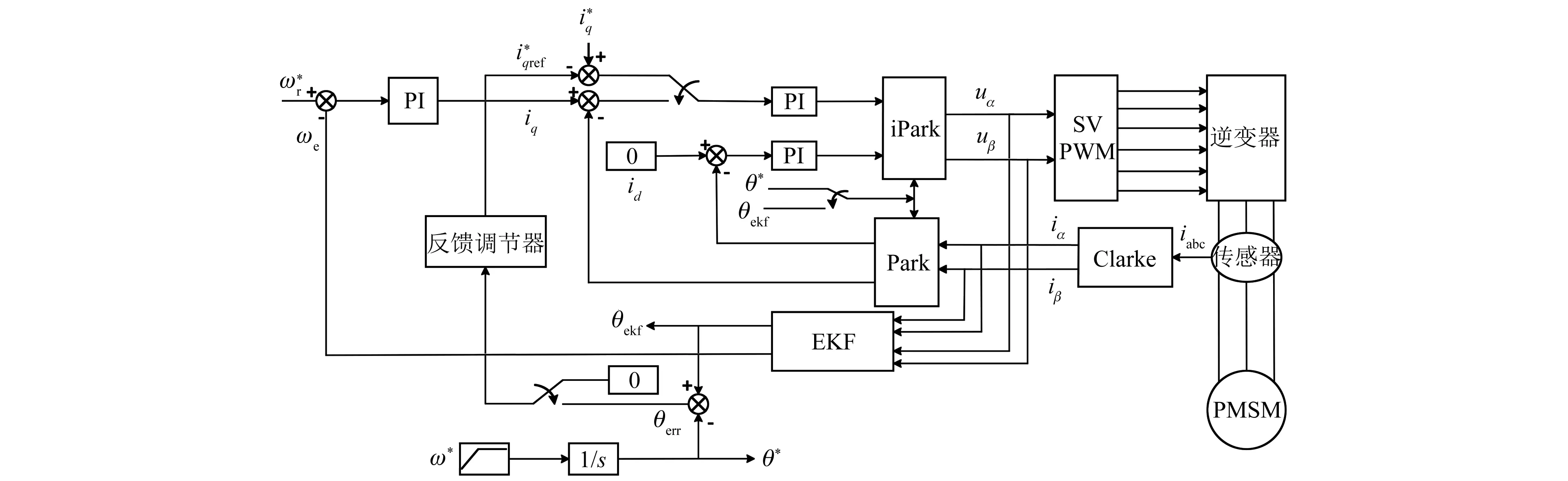
圖7 PMSM無速度傳感器控制系統(tǒng)框圖

中PMSM參數(shù)設(shè)定為,極對數(shù)Pn=4，定子電感Ls=8.5 mH，定子電阻Rs=2.875 Ω，磁鏈Ψf=0.175 Wb，轉(zhuǎn)動慣量J=0.01 kg·m2，阻尼系數(shù)B=0.008 N·m·s。I/F起動給定的加速斜率為a=125.6 rad/s2，初始給定電流為10 A，角度差反饋環(huán)節(jié)調(diào)節(jié)器參數(shù)取n=3、λ=2，EKF輸入為電機(jī)在靜止坐標(biāo)系下的定子電壓和定子電流，輸出為轉(zhuǎn)速和轉(zhuǎn)子估計位置。圖8是電機(jī)空載和負(fù)載Tl=2 N·m時完整運(yùn)行過程的速度變化情況，I/F起動速度在1 s后達(dá)到600 r/min，進(jìn)入切換狀態(tài)，在2.5 s后進(jìn)入電流速度雙閉環(huán)控制，在3 s給定1 000 r/min，4 s給定800 r/min。

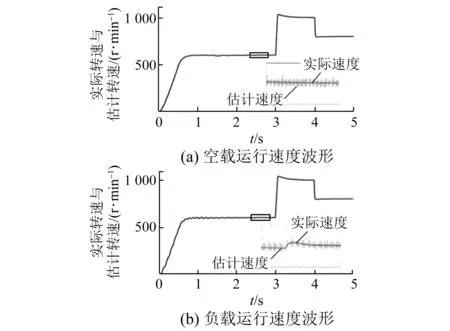
圖8 無速度傳感器控制系統(tǒng)速度響應(yīng)波形

圖9是在上述負(fù)載Tl=2 N·m情況下整個過程q軸電流的變化，圖10是電機(jī)切換過程中I/F給定位置、EKF觀測位置和實(shí)際位置。圖11是切換狀態(tài)中的θerr的變化。可以看出，在反饋調(diào)節(jié)器的作用下，位置角度差隨著電流的減小自動減小，在θerr靠近0前趨于穩(wěn)定，切換前后電流基本保持一致。

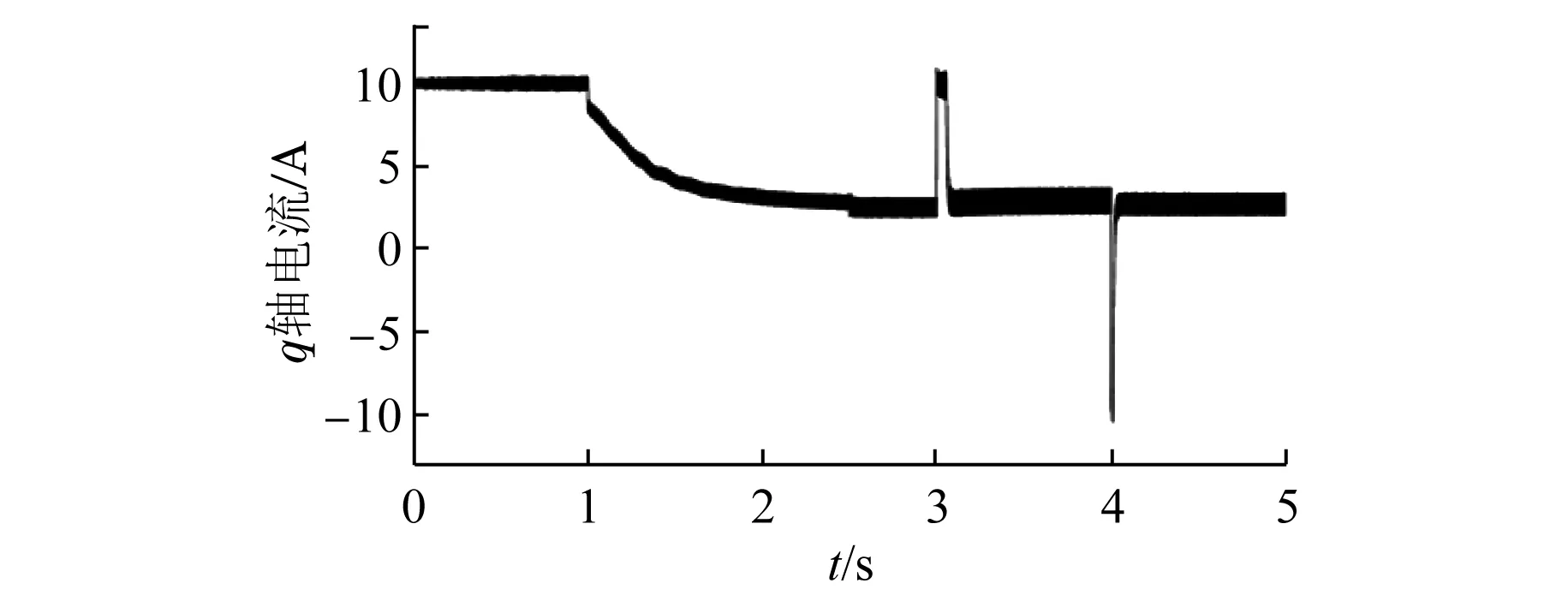
圖9 起動和加速減速全過程q軸電流

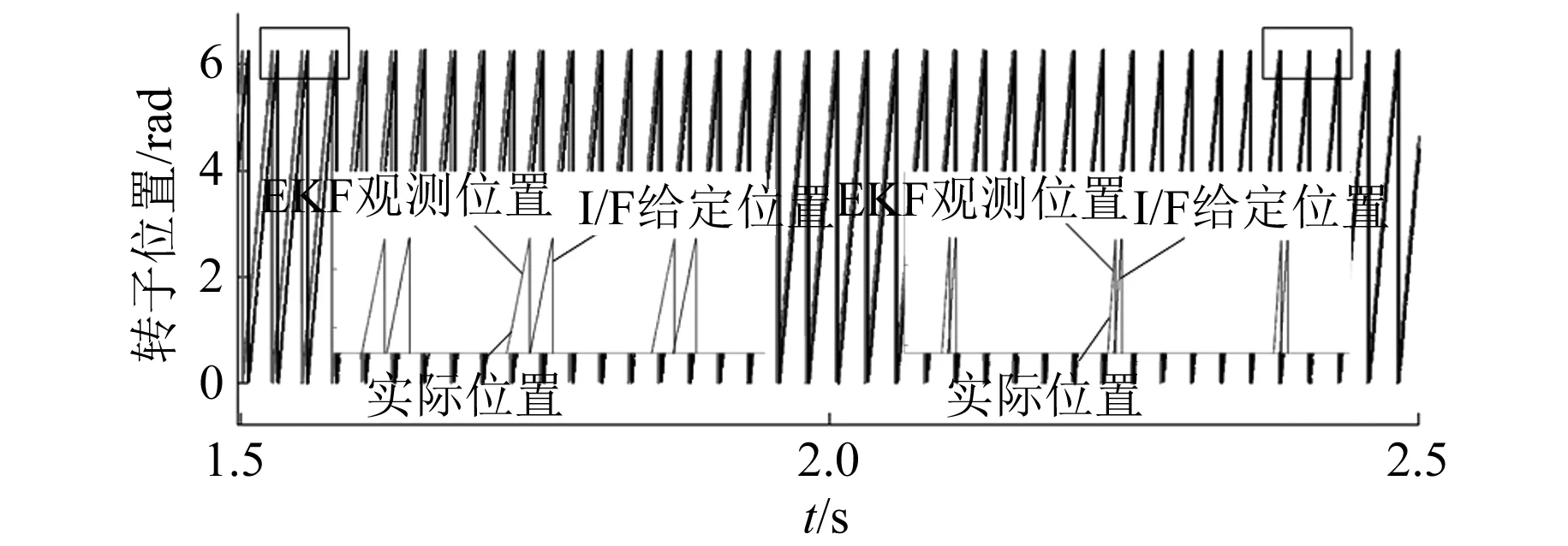
圖10 切換狀態(tài)中I/F給定位置、EKF觀測位置和實(shí)際位置

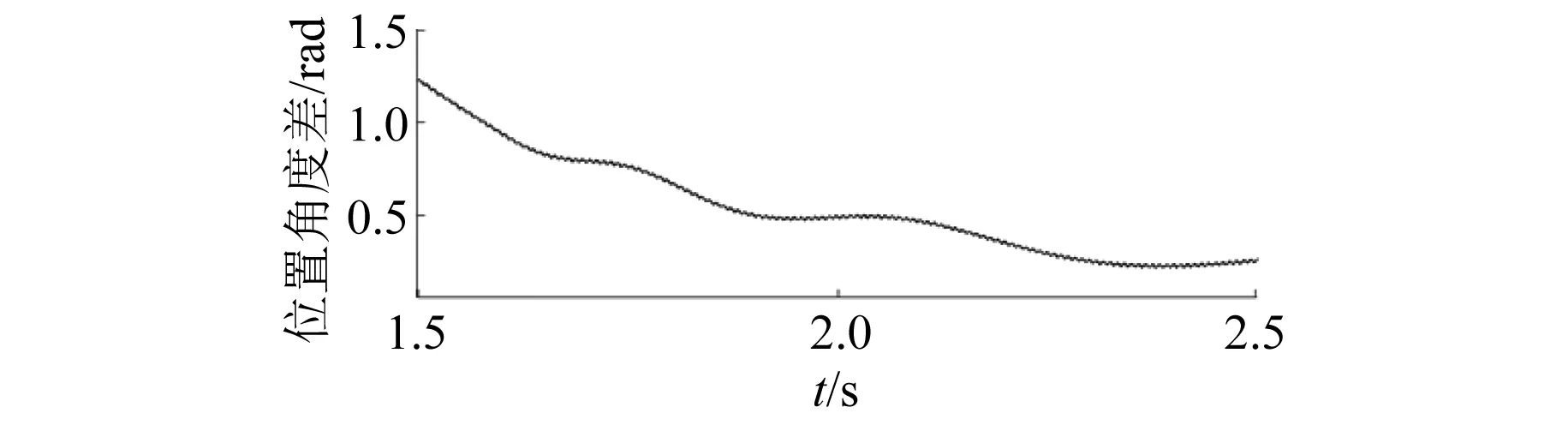
圖11 切換狀態(tài)中位置角度差θerr

圖12是空載條件下按不同的比例k取值均勻減小電流的常規(guī)切換方法和本文改進(jìn)切換方法的對比。當(dāng)k取100時電流下降較快，當(dāng)k取10時電流下降較慢，常規(guī)方法給定的切換電流大小減小為5 A。圖13是電機(jī)帶負(fù)載Tl=2 N·m起動時常規(guī)切換和本文改進(jìn)方法的起動對比圖，從圖12、圖13中可以看出，常規(guī)方法在切換前后電流變化較大，導(dǎo)致轉(zhuǎn)速產(chǎn)生波動，而改進(jìn)的切換方法在切換前后電流基本相等，轉(zhuǎn)速波動小。

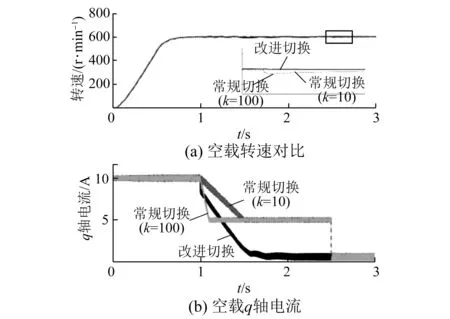
圖12 空載起動至切換過程常規(guī)和改進(jìn)方法電流轉(zhuǎn)速對比圖

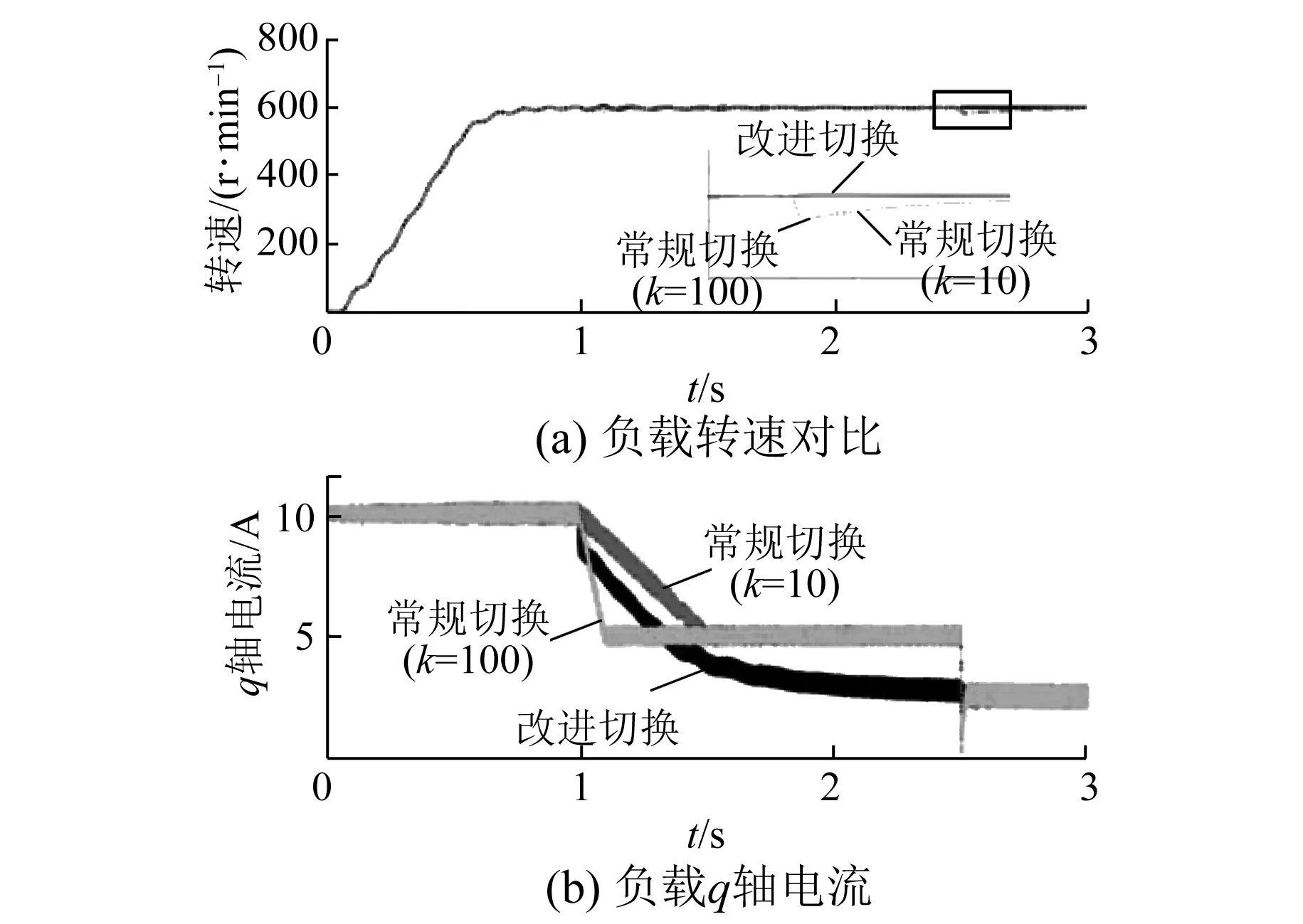
圖13 負(fù)載起動至切換過程常規(guī)和改進(jìn)方法電流轉(zhuǎn)速對比圖

圖14為負(fù)載Tl=6 N·m時，常規(guī)方法中給定電流減小為5 A時的起動速度曲線，可以看出在給定較大負(fù)載情況下，由于給定電流過小，此時常規(guī)方法電機(jī)起動失敗，而改進(jìn)方法則可以正常運(yùn)行。

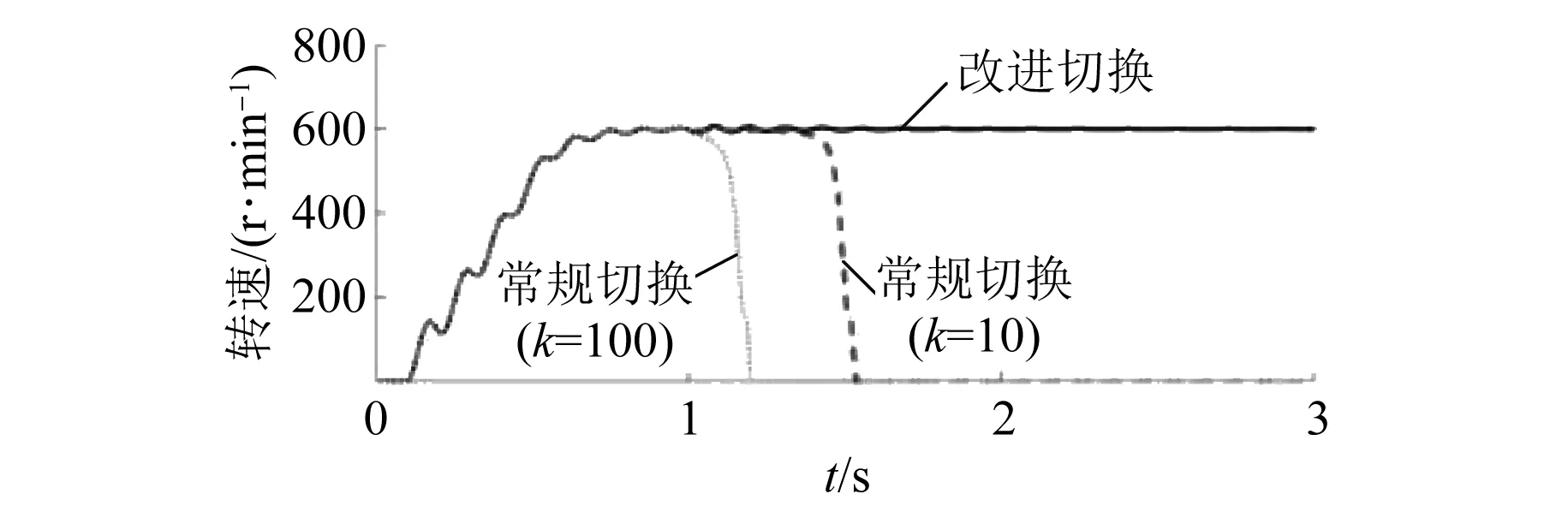
圖14 較大負(fù)載下起動轉(zhuǎn)速對比圖

從以上分析可以看出，本文提出的方法在切換前q軸電流減小到一定值后，同切換后EKF無傳感器閉環(huán)控制的q軸電流大小基本一致，切換后轉(zhuǎn)速保持穩(wěn)定，整個切換過程對于不同的負(fù)載具有較強(qiáng)的自適應(yīng)性和魯棒性，與常規(guī)切換方法相比，切換過程更穩(wěn)定。

5 結(jié) 語

本文針對PMSM全速域范圍無速度傳感器運(yùn)行問題，在零速和低速階段采用I/F起動，中高速切換為EKF閉環(huán)控制，并設(shè)計了一種合理的過渡方式來切換電流和位置。仿真結(jié)果表明，該方法可以實(shí)現(xiàn)PMSM全速范圍下的穩(wěn)定運(yùn)行，在低速時以電流閉環(huán)的方式起動，滿足各種負(fù)載的要求，中高速狀態(tài)下EKF能準(zhǔn)確估計電機(jī)的位置，所設(shè)計的切換方法保證了過渡過程的可靠性和平穩(wěn)性。