一種揭示異質無線傳感器網絡惡意程序傳播的動力學模型*

沈士根，楊淑敏，黃龍軍，劉建華*，吳國文，張 紅，曹奇英

(1.紹興文理學院計算機科學與工程系，浙江 紹興312000；2.東華大學計算機科學與技術學院，上海201620)

隨著異質無線傳感器網絡(Heterogeneous WSNs，HWSNs)的應用越來越廣泛，HWSNs 中惡意程序傳播導致的安全問題日益嚴峻[1-3]。 由于惡意程序可以根據代碼構成實現自我復制的功能，而且惡意程序一旦被激活就可以主動進行傳播，使得惡意程序將以指數增長方式四處擴散，嚴重威脅HWSNs 的數據安全和網絡可靠性[4-6]。

要研究HWSNs 惡意程序的傳播問題，首先需要通過建模分析HWSNs 惡意程序傳播模型，再進一步研究其穩定性，從而揭示HWSNs 惡意程序的傳播規律，為惡意程序的防御、傳播遏制以及HWSNs 性能安全的提高提供借鑒和參考。 王小明團隊[7]較早研究了WSNs 中的惡意程序傳播問題，在考慮節點死亡狀態基礎上擴展傳統的SIR 模型得到了iSIRS 傳播模型，系統研究了移動傳感網中的惡意程序傳播問題，建立了基于偏微分方程理論的惡意程序傳播時空動力學模型[8]、基于元胞自動機的傳播模型[9]以及SIRD 模型[10]，分析了動力學模型的穩定性和分歧性[11]，還很好地綜述了傳感器網絡惡意程序傳播模型和遏制方法[12]。 羅小娟等人[13]融合免疫機制，得到了一種改進的SIR 模型。 黃一才等人[14]綜合考慮節點通信距離、休眠和隔離狀態提出一種包含8 個狀態的惡意程序傳播模型。 Song 和Zhang[15]提出了具有時滯性質的e-SEIR 模型。 Nowzari 等人[16]以異質節點構成的有向圖為基礎，提出了一種SEIV(Susceptible-Exposed-Infected-Vigilant)模型。 Zhang 等人[17]提出了一種SAIS(Susceptible-Alert-Infectious-Susceptible)模型并評估了不同警報策略的作用。 Singh 等人[18]考慮WSNs 傳感節點通信半徑和節點分布密度，提出了一種考慮接種機制的SEIRV(Susceptible-Exposed-Infected-Recovered-Vaccinated)模型。 Acarali等人[19]以基于WSNs 的物聯網為基礎，建立了一種能綜合反映節點處理能力有限、能量有限和節點密度高等物聯網特性的IoT-SIS 模型。 Shen 等人[20]擴展傳統的SIR 模型從而得到一種反映節點異質特性的SIR 模型，并對模型的穩定性進行了分析。 Liu 等人[21]針對可充電WSNs，提出了一種考慮電源狀態的SILS(Susceptible-Infected-Low energy-Susceptible)模型。 其他典型的模型還有HSIORD(Heterogeneous Susceptible-Infected-isOlated-Removed-Deceased ) 模型[22]、 SITPS ( Susceptible-Infected-Traced-Patched-Susceptible)模型[23]、車聯網惡意程序隨機傳播模型[24]、考慮社會屬性的物聯網惡意程序傳播模型[25]、以及反映節點時滯特性[26-27]、空間關聯性[28]、干擾攻擊傳播[29]、攻防博弈[30]的WSNs 惡意程序傳播模型。 然而，上述相關文獻對WSNs 惡意程序傳播過程中節點狀態的表述還不全面，對惡意程序傳染率的表達沒有體現WSNs 的異質特性。

本文提出一種考慮節點潛伏和隔離狀態，同時反映節點異質特性的HWSNs 惡意程序傳播模型，再分析其穩定性，為揭示HWSNs 惡意程序擴散機制和系統管理員有效抑制HWSNs 惡意程序傳播提供理論指導。 首先，根據惡意程序可能潛伏和惡意節點可能被成功檢測后隔離的特性，提出一種HWSNs 惡意程序傳播模型SEQIRD(Susceptible-Exposed-Quarantined-Infected-Recovered-Dead)；其次，以與單個異質傳感器節點(Heterogeneous Sensor Node，HSN)直接通信的節點數，即節點的度，反映其異質特性，建立微分方程，從而反映HWSNs 惡意程序傳播過程中具有異質性的傳感器節點狀態的動態變化過程；然后，根據穩定點的數學特性，計算該模型的穩定點，采用下一代矩陣法計算該模型的基本再生數，并證明該模型無病穩定點的局部漸進穩定性。 表1 從模型優點、缺點、關鍵貢獻等方面對本文模型和現有模型進行了比較。

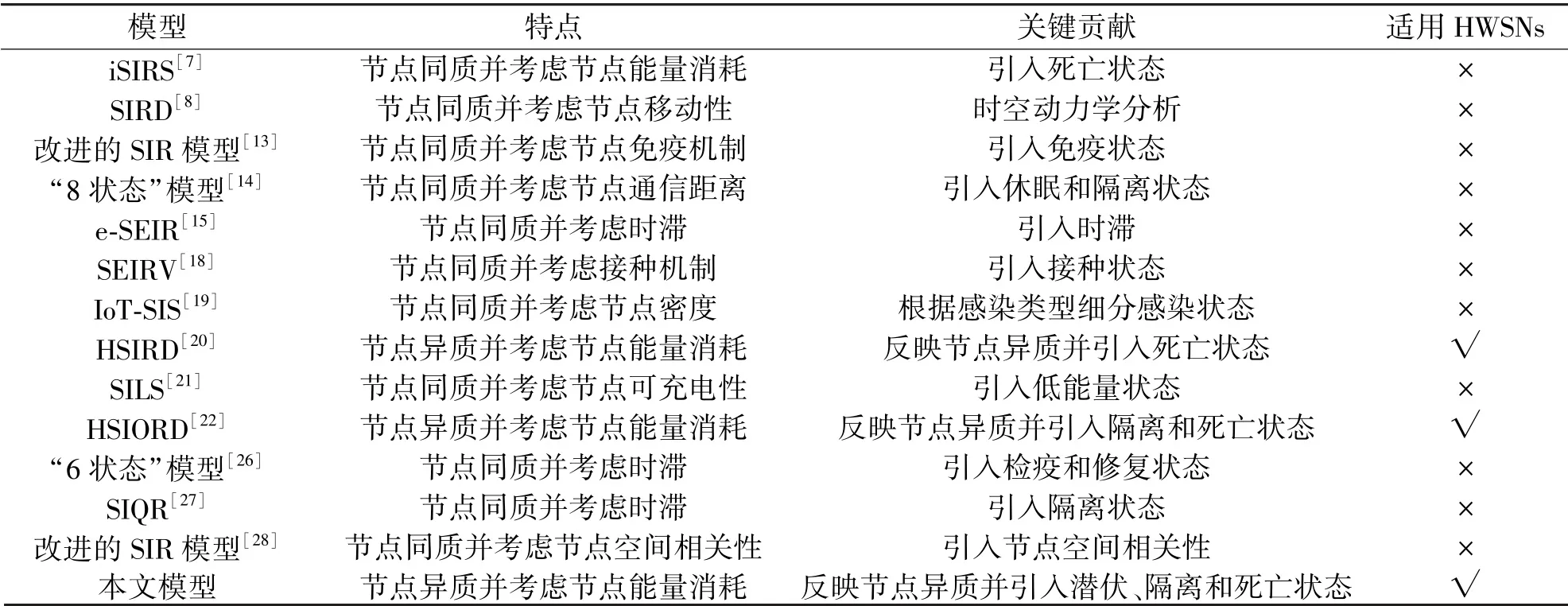
表1 本文模型和現有模型的比較

1 HWSNs 惡意程序傳播模型

HWSNs 中的HSN 在被惡意程序攻擊而感染前后狀態會發生一系列變化，本文共定義六種HSN 狀態:易感狀態S、潛伏狀態E、隔離狀態Q、感染狀態I、恢復狀態R、死亡狀態D，如圖1 所示。 當HSN 因為安全等級較低而存在漏洞，有被感染風險的時候，所處的狀態稱為易感狀態S；處于易感狀態的HSN 被惡意程序感染，但是惡意程序還沒有被激活的狀態稱為潛伏狀態E；當HSN 因存在惡意程序而被安全系統發現并隔離時所處的狀態稱為隔離狀態Q；被惡意程序感染的HSN 在與其他節點通信的過程中傳播惡意程序時所處的狀態稱為感染狀態I；當HSN 中的惡意程序被安全系統消除，以后不會再受該惡意程序攻擊時所處的狀態稱為恢復狀態R；HSN 因為環境影響和能量消耗等因素而不能提供正常服務時所處的狀態為死亡狀態D。

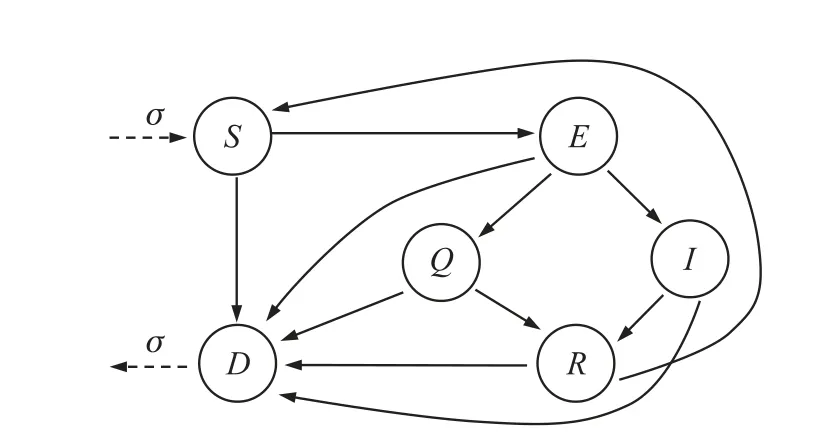
圖1 HWSNs 惡意程序傳播模型SEQIRD 中節點狀態轉換圖

設一個HWSNs 共包含M個HSN，與一個HSN通信的其他HSN 數量為i(1≤i＜M)個，即該HSN 的度為i。 記Si(t)、Ei(t)、Qi(t)、Ii(t)、Ri(t)、Di(t)表示度為i的HSN 在t時刻分別處于S、E、Q、I、R、D狀態的數量占傳感器節點總數的比例，則易得:

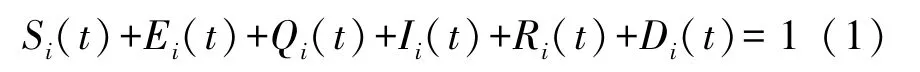
將處于感染狀態I且度為i的HSN 初始比例記為o，即

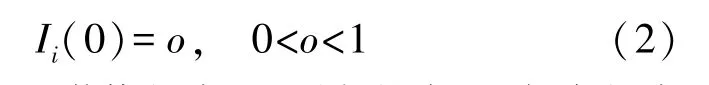
假設分別處于潛伏狀態E、隔離狀態Q、免疫狀態R和死亡狀態D且度為i的HSN 初始比例均為0，即

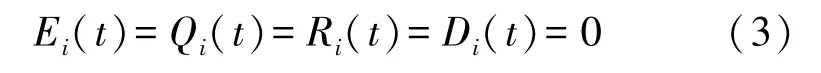
根據式(1)～式(3)，可以得到處于易感狀態S且度為i的HSN 初始比例:

在t時刻，處于感染狀態的HSN 向周圍度為i的易感狀態節點傳播惡意程序的概率記為Θi(t)，則

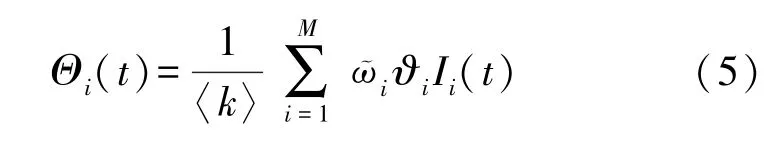
式中:HWSNs 的平均度為〈k〉，HSN 度為i的概率為?i，惡意程序被激活啟動后處于活躍狀態時向其他不存在惡意程序的HSN 發起攻擊的概率為?i。 而且，參數滿足條件:

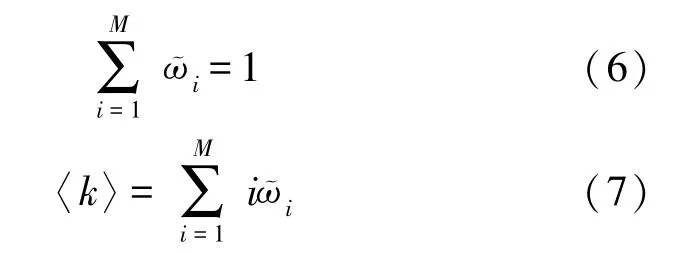
度為i的HSN 從狀態x(x∈{S，E，Q，I，R，D})轉換到狀態y(y∈{S，E，Q，I，R，D})的概率記為qxyi。另外，為了維持整個HWSNs 正常的生命周期，會有比例為σ的度為i且易感的HSN 新接入網絡，用于更換一些損壞的HSN 以保證整個HWSNs 正常運行。對處于狀態S的HSN，其比例變化值等于σ加上從狀態R轉換到S的比例，減去從狀態S轉換到狀態E的比例，再減去從狀態S轉換到狀態D的比例，用微分方程可以表示為:

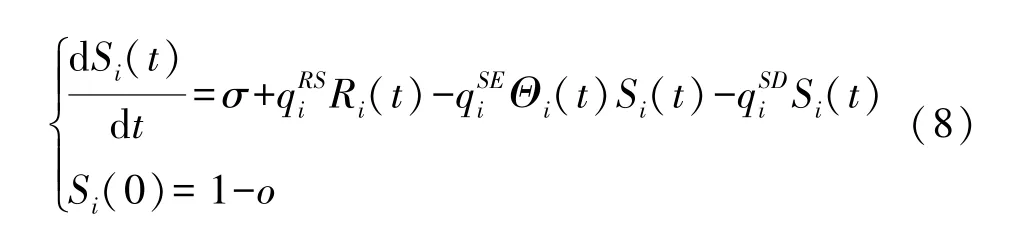
類似地，可以得到描述其他狀態比例變化的微分方程為:

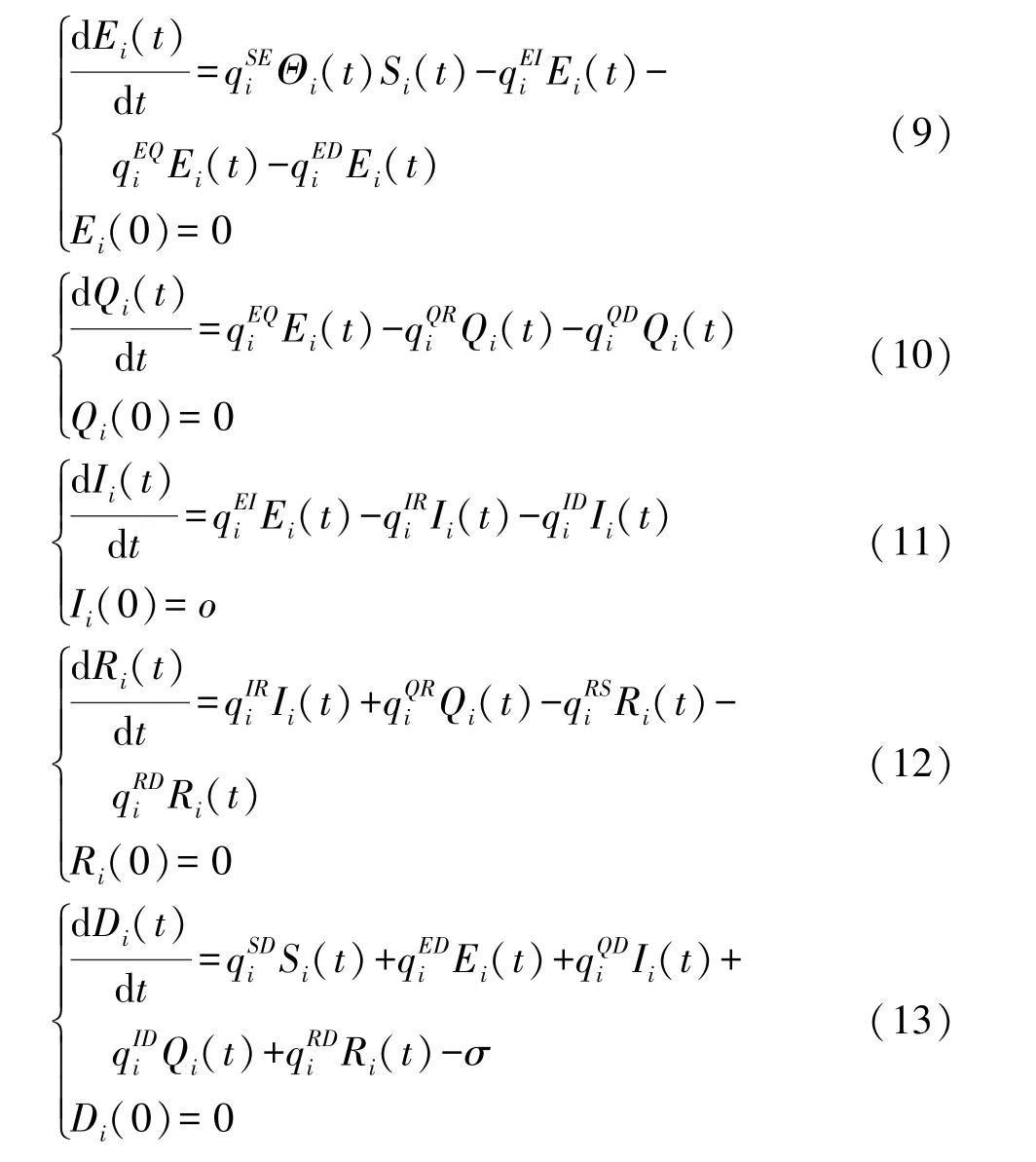
2 惡意程序傳播模型SEQIRD 的穩定點

通過計算得到模型SEQIRD 的穩定點，能夠確定HWSNs 中惡意程序消亡或傳播的閾值，從而能對面向惡意程序傳播的HWSNs 防御提供有效的指導。 實際上，求解模型SEQIRD 的穩定點跟求解微分方程組的穩定點一致，具體求解時，令反映各個狀態動態變化的微分方程值為0 后形成方程組，再求解該方程組即可得到模型SEQIRD 的穩定點。

定理1面向惡意程序傳播的模型SEQIRD 存在穩定點。

證明當模型SEQIRD 中反映各節點狀態動態變化的微分方程達到穩定點時，各節點狀態動態變化值均為0，即:

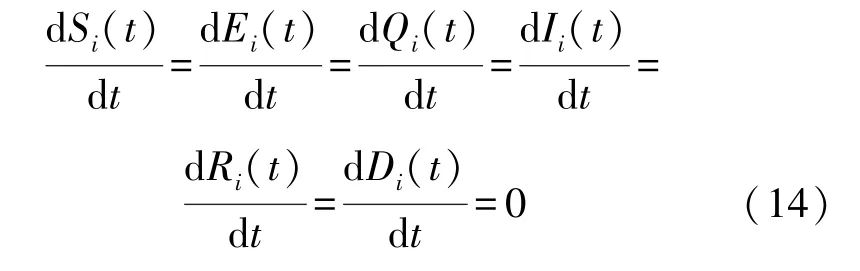
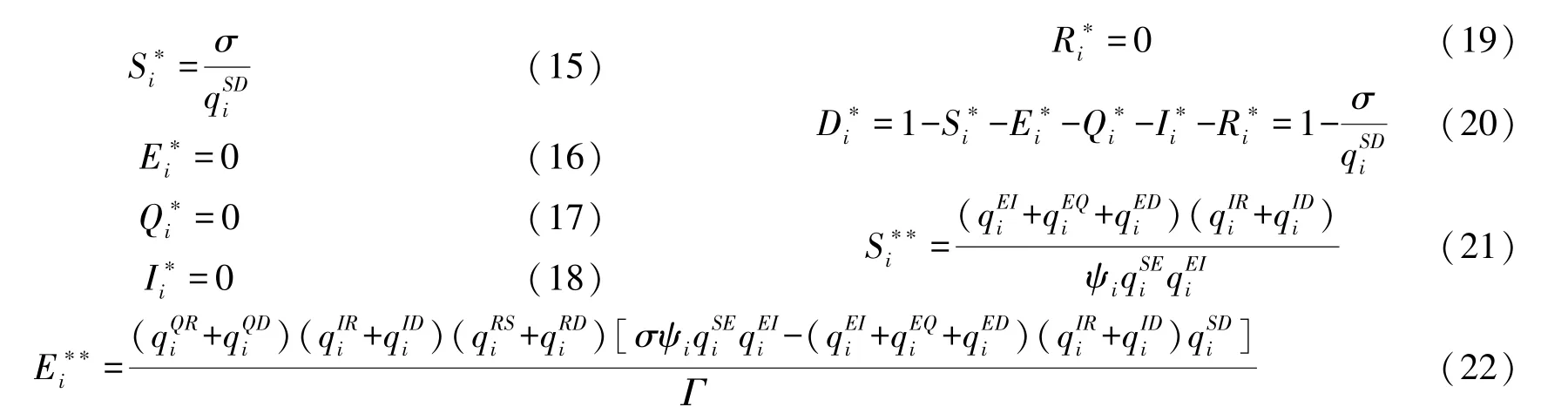
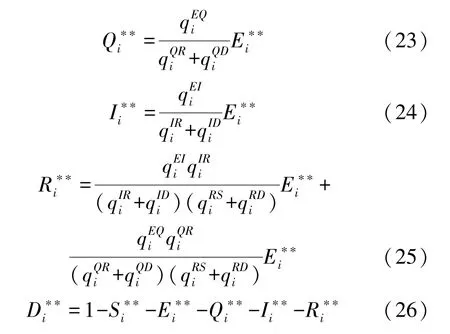
式中:

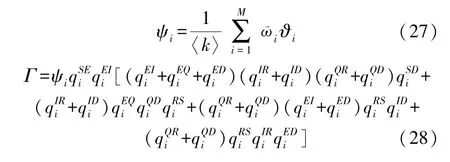
證畢。

定理1 得到的穩定點O*和O**含義不同。 其中，穩定點O*稱為無病穩定點，即I*=0，表示整個HWSNs 達到穩定點O*后被惡意程序成功攻擊感染的HSN 已不存在，也就是說，HWSNs 惡意程序最終將消亡。 穩定點O**稱為有病穩定點，即I**＞0，表示整個HWSNs 達到穩定點O**后被惡意程序成功攻擊感染的HSN 將大量存在，也就是說，惡意程序在整個HWSNs 中將處于傳染狀態。 因此，實際的HWSNs應用場景中，系統管理員應該采取相應的防御措施使得HWSNs 惡意程序傳播模型SEQIRD 趨向于無病穩定點O*，從而抑制HWSNs 惡意程序的傳播。

3 惡意程序傳播模型SEQIRD 的基本再生數

通過探尋HWSNs 惡意程序傳播模型SEQIRD的基本再生數，能以此判斷被惡意程序成功攻擊并感染的HSN 能夠感染其他與其直接通訊的節點的平均個數。 若基本再生數的值小于1，則表明一個被惡意程序成功攻擊并感染的HSN 能感染與其直接通訊的易感節點的個數少于1 個，這將使整個HWSNs 趨向于無病穩定點O*；若基本再生數的值大于1，則表明一個被惡意程序成功攻擊并感染的HSN 能感染與其直接通訊的易感節點個數大于1，這將使整個HWSNs 趨向于有病穩定點O**。 所以，計算得到模型SEQIRD 的基本再生數就能確定HWSNs 趨向于無病穩定點O*的條件，從而為系統管理員防御HWSNs 惡意程序傳播指明方向。

本文基本再生數的計算采用下一代矩陣法。 記ζ為HWSNs 惡意程序傳播模型SEQIRD 的基本再生數，則ζ=ρ(FV-1)，其中，ρ(·)代表矩陣的譜半徑，F代表當前HWSNs 在無病穩定點O*處狀態I的新增HSN 動態變化率矩陣，V代表HWSNs 在無病穩定點O*處狀態任意的兩個HSN 之間的動態轉換率矩陣，V-1代表矩陣V的逆矩陣。 通過這種方法計算惡意程序傳播閾值需要用到狀態E和狀態I，為了清楚地描述F、V的計算過程，引入臨時變量A、B、a11、a21、b11、b21。 令:

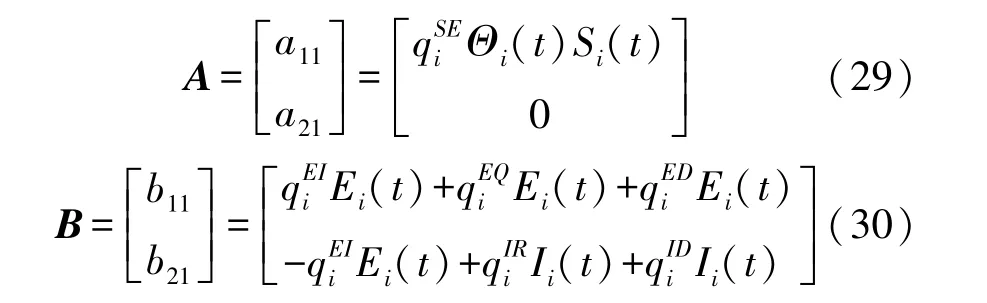
由式(29)可以得到新增HSN 動態變化率矩陣F為:

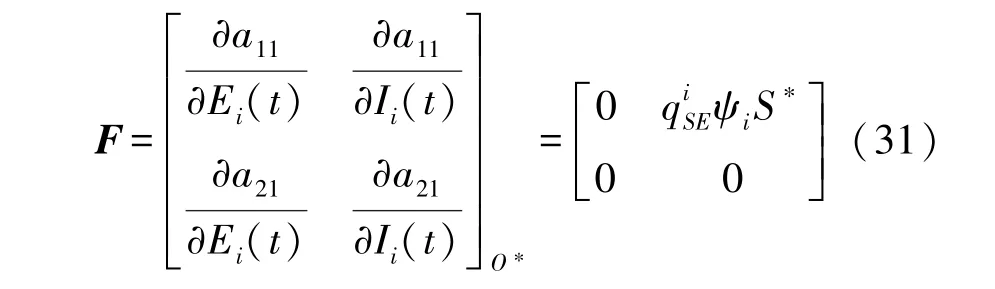
由式(30)可以得到動態轉換率矩陣V為:

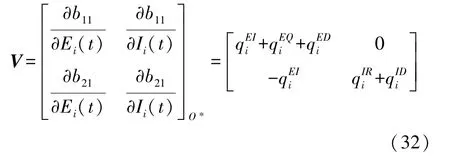
因此，可以得到HWSNs 惡意程序傳播模型SEQIRD的基本再生數ζ為:

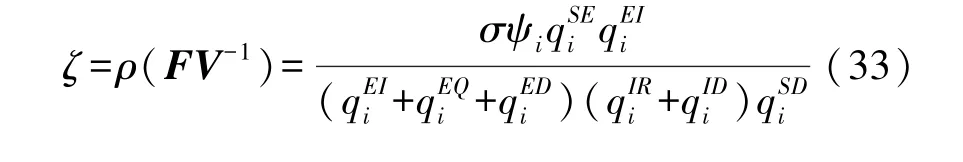
4 惡意程序傳播模型SEQIRD 的穩定性分析

對于HWSNs 惡意程序傳播模型SEQIRD 的穩定點O*和O**，只有系統管理員采取安全防御措施使模型SEQIRD 趨向于無病穩定點O*，才能有效控制HWSNs 惡意程序的傳播。 所以，本文僅研究無病穩定點O*的穩定性。

定理2當ζ＜1 時，HWSNs 惡意程序傳播模型SEQIRD 的無病穩定點O*局部漸進穩定；而當ζ＞1時，無病穩定點O*不穩定。

證明HWSNs 惡意程序傳播模型SEQIRD 的雅克比矩陣J為:

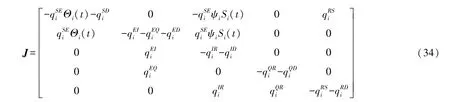
進一步，得到在無病穩定點O*的雅克比矩陣J(O*)為:

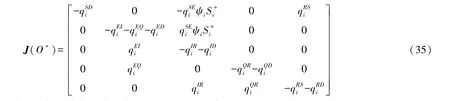
記λ代表特征值，E代表單位矩陣，則J(O*)對應雅克比行列式的三個特征值為:

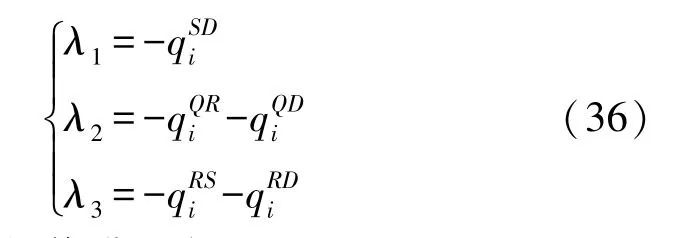
另外兩個特征值滿足方程:

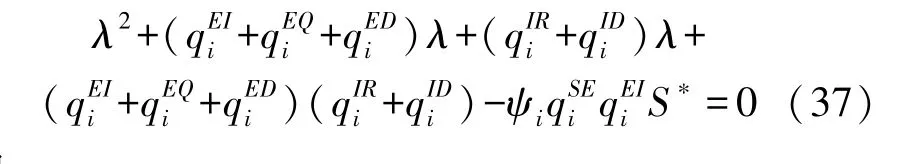
式中:

記

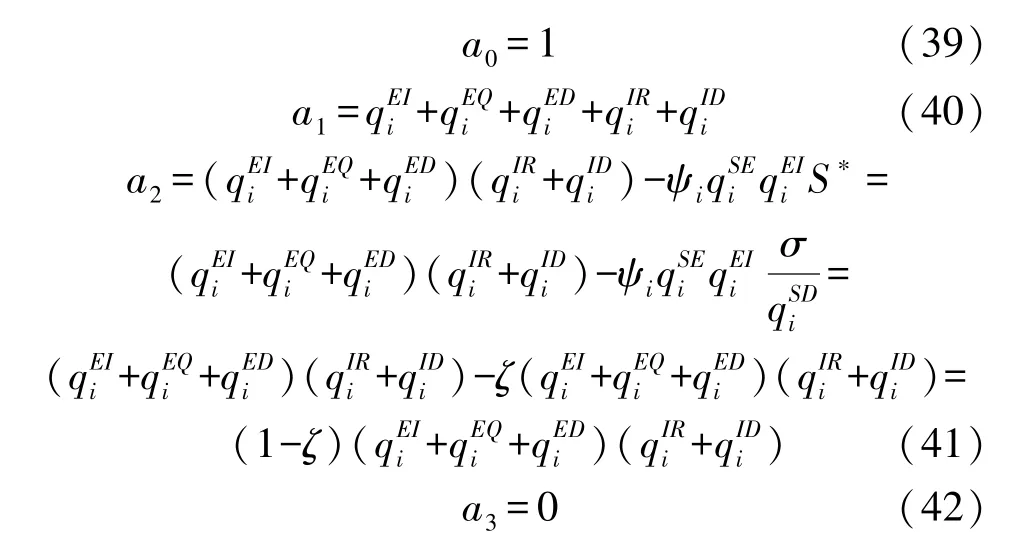
根據Routh-Hurwitz 判據[18]可知，

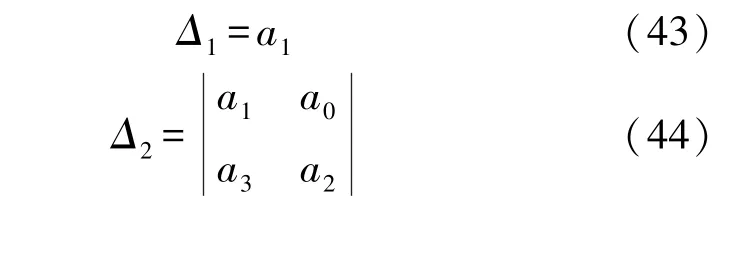
當Δ1和Δ2均大于0，即當a1＞0，a1a2-a0a3＞0時，方程對應的矩陣存在負實部特征值。 顯然，當ζ＜1時，滿足a1＞0，a1a2-a0a3=a1a2＞0，由Lyapunov穩定性定理可得，HWSNs 惡意程序傳播模型SEQIRD 的無病穩定點O*是局部漸進穩定的；而當ζ＞1 時，a1＞0，a1a2-a0a3=a1a2＜0，方程對應矩陣的特征值沒有負實部，所以，HWSNs 惡意程序傳播模型SEQIRD 的無病穩定點O*是不穩定的。 證畢。

定理2 結論揭示當ζ＜1 的時候，處于狀態S、E、Q、I、R、D且度為i的HSN 所占比例Si(t)、Ei(t)、Qi(t)、Ii(t)、Ri(t)、Di(t)最終分別趨向于、0、0、0、0、。 即當條件ζ＜1 滿足時，不管HWSNs 中已經被惡意程序成功攻擊并感染的HSN 的初始比例如何，只要系統管理員能夠保持目前的安全防御措施，HWSNs 惡意程序最終能被徹底清除，這對HWSNs 安全防御具有現實指導意義。

5 仿真及分析

通過仿真軟件MATLAB，驗證HWSNs 惡意程序傳播模型SEQIRD 無病穩定點O*的穩定性，以及關鍵轉換概率和對HWSNs 惡意程序傳播的影響。 具體仿真時，先將模型SEQIRD 變換成離散形式，即:

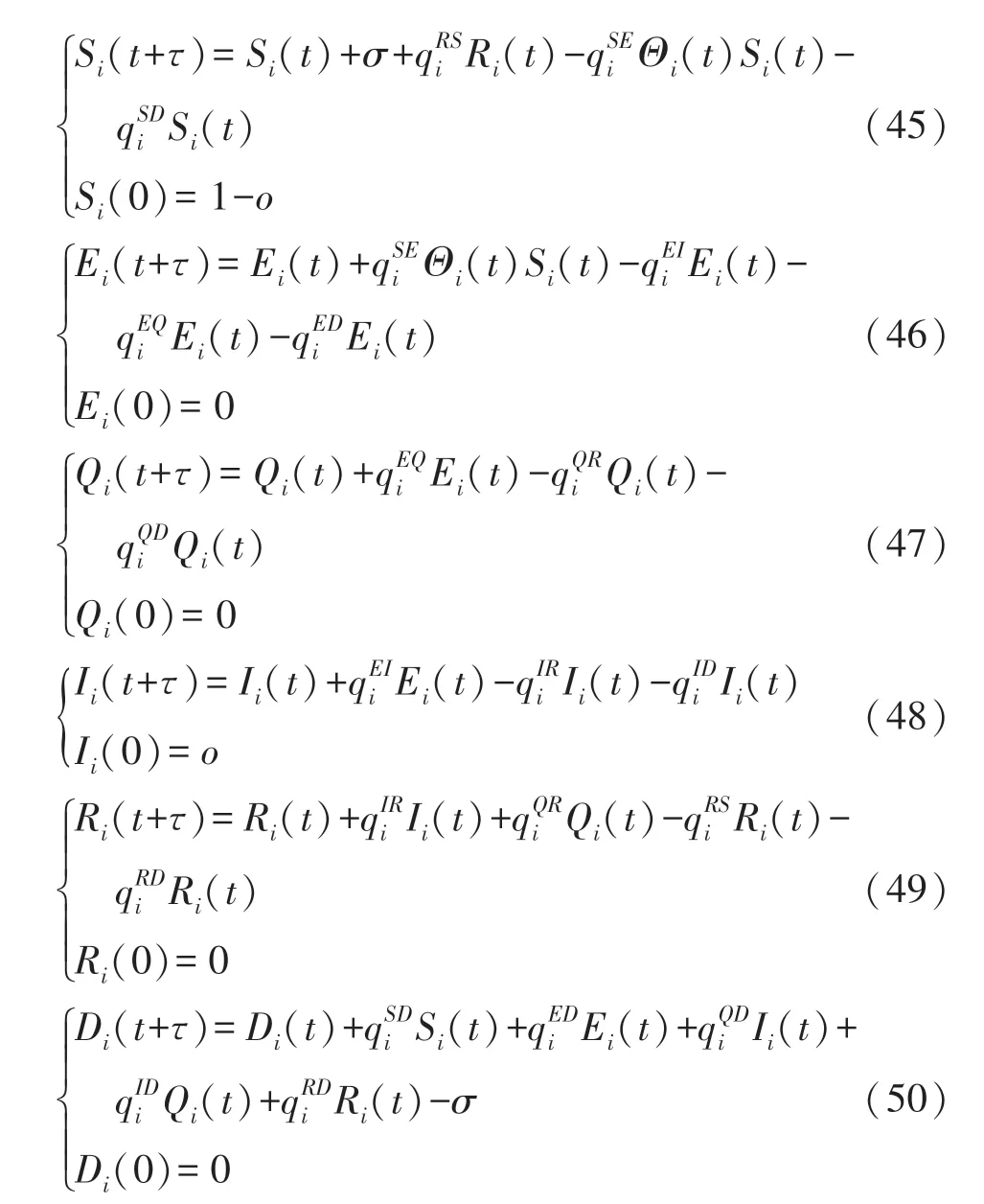
式中:τ代表離散的時間間隔。 這樣，通過使用Runge-Kutta 方法即可求解離散形式的SEQIRD 模型。 具體的仿真算法如算法1 所示。

算法1 驗證HWSNs 惡意程序傳播模型SEQIRD 的算法

仿真實驗中設置參數如下:M= 1000，表示HWSNs 中包含1000 個HSN；τ=1 h，表示離散的時間間隔是1 h。 一個HSN 的最小度為2，最大度為20，并且〈k〉=4，即HSN 的平均度為4。 一個HSN 被惡意程序成功攻擊并感染使狀態從S狀態轉換為E狀態的轉換率設置為βi，其中，β=0.01。 被惡意程序成功攻擊并感染的一個HSN，處于易感狀態的概率?i設置為ξiγ/(1＋μiγ)，其中，ξ=5，γ=0.5，μ=1。 根據HWSNs 的特性，其他參數分別設置為σ=0.01，=0.015。

5.1 驗證無病穩定點的穩定性

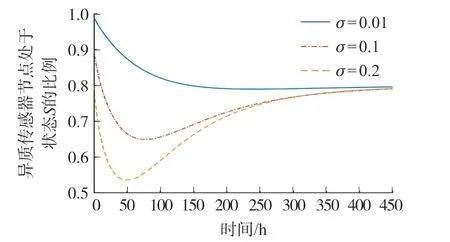
圖2 處于狀態S 的HSN 比例變化趨勢

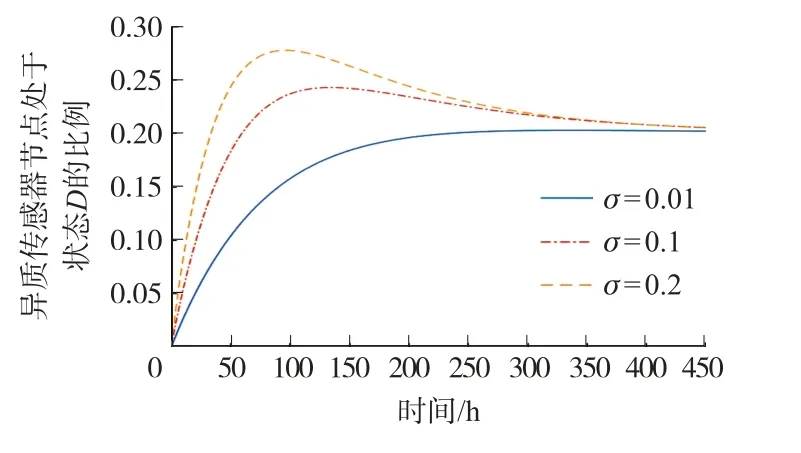
圖7 處于狀態D 的HSN 比例變化趨勢

在圖2 中，處于狀態S且度為i的HSN 比例Si(t)在不同的o取值下呈現不同的變化趨勢。 當o為1%的時候，Si(t)緩慢減少至約80%后，趨于穩定；當o為10%的時候，Si(t)緩慢減少至最低值約65%后，再緩慢上升最后穩定于約80%；當o為20%的時候，Si(t)緩慢減少至最低值約54%后，再緩慢上升最后穩定于約80%。 也就是說，最終Si(t)趨向于無病穩定點中的值0.8。

在圖3～圖6 中，處于狀態E、Q、I、R的HSN 比例Ei(t)、Qi(t)、Ii(t)、Ri(t)的變化趨勢在不同的o取值下保持一致。 由圖3 可以看出，Ei(t)逐步上升分別達到最高值約0.8%、6%和9.6%后，再緩慢下降最后趨向于0，這和無病穩定點中的值保持一致。 由圖4 可以看出，Qi(t)逐步上升分別達到最高值約0.3%、2.1%和3.1%后，再緩慢下降最后趨向于0，這和無病穩定點中的值保持一致。由圖5 可以看出，Ii(t)呈現下降趨勢最后趨向于0，這和無病穩定點中的值保持一致。 由圖6 可以看出，Ri(t)逐步上升分別達到最高值約1%、6%和9.3%后，再緩慢下降最后趨向于0，這和無病穩定點中的值保持一致。

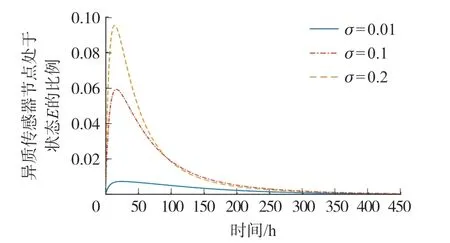
圖3 處于狀態E 的HSN 比例變化趨勢

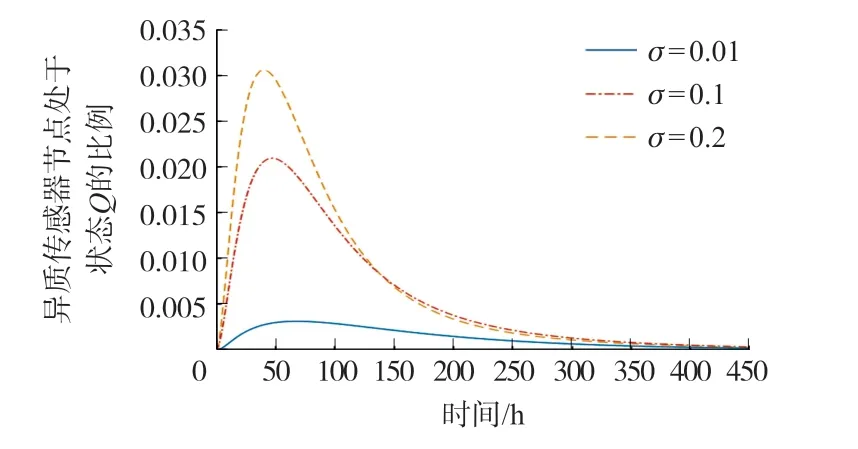
圖4 處于狀態Q 的HSN 比例變化趨勢

圖5 處于狀態I 的HSN 比例變化趨勢

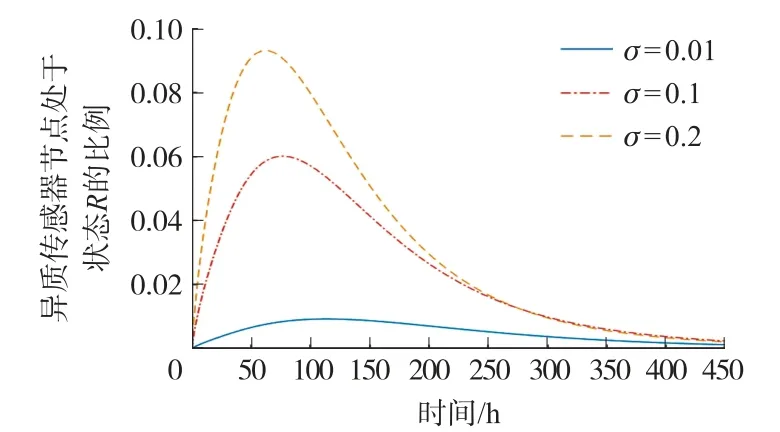
圖6 處于狀態R 的HSN 比例變化趨勢

在圖7 中，處于狀態D且度為i的HSN 比例Di(t)在不同的o取值下呈現不同的變化趨勢。 當o為1%的時候，Di(t)緩慢上升至約20%后趨于穩定；當o為10%的時候，Di(t)緩慢上升至最高值約24%后，再緩慢減小比例最后穩定于約20%；當o為20%的時候，Di(t)逐漸增大至最高值約27%后，比例再逐漸減小，最后穩定于約20%。 也就是說，最終Di(t)趨向于無病穩定點中的值0.2。

從而驗證了不管處于狀態I的HSN 初始比例設置值如何，只要滿足基本再生數ζ值小于1 的條件，經過惡意HSN 的反復攻擊感染和反復傳播，以及系統管理員采取相應的防御措施，對惡意HSN 的反復攻擊感染和反復傳播進行抑制，處于狀態S、E、Q、I、R、D且度為i的HSN 比例最終將分別趨向于無病穩定點。 實驗結果反映出在現實的HWSNs 管理過程中，系統管理員采取的安全防御措施要能影響并控制HWSNs 中的參數，達到定理2 中基本再生數值小于1 的條件，使得HWSNs 即使存在大量初期被惡意程序成功攻擊并感染的HSN，其中的惡意節點都將被治愈，從而有效控制HWSNs 惡意程序的傳播。

5.2 狀態轉移概率和對HWSNs 惡意程序傳播的影響

由式可知，一旦HWSNs 拓撲結構固定下來后，狀態轉移概率等參數值也相對固定，而狀態轉移概率和兩個參數變化較大，因此，本節通過仿真分析和對HWSNs 惡意程序傳播的影響，為系統管理員控制HWSNs 惡意程序傳播提供實驗依據。 實驗采用變量控制的思想，即將處于狀態I且度為i的HSN 初始比例設置為10%，其他狀態轉移概率參數的值保持不變，分別調整狀態轉移概率和參數值得到不同的仿真結果，再進行分析。

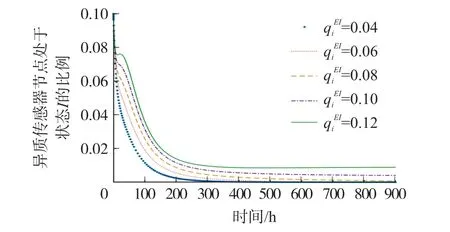
圖8 處于感染狀態I 且度為i 的HSN 比例在不同參數值下的變化曲線

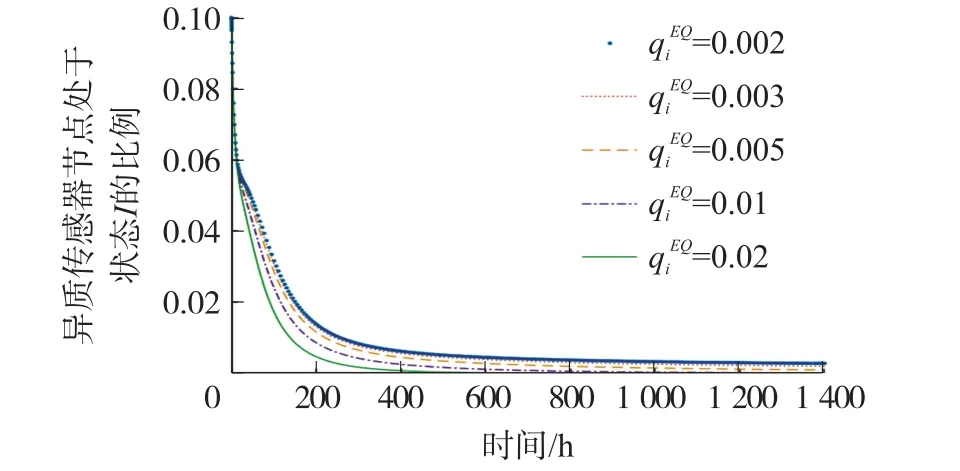
圖9 處于感染狀態I 且度為i 的HSN 比例在不同參數值下的變化曲線

6 結論

在擴展傳統傳染病模型SIR 基礎上，構建了基于潛伏和隔離機制的HWSNs 惡意程序傳播模型SEQIRD，分析了HWSNs 惡意程序的傳播特性。 通過引入單個HSN 的度來反映該節點異質的通信能力特性，解決了未體現HSN 異質特性的現有傳染病模型不能用于HWSNs 惡意程序傳播建模的問題。得到的HSN 狀態動態變化方程解決了現有模型沒有充分考慮HWSNs 惡意程序傳播具有隱蔽性、惡意HSN 被成功檢測而被隔離、HSN 因被惡意程序感染導致惡意破壞或自然損壞等情形的問題。 通過計算得到的模型SEQIRD 的穩定點以及基本再生數，明確了HWSNs 惡意程序消亡或傳播的閾值，進一步得到的HSN 易感狀態到潛伏狀態和隔離狀態的轉換概率閾值，為系統管理員制定一系列安全防御策略，從而遏制HWSNs 惡意程序傳播，并保證HWSNs 穩定、健康運行奠定理論基礎。

需要說明的是，本文考慮的HWSNs 惡意程序屬于同一種類型，而通常HWSNs 存在不同的惡意程序，因此，如何揭示HWSNs 中不同惡意程序的傳播機制是研究者值得進一步研究的實際問題。 另外，本文在借鑒經典傳染病模型思想時，考慮新加入的是易感節點，但如果加入的是打了安全補丁的節點，那么將得到用于描述狀態比例變化的不同的微分方程、不同的模型穩定點、不同的基本再生數，這樣得到的新模型是否還能保證穩定? 該問題符合實際的HWSNs，也是值得進一步研究的問題。