基于元共祖的基因組聯合育種模擬研究

龐志旭，張洪志，喬利英，王萬年，潘洋洋，劉文忠

(山西農業大學動物科學學院，太谷 030801)

基因組選擇(genomic selection, GS)目前已廣泛應用于畜禽遺傳評估。相對于基于系譜的最佳線性無偏預測(best linear unbiased prediction, BLUP)，基因組選擇能有效提高基于表型的預測準確性、縮短世代間隔和加快遺傳進展。然而，由于基因分型成本較高，通常只測定育種群中關鍵個體的基因型，因此，經典基因組預測方法只能利用部分個體的基因型和表型信息。為解決這一問題，Legarra等及Christensen和Lund提出了基因組選擇一步法(single-step genomic BLUP, SSGBLUP)。一步法通過有效整合群體所有個體(包括有基因型和沒有基因型信息個體)的系譜、表型和基因型信息，提高了基因組估計育種值(genomic estimated breeding value, GEBV)的準確性。

基因組選擇的準確性與參考群的大小密切相關，參考群規模越大，基因組選擇效果越好。而我國由于很多核心育種場規模較小，基因組選擇的效果不理想，對此我國制定了基因組聯合育種方案。使用SSGBLUP法進行基因組聯合育種，由于多個群體之間的基因型頻率不同，群體間沒有系譜上的關聯，不同群體個體間親緣關系為0，群體間不能進行有效的關聯，基因組關系矩陣與系譜親緣關系矩陣難以兼容，造成基因組聯合育種效果不理想。

為解決矩陣與矩陣不兼容的問題，Legarra等和Christensen提出了元共祖(metafounder)的概念。元共祖是用來描述基礎群內部關系的偽個體，可以理解為一個無限大小的配子池。基礎群的個體就是由配子池隨機抽取配對形成，各配子之間的共親關系(coancestry relationship)為2。多個元共祖之間的親緣關系為祖先關系矩陣(ancestral relationships)，基于矩陣與矩陣構建()矩陣。含元共祖的一步法(single-step method with metafounders, MF-SSGBLUP)使用0.5為等位基因頻率構建矩陣并與()矩陣聯合構建()矩陣，可以自動兼容矩陣與矩陣。

將MF-SSGBLUP應用于基因組聯合育種不僅可以解決矩陣和矩陣的兼容性問題，也解決了多個群體基因型頻率不同的問題，并且在()矩陣構建過程中加入了祖先關系矩陣，可以在不同群體個體間建立親緣關系，將多個群體產生關聯。

為了研究MF-SSGBLUP在基因組聯合育種中的有效性，本研究基于多個模擬群體進行以下研究：1)比較MF-SSGBLUP法和SSGBLUP法構建的矩陣與矩陣的兼容性；2)比較MF-SSGBLUP、SSGBLUP和BLUP的遺傳參數估計結果；3)對MF-SSGBLUP在基因組聯合育種中的使用效果進行評估。

1 材料與方法

1.1 數據模擬

本研究使用QMSim模擬2個具有不同遺傳力(0.1和0.3)的限性性狀，表型方差設置為1，每個性狀進行10次重復。歷史群體起始規模為5 000頭，經過1 000個世代，群體衰減為250頭，再經過100個世代，群體擴增為1 000頭，通過群體規模的波動達到與真實群體相似的連鎖不平衡(linkage disequilibrium，LD)程度，并且建立了突變漂變平衡。整個歷史群體公、母比例保持1∶1，個體間采取隨機交配。模擬3個擴增群體(Line1、Line2、Cross)，世代數為10，每個世代增長率為60%，個體間采取隨機交配。擴增群體模擬策略為：1)在歷史群體的最后一個世代中抽取真實育種值較高的10頭公畜和100頭母畜構成Line1的初始群體，抽取真實育種值較低的10頭公畜與100頭母畜構成Line2；2)從Line1的第10世代中抽取100頭公畜，從Line2的第10世代中抽取100頭母畜，構成Cross1的初始群體(圖1)。

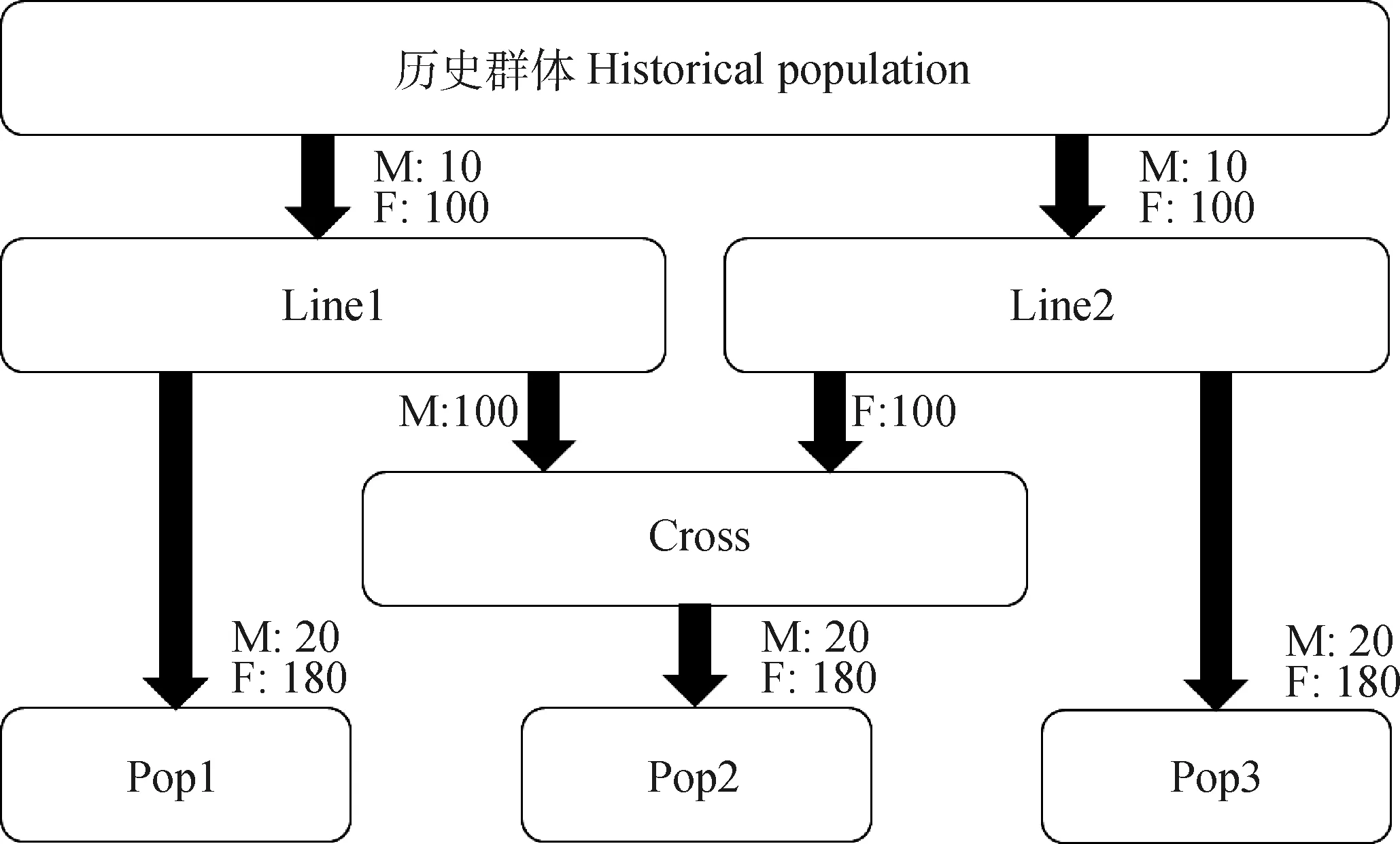
Line1、Line2和Cross代表不同的擴繁群體，Pop1、Pop2和Pop3代表不同的當代群體Line1, Line2 and Cross correspond to different expansion populations, while Pop1, Pop2 and Pop3 correspond to different current populations圖1 群體結構模擬策略Fig.1 Simulation strategy for population structures

分別從3個擴增群體的第10世代中抽取EBV高的20頭公畜和180頭母畜構成3個當代群體Pop1、Pop2和Pop3(圖1)，世代數均設為10代，設置3個元共祖對應3個群體。模擬中，每代公畜淘汰率為30%，增長率為10%；母畜淘汰率為20%，增長率為10%。每代公、母畜間隨機交配。假定所研究畜種為單胎，每頭母畜后裔數為1，后裔公、母各半，選擇EBV高的個體留種。保留當代群體第1～9 世代所有母畜的表型信息，將第1～9世代作為參考群，將第10個世代作為候選群。

本試驗模擬奶牛的基因組，共設置29對染色體，全長為2 333 cM，性狀受到1 000個隨機分布在全基因組中的數量性狀基因座(quantitative trait loci, QTL)影響。QTL效應值服從形狀參數為0.4的伽馬分布。模擬50 000個均勻分布于全基因組上的SNP標記。設置起始歷史群體SNP和QTL等位基因頻率均為0.5，每個位點突變率為10，標記位點的錯誤率為0.5%。選取群體后5代有后裔的公畜和最后2個世代的所有個體都進行基因分型。對模擬產生的基因型數據進行質量控制，刪除次要等位基因頻率低于5%的基因型。經過質量控制，對于為0.3的模擬數據，保留的SNP標記數為47 313，10次重復的方差為173.5；對于為0.1的模擬數據，保留的SNP標記數為47 289，10次重復的方差為168.7。

1.2 基因組預測模型

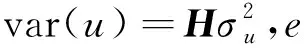
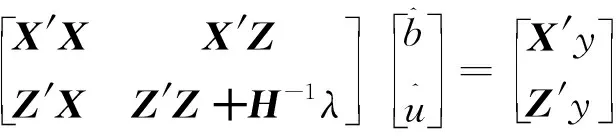
(1)

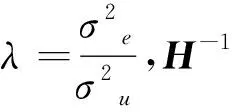
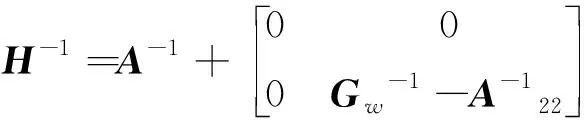
(2)

其中，=(1-)+w，為加權因子(設為常數0.05)，矩陣能避免矩陣無法求逆的問題，且通過混合矩陣解釋了一些基因型標記未能解釋的效應。考慮到矩陣與矩陣兼容性的問題，使用矯正后的矩陣：=β+，其中，和通過以下方程組求解得出：

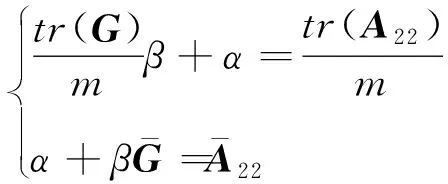
(3)

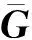
1.2.2 MF-SSGBLUP MF-SSGBLUP法的MME為：

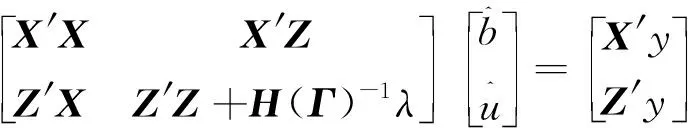
(4)

其中，()為：

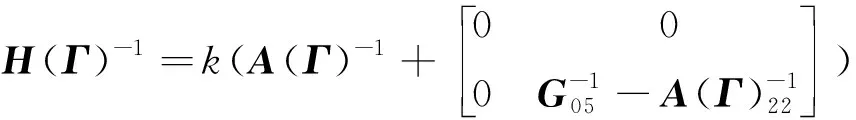
(5)

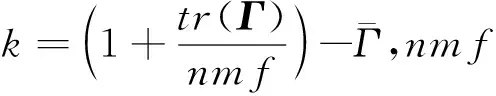
祖先關系矩陣構建方法為：=8=8()，其中是一個矩陣，行數為總標記數，列數為群體數，的元素代表第個標記在第個群體中的頻率；是維度等于群體數的一個方陣，其中對角線元素為該群體基因型頻率的方差，非對角線元素為兩個群體間基因型頻率的協方差。本研究使用兩種方法計算矩陣，以對兩種方法的性能做比較。一種方法是只使用基因型數據來估計的原始方法(na?ve，NAI)：

=μ+

(6)

(7)

其中，為基因分型個體第個位點的基因型，由{0,1,2}組成；是一個將元共祖與后代個體聯系起來的矩陣，每行元素之和為1；為各群體在第個位點的基因型均值向量；為誤差向量。所有位點的基因型均值為=[…]。由于，=2，所以，=2()。

第二種是同時利用基因型與系譜信息計算矩陣的廣義最小二乘法(generalized least squares，GLS)：

=μ+u+

(8)

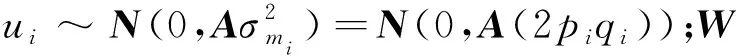
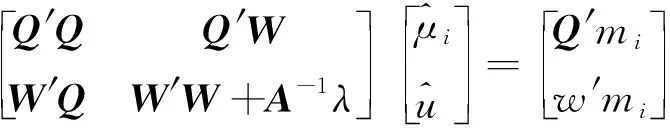
(9)

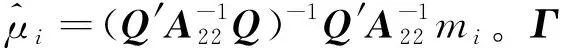
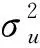
1.3 數據分析

1.3.1 基因組關系矩陣與系譜親緣關系矩陣的兼容性 用對角線元素與非對角線元素之間的相關系數()、回歸系數()和回歸截距()3個指標來評價矩陣與矩陣之間的兼容性。相關系數是矩陣與矩陣對角線元素之間和非對角元素之間的皮爾森相關系數：

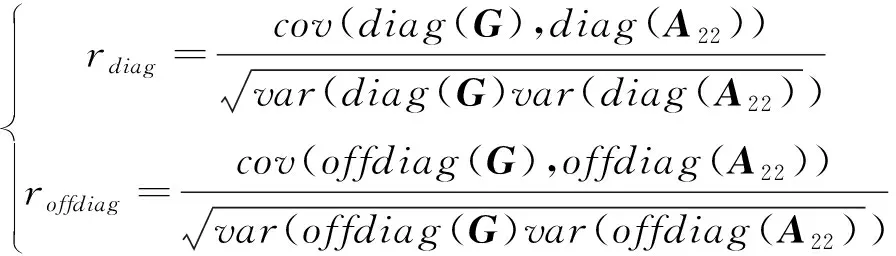
(10)

其中，和分別對應對角線元素與非對角線元素，為協方差，為方差，相關系數越高表示相關性越好。

回歸系數與回歸截距是通過構建矩陣對角線元素(非對角線元素)對矩陣對角線元素(非對角線元素)的回歸方程：

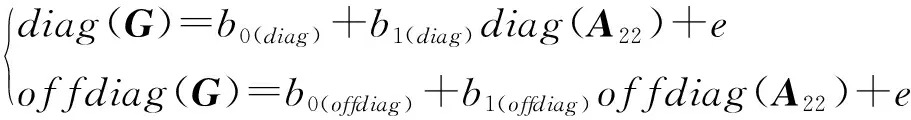
(11)

回歸系數越接近于1，回歸截距越接近于0，表示無偏性越好。

1.3.2 模型評價 用準確性(accuracy)和無偏性(bias)來比較不同模型的性能。準確性通過EBV與TBV之間的相關系數衡量：

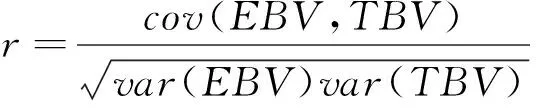
無偏性用GEBV對TBV的回歸系數來衡量：

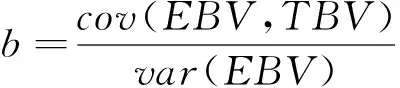
回歸系數越接近于1越好，用=|1-|衡量無偏性。

2 結 果

2.1 群體模擬結果

模擬的3個當代群體(Pop1、Pop2和Pop3)，個體總數為8 430。其中，參考群和候選群個體分別為7 404和1 026個，基因分型個體為2 103個，具有表型的個體約為3 702個。

為了評估模擬產生的群體遺傳結構，利用3個群體的基因組標記信息進行主成分分析(principal component analysis, PCA)。由于10次模擬的群體遺傳結構相似，僅展示第1次模擬結果(圖2)。為0.1時，群體前兩個主成分所解釋的方差占總方差的百分比分別為9.906%和6.081%；為0.3時，分別為9.049%和7.479%。表明模擬的3個群體具有明顯的遺傳差異。

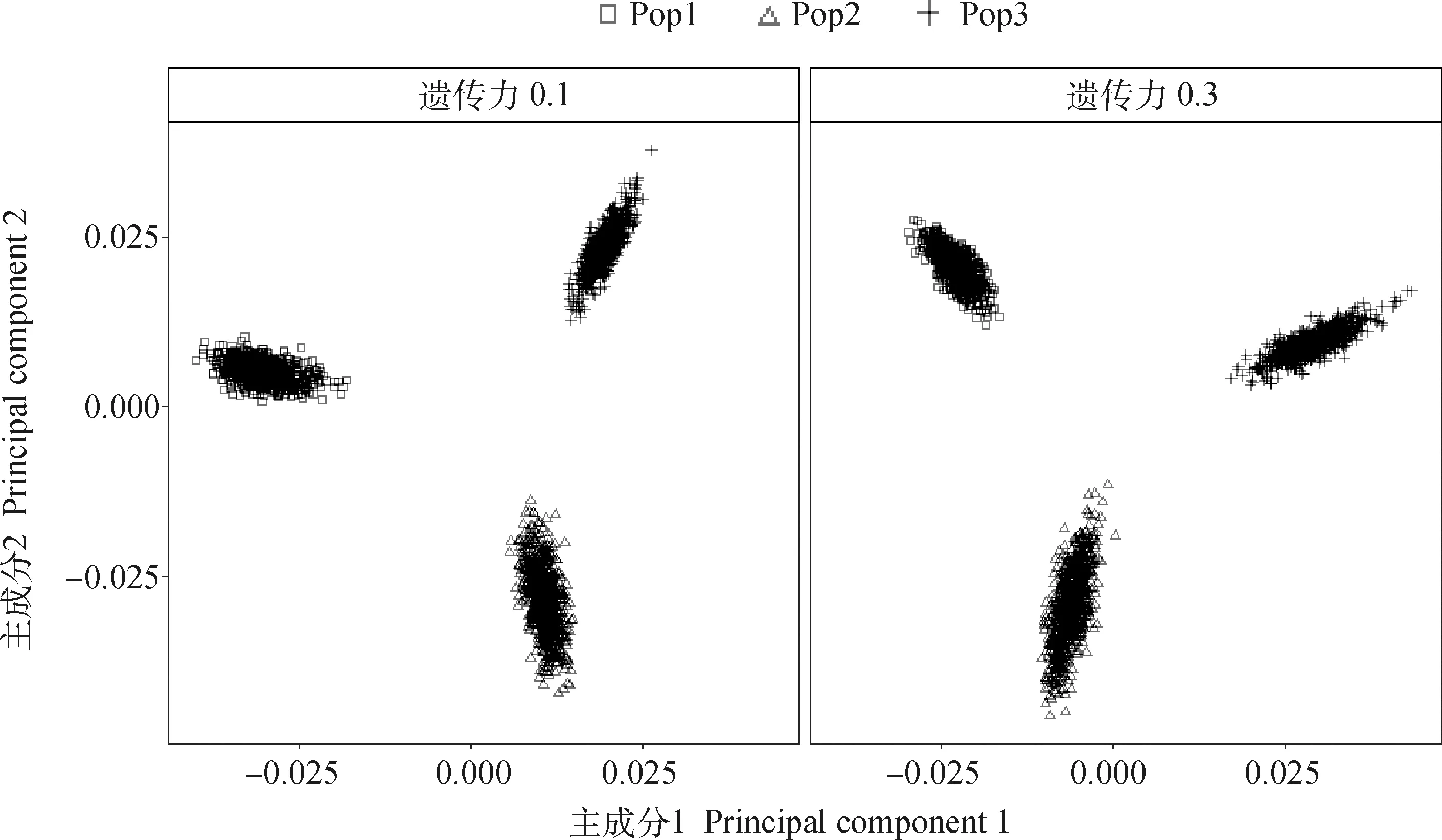
圖2 模擬的3個群體間的遺傳差異Fig.2 The genetic differences among 3 simulated populations

2.2 Γ矩陣的估計

使用GLS和NAI法對矩陣進行估計。為0.1時，10次重復的均值為：

為0.3時，10次重復的均值為：

矩陣為元共祖之間的關系矩陣，元素的值反映了元共祖之間的親緣關系。在不同下，矩陣差異不大，說明不同下基礎群個體間親緣關系相似。矩陣對角線元素的值普遍大于非對角線元素，表明在同一個基礎群體內的個體親緣關系高于不同基礎群體個體間的親緣關系。對角線元素略小于的對角線元素，非對角元素之間沒有差異。

2.3 不同方法兼容性的比較

兼容性通過親緣關系矩陣與基因組關系矩陣的對角線(非對角線)元素的相關系數、回歸系數和回歸截距來說明，其中相關系數與回歸系數越接近于1，回歸截距越接近于0兼容性越好。通過矩陣和矩陣分別構建()和()矩陣，并計算與矩陣的兼容性，用常規SSGBLUP法構建的矩陣與進行對照，結果見表1。在不同下，()～和()～對角線(非對角線)元素相關系數0.750～0.775(0.954～0.964)、回歸系數0.859～0.992(0.639～0.812)和回歸截距-0.013～0.135(0.071～0.098)均顯著(<0.05)優于～相關系數0.508～0.572(0.723～0.738)、回歸系數0.543～0.652(0.683～0.745)和回歸截距0.374～0.493(0.134～0.139)，表明元共祖法構建的矩陣與矩陣間兼容性更好(表1)。

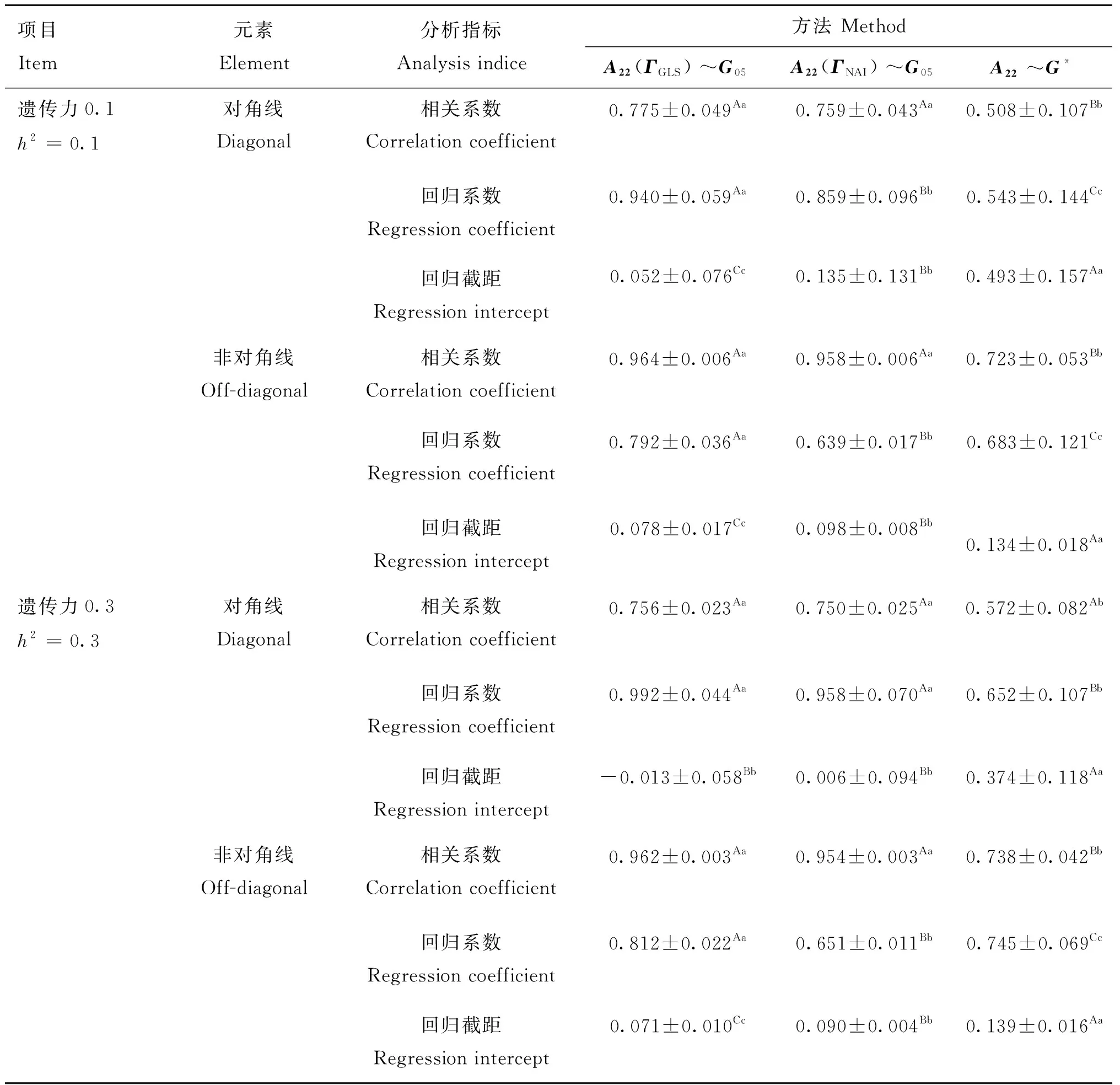
表1 3種方法構建的G和 A22矩陣的兼容性比較Table 1 Comparison of compatibility between G and A22 matrices constructed by 3 methods

2.4 方差組分的估計

表2為10次重復下MF-SSGBLUP(GLS)、MF-SSGBLUP(NAI)、SSGBLUP和傳統BLUP對方差組分和估值的均值和方差與當代群體遺傳參數的對比。在初值為0.1和0.3的群體中，4種方法對的估計值介于0.138～0.173和0.273～0.340，與當代群體遺傳力0.107和0.296相符。此外，兩種MF-SSGBLUP在不同下對方差組分的估值比SSGBLUP和BLUP法更接近于真值，表明MF-SSGBLUP法在遺傳參數的估計上要優于SSGBLUP和傳統BLUP法。

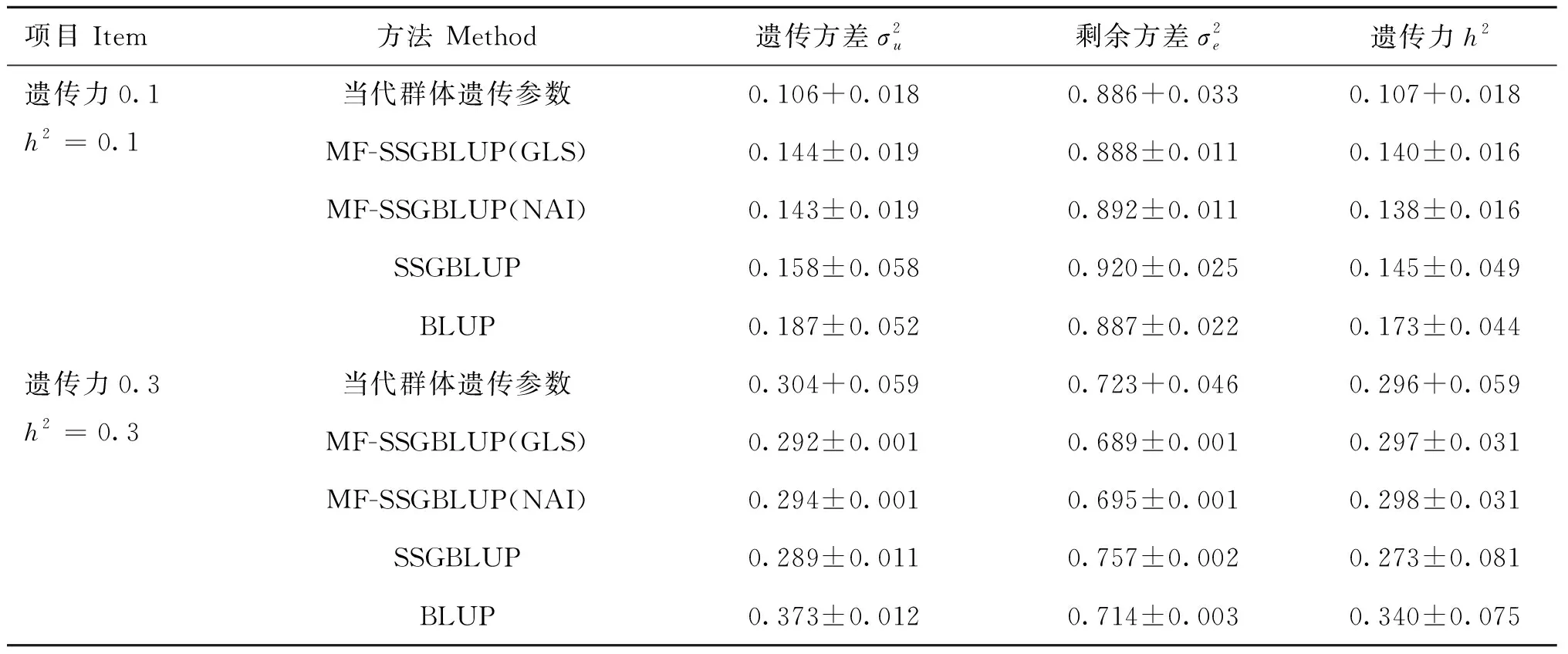
表2 4種方法估計的方差組分和遺傳力Table 2 Estimated variance components and heritabilities by 4 methods

2.5 不同模型預測效果

圖3為4種方法估計育種值的準確性和無偏性。在為0.1情況下，兩種MF-SSGBLUP 的準確性均為0.888，MF-SSGBLUP(GLS)的無偏性均值為0.030，MF-SSGBLUP(NAI)的無偏性均值為0.032，SSGBLUP為0.863和0.066，傳統BLUP為0.854和0.078；在為0.3情況下，兩種MF-SSGBLUP的準確性和無偏性均值均為0.908 和0.029，SSGBLUP為0.876和0.057，傳統BLUP為0.871和0.067。不同下，兩種MF-SSGBLUP的準確性與無偏性顯著優于SSGBLUP與BLUP法(<0.05)，而MF-SSGBLUP的兩種算法(GLSNAI)間則無顯著差異。以上結果表明，在基因組聯合育種中，MF-SSGBLUP法有一定優勢。

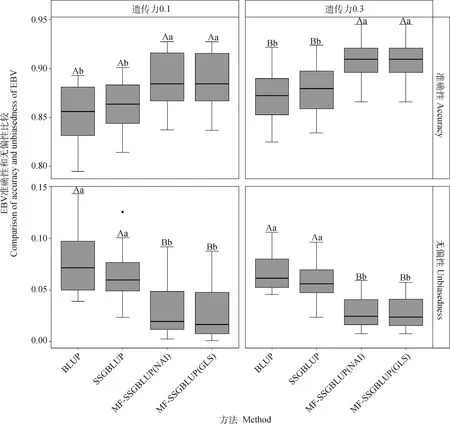
不同大寫字母表示差異極顯著(P<0.01)，不同小寫字母表示差異顯著(P<0.05)Different capital and lowercase letters mean significant differences at P<0.01 and P<0.05, respectively圖3 4種方法估計育種值的準確性與無偏性比較Fig.3 Comparison of accuracy and unbiasedness of estimating breeding values by 4 methods

3 討 論

用MF-SSGBLUP法進行遺傳評估已有報道，并且均表現出一定的優勢，但是在基因組聯合育種中還未應用。本研究模擬了不同(0.1和0.3)的性狀，使用傳統BLUP法、SSGBLUP法和MF-SSBLUP法進行遺傳評估。其中，用GLS和NAI兩種算法估計祖先關系矩陣。Bradford等指出，矩陣不依賴表型信息，只與基因型信息與系譜信息相關。本研究在不同下獲得的矩陣數值上差異不大，是因為不同下模擬的群體結構類似。不同情況下，GLS法和NAI法所得的矩陣非對角線元素間差異不大，而對角線元素則有明顯差異，即NAI法所得的元共祖近交系數高于GLS法。Garcia-Baccino等發現NAI法對矩陣中的元素估值偏高，GLS法能有效獲得矩陣的無偏估值，與本研究結果相符。本試驗中基因分型個體都是經過了多個世代的選擇，部分基因型頻率漂變到極端值， NAI法忽略了這一部分的影響，GLS法考慮了基因型在世代間的傳遞，將系譜信息納入模型之中，因而更為準確。

對比不同方法構建的矩陣與矩陣，發現()～和()～兼容性要優于～，這與Kudinov等在丹麥紅牛上的研究成果相似。Christensen指出基因分型個體與所有個體間育種值平均值的差異導致了矩陣與矩陣的不兼容。一些研究通過調整矩陣使其與矩陣相兼容，但是都沒有從本質上解決問題。元共祖法與之相反，通過調整矩陣，達到與基因型關系矩陣相兼容的目的。VanRaden指出，矩陣中的元素為親緣相關的期望值，然而在基因組聯合育種中由于多個群體在系譜上沒有關聯，不同群體個體間相關關系為0，這與基因組關系矩陣在不同群體個體間親緣相關大于0的情況相悖。基于元共祖構建的親緣關系矩陣，不同群體中個體間的相關關系通常不為0。()～在非對角線元素的回歸系數與回歸截距上要優于()～，這可能是因為GLS法獲得矩陣的估計值比NAI法無偏性更好。

在Garcia-Baccino等的研究中，傳統BLUP估計的更接近于真值。然而，本研究顯示，兩種算法下，MF-SSGBLUP法遺傳參數估值的無偏性較好，可能是由于3個模擬群體沒有系譜關聯導致了傳統BLUP對遺傳參數估計的準確性下降。

Garcia-Baccino等的研究指出，在基因組選擇中，MF-SSGBLUP比SSGBLUP法能獲得更高的準確性與更小的偏差。Bradford等設置了3個 不同的元共祖，對于為0.3和0.1的性狀，與SSGBLUP和BLUP相比，MF-SSGBLUP能獲得更高的準確性。而且，Bradford等在系譜缺失情況下，發現MF-SSGBLUP法所得結果的一致性最好，能有效減少由于系譜缺失造成的偏差。Xiang等和Van Grevenhof等分別在二元雜交系統與三元雜交系統中驗證了元共祖方法的優越性。本研究中，兩種算法的MF-SSGBLUP法的遺傳評估準確性均顯著高于SSGBLUP和BLUP法，且EBV的偏差更小，與前人研究結果相似。兩種MF-SSGBLUP算法的準確性與無偏性沒有明顯差異，說明GLS和NAI兩種算法估計的矩陣對EBV的準確性沒有較大影響。但是，GLS能獲得更加無偏的矩陣，且通過構建的矩陣與矩陣兼容性更好，所以，建議使用MF-SSGBLUP(GLS)進行基因組聯合育種。

4 結 論

用MF-SSGBLUP對多個模擬群體進行基因組聯合育種研究，發現MF-SSGBLUP通過估計多個系譜獨立群體的元共祖間親緣關系，優化多群體聯合育種的關系矩陣，可有效提高遺傳力和育種值的估計準確性和無偏性。因此，MF-SSGBLUP能有效解決多群體間系譜獨立和基因頻率差異的問題，在基因組聯合育種中具有良好應用潛力。