無限稀釋氯化氫水溶液中離子遷移數的測定

許新華，吳梅芬，王曉崗

同濟大學化學科學與工程學院，上海 200092

1 實驗原理和數據分析方法

1.1 電解質溶液濃度c → 0時遷移數與濃度的關系

根據Debye-Hückel-Onsager電導率方程[4]，對于1-1價型電解質(如HCl)，其離子摩爾電導率λ與溶液濃度c的關系可以表達為：

式中λ∞是濃度為零時的離子極限摩爾電導率。在25 °C水溶液中，若濃度c的單位是mol·L-1，摩爾電導率的單位是10-4S·m2·mol-1，則p= 30.1，q= 0.229[5]。據此，正離子的遷移數可以表達為：

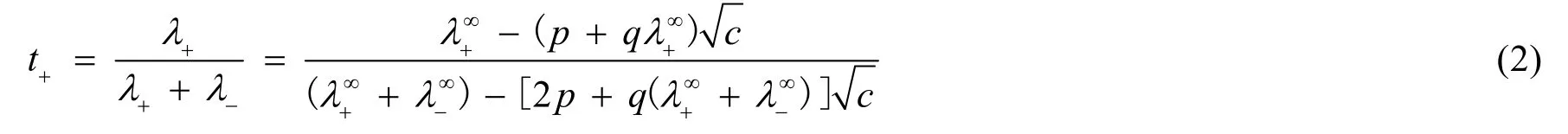
若令

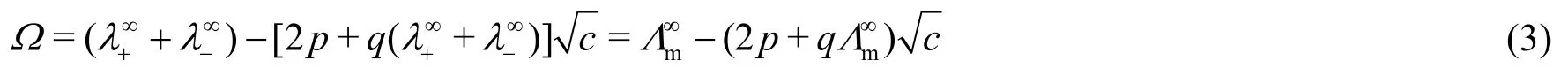
式中Λ∞m為無限稀釋條件下電解質溶液的極限摩爾電導率。正離子的極限遷移數與離子極限摩爾電導率的關系為：

結合方程(3)、(4)，將方程(2)分式分子中的參數q消去，則方程(2)可以重排為：

方程(5)即為在電解質濃度趨近于0時離子遷移數與濃度的關系式。由于參數?也是濃度c的函數，因此t+既不與c成線性關系，也不與c1/2成線性關系。

由方程(5)可以推出無限稀釋條件下，t+vs.c1/2曲線的斜率在c→ 0時應滿足：

移動機器人可以自行組織運行和自主規劃，其基礎在于定位精度和導航準確性。通過導航定位可獲得機器人所在的位置、方向，再分析實驗數據，建立運動模型，從而完成路徑的規劃和目標跟蹤。

可見，該極限斜率與t∞ +偏離0.5的差值成正比，與電解質極限摩爾電導率成反比。如果離子極限遷移數t∞ +＞ 0.5，則該極限斜率為正值，正離子遷移數隨溶液濃度增大而增大；反之亦然。

1.2 實驗測量數據外推離子極限遷移數的方法

方程(1)僅適用于電解質溶液濃度無限接近于零的極限濃度區[5]，如對于1-1價型電解質，c＜ 0.001 mol·L-1。界面移動法實驗中電解質溶液的濃度范圍一般為0.01-0.20 mol·L-1，因此上述方程對實驗數據的處理是無效的。如圖1所示，實驗數據的測量區域與理論方程的適用區域是分離的，在兩條紅色虛線之間的區域就是所謂的“數據鴻溝”。若采用數據擬合方法將實驗測量曲線(圖1中的黑實線)外推至縱坐標軸，由于該曲線為非線性曲線，可能產生多個滿足誤差要求的擬合結果，從而導致數據分析結果的不確定性，即落入所謂的“局域最小化”陷阱[6]。

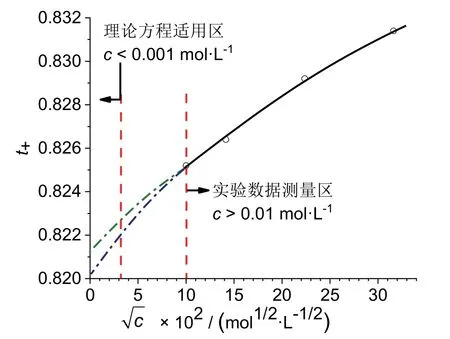
圖1 “實實鴻溝”和擬合不確定性

為得到離子遷移數t+與溶液濃度c之間的線性關系，Longsworth[7]借鑒了Shedlovsky處理電導率與溶液濃度關系的成功案例[8,9]。首先，對實驗測得的每一個濃度c對應的遷移數t+，都可以根據方程(5)計算出一個“表觀極限遷移數t∞ +”，記為t0，計算公式為：

注意式中的Ω也與濃度c有關。實實證明，表觀極限遷移實t0與c成線性關系，即：

將t0與c關系曲線做線性擬合，并外推到c= 0，所得截距即為正離子的極限遷移實t∞ +。

理理(8)得到的極限遷移實t∞ +是否符合1.1節中理理理理的要求呢？可以將理理(7)、(8)聯立求解，得到遷移實t+與溶液濃度c的關系為：

根實理理(9)，計算t+vs.c1/2的極限斜率為：

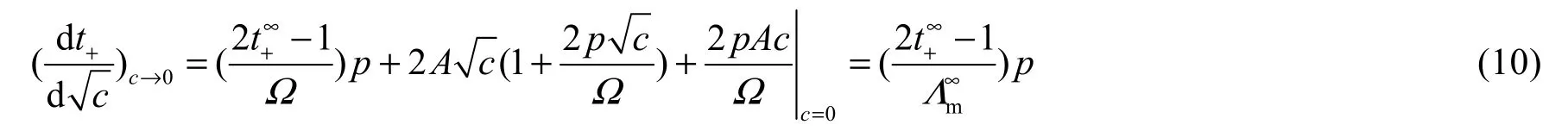
該極限斜率與理理(6)完全相同，說明理理(8)線性擬合外推得到的極限遷移實t∞ +代入理理(9)后，其在無限稀釋濃度附近理域內的變化趨勢是符合Debye-Hüchel-Onsager理理模型的。

由理理(8)外推得到極限遷移實t∞ +后，就可以通過理理(9)計算出高濃度條件下離子遷移實t+vs.c1/2的擬合曲線，并考查實實實實實實與理理計算結果之間的相符理度。

2 教學實實可行性實證

上述理法能否應理于本科教學實實，是一個尚有待檢實的問題。根實文獻實實[10]，在實實實實濃度范圍內，H+的遷移實變化范圍為0.82-0.83之間。采理常規實實教學手段獲得的實實實實是否能夠以滿意的精度符合理理(8)的線性關系，是檢實實實設計是否成功的關鍵。此外，最終外推得到的H+極限遷移實的值與文獻值之間的誤差大小，也是重要的考實因素。

在現有的物理化學實實教材中，界面移動法實定離子遷移實的實實原理和理法已有詳細描述，在此不再重復。經典實實采理金屬鎘(Cd)作為陽極，但是鎘及其電解產物鎘離子的毒性較大[11,12]，不理合一次實實中大實或多批次使理。吳舒婷等[13]提出可以理銅電極代替鎘電極，對0.1 mol·L-1鹽酸溶液中H+遷移實的實實表明，采理銅電極或鎘電極所得的結果一致，并與文獻值相符。本實實以銅電極為電解陽極，以鉑電極為電解陰極，用0.05%甲基紫溶液為指示劑，測定濃度為0.02-0.20 mol·L-1范圍內的一系列鹽酸溶液的遷移數，并外推至無限稀釋條件下的極限遷移數。

實驗采用恒電流法，電遷移管為內徑8 mm玻璃直管，總刻度容量2.0 mL，刻線分度0.1 mL，帶恒溫水夾套。陽極采用4 mm2銅導線，插入端剝出長度約5 mm的銅線，用細砂紙打磨去除氧化層后清洗干凈備用；陰極采用鉑絲電極。直流電源為LQY型直流恒流電源(南京桑力電子設備廠)，電流測量采用指針式精密直流電表(最小分度0.05 mA)。實驗中需根據不同鹽酸溶液的濃度調節電流大小，使得溶液界面掃過0.1 mL體積的時間不低于8 min。為保證界面清晰，指示劑的用量固定為每100 mL溶液中含指示劑5 mL。

圖2中給出了根據三組學生實驗測量結果計算得到的表觀極限遷移數t0vs.鹽酸溶液濃度c數據點及其對應的擬合直線。三組實驗數據采用同一系列濃度的鹽酸溶液，但是由不同學生實驗小組在不同儀器上完成。三個實驗獲得的t0vs.c擬合直線成果如下：

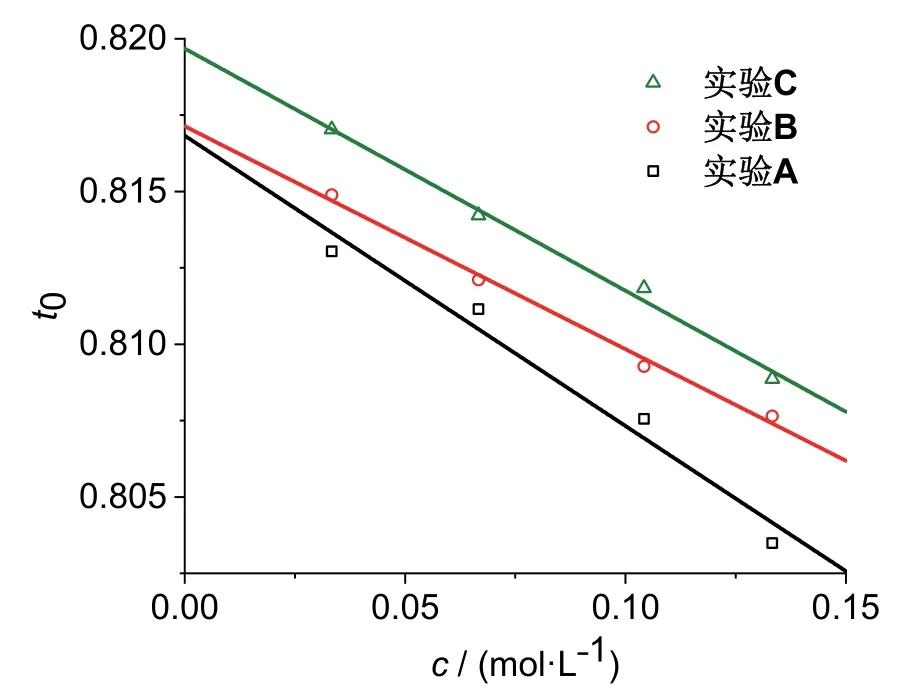
圖2 t0 vs. c實驗數據及其擬合直線

從實驗數據可以看出，雖然三組平行實驗數據不是完全一致，其中實驗A的擬合直線線性也不是非常理想，但是作為一個學生實驗而言，有以下幾個方面的可取之處：

(1) 三組平行實驗t0vs.c的擬合直線均表現出負斜率，即t0值隨溶液濃度c的下降而上升，這是符合文獻對鹽酸溶液的測量結果的[7,10]；

(2) 三組平行實驗獲得的擬合直線截距，即H+的極限遷移數t∞ +分別為0.8168、0.8171和0.8197，平均值為0.8179 ± 0.0013，平行實驗的數據重現性較好，標準偏差較小，相對偏差 ＜ 1.6‰。

根據文獻數據[7,10,14]，鹽酸溶液中H+的極限遷移數t∞ += 0.82085，我們實驗測量的結果均低于文獻值，相對誤差為3.6‰ (其中實驗A的相對誤差最大，為5.0‰)，略高于平行實驗數據間的相對偏差。由于平行實驗測量數據均偏向文獻值的低側，因此實驗值與文獻值間的誤差應歸屬于系統誤差，其產生的主要原因是實驗中使用銅電極代替傳統的鎘電極，而Cu2+不像Cd2+具有明顯的顏色，因此必須在鹽酸溶液中額外添加酸堿指示劑以形成清晰的界面，實驗中還發現，通電一段時間后陽極附近的溶液顏色逐漸變淺直至變為無色，說明添加的指示劑發生了電氧化脫色反應，這個現象也在相關文獻中被注意到[15]。脫色反應消耗了陽極氧化給出的一小部分電子，導致用于溶液中離子遷移的電量相應減小，使得實驗測得的離子遷移數相應降低。由此可見，采用“銅電極+酸堿指示劑”體系代替傳統的鎘電極，會引入一個實驗系統誤差，且該誤差略大于平行實驗間的相對誤差。甲基紫在本實驗條件下的電氧化脫色反應尚未見研究報道，粗略觀察發現，0.01 mol·L-1溶液的初始脫色液體體積增長量與界面移動體積之比約為1 : 6，估算消耗于電氧化脫色反應的電量約為總電量的1.5%；隨著電解進行，陽極附近溶液中的指示劑基本耗盡，遠端溶液中的指示劑需通過緩慢擴散才能到達陽極，脫色反應效應明顯減弱，實驗中觀察到電解實驗初始階段測得的遷移數明顯偏低，隨著電解的進行，當界面移動體積大于0.5 mL后，測得的遷移數基本趨于穩定；同時，當溶液濃度增大后，由于指示劑濃度始終不變，脫色反應消耗的電量比例相應降低，使得測量誤差也隨之降低。因此，學生實驗時鹽酸濃度應控制在0.02 mol·L-1以上，以降低實驗測量的誤差。雖然采用鎘電極會完全消除這個誤差，但是考慮到有效降低學生實驗產生的有毒有害廢棄物的因素，且采用銅電極獲得的實驗結果與理論分析具有相同的、可重復的變化趨勢，我們仍然建議采用“銅電極+酸堿指示劑”體系進行實驗教學工作，同時建議結合綜合化學實驗課程或開放實驗課程中的電催化氧化實驗內容，引導學生對這一問題進行拓展性研究。

由上述數據分析方法得到氫離子的極限遷移數t0后，可以將其代入方程(9)中，結合方程(3)計算出遷移數t+與溶液濃度c的二分之一次方間的擬合曲線，并與實驗測量數據進行對比。圖3是三組平行實驗所得的t+vs.c1/2數據點及其對應的理論計算曲線，可以看出在數據測量范圍內，理論曲線與實驗數據的吻合度還是比較好的。雖然三組平行實驗數據之間存在一定誤差，但是結合圖2的曲線可以看出，每個實驗的t0vs.c關系和t+vs.c1/2關系是相互自洽的。

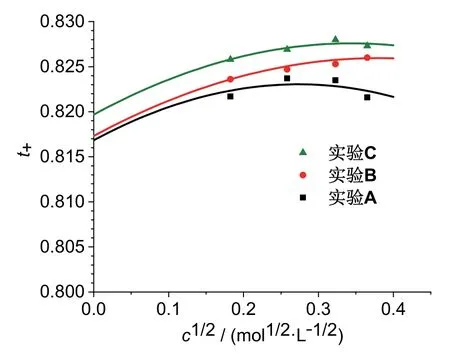
圖3 t+ vs. c1/2實驗數據及其理論計算曲線

3 討論和總結

實驗結果表明，通過測量一系列不同濃度鹽酸溶液的離子遷移數，是可以采用Longsworth外推方程獲得氫離子的極限遷移數的。如果將上述內容設計為教學實驗，大約需要8課時，基本滿足高年級本科生的專業實驗要求，與傳統的只進行單一濃度溶液遷移數測定的實驗設計相比，新的實驗教學內容具有如下優點：

(1) 雖然增加了實驗時長，但是獲得的實驗數據更多，對實驗數據的處理和計算內容更為豐富，比如利用方程(8)進行的線性擬合與外推，以及利用方程(9)進行的非線性擬合等，這對于培養學生的數據分析能力是有益的。同時，對一系列實驗數據的趨勢性分析能夠讓學生和教師對實驗結果的好壞有直觀的了解，這比簡單地對比文獻數據更有意義。

(2) 新的實驗設計有效關聯了電解質導電理論，使得物理化學理論教學內容在實驗課程中得到生動體現。但是可以注意到這樣一個事實，即經典的Debye-Hückel-Onsager電導率方程并不能在極限遷移數測量的問題上直接運用，而必須通過巧妙的實驗設計和數據分析方法，迂回達到目的。這首先說明了一個科學理論的應用實際上是有邊界的，當實踐過程在理論邊界之外時，往往會導致結果的不確定性(見圖1)；其次，因為極限條件下(本實驗為無限稀釋的溶液)的數據是很難測量的，新的實驗設計還可以向學生展示科學知識如何來源于實驗的問題。

(3) 新的實驗設計還很好地詮釋了化學應該如何看待和應用數學的問題。從方程(1)到方程(6)都是非常精彩的數學分析過程，但是對于解決極限遷移數的測量問題完全不起作用，解決這個問題依靠的是Longsworth提出的方程(8)，這實際上應該說是一種“化學直覺”。也就是說，當我們在應用物理學理論和數學方法把化學問題精確化的同時，必須首先依靠從實驗獲得的“化學直覺”，因為一切的化學知識實際上都來源于實驗。

綜上所述，除個別物理學常數測量內容外，在一個物理化學實驗項目中僅測定單一參數的教學設計并不十分可取，但是在國內高校的物理化學實驗教學中，這一類的實驗設計還是比較常見的，比如經典的燃燒熱測量實驗等，在這方面，我們與國際先進的物理化學實驗教學水平還有不少差距[16]要進一步努力。