斜入射地震下預制拼裝管廊地震響應分析

夏樟華，唐永波，林友勤，許有勝

（1.福州大學土木工程學院，福建福州 350108；2.深圳市市政設計研究院有限公司，廣東深圳 518035）

引言

地下綜合管廊，又稱共同溝，是將燃氣、電力、電信、給排水等2 種或2 種以上的生命線工程設施共同敷設于其中的地下結構［1］。發展建設地下綜合管廊已成為現代城市可持續發展的重要方向，而地下綜合管廊抗震性能研究具有重要的理論和現實意義［2］。早期日本學者Kawashima、高田至郎等［3－4］就討論了綜合管廊等地下結構在地震下反應的問題和土層液化下綜合管廊的破壞機理并給出了對應的整治措施。近些年來我國學者也開展了相關研究，岳慶霞［5］研究了地下結構地震波的輸入形式，通過對比得出較為精確的位移輸入方式；史曉軍等［6－8］開展了地下綜合管廊大型振動臺試驗研究，介紹了試驗方法、試驗結果以及數值模擬；馮瑞成［9］開展了共同溝模型試驗并進行了抗震性能的評價；黃臣瑞［10］采用數值模擬方式，指出縱向接頭彎曲剛度和軸向剛度是影響結果的關鍵因素以及行波激勵顯著增大了預制管廊的地震響應；梁建文等［11］研究了地下T 型交叉管廊的地震響應，指出T 型交叉管廊的交界面內力最大；此外，楊仕升等［12］針對管廊的典型節點進行了抗震研究，得出管廊節點在地震下具有良好的整體性，節點隔板與底板及中板、側壁與底板及中板為管廊的薄弱部位。可見，常規垂直入射下地下結構響應分析已較為成熟。

實際地震動在傳播中存在非一致性，通常假定處于工程近場處深源地震是以垂直基巖形式入射的平面體波，而處于工程遠場處的淺源地震系以一定的角度傳播至近場，即斜入射。斜入射相較于垂直入射由于行波效應存在著更為復雜的波場疊加情況，對于管廊等地下結構，斜入射地震作用下存在著更為復雜的響應。同時實際工程也表明，斜入射SV波相較于斜入射P波具有更大的破壞性，因此建立SV波斜入射的地震輸入方法并運用于實際工程進行地震響應的研究是有必要的［13－14］。目前國內外學者對于綜合管廊的地震響應分析大多數基于垂直入射的假定，對于斜入射地震波下管廊的地震響應較少。文中基于粘彈性邊界時域波動方法，闡述在三維空間下SV波沿一定角度入射的地震輸入方式，同時結合Auto_VSB輔助程序實現斜入射地震節點力的轉化，最后基于該地震輸入方法對預制節段拼裝綜合管廊進行地震響應研究。

1 預制拼裝管廊有限元建模分析

1.1 背景工程

以某試驗區環湖路綜合管廊工程為背景，綜合管廊截面采用單倉結構形式，標準段管廊斷面大小為3.9 m×4.1 m，頂底板及腹板壁厚35 cm。管廊標準段結構如圖1所示。

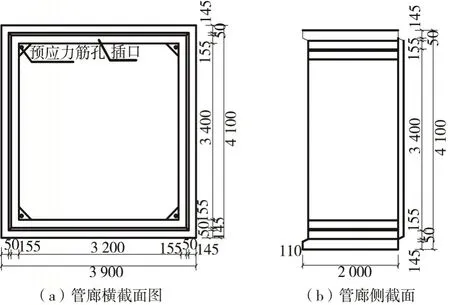
圖1 管廊截面圖Fig.1 Sectional view of utility tunnels（Unit：cm）

1.2 整體有限元模型

有限元模型是基于ABAQUS 平臺建立的三維實體模型［15］，土體、結構均采用實體模型C3D8R 進行模擬，鋼筋及預應力鋼絞線均采用TRUSS單元進行模擬，兩端采用MPC 約束進行端點耦合，并通過初始應力法來施加預應力，其中預應力根據工程實際取150 kN。在進行地下結構抗震數值分析時，土 體模型的長度截取十分重要，由于文中模型采用粘彈性邊界，有效地削弱了邊界對計算結果的影響，并模擬了遠域土體的特性，故近場土體的截取可適當縮小尺寸。因此在土體的截取采取如下原則：管廊結構左右兩側距離土體邊界均需大于3 倍管廊寬度，管廊結構底部距離基巖面需大于3 倍管廊高度，縱向長度取6 節管廊長度即12 m。綜上所述，土體模型尺寸為28 m×12 m×20 m，整體有限元模型及管廊精細模型如圖2及圖3所示。

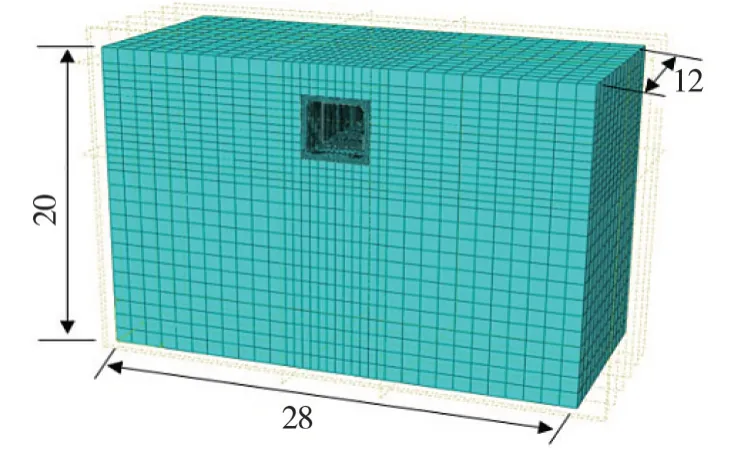
圖2 整體有限元模型Fig.2 Overall finite element model（Unit：cm）

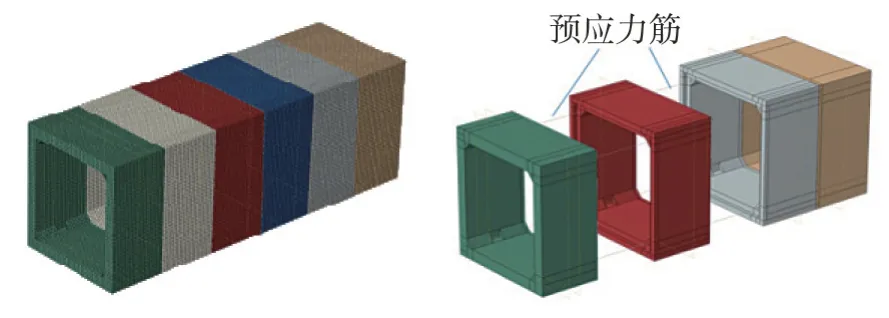
圖3 管廊有限元模型Fig.3 Finite element model of utility tunnels

1.3 土體動力特性本構

在地下結構的抗震分析中可采用非線性和等效線性動粘彈性模型來模擬土體本構2種方式。由于非線性本構所需的計算參數較為復雜，且計算耗費時長較長，等效線性方法可以通過不斷迭代逼近來反應土體非彈性與非線性以取得預期效果，該方式計算高效，且在地震加速度小于0.4 g 的情況下能提供較為合理的結果。故文中采用等效線性動粘彈性模型來模擬土體本構。

在ABAQUS 中沒有自帶等效線性本構，需要通過UMAT 用戶子程序進行編寫導入。UMAT 用戶子程序系采用FORTRAN 語言編寫，用戶需提供材料積分點雅克比矩陣以完成本構關系的開發。在文中采用UMAT用戶子程序的過程如下：

（1）通過*initial conditions，type=solution 導入各單元有效應力，作為狀態變量STATEV（1），在后續分析中供UMAT子程序調用；

（2）在UMAT子程序中將單元最大剪應變存儲為STATEV（2）；

（3）通過編寫的FORTRAN 語言將根據應變水平確定的等效剪切模量和等效阻尼比存儲為狀態變量STATEV（3）和STATEV（4）；

（4）最后將4個狀態變量作為初始變量替換第一步中*initial conditions，type=solution 導入的變量來完成迭代計算。

1.4 動力接觸分析

在基于SSI（soil-structure interaction）效應下的地下結構動力計算中，接觸作用扮演著至關重要的角色。動力接觸問題是一個高度復雜的力學不連續性問題，在非線性問題求解中，每次增量分析都須判斷接觸面的接觸狀態，進而不斷連續迭代的過程。目前常用的動力接觸數值算法有Lagrange 乘子法、修正Lagrange 乘子法、罰函數法和線性補償法。文中管廊結構與土體接觸采用面面接觸，并采用罰函數法進行求解。

1.5 地震波的選擇

由地勘資料可知，本工程擬建場地抗震設防烈度為7 度，基本地震加速度值為0.10 g，設計分組為第三組，場地類別屬Ⅱ類區段，反應譜特征周期為0.45 s。結合《建筑工程抗震性態設計通則》推薦［16］，主要采用Kobe 波對預制節段拼裝綜合管廊進行抗震分析，同時根據《GBT 51336－2018 地下結構抗震設計標準》［17］，并根據相應的分析需要對該組地震波進行加速度幅值調整，分別調整為0.1、0.2、0.3 g。

加速度幅值調整具體公式如下：

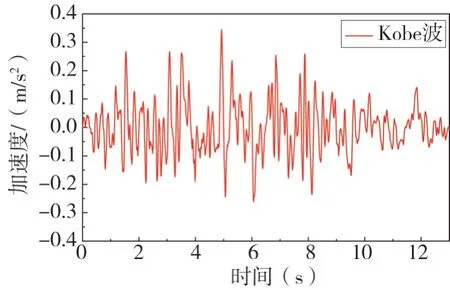
圖4 Kobe波加速度時程曲線Fig.4 Kobe wave acceleration time history curve

1.6 阻尼理論

在結構的動力分析中，阻尼的作用不容忽視，阻尼根據生成原因分為內阻尼和外阻尼。阻尼的存在能夠使結構的振動衰減以及能量耗散，對于結構的抗震起著有利的作用，目前ABAQUS 常用的阻尼有直接模態阻尼、瑞利阻尼、復合模態阻尼和結構阻尼，文中采用瑞利阻尼進行阻尼模擬。莊海洋［18］認為土體的非線性計算分析中，只需考慮土體材料的粘性效應，按瑞利計算，通常土體阻尼比取2%；混凝土阻尼比為5%。

1.7 土結共同作用動力方程及求解

結構動力平衡方程與靜力平衡方程類似，區別在于動力平衡方程需在單元中考慮阻尼以及慣性力的影響。

在結構物未形成前，自由場情況下土－基巖運動方程：

式中：UC是自由場位移向量；Mf是自由場質量矩陣；Kf、Cf分別為對應的剛度矩陣及阻尼矩陣；{Pe（t）}為有效地震力。

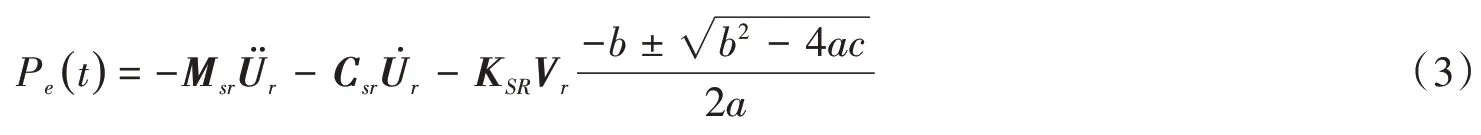
當結構物形成時，土－結構體系運動方程如下：

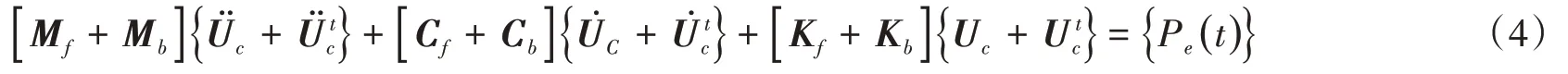
式中：Mb、Cb、Kb分別為結構物的質量矩陣、阻尼矩陣、剛度矩陣；Ut c表示結構物產生的反作用運動。

動力平衡方程的求解方法包括振型疊加法、復反應分析法和逐步積分法。ABAQUS 隱式動力計算采用的是逐步積分法中的Newmark-β法，為求解非線性問題提供一個良好穩定的平臺。

2 粘彈性人工邊界及Auto_VSB輔助程序

2.1 場地土模擬的邊界問題

在進行地下結構動力分析時，目前常用的人工邊界分2 類，一類是全局邊界，另一類是局部人工。雖然前者具有高精度的特點，但方程的耦合性使其在求解硬件上要求較高，適用性上有較大的局限性；目前常用的局部人工邊界有黏性邊界、透射邊界、粘彈性邊界［19－20］。文中所采用的是局部人工邊界中的粘彈性邊界。

2.2 粘彈性邊界的設置

集中粘彈性人工邊界的具體實現方法是在邊界處離散分布彈簧和阻尼器，分別用來模擬邊界遠域處彈性恢復性能和抵消散射波在邊界處的反射效應，在ABAQUS 隱式算法中采用Springs和Dashpots來實現彈簧和阻尼器的添加，即在邊界節點處使用Springs和Dashpots代替傳統靜力邊界，完成動力邊界的建立。

三維粘彈性人工邊界（見圖5）系在球面坐標上進行推導，忽略波的匯聚性僅考慮剪切波在球面上擴散時，設切斷截面r=R，則其三維粘彈性人工邊界的彈簧剛度及阻尼系數由式（5）和式（6）確定，

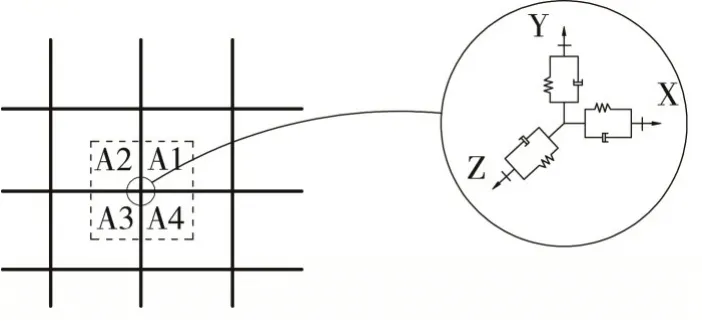
圖5 三維粘彈性邊界示意圖Fig.5 Schematic diagram of three-dimensional viscoelastic boundary

式中：KT和CT人工邊界上切向彈簧剛度和阻尼系數；KN和CN分別為法向彈簧剛度和法向阻尼系數G 為剪切模量；R為切斷面半徑；ρ為地基質量密度；Cs和Cp分別為S波和P波波速。

2.3 三維粘彈性人工邊界等效節點力的轉化

施加粘彈性邊界后，預設外傳散射波被邊界完全吸收，此時若是直接在基底施加位移時程，則將產生波的反射，即在邊界處產生彈簧阻尼反力，故采取的方法是將外源地震動轉化為等效節點力，同時抵消彈簧阻尼反力，現以三維邊界為例，等效節點力可用下式進行計算。

式中：Kb和Cb分別為彈簧剛度及阻尼系數對角矩陣分別為自由場位移向量、速度向量以及應力張量；Ab為邊界節點影響面積。

2.4 斜入射人工邊界內行場位移

同垂直入射粘彈性人工邊界，采用方形邊界替代球形邊界以更貼近實際工程，圖6 為三維平面SV 波斜入射示意圖，并假設SV 波波陣面平行于人工邊界地面的一條棱。由圖6 可得出邊界面上各點的內行場情況，其中前后邊界及左邊界的內行場構成為斜入射的SV 波和地面反射的SV 波及P 波，屬于自由場；底面邊界的內行場的構成僅為斜入射的SV 波；右面邊界無內行場［21］。

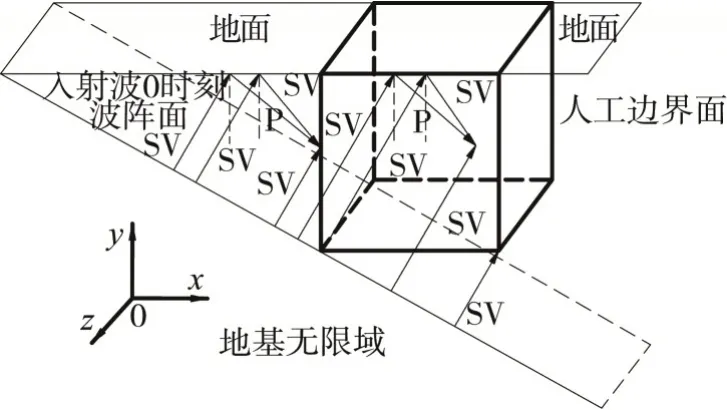
圖6 三維平面SV波斜入射示意圖Fig.6 Schematic diagram of three-dimensional plane SV wave oblique incidence

考慮斜入射傳播非一致性的特點，地震波傳播到各個位置的過程存在著時間差，則左側邊界的內行場中的入射角為α的SV波、反射角為α的SV波及反射角為β的P波時程分別為u0(t-Δt1)、A3u0(t-Δt2)A4u0(t-Δt3)則左側邊界內行場位移為：

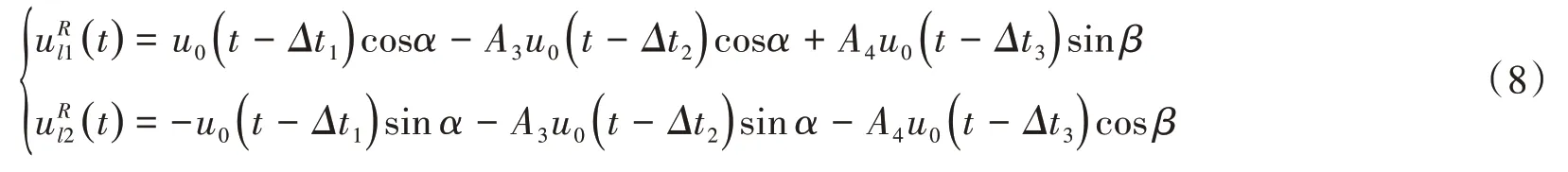
前后邊界的內行場中的入射角為α的SV 波、反射角為α的SV 波及反射角為β的P 波時程分別為u0(t-Δt4)、A3u0(t-Δt5)、A4u0(t-Δt6)，則前后邊界內行場位移為：

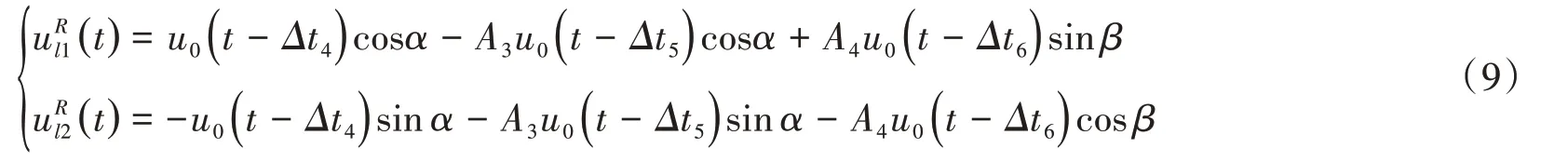
底邊邊界的內行場僅存在著時程為u0(t-Δt7)的入射角為α的SV波，則底邊內行場位移為：

式中：A3為反射SV 波與入射SV 波幅值的比值；A4為反射P波與入射SV 波的幅值的比值；u0(t)為入射波位移時程，各邊界面上的y方向位移u均為0；Δt1-Δt7分別為左側邊界的直接入射SV波、地表反射SV波、地表反射P波和前后邊界的直接入射SV波、地表反射SV波、地表反射P波及底邊界相對于入射波u0(t)初始時刻的延遲時間，可由式（11）計算而得：

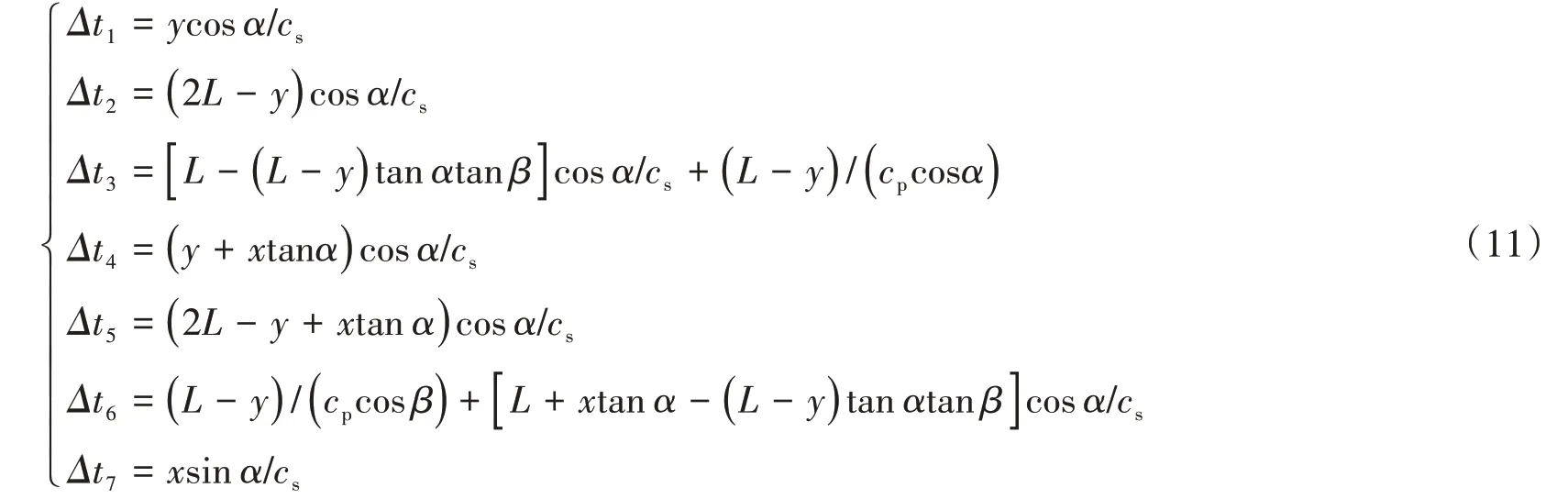
式中：左側邊界結點的坐標為（0，y）；底邊界結點的坐標為（x，0）；L為左邊界的高度。

2.5 斜入射人工邊界內行場應力

當已知各邊界內行位移場便可推導出內行應力場。

其中左側邊界應力場為：

前側人工邊界應力場為：

后側人工邊界應力恰好與前側應力相反。底部邊界應力場為：

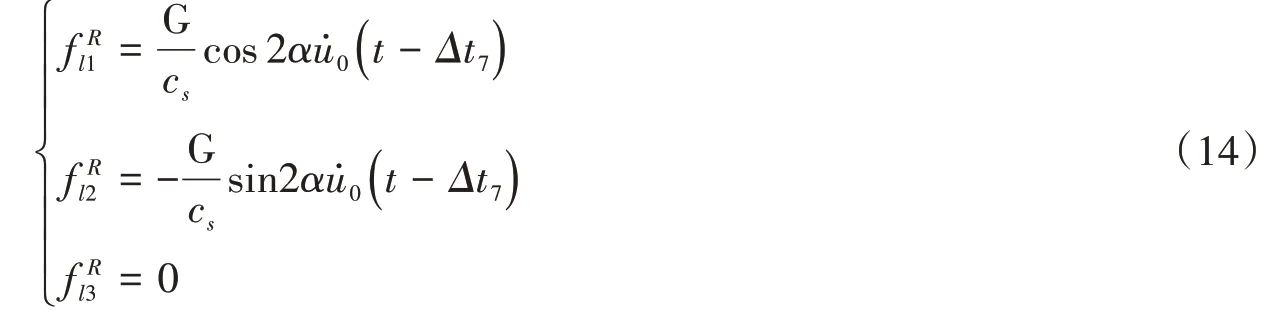
式中：CP和CS分別為P波和SV波的波速；λ和G為拉梅常數。

2.6 基于python語言的粘彈性人工邊界輔助程序Auto_VSB

根據上述分析，只要已知節點控制面積以及外源波位移時程和速度時程，便可以求得等效點力，然后通過ABAQUS 的*Cload 和*Amplitude 來實現節點力的輸入，但是由于模型體量巨大，節點眾多，無論是節點力的求取還是施加都是一個復雜且浩大的工程，重復率高且容錯率低，傳統的計算方式是結合Matlab 編制簡單的計算程序，再通過一系列復雜的程序完成。值得一提的是Matlab 是基于矩陣計算的程序語言，轉換效率較為緩慢，一個地震波工況的轉換通常耗時10～20 min，在非線性計算中效率極低。文中結合上述需求基于python 編程語言，編制了粘彈性人工邊界及節點力自動施加程序Auto_VSB（Automatic Viscous-Spring Boundary）。所編制的Auto_VSB輔助程序擁有簡單的操作界面（如圖7），用戶僅需輸入一些簡單的場地物理條件，包括坐標、彈性模量等參數，結合用戶放入的任意地震波位移時程及速度時程等文件，即可實現粘彈性邊界及節點力文件的快速生成。每條地震波轉換耗時僅需要3 s，極大地提高了效率。

圖7 Auto_VSB程序界面Fig.7 Auto_VSB program interface

2.7 基于Auto_VSB輔助程序的斜入射地震輸入的精度驗證

基于以上地震力輸入方法，將斜入射節點力自動計算功能內置于Auto_VSB 輔助程序中，為了驗證該程序所建立的斜入射方法精度，建立長×寬×高為400 m×400 m×600 m三維土體，離散單元網格為20 m×20 m×20 m，土體彈性模量E=4.88 GPa，密度ρ=2 000 kg/m3，泊松比ν=0.22，外源波步長取0.01 s，歷時2 s，分別以入射角為15°和30°入射SV波脈沖，脈沖方程式為：

式中：μ為位移；t為時間。

圖8為施加了粘彈性邊界及斜入射節點地震力幅值的驗證模型圖，由于地震力由左側入射，故右側不存在節點力幅值。圖9 是入射角為15°和30°下的驗證模型應力云圖。圖10 為入射角為15°和30°時驗證模型底部中點和頂部中點位移時程圖。可以看出斜入射輸入方式隨著入射角度的變化會產生不同的結果，疊加規律較為復雜，由于斜入射波從左下角入射，傳播至頂部中點及底部中點均需時間，故底部中點位移時程不是從0 s開始，且頂部中點位移時程與底部位移時程存在時間差延遲，兩種不同角度的入射波折射反射的疊加方式不同，但最終波都由邊界吸收歸為0。

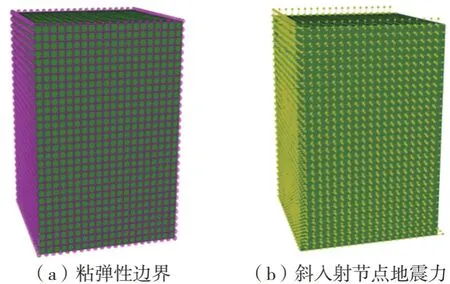
圖8 斜入射地震波下粘彈性邊界驗證模型Fig.8 Validation model of viscoelastic boundary under obliquely incident seismic waves

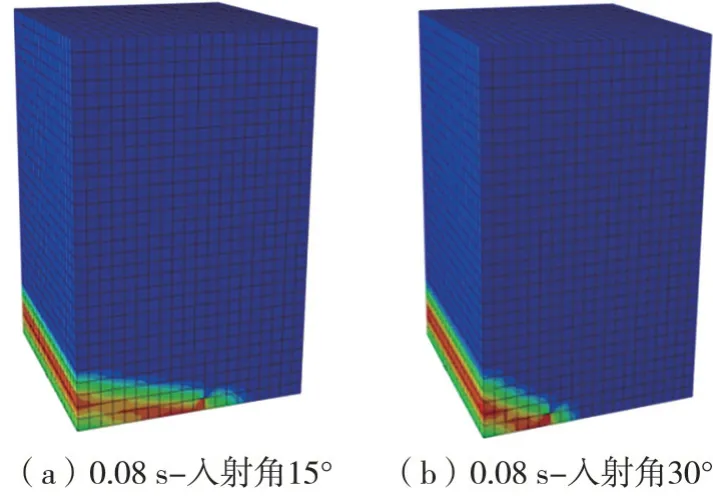
圖9 0.08 s時入射角15°和30°模型應力云圖Fig.9 Stress cloud diagram of the model with an incident angle of 15°and 30°at 0.08 s

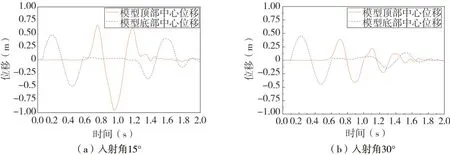
圖10 入射角15°和30°底部中點和頂部中點位移時程圖Fig.10 Time history diagram of the displacement of the bottom midpoint and the top midpoint at 15°and 30°incident angles

3 斜入射管廊的動力計算結果分析

斜入射地震作用下具有復雜的行波效應，結構在行波效應的作用下應變有所增大［22］。采用不同入射角度的方法以此來考慮行波的效應。將Kobe 地震波調整為0.1 g 并采用3 種入射角度由模型左下角輸入進行對比分析，角度分別為0°、15°、30°，圖11為3種不同入射角度下整體模型應力云圖。

圖11 3種不同入射角度地震力路徑圖Fig.11 Seismic force path diagrams under three different incident angle

分別對結構施加入射角為0°、15°、30°的地震波，測出管廊底部及土體底部加速度、側壁相對水平位移、接頭橫向錯動位移以及豎向接頭位移。以下僅列出入射角為30°時的測量結果，圖12為入射角為30°時的土體及管廊底部加速度時程曲線圖，圖13 為側壁相對水平位移，圖14 為管廊第一主應力與第三主應力云圖，圖15為接頭的錯動位移時程圖。綜合分析得出：

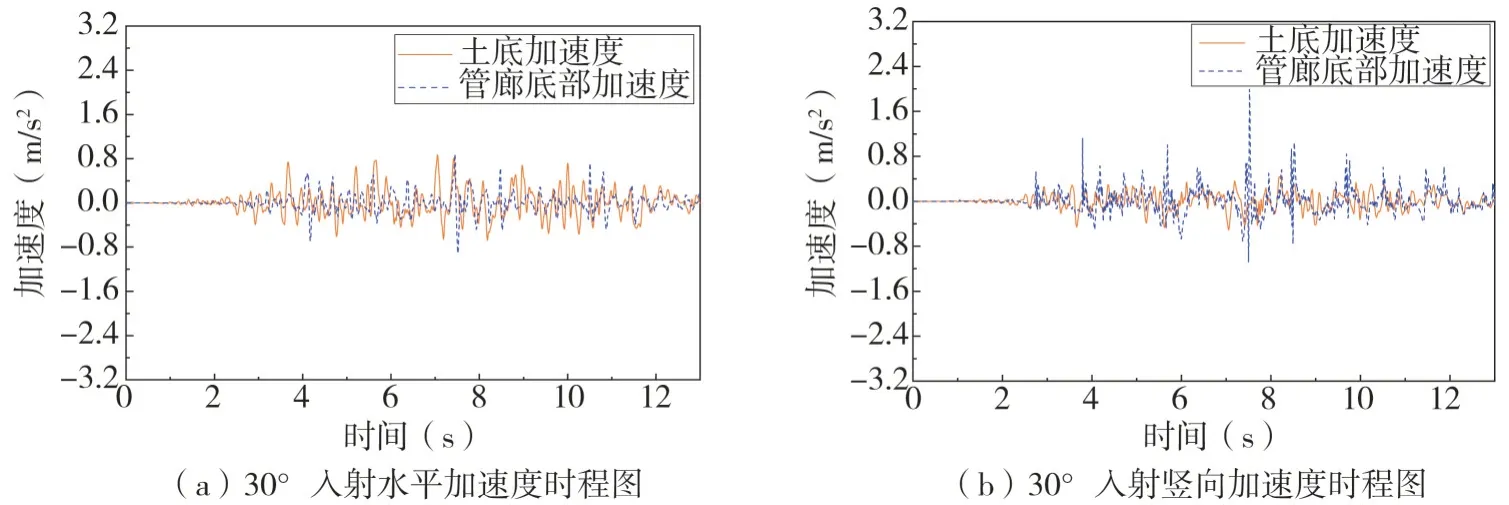
圖12 入射角為30°地震作用下管廊底部及土體底部加速度時程曲線Fig.12 Acceleration time history curve of the bottom of the utility tunnels and the bottom of the soil under the earthquake action of an incident angle of 30°

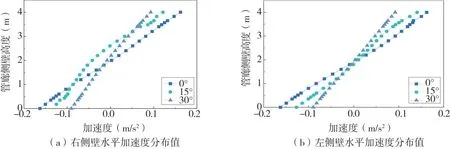
圖13 管廊側壁水平加速度分布值Fig.13 Horizontal acceleration distribution value of the side wall of the utility tunnels

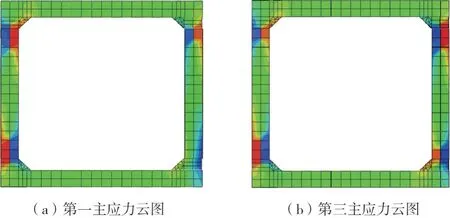
圖14 30°入射下第一主應力與第三主應力云圖Fig.14 Contours of the first and the third principal stresses at 30°incidence

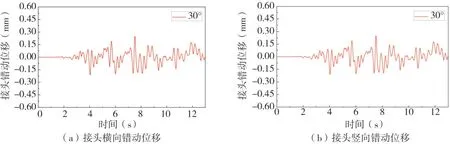
圖15 30°入射地震波作用下接頭錯動位移時程圖Fig.15 Time-history diagram of joint displacement under 30°incident seismic waves

（1）斜入射地震波輸入時會分解為水平和豎向2 個分量。其中，入射角為30°時，水平加速度放大系數為1.01，豎向加速度放大系數為4.41；入射角為15°時放大系數分別為1.12和1.56；入射角為0°時放大系數分別為1.89 和0。可以發現，與垂直入射相比，由于反射折射復雜疊加的作用影響，土底加速度傳播至結構底部會被放大，且隨著入射角度的增加，水平加速度放大系數逐漸減小，而豎向加速度放大系數隨著角度的增加逐漸增大，且放大系數明顯大于水平加速度的放大系數。

（2）隨著入射角度的增大，同一高度管廊側壁水平加速度逐漸減小，管廊高度為0.5 m時，水平加速度由入射角為0°時的0.15 m/s2減小到15°時的0.1 m/s2再減小到30°時0.075 m/s2，大致以側壁中點為正負加速度分界點，這也將造成結構頂底板相對水平位移的產生。

（3）在斜入射地震作用下，管廊結構依然在腋角四周應力分布較為集中。隨著角度的增加，結構的第一主應力逐漸減小，第三主應力逐漸增大，造成該原因主要是因為豎向分量的增加及波發生反射折射疊加造成。其中在0°入射條件時第一主應力最大，為322 kPa，在30°入射條件時第三主應力最大，為－412 kPa。因為斜入射在豎向的作用上會比垂直入射方式來的大，這也是由于角度的增大引起豎向加速度放大導致的，需要引起一定的重視。

（4）隨著入射角度的增大，結構接頭間橫向錯動位移不斷減小，豎向錯動位移不斷增大，入射角為0°、15°、30°時橫向接頭位移分別為0.37、0.25、0.22 mm；入射角為15°、30°豎向接頭位移分別為0.25、0.28 mm。可以發現豎向位移的增大大于水平位移的減小，對接頭的影響明顯增大。

4 結論

（1）在對單元選擇、土體動力本構、動力接觸模擬和求解方法分析的基礎上，建立了考慮土結共同作用的預制拼裝綜合管廊的動力分析有限元模型。通過分析斜入射的內行位移場及應力場，建立了考慮斜入射粘彈性邊界，能夠實現斜入射地震作用下預制拼裝管廊的地震響應分析，基于Python 編程語言所編制的粘彈性人工邊界及節點力自動施加程序Auto_VSB能夠極大提高計算效率且具有很好的計算精度。

（2）與垂直入射相比，由于反射折射復雜疊加的作用影響，斜入射時土底加速度傳播至結構底部會被放大，且隨著入射角度的增加，水平加速度放大系數逐漸減小，而豎向加速度放大系數隨著角度的增加逐漸增大，且放大系數明顯大于水平加速度的放大系數。其中，入射角為30°時，水平加速度放大系數為1.01，豎向加速度放大系數為4.41。

（3）隨著入射角度的增大，同一高度管廊側壁水平加速度逐漸減小，大致以側壁中點為正負加速度分界點，這是造成結構頂底板相對水平位移產生愿原因。

（4）隨著入射角度的增大，結構接頭間橫向錯動位移不斷減小，豎向錯動位移不斷增大，可以發現豎向位移的增大大于水平位移的減小。說明，斜入射輸入方式在豎向對結構造成較大影響，且總體變形明顯大于水平入射，在實際工程中應加以考慮。