基于磁流變阻尼器的結構仿人智能控制方法研究
李振東
(中鐵第四勘察設計院集團有限公司,湖北武漢 430063)
引言
在土木工程領域,控制技術廣泛用于減輕動力作用危害以及提高結構在地震等外部作用下的抗震性能。半主動控制由于既具有被動控制的可靠性又保留了主動控制的多功能性和適應性而備受國內外學者關注[1]。磁流變(magnetorheological,MR)阻尼器是一種重要的半主動控制裝置,其為一種基于磁流變液的可控阻尼器。磁流變液[2]是一種兩相懸浮的智能驅動材料,在磁場作用下能在0.01 s 的瞬間由牛頓流體變成粘塑性體或反之,MR阻尼器通過調節磁化電流來控制此粘塑性體的屈服剪切應力,并且對電源具有非常低的功率要求,這對于在地震期間可能造成大功率設備主供電源被切斷顯得尤為重要。近年來,基于MR阻尼器的半主動控制越來越多的受到人們的關注[3,4]。
迄今為止,國內外學者開發了許多有效的半主動控制方法,通常將它們分為2 類:基于模型的控制和基于軟計算的智能控制。基于模型的控制,如線性最優控制[5-7]、瞬時最優控制[5-6]、線性二次型(LQR)最優控制[1,8]、線性二次型高斯(LQG)最優控制[1,6]、滑模控制[9]等。歐進萍等[8]提出了基于MR 阻尼器的海洋平臺LQR 最優控制系統,可以有效降低平臺結構位移和甲板加速度響應。Dyke 等[1]提出了剪切最優控制器(COC)用于將理想的控制力轉化為MR 阻尼器的控制電壓,采用COC 和H2/LQG 控制方法對設有MR 阻尼器的3層框架進行仿真研究,結果表明半主動控制能有效降低結構動力響應。Lee等[9]研究對比了滑模控制與2種被動控制的減隔震效果,研究表明滑模控制在減低橋梁位移響應方面優于2種被動控制。基于模型的控制方法,控制目標和增益矩陣的選擇是一個相對不確定的因素,需要依靠設計者的經驗,選擇不合理可能會影響最終的控制效果。神經網絡控制[10-12](NNC)、模糊邏輯控制(FLC)[13-15]、智能優化算法控制(IOAC)[16]以及三者的相互結合構成了類型多樣的智能控制。Wang等[12]研究提出了一種神經網絡控制方法,設計了MR阻尼器逆模式神經網絡和用于預測下一時刻MR阻尼器驅動電流的神經網絡。Choi等[13]設計了一種模糊邏輯控制器,用于降低MR 阻尼結構的地震響應。Yan等[16]提出了一種遺傳自適應模糊控制,將控制目標轉化為適應度函數,用于設有MR阻尼器的結構在地震載荷作用下振動控制,通過仿真研究證明了該方法在減低結構動力響應方面的有效性。但是,智能控制也存在一些問題,如神經網絡控制在網絡結構的選擇、訓練集的選取、網絡的穩定性等方面的研究尚不夠深入。一般地,智能控制系統設計困難、實現過程復雜,往往對控制計算機的硬件設施要求很高,有時需要依賴特定的開發平臺,這使結構控制實施難度加大。
針對以上現狀,本研究提出了一種仿人智能PID控制策略,并應用于一個磁流變阻尼結構的振動控制系統。這種控制算法可以根據輸入信息來識別被控系統所處的狀態、動態特征及行為,并模仿人的智能控制決策行為實現對系統的智能控制。該算法構造簡單,很好地解決了控制過程中的快速性、穩定性和準確性的矛盾。通過仿真分析,驗證了仿人智能PID算法在結構振動控制應用中的可行性和有效性。
1 MR阻尼器的力學特性試驗和建模
試驗阻尼器主筒直徑150 mm,設計行程±80 mm,最大出力100 kN。試驗測試系統如圖1 所示,采用頻率為0.15 Hz,振幅為±7 cm 的正弦激勵,控制信號電壓采用恒定電壓:0、1.5、2.4、3.3、4.5、6.0 V,對應的磁化電流分別為0、1.5、2.4、3.3、4.5、6.0 A,MR 阻尼器的響應結果如圖2 所示。

圖1 試驗測試系統Fig.1 Experimental test system
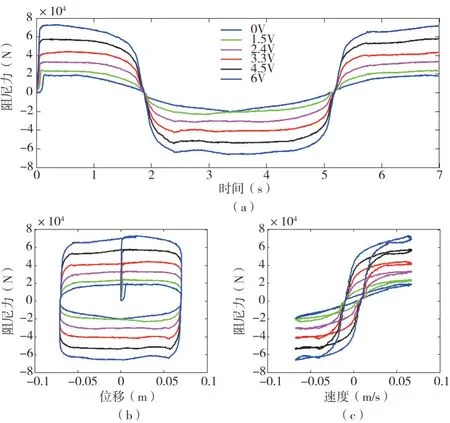
圖2 MR阻尼器試驗曲線Fig.2 Test result curve of MR damper
Spencer現象模型[1]被廣泛應用于描述MR阻尼器的力學特性,該模型組成如圖3 所示。MR 阻尼器的阻尼力f可通過下式確定:
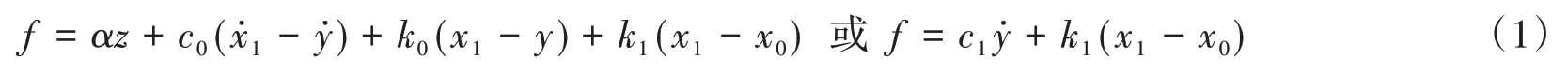
式中:x1為活塞的相對位移;z為演化變量,可通過式(2)和式(3)確定:
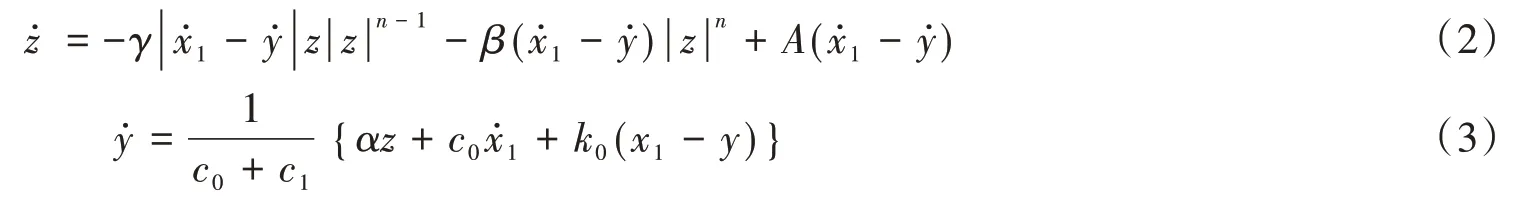
式中:k0、k1、c0、c1為圖3中結構的相關特性參數;x0為剛度為k1彈簧的初始位移;γ、β、A的調整可以控制MR阻尼器滯回曲線的形狀。

圖3 MR阻尼器的力學模型Fig.3 Mechanical model of MR damper
控制信號電壓通過影響參數α、c0、c1的取值來影響MR阻尼器的阻尼力f,為了確定適用于波動磁場的綜合模型,參數α、c0、c1被定義為有效電壓u的線性函數,如下:

為模擬MR 阻尼器中磁流變液達到流變平衡所涉及的動力學特性,采用如下一階濾波器來計算有效電壓u:

式中:ν為輸入的控制電壓信號;u為濾波器的輸出;η用于反映MR阻尼器在電流驅動時電磁鐵的動力特性。
式(1)~式(7)共包含了14個參數,利用MATLAB優化工具箱對模型的參數進行識別[17],由于參數η的識別需要引入MR 阻尼器變電壓控制試驗,試驗條件限制的原因,這里假設η取180 s-1。MR 阻尼器參數識別結果見表1,圖4為試驗與模擬結果的比較。結果表明,Spencer模型能夠較好地反映MR阻尼器的力學特性。
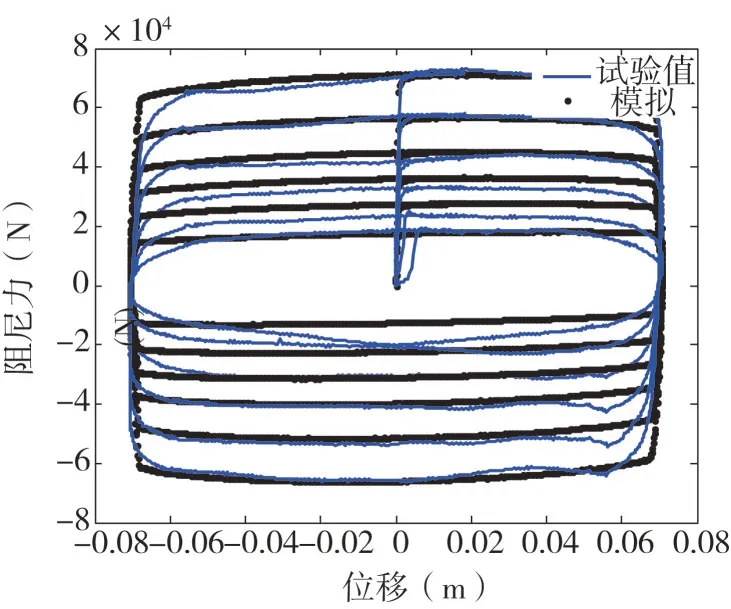
圖4 MR阻尼器試驗與模擬結果比較Fig.4 Comparison of experimental and simulation results of MR damper
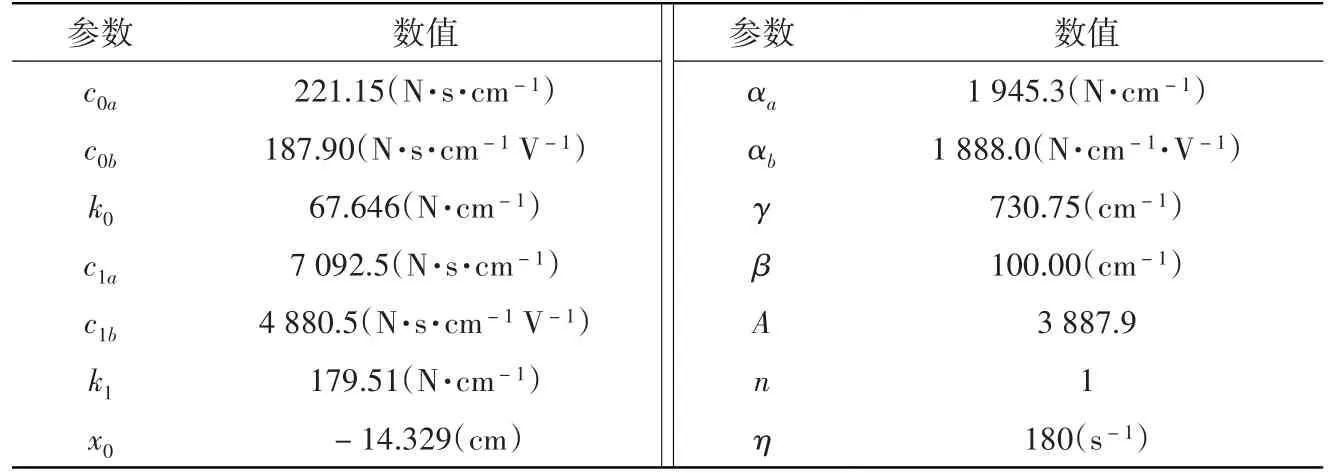
表1 MR阻尼器力學模型的參數表Table 1 Parameters of MR damper mechanical model
2 基于MR阻尼器的PID控制方法
常規PID 控制將系統受控量與目標值之差e的比例、積分和微分的線性組合作為控制量對受控對象實施控制,基于MR 阻尼器的PID 控制系統如圖5 所示,通過調整PID 控制的比例系數(Kp)、積分系數(Ki)和微分系數(Kd)能夠獲得比較滿意的控制效果。
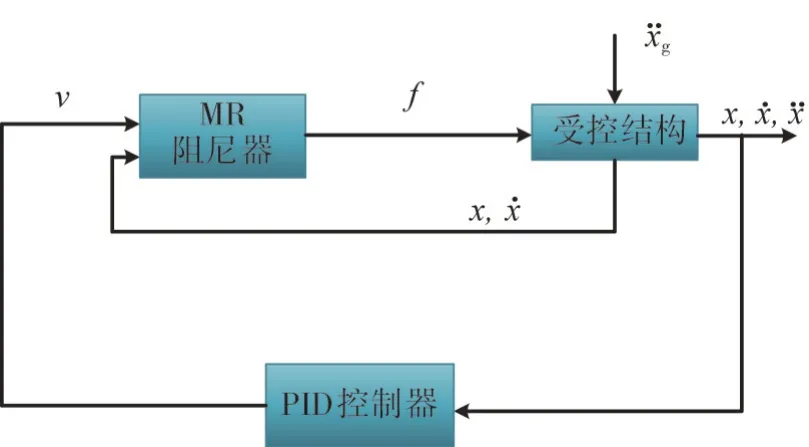
圖5 PID控制系統框圖Fig.5 The PID control system block diagram
在控制系統中,PID控制器的離散化表示形式為:
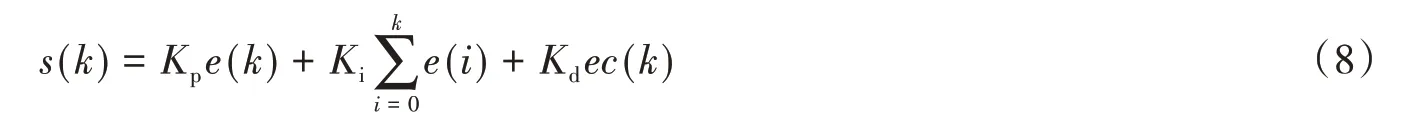
式中:s(k)為控制器第k個時刻輸出;e(k)控制器第k個時刻誤差值;ec(k)為第k個時刻誤差的微分。
3 基于MR阻尼器的結構仿人智能PID控制方法
3.1 仿人智能PID控制基本原理
仿人智能PID控制將常規PID控制與專家控制相結合,根據受控結構響應的動態特征及行為,借助專家控制經驗、啟發式直觀判斷和直覺推理規則來實現對結構的控制,以增強系統對不確定因素的適應性、魯棒性。為實現仿人智能控制,選用受控量與目標值之差e及其變化Δe作為仿人智能控制器的輸入信號,則輸出s表示為:

研究選擇結構的層間位移作為受控量,目標值設為0 m,誤差的變化Δe定義為當前時刻和前一時刻層間位移之差,特征變量e(k)·Δe(k)表征了層間位移的絕對值的變化趨勢,而控制器的輸出為MR阻尼器的控制電壓(0~6 V)。基于MR阻尼器的結構仿人智能控制系統如圖6所示。
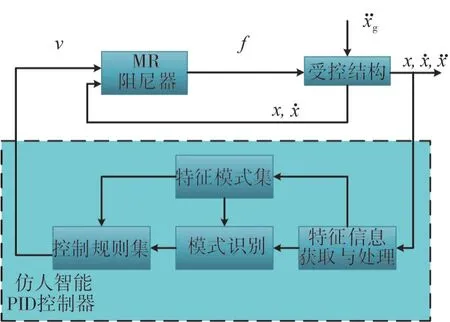
圖6 仿人智能PID控制系統框圖Fig.6 The humanoid intelligent PID control system block diagram
3.2 仿人智能控制算法
設e(k)表示當前采樣時刻的誤差值,e(k-1)和e(k-2)分別表示前一個和前兩個采樣時刻的誤差值,則有:

根據系統所處的狀態、相對位移絕對值變化情況以及是否處于極值對MR阻尼器采用不同的控制策略,如表2所示。

表2 MR阻尼器電壓控制策略Table 2 Voltage control strategy of MR damper
(1)當|e(k)|>M1時,對應狀態1,由于誤差的絕對值很大,此時不考慮誤差的變化趨勢,對系統實施開環控制,MR阻尼器采用Passive-on 控制,控制器按照控制電壓的上限輸出,即:s(k)=Umax;
(2)當e(k)·Δe(k)>0或Δe(k)=0時,對應狀態2,誤差在向絕對值增大的方向變化或誤差不發生變化,此時根據誤差絕對值|e(k)|的大小來實施控制,促使|e(k)|向減小的方向移動,|e(k)|較大時采用較強控制,較小時采用一般控制,控制器的輸出表示為:

(3)當e(k)·Δe(k)<0 且Δe(k)·Δe(k-1)<0 時,對應狀態3,誤差處于極值,同情形(2),可根據誤差絕對值|e(k)|的大小來實施控制,使|e(k)|能夠快速衰減,此時控制器的輸出表示為:
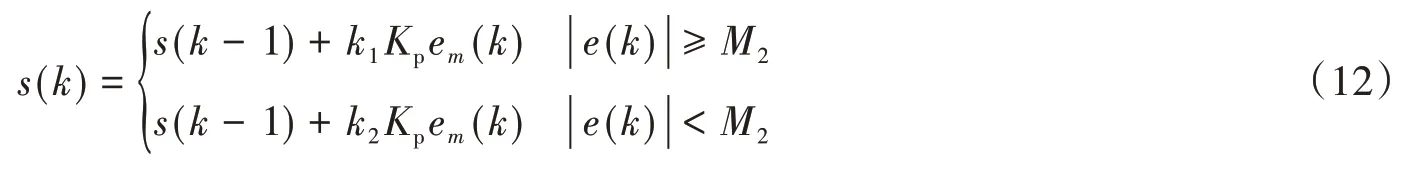
(4)當e(k)·Δe(k)<0 且Δe(k)·Δe(k-1)>0,或者e(k)=0 時,對應狀態4,誤差在向絕對值減小的方向變化或誤差達到平衡,此時保持控制器輸出不變,表示為:
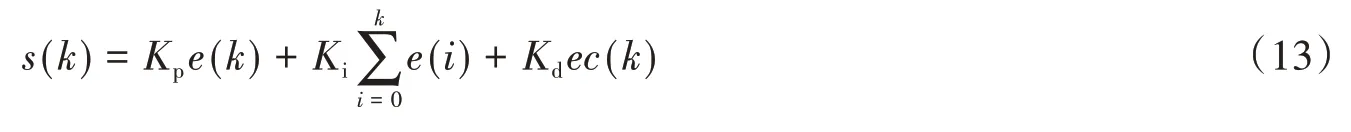
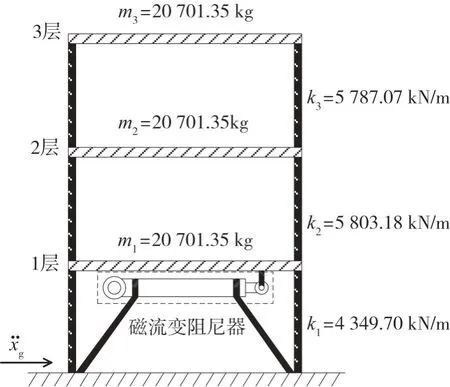
(5)當|e(k)| 上述控制算法中,s(k)、s(k-1)分別為控制器第k次和第k-1 次輸出;k1為放大系數,且k1>1;k2為抑制系數,且0 本節通過數值模擬來評估仿人智能PID 控制算法的性能。研究選取一個三層剪切型框架,其原型結構為Chung等[18]使用的振動臺試驗模型,如圖7所示。 圖7 三層框架模型Fig.7 Three-story frame structure model 地震作用下,結構的運動學方程為: 式中:m、k、c分別為結構質量矩陣、剛度矩陣和阻尼矩陣;f為MR 阻尼器阻尼力,由式(1)~式(7)確定;x=[x1,x2,x3]T為相對于地面的結構位移矢量;Γ=[ -1,0,0]T為MR阻尼器位置指示矩陣;Λ=[ 1,1,1]T為地震作用向量為地震地面運動加速度。 結構的質量矩陣m、剛度矩陣k分別為: 結構阻尼假設為Rayleigh阻尼,按下式確定: 式中,a0和a1分別為質量矩陣和剛度矩陣的組合系數,可按下式求解: 式中:ωm和ωn分別為結構的第m階和第n階自振頻率;ξm和ξn為相應于第m階和第n階振型的阻尼比。這里取m=1,n=2,解得結構自振頻率為ω1=6.845 8 rad/s,ω2=19.904 4 rad/s,設第1階和第2階振型的阻尼比ξ1=ξ2=0.02,則結構阻尼矩陣為: 將系統的運動方程寫入狀態空間,相應狀態方程可以表示為: 式中,狀態變量Z及矩陣A、B1、B2如下: 系統輸出狀態方程: 式中,輸出狀態向量Y及矩陣C、D1如下: 因此,結構的狀態空間模型可以表示為: 式中,u(t) =[(t),f(t)]T為仿真輸入向量;B=(B2B1);D=(0 D1)。 外部激勵選擇El Centro(NS,1940)波,加速度峰值為3 417 mm/s2,如圖8 所示。MR 阻尼器采用第1 節所建立的現象學模型模擬,增益設為2,以滿足控制力要求。在進行模擬時,將參數x0設定為0,以消除結果不對稱現象,使結構位移響應的穩態值為0。 圖8 El Centro 波Fig.8 El Centro wave 為證明所提控制方法的可行性和有效性,仿真考慮5種情況:無控、被動控制(0 V 和6 V)、常規PID 控制、仿人智能PID控制以及理想的主動控制。 常規PID 控制采用試湊法來確定參數的取值,在Kp取0.72、Ki取0、Kd取0.05,仿真可以得到較好的結果。對于仿人智能PID 控制,當層間位移小于h/1 000 時,采用Passiveoff,故考慮控制器的輸入為e/(h/1 000)。參數M1的取為4;M2取為2.5;M3取為1;k1取1.5;k2取0.5;Kp取0.02;Ki取0;Kd取0.001。為了控制仿人智能PID 控制器輸出,增設制約控制器輸出,確保MR 阻尼器輸入電壓為0~6 V。為比較主動與半主動控制系統,設計了理想的線性主動控制器[1],使其控制力與半主動控制力相近。理想的主動控制被認為是采用控制力能力相當的主動控制系統能達到的最好性能的控制策略。 表3 給出了結構在El Centro 波激勵下不同控制策略結構的響應峰值情況,圖9 和圖10 分別給出了在El Centro 波激勵下不同控制策略結構3層位移和絕對加速度時程曲線。 表3 El Centro 波激勵下不同控制策略結構的響應峰值Table 3 The peak structural response of different control strategies under El Centro wave excitation 圖9 El Centro 波激勵下不同控制策略結構3層位移時程曲線Fig.9 Displacement time-history curves of the third floor with different control strategies under El Centro wave excitation 圖10 El Centro 波激勵下不同控制策略結構3層加速度時程曲線Fig.10 Acceleration-time curves of the third floor with differ‐ent control strategies under El Centro wave 由表3 可以確定被動控制(Passive-off 和Passive-on)對3 層的相對位移控制效果為49.7%和58.8%、絕對加速度的控制效果為45.8%和30%、層間位移控制效果為45.6%和30%,可見被動控制具有一定的控制效果。同時注意到Passive-on 由于較大的阻尼力增加了頂層的層間位移以及頂層的加速度,這表明選擇能產生最大阻尼力的被動設備并不總能達到較好的控制效果,該結論可以直觀地從圖9 和圖10 反映。PID 控制和仿人智能PID控制由于具備對系統動態修正的特點,兩者較兩種被動控制模式均具有較好的控制效果,而仿人智能PID 控制具有更高的性能。雖然仿人智能PID 控制對1層的相對位移和絕對加速度的控制效果較Passive-on略差,但是對上層的相對位移、層間位移和絕對加速度控制效果均比兩種被動控制和PID控制好,說明基于MR阻尼器的仿人智能PID控制在建筑結構振動控制應用中的可行性和有效性。 為評估仿人智能PID控制的優越性,將其控制效果與理想的主動控制做比較,主動控制下結構的響應峰值見表3。從圖9 和圖10 中可以看出理想的主動控制對結構響應峰值的控制較好,尤其對加速度的控制十分有效。定量地分析,二者對3 層的相對位移控制效果為75.1%和72.9%、絕對加速度的控制效果為46.0%和54.0%、層間位移控制效果為46.1%和53.9%;對結構的最大層間位移控制效果為57.1%和67.9%。可見仿人智能PID 控制在降低頂層相對位移峰值方面的性能比線性主動控制略好,并且仿人智能PID 控制的最大層間位移要比主動控制的控制效果小10.8%,另外兩者的控制效果相差均小于10%,這一結果可能歸于MR阻尼器良好的適應性和穩定性以及仿人智能PID 算法的有效性。進一步分析二者對3 層的平均控制效果,發現對相對位移的控制相差0.84%,對絕對加速度的控制相差5.98%,二者十分接近。由此可知仿人智能PID控制可以達到甚至超過理想主動控制的性能,考慮到半主動控制具有非常低的功率要求,這一結果是相當顯著的。 為進一步評估仿人智能PID控制的有效性,另外選擇遷安波(NS,1976)作為外部激勵,調幅后加速度峰值為5 295.7 mm/s2,得到各種控制策略下結構響應峰值如圖11 所示。從圖中可以看出仿人智能PID 控制在減小結構動力響應方面效果較好,其在降低頂層相對位移峰值方面的性能尤為突出,并且可以有效控制結構的加速度響應。值得注意的是,在進行仿真時,未改變仿人智能PID 控制的參數,該結果表明仿人智能PID控制具有較好的內在穩定性。 圖11 遷安波激勵下不同控制策略結構各層響應峰值Fig.11 The peak structural response of each floor with different control strategies under Qian′an wave excitation 文中提出了一種仿人智能PID 控制算法,其本質是基于層間相對位移大小和變化趨勢來控制MR 阻尼器的工作電壓,能夠有效減小結構的動力響應。通過研究分析得到如下結論: (1)MR阻尼器的力學性能試驗表明,Spencer模型可以比較準確地描述MR阻尼器的力學特性。 (2)數值結果表明,PID控制和仿人智能PID控制均具備對系統動態修正的特點,兩者較2種被動控制模式均具有較好的控制效果,但仿人智能PID 控制性能更高一籌,其對上層的相對位移、層間位移和絕對加速度控制效果均比兩種被動控制和PID控制好,說明基于MR阻尼器的仿人智能PID控制在建筑結構振動控制應用中的可行性和有效性。 (3)對比仿人智能PID控制與理想的主動控制方法,仿人智能PID控制在降低頂層相對位移峰值方面的性能比線性主動控制略好,并且仿人智能PID控制的最大層間位移要比主動控制的控制效果好,另一方面二者對結構控制的平均效果相差較小,說明仿人智能PID控制可以達到甚至超過理想主動控制的性能。 值得注意的是,文中通過數值方法對所提控制算法的可行性和有效性進行了驗證,但尚未進行振動臺試驗,有關該控制方法的進一步研究將在后續工作中展開。4 數值模擬與分析

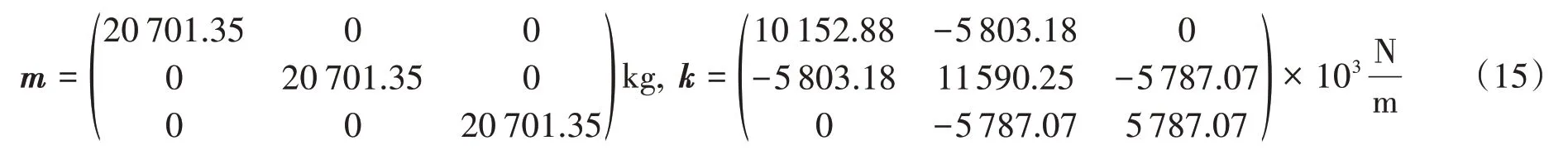




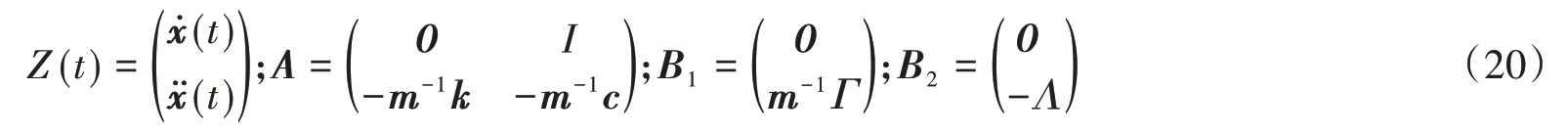



5 結論

