基于卷積神經網絡的近壁流動高分辨率平均速度場預測方法

王少飛，潘翀2,,，齊中陽

1.北京航空航天大學寧波創新研究院 先進飛行器與空天動力創新研究中心，寧波 315100

2.北京航空航天大學 流體力學教育部重點實驗室，北京 100191

0 引 言

在流體邊界層中，由于流體黏性在固體壁面產生摩擦阻力，因此摩擦阻力的精確測量對于評估載運工具的力學特性具有重要意義。常規摩阻測量方法可以分為直接法和間接法。直接法使用摩阻天平進行測量，存在諸如安裝誤差、流動干擾以及加工成本高等缺點。間接法通過獲取壁面附近的某些物理量間接測量摩阻，如采用粒子圖像測速（Particle Image Velocimetry，PIV）或粒子追蹤測速（Particle Tracking Velocimetry，PTV）對邊界層近壁區流動進行精細化測量，進而通過計算黏性底層的速度梯度來估算摩阻，其精度主要依賴于黏性底層中平均速度梯度的精度。

PIV 通過追蹤跨幀示蹤粒子圖像對（下文簡稱粒子圖像對）中一定查詢窗口區域內粒子群的位移來得到查詢窗口區域的平均速度，常用查詢窗口尺寸為32 像素×32 像素，此方法的空間分辨率受限，不適用于速度梯度大（如黏性底層）的場景。 為了提高PIV 在邊界層測量中的空間分辨率，研究人員提出了多種改進方案，如Nguyen 等采用長方形窗口、Willert和申俊琦等采用單行窗口均可得到法向空間分辨率較高的瞬時邊界層速度場，進而估算瞬時摩阻。Shen將micro-PIV 中的平均互相關法擴展為單像素系綜平均互相關法（Single Pixel Ensemble Correlation，SPEC），將速度場的空間分辨率提高至單像素精度。但該方法對粒子圖像對樣本總數要求高，粒子圖像對的數量在O（10～10）幀才能獲得較好的結果。PTV 則通過追蹤單個粒子的位移得到高空間分辨率速度場，但需要進行粒子識別和跨幀匹配，且匹配算法自由度大，匹配精度受粒子濃度和跨幀位移的影響較大。

近年來，眾多研究人員受深度學習在計算機視覺領域內所取得的重大突破的啟發，將神經網絡應用于邊界層流動特性預測中，開辟了神經網絡邊界層預測的新方向。如，Cai 等提出了PIV–NetS網絡架構，其具有典型的光流網絡特點，將粒子圖像對灰度圖作為神經網絡輸入、已知的高分辨率速度場作為真值訓練光流神經網絡。在訓練完成后，神經網絡能夠基于實驗獲得的粒子圖像對輸出高分辨率速度場。Lagemann 等提出了RAFT–PIV 架構，先將粒子圖像對通過卷積層進行特征提取，然后對特征圖進行互相關操作，將相關信息輸入到卷積循環單元中預測高分辨率速度場。以上研究的一個實際限制在于均需預知高分辨率速度場信息作為神經網絡輸出端的真值，因此大部分研究均基于數值計算得到的速度場構造虛擬粒子圖像對，形成神經網絡的訓練集。在實際實驗中，粒子濃度、粒徑、形狀、分布和光照條件等圖像信息千差萬別，通過虛擬粒子圖像對訓練出來的神經網絡能否適用于實驗測量獲得的示蹤粒子圖像對是一個需要考慮的制約性條件。因此，本文并未采用此類技術路線，而是提出了一種新的基于PTV 思想的耦合卷積神經網絡（Convolution Neural Network，CNN）高分辨率平均速度場預測方法，即CNN–PTV。該方法先將實驗獲得的粒子圖像對樣本集作為CNN 的輸入和輸出，訓練獲得僅能預測該樣本集所包含的平均流動的CNN，再進一步使用該CNN 預測單個粒子的跨幀位移。該方法解決了訓練神經網絡真值難以獲取的問題，也規避了傳統PTV 需要進行多粒子跨幀匹配的難點，可獲得基于粒子圖像對樣本集的高分辨率平均速度場。

1 CNN-PTV 神經網絡架構

圖1為基于CNN–PTV 的邊界層平均速度場預測思想示意圖，其分為CNN 訓練和平均速度場預測兩個階段。在訓練階段，將實驗測量獲得的一組跨幀粒子圖像對樣本集中的第一幀和第二幀分別作為CNN 的輸入和輸出真值，使用均方誤差函數作為訓練損失，使神經網絡輸出的粒子灰度分布信息逼近第二幀真值的灰度分布信息。遍歷整個圖像對樣本集，使得CNN 收斂。訓練完成后，CNN 隱含了訓練樣本集在整個像素空間中的平均光學流動信息。在流場預測階段，將人工合成的只含單個粒子的圖像輸入到CNN 中，輸出圖像即為該粒子經過當地平均流動的對流在第二幀上的成像。通過高斯擬合確定單個粒子的中心位置（達到亞像素精度），即可對單個粒子進行跨幀追蹤。將單個粒子遍歷整個像素空間，即可獲得空間分辨率達到像素精度的二維平均速度場。

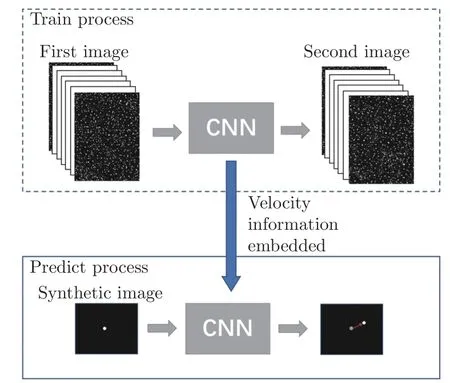
圖1 基于CNN-PTV 的平均速度場預測流程Fig.1 The ensemble velocity field predicted process by CNN-PTV

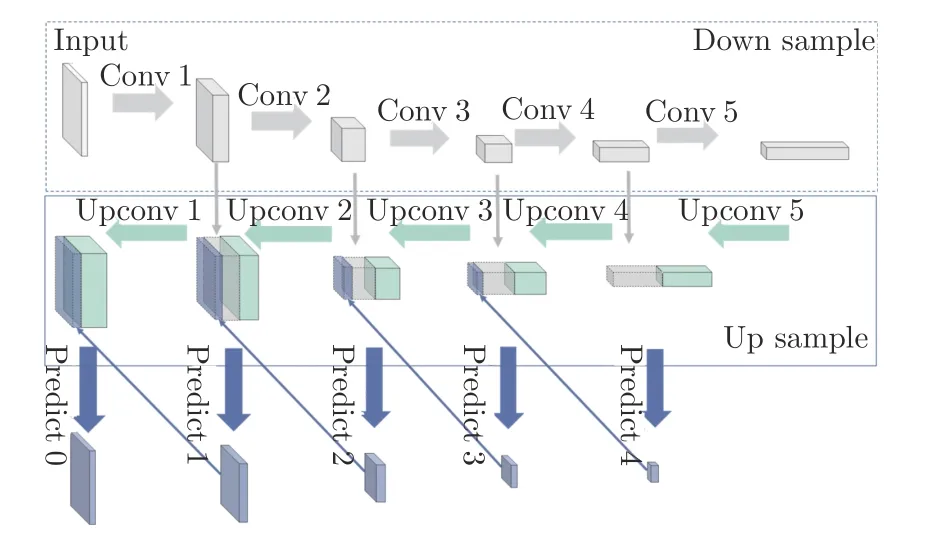
圖2 CNN 結構示意圖Fig.2 Schematic view of complete network architecture

表1 所測試CNN 的不同配置參數及損失Table 1 The parameters set in various tested cases

2 粒子圖像對訓練樣本集

本文采用人工合成的虛擬粒子圖像對測試CNN–PTV 算法預測近壁平均流動的能力，將預測的平均速度場與真實流場進行對比，并分析其誤差特性。采用S.I.G 框架生成虛擬粒子圖像對，依據已知速度場生成在像素空間內具有高斯分布特性的灰度粒子圖像對。用于生成虛擬粒子圖像對的參數設置如表2所示，共生成2 000 對粒子圖像對。圖像尺寸為68 像素×128 像素，接近真實近壁測量實驗中近壁黏性底層的圖像分辨率，便于后續直接應用。每一對圖像上粒子團位移均服從邊界層近壁平均流動的壁面率，即壁面傾斜角度為5°，兩幀圖像上平行于壁面方向的粒子最大位移為12 像素，垂直于壁面方向的粒子移動速度為0。 本文暫不考慮時序脈動量，速度場均為平均速度場。平均粒子直徑為4 像素，灰度分布符合二維高斯分布。粒子濃度首先設置為32 像素×32 像素的窗口中存在約12.8 個粒子，單個像素位置上的粒子數，即單像素粒子濃度（particle per pixel，p.p.p.）為0.012 5。圖3為人工合成的粒子圖像對及速度分布示意。為簡化討論，后文中速度的單位均為像素/單位時間。

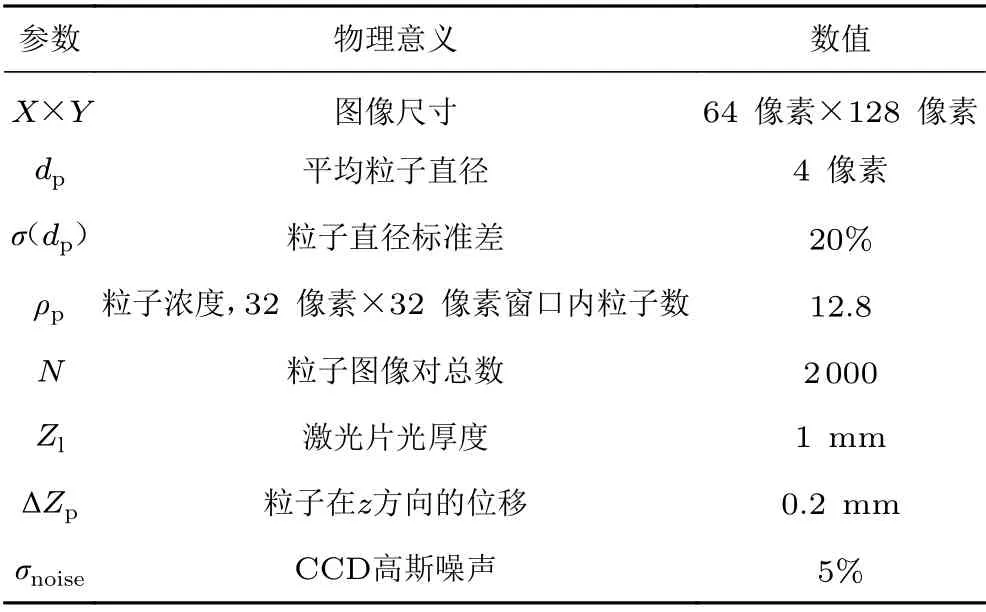
表2 人工合成虛擬粒子圖像對的參數設置Table 2 List of particle image parameters

圖3 人工合成虛擬粒子圖像對及速度示意Fig.3 One snapshot of synthetic particle image in a steady near-wall flow field

3 平均流動運動預測

圖4為不同神經網絡配置和訓練策略下CNN的損失曲線，其中實線為驗證集損失，虛線為訓練集損失。在不增加激活層的前提下，神經網絡非線性擬合能力弱，損失一直保持較高值，輸出粒子圖像對上的大部分粒子邊緣虛化，無法準確預測粒子移動。增加Relu 激活層并增加卷積核大小和深度后，CNN 中可訓練參數增多，對訓練數據的擬合能力增強，損失持續減小。在Case 8～10 測試中采用了多層加權損失作為損失函數，可以看到收斂后的損失進一步減少。此外，經過測試，改變學習率以及訓練批大小對減小損失沒有明顯效果。

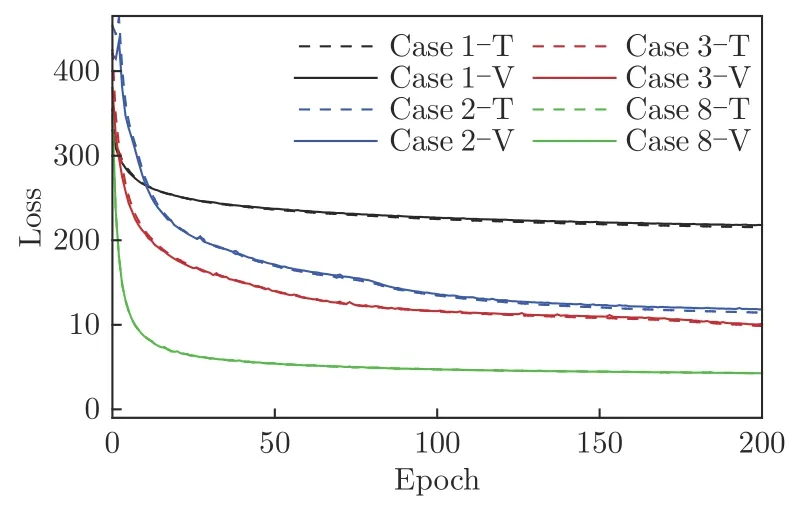
圖4 不同配置神經網絡訓練過程中的損失曲線Fig.4 Loss curves in various cases

CNN 對第一幀輸入粒子圖訓練后的輸出結果及其與真實第二幀粒子圖進行的對比如圖5所示。其中，紅色為真實粒子，綠色為預測粒子，當二者重合時則呈現為黃色。當訓練損失減小到一定程度但未完全收斂時（Epoch=100，圖5（a）），如圖5（b）所示，神經網絡的輸出圖像上下側已出現清晰的粒子光斑，預測粒子位置已與該區域內真實粒子接近重合；僅在圖像中部存在一些較為虛化的粒子，在流向上呈現拖尾現象，預測的虛化粒子也基本位于真實粒子附近，此時神經網絡不能完全確定此區域內粒子的移動位置。隨著訓練的持續進行，訓練集和樣本集上損失持續減小，完全收斂后（Epoch=200，圖5（c）），如圖5（d）所示，CNN 預測得到的第二幀圖像中虛化拖尾粒子減少，預測得到的粒子在大部分位置上與真實粒子重合。

圖5 神經網絡預測粒子圖及與真實粒子圖對比Fig.5 Comparation of predicted particles with real ones

訓練結束后，神經網絡中已經隱含了平均速度場信息。將只包含單個粒子的圖像輸入到神經網絡中，此時神經網絡將預測出此粒子在圖像上的位移。因只包含單個粒子，無需進行粒子匹配，只需通過高斯擬合即可確定粒子中心位置，進而得到當地位移信息。通過將此虛擬粒子遍歷圖像所有位置即可獲得高分辨率平均速度場。圖6為不同神經網絡預測得到的高分辨率速度云圖和真實速度云圖。可以看到，Case 8 得到的速度場已經十分接近真實值，而Case 6 和Case 7 得到的速度場在圖像中部仍存在一定的偏差，即在x 方向上中部區域存在階梯狀誤差，在y 方向上速度分量數值較小，預測得到的速度場明顯不光滑。

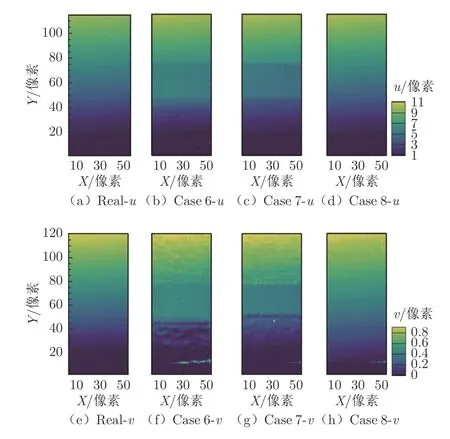
圖6 神經網絡預測高分辨率速度場云圖Fig.6 Contour plot of high-resolution predicted velocity field in Case 6-8 compared with real ones

圖7為Case 8 的預測速度場絕對誤差以及與相同樣本集下單像素系綜互相關（SPEC）所得結果的對比。e和e分別為水平和垂直速度分量誤差，e為絕對速度誤差。f（|e|）和F（|e|）分別為絕對速度誤差概率密度函數及累計分布函數。 SPEC 算法將互相關窗口縮小為單個像素，通過增加樣本數量可以得到高精度、高分辨率的邊界層速度場，但需要的粒子圖像對數量較多。對比二者速度分量誤差分布圖（圖7（a）和（d））可以發現，采用2 000 對粒子圖像對時，SPEC 算法兩個方向上速度分量誤差均控制在0.1 像素內；CNN–PTV 方法得到的誤差分布圖則將誤差控制在了更小的范圍內，水平方向絕對誤差略高于垂直方向，但基本均小于0.05 像素。兩個方向上速度分量誤差的差異可能是由于CNN 在預測粒子圖像對時存在偏差，在速度分量高的方向上偏差更為明顯。這一點可以從未收斂的虛化粒子圖像對上體現，如果第二幀粒子圖像對上的粒子在流向上出現拖尾，則難以精準確定其中心的流向位置。從速度分量的概率密度分布（圖7（c）和（f））可以看出，CNN–PTV 在x 方向上存在約0.02 像素的系統偏離。將絕對速度值累計分布的95%置信區間位置作為測速誤差，對比CNN–PTV 與SPEC 的測速誤差可以看出： CNN –PTV 的測速誤差約為0.052 像素，SPEC 的測速誤差則為0.095 像素（圖7（b）和（e））。因此，此工況下CNN–PTV 對平均速度場的預測精度略高于SPEC。

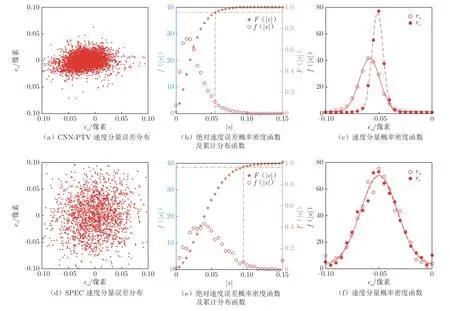
圖7 速度場預測絕對誤差Fig.7 The absolute error of predicted velocity in image coordinate system

圖8為近壁處壁面法向和水平方向平均速度曲線及其絕對誤差分布，其中黑色為真值，紅色為Case 8 中CNN–PTV 預測結果，綠色為SPEC 預測結果。橫坐標y為垂直于壁面方向的像素距離，u和v分別為平行和垂直于壁面的速度分量，e和e分別為其絕對誤差。從圖中可以看出，CNN–PTV 預測得到的邊界層平均速度曲線分布與真值貼合，偏離點比SPEC 更少。從垂直和平行壁面速度分量的絕對誤差分布上可以看出，CNN–PTV 方法的絕對誤差比SPEC 略小，大部分區域不超過0.03 像素。

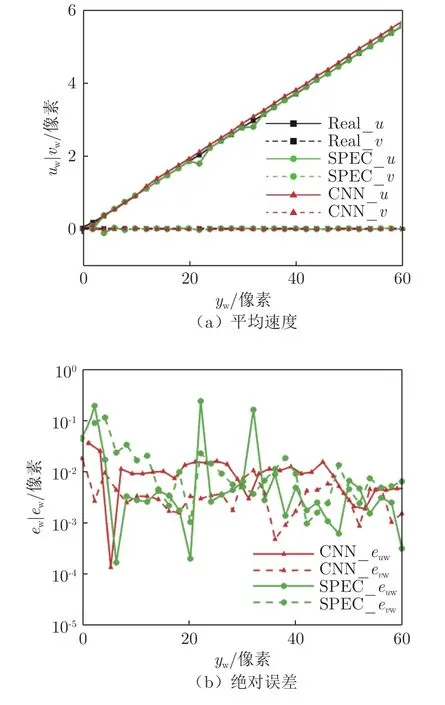
圖8 壁面法向和水平方向平均速度曲線及其絕對誤差分布Fig.8 Mean velocity profile in wall coordinate system and the absolute errors in two dimensions

4 粒子濃度和訓練集樣本數對預測精度的影響

Shen 等的研究已經表明，在使用SPEC 獲得平均速度場信息時，其預測精度受粒子圖像對樣本數以及粒子濃度影響較為明顯。神經網絡算法作為典型的監督型學習方法，其擬合效果也同樣受限于樣本本身包含的信息。因此，有必要考察粒子濃度和樣本數對本文發展的CNN–PTV 方法預測精度的影響。

圖9為粒子濃度對 CNN–PTV 方法的訓練損失和速度場預測誤差的影響。粒子濃度度量標準采用p.p.p.，絕對速度誤差（|e|）采用第3 節中定義的誤差累積分布95%置信區間位置。第3 節采用的粒子濃度為32 像素×32 像素內存在約12.8 個粒子，對應的p.p.p.濃度為0.012 5。如圖9所示，當粒子濃度持續降低時，驗證集損失持續降低，且未出現過擬合現象。粒子濃度對CNN–PTV 方法的平均速度場預測誤差的影響并不顯著，約為0.05～0.08 像素，說明該方法對粒子濃度不敏感。當粒子濃度降低至32 像素×32 像素內只存在約3.2 個粒子（p.p.p.=0.003）時，仍能取得較好的預測精度。與之相比， SPEC 算法對粒子濃度十分敏感，平均速度場預測誤差隨粒子濃度減小而持續增大，當p.p.p.低于0.006 時，只采用2 000 對粒子圖像對時無法得到可信的平均速度場。CNN–PTV 方法相對于SPEC 算法的優勢之一可做如下解釋：對于CNN–PTV 方法而言，在訓練過程中，只要求CNN 的輸出與第二幀粒子圖灰度分布一致即可。當粒子濃度降低時，計算得到的灰度均方誤差也會相應減小，但訓練完成后其仍能準確預測出不同位置處灰度的整體變動，即不論粒子濃度大小，CNN 總能預測出訓練樣本上粒子的整體平均位移。

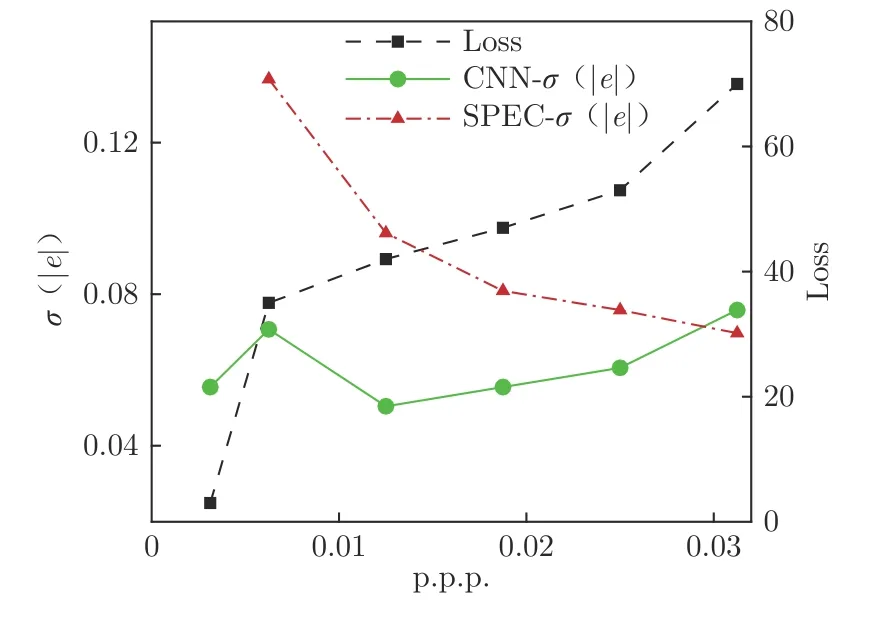
圖9 粒子濃度對訓練損失及速度場預測誤差的影響Fig.9 Dependence of loss and velocity field prediction error on particle density

圖10 為訓練樣本數對CNN–PTV 方法的訓練損失和速度場預測誤差的影響。32 像素×32 像素內的平均粒子數為12.8（p.p.p.=0.012 5），CNN 結構為表1中的Case 8。圖10 還顯示了同樣本集下SPEC的結果以便對比，如圖所示，訓練樣本數減小時，CNN–PTV 方法的訓練損失增大，且速度場預測誤差相應提高。對于所有的測試樣本數量，SPEC 的速度場預測誤差均高于CNN–PTV 方法，且當樣本數低于1 000 時SPEC 算法失效，而CNN–PTV 在樣本數為200 時的誤差仍小于0.1 像素。

術前，兩組焦慮、強迫、抑郁、恐怖、人際關系、偏執評分比較，差異均無統計學意義(P>0.05)。手術當日及術后2 d，兩組焦慮抑郁評分比較，差異有統計學意義(P<0.05)，其余評分比較，差異無統計學意義(P>0.05)。術前、手術當日及術后2 d強迫因子得分于均高于陽性分值(2分)，術前偏執因子得分高于陽性分值。見表1。

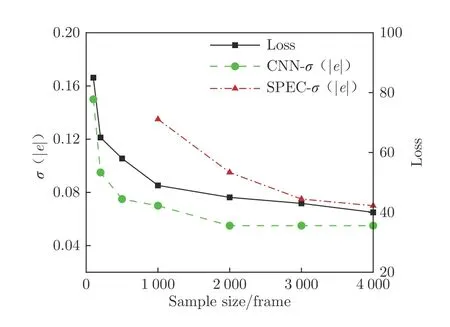
圖10 訓練樣本數對訓練損失及速度場預測誤差的影響Fig.10 Dependence of loss and velocity field prediction error on sample size

5 結 論

本文設計了一種CNN–PTV 架構，主要用于預測邊界層近壁區（黏性底層以內）的平均速度場。其包含了兩個步驟：在訓練階段，采用真實粒子圖像對構成的訓練樣本集對CNN 進行訓練，使其具備預測單個粒子的平均跨幀位移的能力；在預測階段，使用CNN 預測任意像素位置上單粒子的移動，最終得到像素級的平均速度場。此方法無需預知速度場信息，訓練獲得的CNN 僅能預測樣本集所涵蓋的平均流動，不具有泛化能力。但是，正是這種特應性使得CNN 的訓練不需要傳統光流CNN 所依賴的大樣本訓練集，因此其訓練過程簡單、收斂容易。

通過優化CNN 的網絡構型和訓練策略，CNN 可以精準預測粒子的灰度分布，進而得到高精度的平均速度場分布。仿真測試表明，本文提出的CNN–PTV 方法對平均速度場的預測精度略高于傳統的SPEC 算法，且對粒子濃度不敏感，在訓練樣本較少的條件下仍能取得對邊界層近壁平均速度場較為可信的預測。

本研究中的神經網絡應用還僅限于黏性底層內人工合成的虛擬粒子，在后續研究中將擴展到真實實驗獲取的黏性底層粒子圖像對，對諸如環境噪聲、流場脈動等因素引起的粒子圖像對不穩定導致的誤差進行分析。

本文得到國家自然科學基金 （項目號：91952302，12002022）的資助。