巧避材料暗示 促進深度學(xué)習(xí)
——《三角形的面積》教學(xué)實踐與思考

文 許燕萍 俞 軍（特級教師）

【課前思考】

隨著課程改革的不斷深入，教師的教學(xué)理念也在不斷更新。《三角形的面積》一課教學(xué)，廣大教師已將重點從三角形面積公式的掌握和熟練運用轉(zhuǎn)變?yōu)槿切蚊娣e公式的理解上，也看到很多案例中安排了大量的實踐操作活動去探究面積公式的由來。

但如何在這些探究活動中充分暴露學(xué)生的原生態(tài)思維，拓寬他們的思維廣度，最大限度地挖掘解決問題的多種策略，從而讓學(xué)生深刻體驗到知識產(chǎn)生的過程，讓學(xué)生的數(shù)學(xué)學(xué)習(xí)真正發(fā)生，顯然還有待深入研究。因此，筆者將從探究材料入手，不再提供給學(xué)生可操作的兩個完全一樣的三角形（分三類），而是讓學(xué)生先想一想，然后再在《學(xué)習(xí)單》上畫一畫思考過程，并借助表達想法、動手操作、課件演示來更直觀、更多元地展示圖形的轉(zhuǎn)化過程，從而拓展學(xué)生的思維空間，發(fā)展學(xué)生的空間想象力。

【教學(xué)目標】

1．經(jīng)歷三角形面積計算公式的推導(dǎo)過程，理解三角形面積計算公式的由來，并正確運用三角形面積計算公式進行計算。

2．進一步發(fā)展學(xué)生的空間想象力，體會轉(zhuǎn)化的數(shù)學(xué)思想。

3．在自主探究中獲得積極的情感體驗，進一步培養(yǎng)學(xué)習(xí)數(shù)學(xué)的興趣。

【教學(xué)過程】

一、激活已有經(jīng)驗，適時導(dǎo)入課題

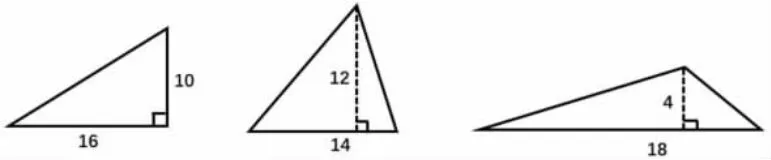
上課伊始，教師借助多媒體直接出示上面三類三角形（先不給數(shù)據(jù)），問學(xué)生：你看到了什么？（生：直角三角形、銳角三角形、鈍角三角形）

（然后課件出示數(shù)據(jù)）你又看到了什么？（生：三角形的底和高分別是多少）好的，今天我們就一起來研究三角形的面積。（板書課題）

【思考：上課伊始，教師直接出示三種不同類型的三角形，在沒有數(shù)據(jù)的干擾下，促使學(xué)生回憶起三角形的分類，有效激活已有經(jīng)驗，為本節(jié)課將要從這三類三角形展開研究做鋪墊。另外，開門見山引入課題，有效激發(fā)了學(xué)生的探究欲望，使他們迅速將思維轉(zhuǎn)移到本節(jié)課的研究內(nèi)容上。】

二、直面挑戰(zhàn)性任務(wù)，暴露學(xué)生思維

師：同學(xué)們，如果讓你任選一類三角形來研究，你會選哪個？（生:直角三角形）現(xiàn)在我們要研究直角三角形的面積，你會怎么想？先把你的想法在這個直角三角形上畫一畫，然后再算一算，請完成《學(xué)習(xí)單》的第一題。（學(xué)生獨立探究，教師關(guān)注學(xué)生探究的情況，及時了解學(xué)生的探究過程及計算背后的思考過程）

【思考：以上教學(xué)環(huán)節(jié)，看似無意，實則別有用心。在以往的教學(xué)過程中，教師通常會為學(xué)生準備好類似這樣的學(xué)具：提供兩個完全一樣的三角形（分三類）。從前期的磨課中發(fā)現(xiàn)，這樣的安排無意中局限了學(xué)生的思維，使其在想到拼組的方法后很難再去思考別的方法。因此，我們決定不再為學(xué)生提供兩個完全一樣的三角形，而是讓學(xué)生先想一想，再把思考過程在《學(xué)習(xí)單》上的直角三角形中畫出來，由于學(xué)生已有的活動經(jīng)驗和思考的角度不同，解決問題的策略也不盡相同，故此環(huán)節(jié)為學(xué)生有效創(chuàng)設(shè)了探究的時空，能充分暴露學(xué)生的原生態(tài)思維。】

（教師巡視并找到學(xué)生的以下三種轉(zhuǎn)化方法，并逐個投影反饋）

師：同學(xué)們，請看大屏幕，有同學(xué)是這么做的（指著圖1），誰能看明白？

師：（追問）隨便兩個直角三角形都能拼嗎？（兩個完全一樣的直角三角形才可以拼）

師：老師這里就有兩個完全一樣的直角三角形，按照你的意思把它拼成長方形（緊接著教師用實物演示，并貼到黑板上）。剛才我們這樣拼是拼成了（生：長方形），如果這樣拼就拼成了（生：平行四邊形）。

師：（追問）但這兩種拼法都可以用哪個算式來計算？（16×10÷2）

師：下面我們來看第二種想法（指著圖2），先請主人來說說他是怎么想的。（生：我是沿高的一半剪開，然后把它拼成一個長方形）

師：（追問）高的一半怎么找呢？誰有好辦法！（生：對折）好，那老師把它沿著高對折，（教師沿著高剪開）誰來幫老師拼一拼？（指名學(xué)生拼貼到黑板上）

師：現(xiàn)在我們把這個直角三角形轉(zhuǎn)化成了長方形，這個長方形的長是（16），寬是（10÷2），面積是16×（10÷2），這樣算出來的也就是（生：三角形的面積）。

師：同學(xué)們，這里還有第三種方法（指著圖3），猜猜他又是怎么想的？（他是沿著底的一半剪開，再把剪下來的左邊部分拼到上面，也拼成了一個長方形）

師：（追問）那底的一半怎么找啊？（生：也用對折）好，老師就照著你的意思對折并剪下來（教師演示），這次誰來幫我拼？（指名學(xué)生貼到黑板上）

師：（追問）這個長方形的面積怎么計算呢？（生：16÷2×10）這樣也就算出了（生：三角形的面積）。

小結(jié)：我們在研究直角三角形面積的時候，可以用兩個完全一樣的直角三角形拼成一個長方形或者平行四邊形，也可以將一個直角三角形割補成一個長方形，但是不管哪種方法，都是轉(zhuǎn)化成了我們已經(jīng)學(xué)過的圖形。

【思考：以上教學(xué)過程，教師利用印在《學(xué)習(xí)單》上的直角三角形這一探究材料，促使學(xué)生多角度地思考問題，激活了學(xué)生的多元思維，體會到了解決問題策略的多樣化，有效提高了學(xué)生解決問題的能力。同時，還適時滲透了轉(zhuǎn)化的數(shù)學(xué)思想。另外，在師生、生生間的交流、互動、碰撞中，學(xué)生的思維從模糊到清晰，從殘缺到完整，甚至從錯誤到正確，從而不斷完善了學(xué)生的思維。】

三、緊扣數(shù)學(xué)本質(zhì)，完善學(xué)生思維

師：同學(xué)們，我們繼續(xù)學(xué)習(xí)，請看大屏幕，現(xiàn)在還剩下哪兩類圖形？（生：銳角三角形和鈍角三角形）同桌商量一下，一人選一個，先畫一畫，再算一算。請拿出《學(xué)習(xí)單》來試一試，做完后可以同桌交流一下各自的想法。

教師在巡視中有意識地選擇銳角三角形的三種典型計算方法，并請學(xué)生板書到黑板上，具體如下：

方法①：14×12÷2 方法②：14×（12÷2）

方法③：14÷2×12

師：好，同學(xué)們，請停下來！我們先來交流銳角三角形。你能看懂哪一種？

（學(xué)生交流到方法①時投影《學(xué)習(xí)單》的相應(yīng)思考過程，出示圖4）

師：（交流到方法②時）猜猜他是怎么剪的？還有不同的剪拼方法嗎？（教師根據(jù)學(xué)生匯報交流，適時呈現(xiàn)如圖5的兩種方法）

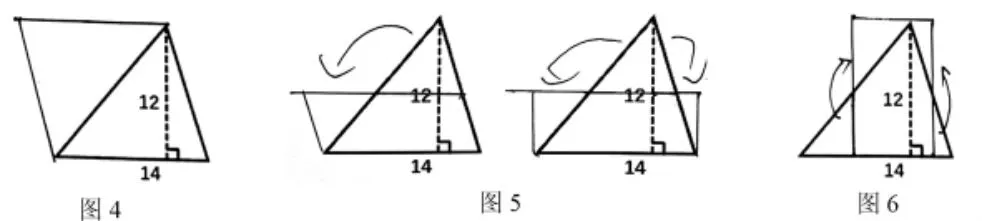
師：（繼續(xù)引導(dǎo)）不難發(fā)現(xiàn)這兩種方法都是沿著高的一半剪開，拼好的圖形和原來的三角形面積是（生：相等的），所以這個三角形的面積該怎么算？（生：12÷2×14）。

師：（交流到方法③時）他又是怎么想的呢？（生：沿底的一半剪開，但是不能對折，要兩邊分別對折剪開）（教師適時出示圖6）所以這個長方形的長是（生：14÷2），寬是（生：12），算式是（生：14÷2×12）。

師：還有同學(xué)選擇了鈍角三角形來研究，我們一起來交流（快速簡單交流）。

教師逐一呈現(xiàn)學(xué)生中典型的三種轉(zhuǎn)化方法（如圖7）：

師：同學(xué)們，你們真了不起！現(xiàn)在我們一起以動態(tài)的方式來回顧剛才的這幾種轉(zhuǎn)化過程。（教師課件動態(tài)演示轉(zhuǎn)化過程，如圖8）

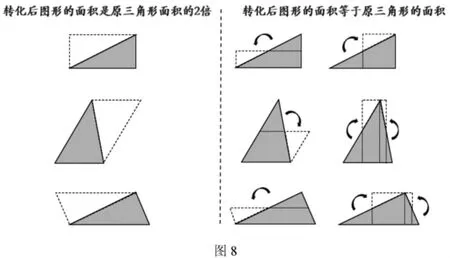
師：同學(xué)們，你們很厲害！想到了那么多的轉(zhuǎn)化方法，那么現(xiàn)在你們說一說三角形的面積可以怎么計算呢？（生：底×高÷2）這個呢？［生：底×（高÷2）］這個呢？（生：底÷2×高）其實，這三個公式的本質(zhì)是一樣的，一般情況下，三角形的面積公式就寫成：底×高÷2；其字母公式可表示為：S＝ah÷2。

【思考：在探究完直角三角形之后，引導(dǎo)學(xué)生自主探究其余兩類三角形的面積，學(xué)生在已有的直角三角形的活動經(jīng)驗上，能夠自主利用方法再次遷移，由特殊到一般，從而讓推理過程更嚴密。另外，通過大量的對三角形面積轉(zhuǎn)化過程的體驗與感悟，使學(xué)生對三角形面積公式的理解更為清晰和深刻，真正構(gòu)建起了三角形面積計算的模型，從而進一步有效促進了學(xué)生的深度學(xué)習(xí)。】

四、延長體驗過程，強化數(shù)學(xué)思維

師：（課件呈現(xiàn)基本練習(xí)）同學(xué)們，你們學(xué)得都很棒！現(xiàn)在老師要來考考你，請看屏幕（課件出現(xiàn)原始三角形，如圖9）。

師：如果讓你計算這個三角形的面積，你會想到哪些轉(zhuǎn)化方法？靜靜地想一想。（讓學(xué)生只在腦海中想，不作交流）

師：（課件出示圖10-①）這種轉(zhuǎn)化方法你想到了嗎？（課件出示圖10-②）這種轉(zhuǎn)化方法你又想到了嗎？（課件出示圖10-③）現(xiàn)在呢？（課件出示圖10-④）最后一個呢？

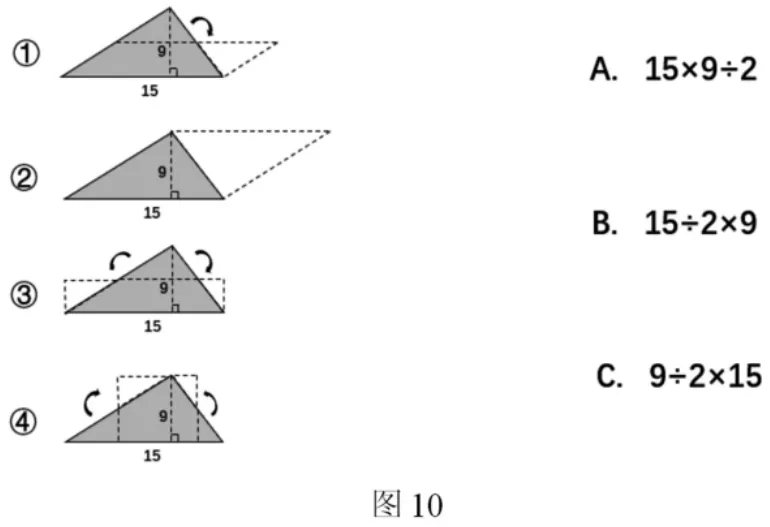
師：（再出示圖10中右邊三個算式）現(xiàn)在請你將轉(zhuǎn)化的方法和匹配的算式連一連。

師：同學(xué)們，請看大屏幕，和你連的一樣的請舉手。很棒！為你們點贊！

【思考：通過先想象，后找到轉(zhuǎn)化的方法，并和匹配的算式連一連，旨在引導(dǎo)學(xué)生進一步體驗、強化解決“三角形的面積是多少”這個問題的思維方式，而不是簡單、機械地套用公式，學(xué)生感悟到的是一種數(shù)學(xué)本質(zhì)，而非一個冷冰冰的公式。】

五、適時拓展延伸，提升學(xué)生思維

（課件呈現(xiàn)拓展練習(xí)）請你在下圖中畫一個三角形，使得它的面積與平行四邊形的面積相等。（每相鄰兩點之間的距離為1）

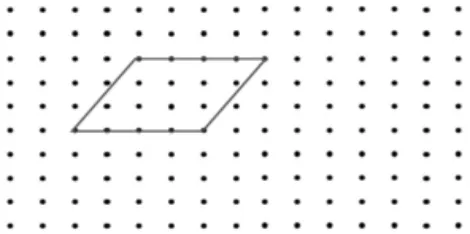
師：看來，這些數(shù)學(xué)問題都難不倒大家！下面我們繼續(xù)研究。請看大屏幕，自由地讀一讀要求。

師：同學(xué)們，題目讀完了，會嗎？請在《學(xué)習(xí)單》上試一試。

反饋預(yù)設(shè)：

1.展示底是4，高是6的作品（圖略）。我們先來看這位同學(xué)的作品，先請他說說是怎么想的？

生：當(dāng)三角形的面積和平行四邊形的面積相等，并且底也相等時，那么三角形的高必須是平行四邊形的高的2倍，這樣才能保證它們的面積相等。

2.展示高是3，底是8的作品（圖略）。我們再來看第二位同學(xué)的作品，誰能猜猜他是怎么想的？

生：當(dāng)三角形的面積和平行四邊形的面積相等，并且高也相等時，三角形的底必須是平行四邊形的底的2倍，這樣才能確保它們的面積相等。

3.展示底×高＝24的作品（圖略）。我們再來看這位同學(xué)的作品，請作者說說他又是怎么想的？

生：要保證三角形的面積與平行四邊形的面積相等，只要做到“底×高＝24”，然后再÷2就可以了。

【思考：表面上這是一個實踐操作題，但是考查的卻是學(xué)生的空間想象能力，萬變不離其宗的思維方式，以及逆向思考的能力。即無論怎樣想象及如何畫圖，只要三角形的面積算出來等于12就行；同時，還可以逆向思考，三角形的底乘高除以2等于12，那么底乘高只要等于24即可；還有當(dāng)三角形的底和平行四邊形的底相等時，高必須是兩倍關(guān)系才能保證它們的面積相等，從而有效提升了學(xué)生的數(shù)學(xué)思維和關(guān)鍵能力。】

六、滲透舉一反三，發(fā)展提問能力

師：好了，同學(xué)們，到現(xiàn)在為止我們已經(jīng)學(xué)會了如何求長方形、正方形、平行四邊形和三角形的面積，此時你又有什么新的問題要問老師或同學(xué)嗎？

生1：梯形的面積怎么求？

生2：圓的面積怎么求……

【思考：通過學(xué)生的提問，構(gòu)建起長方形、正方形、平行四邊形、三角形、梯形和圓的整體框架，為后續(xù)學(xué)習(xí)梯形的面積、圓的面積做好鋪墊，同時也培養(yǎng)了學(xué)生的知識遷移能力。】

【課后思考】

1.精設(shè)探究材料，開放學(xué)生思維。

材料引起學(xué)習(xí)、材料引起活動，學(xué)習(xí)材料是我們解決問題和形成數(shù)學(xué)思維的基本保證。本課最大的特點是探究性學(xué)習(xí)材料的精心設(shè)計，沒有像大多數(shù)教師一樣給學(xué)生提供兩個完全相同的三角形（分三類提供），而是呈現(xiàn)給學(xué)生三個不同類型的三角形，引導(dǎo)學(xué)生通過想一想、畫一畫、算一算的數(shù)學(xué)活動，完成三角形面積公式的推導(dǎo)。在此活動中，學(xué)生的思維不受學(xué)習(xí)材料的影響，可以想到用兩個完全一樣的三角形進行拼組，也可以想到把一個三角形進行剪拼，避免了不敢剪、剪壞了沒有材料可用的尷尬場面。另外，“先想再畫”對學(xué)生的空間想象能力提出了更高的要求，但它能充分暴露學(xué)生的原始思維，有效提升學(xué)生的想象能力和思維能力。

2.遵循學(xué)習(xí)軌跡，實現(xiàn)順學(xué)而導(dǎo)。

從學(xué)生思考的角度出發(fā),更容易發(fā)現(xiàn)問題,而問題本身往往就是教學(xué)重難點。本堂課，教師始終遵循學(xué)生學(xué)習(xí)的思維軌跡，通過畫一畫的獨立思考，充分暴露學(xué)生的原始思維，在與他人交流的過程中，不斷積累思維的經(jīng)驗，逐步形成自己的合理的思維方法，真正實現(xiàn)了順學(xué)而導(dǎo)的教學(xué)理念。只有當(dāng)學(xué)生通過自己的思考，建立起自己的數(shù)學(xué)理解力時，他們才能真正學(xué)好數(shù)學(xué)。

3.設(shè)計多元體驗，促進深度建模。

本節(jié)課中，教師設(shè)計了兩個多向思維的環(huán)節(jié)，如探究直角三角形的面積時，由思維圖式得到計算的算式，而在銳角三角形和鈍角三角形時，卻由計算的算式回憶或猜想思考的過程。又如練習(xí)設(shè)計，第一個基本練習(xí)是根據(jù)推導(dǎo)方法選擇匹配的算式，在解決問題的過程中學(xué)生不再是簡單地套用公式，而是重現(xiàn)轉(zhuǎn)化過程，進一步理解三角形面積計算公式的數(shù)學(xué)內(nèi)涵。第二個拓展練習(xí)是根據(jù)三角形的面積公式反推底和高，通過推導(dǎo)、說理等過程，找到平行四邊形和三角形面積之間的內(nèi)在聯(lián)系。這樣的多元體驗，貴在引導(dǎo)學(xué)生從多層次多角度去思考問題，不僅能強化教學(xué)重點，突破教學(xué)難點，而且還可以激發(fā)學(xué)生的學(xué)習(xí)興趣，充分發(fā)揮出每一位學(xué)生的學(xué)習(xí)潛能，有效培養(yǎng)了每一位學(xué)生的創(chuàng)造力。

總之，科學(xué)的、客觀的、具有一定開放性的學(xué)習(xí)材料，能夠讓學(xué)生的數(shù)學(xué)思維充分拓展，解題策略豐富多元，從而讓學(xué)生的數(shù)學(xué)學(xué)習(xí)真正發(fā)生。