見微知著 明理啟教

鄒信武

1 高中數學新舊教材對比的必要性

《普通高中數學課程標準（2017年版）》（下文簡稱《標準》），提出了高中數學的學習要求：“四基”“四能”及“六核心素養”.2019年秋季學期，部分省份率先使用新教材，教材在《標準》下做了哪些改變？新教材對比舊教材有哪些優勢？又是如何體現核心素養下的數學教學？教師應如何利用好教材落實“素養”教學？……這些都是擺在高中教師面前的問題.因此，對比新舊教材，尋找和分析差異，探求編寫意圖，明確教學要求，是高中數學教師加深對教材理解、落實《標準》理念的必然要求.

本文選取了人教A版《普通高中數學教科書·數學》（2019年）的《等式性質與不等式性質》和人教A版《普通高中課程標準試驗教科書-數學》（2004年）《不等式與不等關系》為例進行比較分析（分別簡稱為“新教材”和“舊教材”）.這節內容是不等式的初始課，學生經歷用不等式描述現實中不等關系，推導與證明不等式性質的學習過程，并用不等式解決實際問題，恰好可以體現“用數學的眼光觀察世界，用數學的思維思考世界，用數學的語言表達世界”.因此，選擇這一節內容進行新舊教材的對比，對理解《標準》理念下教材編寫意圖和教師教學指導都是極其有幫助的.

2 高中數學新舊教材“不等式性質”編排對比

2.1教材位置和章節名稱的比較

新教材將舊教材必修5第三章《不等式》中3.1節《不等式與不等關系》調整至新教材第一冊第二章《一元二次函數、方程和不等式》2.1節，章節標題也發生了改變-《等式性質與不等式性質》.在新教材中，第一冊的第一章和第二章是高中數學學習的預備知識，在這節內容之前，學生學習了集合的有關概念、關系和運算，還學習了充分條件、必要條件，全稱量詞、存在量詞、全稱量詞命題和存在量詞命題的否定等簡易邏輯知識.

2.2 教學內容的比較

比較新舊教材，該節教學內容基本沒有變化，主要分為兩個部分：第一部分是通過生活和數學的例子，引導學生體會不等式的實際背景，感受不等式的重要性和廣泛應用，進而總結實數大小關系的基本事實;第二部分是類比得到等式性質的方法，歸納不等式的性質并進行簡單應用.

2.3教學課時的比較

舊教材中沒有明確將這一內容劃分課時，教學時往往根據教師對內容的理解分為兩課時，部分教師拓展教材內容，引入大量生活素材，引導學生用不等式描述客觀世界作為第一課時，實數以，6大小比較的事實及不等式性質作為第二課時;也有部分教師將實數以，6大小比較的事實及簡單應用放在第一課時，將不等式性質作為第二課時，都有其合理之處.而新教材中明確了課時分配，不等式實際問題抽象和“基本事實”作為一個課時，不等式性質單獨作為一課時，并且各自配備了練習.

2.4 教材的整體性

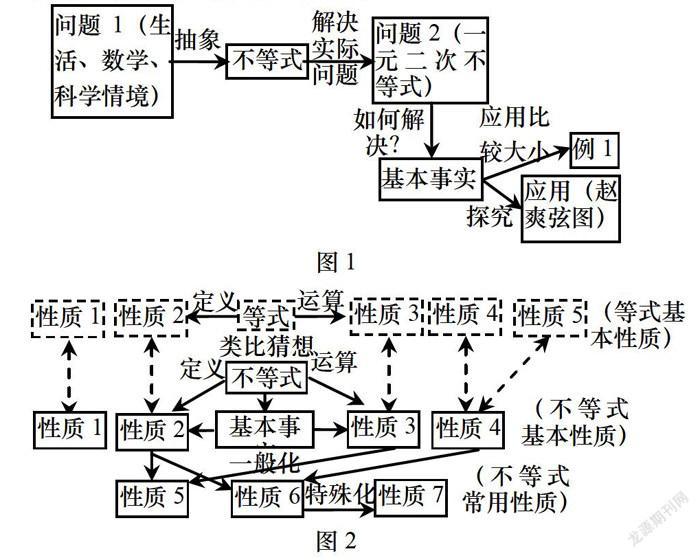
本輪課改另一個熱點就是“單元設計”.單元教學設計倡導按內容或思想方法重新整理教學內容，形成一個相對獨立的大單元.在新教材中，實數大小關系的基本事實是本章不等式知識的起始點，它是后面不等式知識的基礎.而等式與不等式的類比，是本章內容敘述的線索，其后面內容“解一元二次不等式”，也是基于對二次函數、二次方程、二次不等式的幾何直觀的理解上.在細節上，也處處體現著在這樣的安排，比如第一課時中問題2中的“二次不等式”，為2.3節“解二次不等式”埋下伏筆，引出探究案例趙爽弦圖，并證明重要不等式，為其后基本不等式提供邏輯基礎.這樣的安排，兼顧了知識的關聯性，保障了知識整體性，也更符合學生的思維規律，使學生從中領會數學思想，提升理性思維.

3“核心素養”視角下的新舊教材中的“不等式性質”

3.1數學抽象與直觀想象

數學抽象是指舍去事物的一切物理屬性，得到數學研究對象的思維過程[1].-般地，抽象經歷兩個過程：感性具體一理性具體一理性一般，它是符號化，形式化的過程.直觀想象主要包括幾何直觀與空間想象兩個方面.直觀想象是認識抽象對象的另一條途徑，它是符號化語言的直觀解釋.因此，教學中數學抽象對象與幾何直觀經常相輔相成，

在本節內容中，新教材更注重數學抽象形成過程，多角度、多維度地幫助學生經歷和體會抽象過程，感悟抽象對象的本質.在自然語言與符號語言的轉化過程中，新教材往往會給出它的幾何直觀，重視學生借助直觀理解數學內容，借助圖形描述和理解代數問題，比如“引入基本事實”過程中，舊教材僅僅限于自然語言抽象至符號語言，而新教材中在原有自然語言基礎上，加入圖象語言（數軸），更清晰地將抽象過程展露出來.又如：不等式性質3中，新教材增加了該性質在數軸上的幾何解釋，并給出提示：“從不同角度表述不等式的性質，可以加深理解，對其他不等式的性質，你能用文字語言表述嗎？”從符號語言再轉向自然語言或者幾何直觀，這是由理性一般轉向理性具體的過程，也是對抽象事物的更深層理解.

3.2 邏輯推理與數學運算

邏輯推理是指從一些事實和命題出發，依據規則推出其他命題的思維過程，在本課時中，邏輯推理是最重要的培養素養之一.邏輯推理主要包括合情推理和演繹推理.數學運算本質上是邏輯推理的一種形式.

邏輯思維素養的落實，首先要注意教學安排的邏輯性.新教材中，在《等式性質與不等式性質》第一課時中，教材內容的線索如圖1，在第二課時中，教材內容的線索如圖2.從圖中可以發現，新教材中，知識點間環環相扣，前后聯系，使學生對不等式的認識層層遞進，這樣的安排，既體現了數學知識的內在聯系，也符合學生認知規律，更能培養學生嚴謹思考問題的習慣.

邏輯推理素養的生成，需要學生經歷、感受推理的過程.對比發現，新教材更注重遵循學生思維規律，讓學生參與感受發現數學關系、數學規律的方法，通過邏輯推理證明結論的過程.如圖2，教材在等式性質與不等式性質采用了類比推理，讓學生從已有經驗中思考未經驗的內容，經歷分析、聯系、對比、猜想的過程;得到猜想之后，又從實數大小關系的基本事實出發，證明猜想，采用演繹推理的方式，從特殊到一般，再由一般到特殊，從性質再推導出新性質.在一節課上，學生就經歷了合情推理和演繹推理兩種推理過程，因此這塊內容是本節的重點和難點，是學生邏輯推理素養的養成關鍵性素材.

在本節內容中，數學運算在內容上是數學知識的紐帶，推進著數學知識的生成和學生的內化過程.如不等式性質的發現與證明過程，教材先是讓學生觀察，找到發現等式性質的基本方法——自身定義與運算，猜想出性質1～4，使用實數大小關系的基本事實進行證明（作差運算），再運用性質2、性質3和性質4推導性質5和性質6.再如例1的旁白注解“0是正數與負數的分界點，它為實數比較大小提供了標桿”，點出了問題的本質，明確了運算目的，讓學生探求運算思路，設計計算方法，這都體現了《標準》的要求.

3.3 數學模型

不等式作為描述現實世界不等關系的模型，兩套教材都設置了不等式的實際應用題，相比之下，新教材的例子更具趣味性，比如新教材中在習題2.1里面增加了第9題：“證明：圓的面積大于與它具有相同周長的正方形的面積，并據此說明，人們通常把自來水管的橫截面制成圓形，而不是正方形的原因”，第10題“糖水不等式問題”，給出了非常生活化的應用，用數學關系去描述和解釋生活現象，同時深化對不等式的理解，培養數學創新意識和實踐能力.

4 新舊教材《等式性質與不等式性質》對比的啟示

在《標準》下，新教材更注重學生的思維發展，教材處處體現著“學生主體”意識，知識作為載體，學生在經歷知識的產生、發展和應用，而要點不僅是知識本身，更重要的是在這一過程的體驗，以及在此過程中的程序性知識，這才是觸及學生核心素養的地方.基于本節內容，有如下幾點思考：

4.1 教學應遵循數學知識發生發展的邏輯

相比舊教材，新教材有更清晰、更完整的數學知識生成脈絡.教學中應注意把握數學知識的聯系與發展，使得數學知識的生成過程更自然.特別是第二課時，涵蓋數學知識多，涉及數學思想多，關系復雜，教學中應充分理解教材編排的意圖，把控全局，合理地調控“教學內容秩序”，展現給學生一個完整的知識系統.

4.2教學應留給學生更大的“思維空間”

《標準》的“四基”其中一條是“基本活動經驗”.在課堂上，除了生生、師生之間這類外在探討研究活動之外，更需要學生“獨立的思維活動”.本節內容包含大量的類比、推理和論證，需要學生進行大量深層次的思維活動.因而，遵循學生的思維規律，把握課堂節奏，在這些關鍵節點上留下足夠思考與交流的空間，是學生發展數學核心素養，從數學角度思考、分析和解決問題的保障.

4.3 挖掘教材隱性素材，促進學生思考

在教材中，許多表述會較為簡潔，部分知識“點而不破”，預留“空白”，教學中，教師應該挖掘教材中“空白處”，這是留給教師發揮的空間.如新教材中不等式性質1，教材沒有給出證明，我們可以提出問題：該如何證明性質17證明的依據是什么？這個證明看似簡單，但要有理有據，并不容易，需要使用實數大小的基本事實和實數的性質進行證明.又如：在不等式性質3推導性質5的過程，蘊含了特殊到一般的思想，性質6推導性質7，又蘊含了一般到特殊的思想，這些都是需要教師在教學中提煉和升華，使學生從中領悟數學思想，生成數學核心素養.

4.4 依托教育技術，將抽象直觀化

“符號化、形式化和公理化”是現代數學的重要特征.本節內容涉及較多符號化描述及運算，還有公理化的證明，具有高抽象、難理解的特點，教學中可以適當采用多種教育技術，加強其符號化的抽象表述的幾何直觀解釋，多角度呈現它的抽象過程，進而幫助學生加深對抽象對象的理解，

參考文獻

[1]史寧中，學科核心素養的培養與教學——以數學學科核心素養的培養為例[J].中小學管理，2017 （01），35-37

[2]朱立明，胡洪強，馬云鵬，數學核心素養的理解與生成路徑——以高中數學課程為例[J].數學教育學報，2018， 27（1）：42-46

[3]中華人民共和國教育部，普通高中數學課程標準（2017年版）[M].北京：人民教育出版社，2017