整體取勢、直觀明道、推理優(yōu)術，凸顯數(shù)學育人價值
——“平行線的性質”教學評析

周遠方，胡 華

（湖北省教育科學研究院；湖北省襄陽市教育科學研究院）

高原老師（以下統(tǒng)稱“執(zhí)教教師”）執(zhí)教的“平行線的性質”展示課例，是“第十二屆初中青年數(shù)學教師課例展示活動”的八個指定課題之一.該課例從E組脫穎而出，得到了本組學術委員和觀摩教師的一致好評，被評為本次展示活動的最優(yōu)展示課例.本文從課題背景、總體評價、亮點掃描和改進建議等四個方面對優(yōu)課展開評析，以期與大家分享、品賞和交流.

一、課題背景

《義務教育數(shù)學課程標準（2011年版）》（以下簡稱《標準》）和人教版《義務教育教科書·數(shù)學》七年級下冊（以下統(tǒng)稱“教材”）對“平行線的性質”的教學都提出了明確的要求和建議.

1.課題要求

“平行線的性質”是一節(jié)典型的幾何命題課，指定課題對其內容要求和教學提示如下.

（1）內容要求.

①掌握平行線的性質定理1：兩條平行直線被第三條直線所截，同位角相等.了解定理的證明.

②探索并證明平行線的性質定理2：兩條平行直線被第三條直線所截，內錯角相等.

③探索并證明平行線的性質定理3：兩條平行直線被第三條直線所截，同旁內角互補.

（2）教學提示.

要以單元整體教學思想為指導，引導學生在學習平行線的判定的基礎上，通過性質與判定的邏輯關系，猜想平行線的性質，通過演繹推理證明平行線的性質定理.教學中要盡量放手讓學生開展自主探究活動，加大教學的開放性，使學生在獲得性質定理的過程中經歷幾何命題發(fā)現(xiàn)和證明的過程，感悟歸納推理過程和演繹推理過程的傳遞性，培養(yǎng)推理能力.

2.《標準》要求

對“平行線的性質”的要求，主要從內容、教學和方法三個方面給出了相應的定位.

（1）內容定位.

“相交線與平行線”是初中數(shù)學“圖形與幾何”領域的基本內容，而“平行線的判定與性質”則是學生學會一些簡單的、基本的推理語言的起始內容，也是學生體會通過“推理”獲得數(shù)學結論的方法，培養(yǎng)言之有據(jù)的習慣和有條理地思考、表達的能力，從而完成從實驗幾何向論證幾何過渡的重要內容.

（2）教學定位.

圖形的性質的教學，需要引導學生理解歐幾里得平面幾何的基本思想，感悟幾何體系的一般觀念——通過定義確定論證的對象，通過公理確定論證的起點，通過證明確定論證的邏輯，通過命題確定論證的結果.因此，要強調研究幾何圖形的基本套路：實驗探究—直觀發(fā)現(xiàn)—推理論證.在用幾何直觀理解基本事實的基礎上，從基本事實出發(fā)推導圖形的幾何性質和定理，培養(yǎng)學生初步的推理能力，形成“擺事實、講道理”的科學精神.

（3）方法定位.

平行線性質定理的證明需要用反證法.因此，《標準》將其以“了解定理的證明”的要求定位，并作為“感悟反證法”的案例在附錄中給出了如下證明過程.

證明平行線性質定理：兩條平行直線被第三條直線所截，同位角相等.

例如圖1，設兩條平行線分別為AB和CD，被第三條直線EF所截，且直線AB被直線EF截于點O，我們要證明：如果AB∥CD，那么∠1=∠2.

圖1

證明：假設∠1≠∠2，過點O作直線A′B′，使∠EOB′=∠2.根據(jù)“同位角相等，兩直線平行”，可得A′B′∥CD.這樣，過點O就有兩條直線AB，A′B′都平行于CD，這與平行公理“經過直線外一點，有且只有一條直線與這條直線平行”矛盾.這說明假設∠1≠∠2不正確，從而得出∠1=∠2.

【說明】反證法是一種重要的數(shù)學證明方法，平行線性質定理的證明將是學生第一次接觸到反證法的證明，因此非常重要.在教學過程中，讓學生感知反證法的作用的同時，要力爭讓學生感悟反證法的邏輯和論證流程，感知矛盾律和排中律，形成初步的推理能力.

3.教材要求

學習本節(jié)課的內容時，要注意觀察實物、模型和圖形，通過觀察、測量、實驗、歸納、對比、類比等來尋找圖形中的位置關系和數(shù)量關系，從而發(fā)現(xiàn)圖形的性質；還要注意體會通過“推理”獲得數(shù)學結論的方法，培養(yǎng)言之有據(jù)的習慣和有條理地思考、表達的能力.同時，教材根據(jù)《標準》要求，結合教學實際，按照循序漸進的原則，將反證法的學習安排在九年級上學期“點和圓的位置關系”之中，在用反證法證明“不共線的三點確定一個圓”之后，給出了上述證明.

二、總體評價

平面幾何是理性思維的典范，邏輯推理是理性思維的完美體現(xiàn)，“借助圖形建立直觀，通過推理予以表達”是邏輯推理的精髓.圖形的性質與判定是幾何研究的核心問題，而圖形的性質主要研究圖形組成元素之間的相互關系.平行線的性質既是研究角的相等或互補關系的理論依據(jù)，又是研究幾何圖形位置關系和數(shù)量關系的知識基礎，也是學生系統(tǒng)學習圖形性質的開路先鋒.因此，在“平行線的性質”的教學中，如何使幾何直觀、邏輯推理綜合地發(fā)揮作用，就成為發(fā)展學生幾何直觀和推理能力素養(yǎng)的關鍵舉措.

本節(jié)課立足幾何命題教學“取勢、明道、優(yōu)術”的三部曲，創(chuàng)新了“平行線的性質”的教學方式，實現(xiàn)了“既見樹木，又見森林”的教學效果，充分展現(xiàn)了“用整體教學追求幾何直觀與邏輯推理融合發(fā)展”的教學特色（如圖2）.

圖2

1.整體取勢，確定研究方向

本節(jié)課采用單元設計和整體思想導學，承前啟后，確定研究方向，讓學生明確“為什么學”.通過整體設計體現(xiàn)一般觀念，利用“怎樣研究一類幾何圖形的性質”的大觀念引領，整體規(guī)劃研究思路，充分展現(xiàn)了實驗幾何到論證幾何的演繹之路，有效發(fā)展了學生的幾何直觀、抽象能力和推理能力素養(yǎng).

2.直觀明道，確定研究路徑

本節(jié)課采用類比學習和幾何直觀教學，以舊啟新，確定研究路徑，讓學生明確“學什么”.通過直觀類比構建學習路徑，利用直觀類比平行線判定的研究內容、過程、方法、順序等來研究平行線的性質，遵循幾何教學的基本套路（背景—定義—判定—性質—應用），構建了研究平行線的性質的單元學習路徑.

3.推理優(yōu)術，確定研究方法

本節(jié)課采用合情推理和演繹推理悟學，起承轉合，確定研究方法，讓學生明確“怎樣學”.通過邏輯推理演繹學習方法，利用觀察、實驗、猜想、驗證、推理等思維活動，重在讓學生經歷命題學習的完整過程（發(fā)現(xiàn)命題—提出命題—證明命題—運用命題），學會研究一個幾何對象的基本思路（直觀感知—操作確認—推理論證—度量計算），積累研究幾何圖形的基本活動經驗.

總之，本節(jié)課通過“在直觀中感知、在實驗中探索、在歸納中猜想、在動態(tài)中驗證、在演繹中推理、在交流中表征、在應用中解釋”等系列化的教學活動，師生共同合作，為我們展示了一節(jié)凸顯數(shù)學育人價值的優(yōu)秀課例.

三、亮點掃描

本節(jié)課無論是教學設計、教學課件和教學板書，還是教學視頻、教學反思和教學點評，都體現(xiàn)著執(zhí)教教師的獨具匠心，堪稱展示課的優(yōu)秀范本，其突出的“三精”亮點具體表現(xiàn)如下.

1.思想融合，教學設計精致

眼界決定格局，思想決定高度.本節(jié)課將單元整體設計思想、數(shù)學公理化思想、化歸與轉化思想和分類與整合思想融為一體，充分展現(xiàn)了“大概念，小單元；大問題，小延伸；大任務，小融合”的教學特色.通過充分挖掘教材，整合與“平行線的性質”有關的內容作為研究素材，在基于單元整體設計的同時，為后續(xù)的平移、三角形、四邊形等幾何圖形的學習提供了數(shù)量關系的理論支撐、思想方法的研究范式和幾何學習的基本套路.

本節(jié)課突出三條設計線索.以平行線的性質的探索、證明和應用為明線，以多種思想方法的融合為暗線，以多幅結構框圖的精心設計、多元教學素材的有效嵌入、多樣學習方式的綜合運用和系列化的研學活動為主線，呈現(xiàn)了一份豐富多彩、新穎別致和畫面感極強的教學設計.

2.過程融合，教學環(huán)節(jié)精當

只有重視過程，才能深刻領悟教學.本節(jié)課借鑒由一般到特殊研究相交線的習得經驗，結合將平行線判定的條件和結論反過來的逆向思維，基于“類比判定學性質”的認知方法，通過融合思維過程和認知過程來確定平行線的性質的研究過程，形成幾何研究的一般觀念.整個教學過程以“喚醒經驗，梳理思路—類比判定，問題驅動—開放探究，提出猜想—歸納推理，演繹論證—性質應用，問題解決”的順序展開，各個教學環(huán)節(jié)層層推進，環(huán)環(huán)相扣，邏輯結構清晰，教學流程合理，教學過程自然流暢，教學環(huán)節(jié)精當（如圖3）.

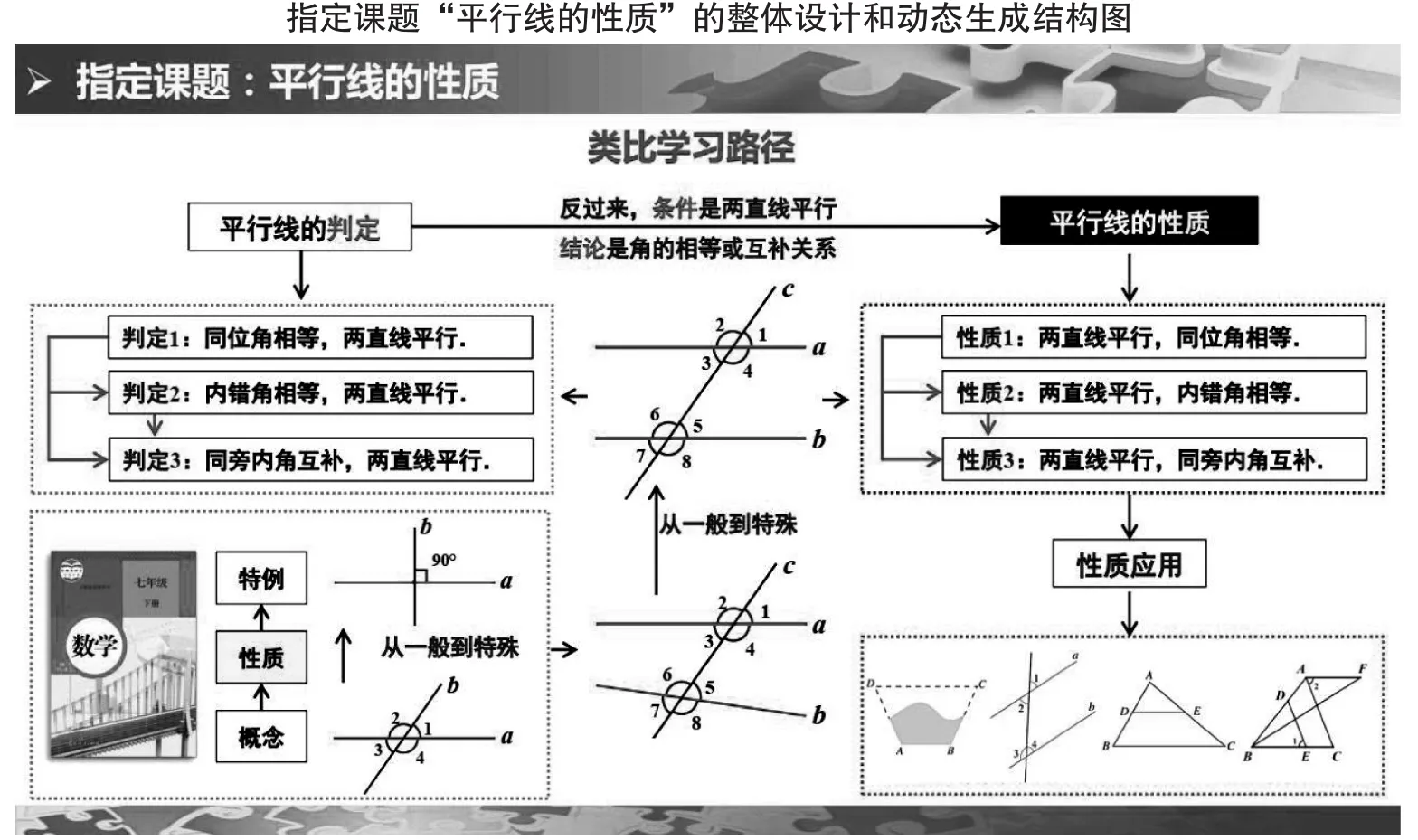
圖3

特別是面對學生的質疑過程：性質2和性質3都是通過嚴格推理證明得到，但為什么性質1卻只是通過實驗探索得到？教師及時引導學生明確：性質1將在以后的學習中利用反證法加以證明，現(xiàn)階段我們把性質1作為基本事實，運用公理化思想就可以利用基本事實來推理性質2和性質3.這一質疑互動的真實過程，真正體現(xiàn)了課堂教學的生成機智，不僅解答了學生的疑惑，而且詮釋了教材的編寫意圖——遵循幾何學習循序漸進和螺旋上升的原則，同時展現(xiàn)了教師具有較高的理解《標準》、理解教材和理解教學的專業(yè)功底和數(shù)學素養(yǎng).

3.手段融合，教學生成精彩

數(shù)學課堂教學因巧妙設計而精致，因動態(tài)生成而精彩，因理性思維而深刻.本節(jié)課從精選課堂教學手段和板書精心設計入手，依托整體設計和動態(tài)生成的結構圖（如圖3），提高了課堂教學的實效性；借助幾何畫板軟件動態(tài)驗證平行線的幾何特征，體現(xiàn)了信息技術的優(yōu)越性；通過作業(yè)分層設計的結構圖（如圖4），體現(xiàn)了“雙減”政策背景下的作業(yè)設計理念；等等.這一系列手段的合理運用，既有效體現(xiàn)了教材的編寫意圖，又將教學預設和課堂生成有機融為一體，也為數(shù)學探究學習提供了值得借鑒的教學案例.

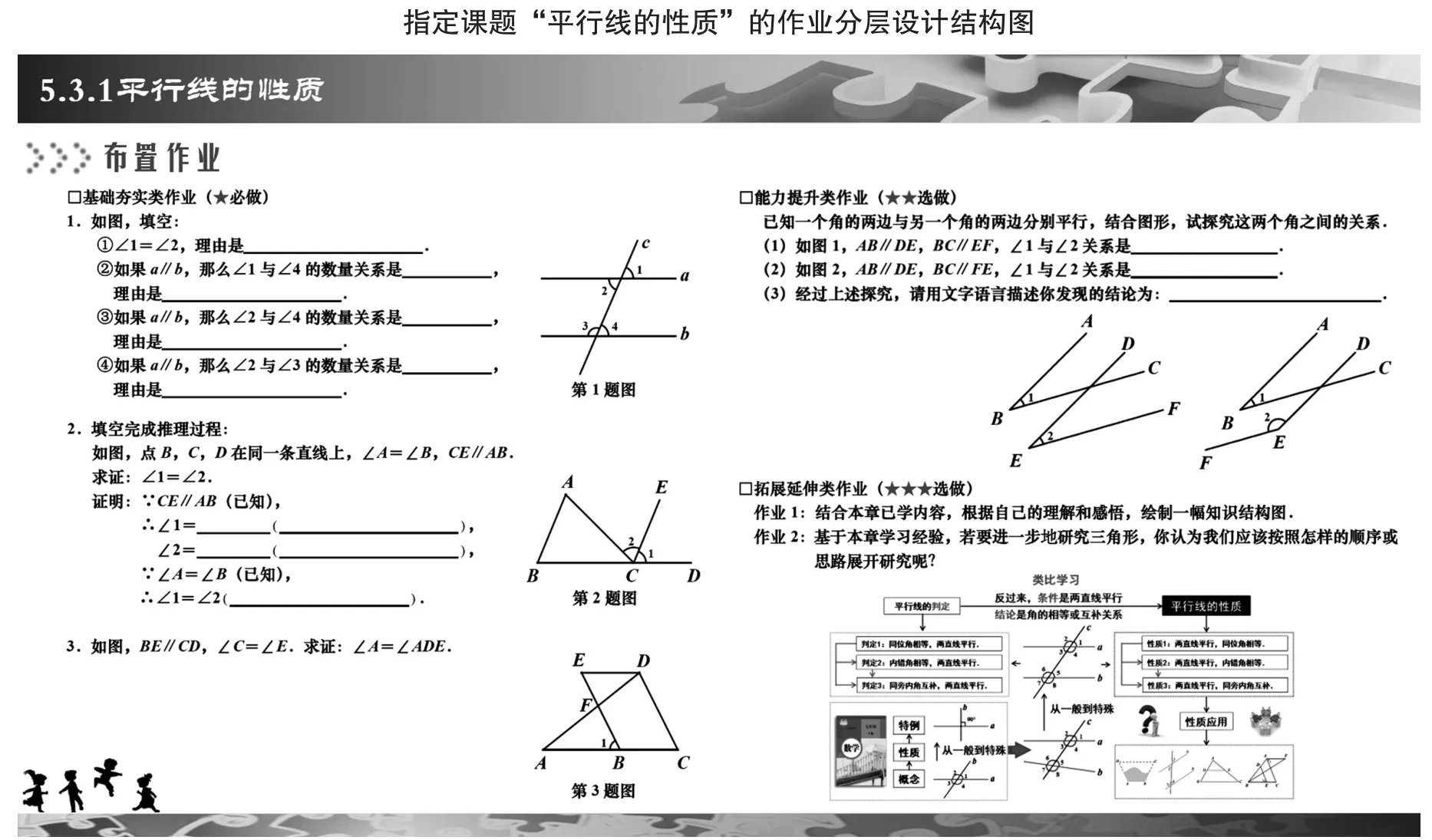
圖4

學生的精彩表現(xiàn)也給了我們意外驚喜.無論是教材內容的類比學習和分組學習的合作交流，還是課堂小結的相互質疑和作業(yè)布置的分層設計，都呈現(xiàn)了研究性學習的核心要素，既符合學生的認知水平，又激發(fā)了學生的學習潛能，培養(yǎng)了學生的創(chuàng)新意識，凸顯了學生的主體作用.

四、改進建議

教學是一門遺憾的藝術，也是不斷完善中的藝術.盡管本節(jié)課亮點頻現(xiàn)，但仍存在“三過”現(xiàn)象：學生探索過程過于流暢，推理論證過程操之過急，課堂小結過程過于單一.基于此，本節(jié)課仍可以從優(yōu)化“三觀”上進一步完善.

1.研究線索的整體觀可以進一步優(yōu)化

一是可以進一步通過整體性提升問題質量.數(shù)學家哈爾莫斯說，問題是數(shù)學的心臟.在基于“三線八角”回顧兩條平行直線判定方法的基礎上，可以提出如下更具有整體結構的正反兩個方面的問題.

問題1：“圖形的判定”討論的是確定某種圖形需要什么條件，那么“圖形的性質”需要研究什么問題？（研究這類圖形有怎樣的共同特性.）

問題2：根據(jù)平行線的判定方法，怎樣判斷兩條直線平行？怎樣判斷兩條直線不平行？（隱含著利用逆否命題轉換視角，導出平行線的性質.）

二是可以進一步通過可視化呈現(xiàn)研究過程.在利用整體設計呈現(xiàn)知識結構（如圖3）的同時，還可以通過聚焦學生的認知過程和思維過程可視化呈現(xiàn)平行線的研究路徑和學生數(shù)學核心素養(yǎng)的發(fā)展狀況.例如，可以用圖5表示平行線判定的研究思路（以角定線），用圖6表示平行線性質的研究思路（以線定角），最終整合成如圖7所示的“平行線判定與性質”的整體研究思路，既可以更直觀地總結研究過程，又可以更系統(tǒng)地呈現(xiàn)知識結構體系.

圖5

圖6

圖7

2.教學過程的育人觀可以進一步優(yōu)化

一是可以進一步突出研究過程的起承轉合.“平行線”是平面幾何圖形的重要基礎.在此，學生將初次進入幾何圖形系統(tǒng)研究的領域.此行，有著啟蒙、奠基與示范的作用.從相交線到平行線的類比思維，從判定到性質的逆向思維，思維的遷移和發(fā)散，在此處閃耀著理性的光芒.所謂見樹木，更見森林；見貝殼，更見大海；見平行線，更見幾何圖形，更見數(shù)學的神奇與美妙，更見數(shù)學思想方法的深邃與悠遠.同時，還可以將“三會”目標具體落實到平行線的學習之中——會用數(shù)學眼光觀察幾何問題，會用數(shù)學思維思考幾何問題，會用數(shù)學語言表達幾何問題.在這種一般觀念指引下進行幾何圖形性質研究，更有利于學生發(fā)現(xiàn)問題和提出問題，更有利于培養(yǎng)學生的應用意識和創(chuàng)新意識.

二是可以進一步展現(xiàn)研究起點的以退為進.“三線八角”模型特例應該是垂直截線的情形，因此探究的起點可以退到這種模型特例開始，這樣更符合從特殊到一般的自然切入，可惜的是本節(jié)課居然沒有這樣做.事實上，把問題回歸到原始狀態(tài)，可讓學生學到以退為進、逐步調整的方法和策略，養(yǎng)成良好的數(shù)學素養(yǎng).

3.訓練系統(tǒng)的價值觀可以進一步優(yōu)化

數(shù)學的內在力量，正在于其思想方法、訓練價值和育人功能的一脈相承.落實“四基”，提高“四能”，發(fā)展素養(yǎng)，是數(shù)學訓練系統(tǒng)（即對數(shù)學的例題、練習題、思考題、檢測題和作業(yè)題等的統(tǒng)稱）必須遵循的價值取向.盡管本節(jié)課的教學訓練系統(tǒng)設計比較精細，但仍存在個別題目的表述不夠嚴謹之處（如不能僅用圖示完全代替題干的條件描述）.因此，只有充分挖掘教材訓練系統(tǒng)的內在價值，把教學訓練系統(tǒng)設計成基于“四基”“四能”的探究性學習活動，才能更好地凸顯“雙減”政策背景下的作業(yè)設計質量，才能更好地發(fā)揮數(shù)學訓練系統(tǒng)的育人功能.

總之，真正高效的幾何課堂應該達到思想方法、幾何直觀和邏輯推理的高度融合，讓思想之光、直觀之魅和理性之美閃爍于教學的全過程，實現(xiàn)數(shù)學教學之獨特的育人價值.