基于理解設計高質量的學習活動
——對“角”一課的簡析

林祥華

（福建省廈門市教育科學研究院）

本節課所屬章為初中平面幾何的起始章，且內容較多，包括角的概念（兩種描述）、角的表示法、角的度量和單位換算、角的畫法等.其中，概念的抽象、幾何語言的應用等對于學生來說都具有一定的挑戰性.如何在有限的課堂時間內，突出重點，突破學生學習的難點，避免因內容多而導致的“趕任務、滿堂灌”，這在教學處理上是有難度的.

執教教師基于對教學內容和學生的理解，進行了頗具特色的教學處理.

一、亮點

本節課的最大亮點在于教師設計了高質量的學習活動.“高質量”主要體現在以下兩個方面.

1.概念形成的學習活動深度思辨

學生與角有關的學習經驗主要包括兩部分：一是小學階段對角的基于直觀感知的初步認識；二是本章對線段的較為系統的學習.對于學生，角的概念形成的難點在于：角的圖形的組成元素及元素之間的關系相對線段更復雜，定義的抽象性與嚴謹性要求更高.

那么，可以讓學生自己經歷角的概念形成過程給角下定義嗎？

以“角的靜態描述”為例，學生分別從實物中抽象三類角（鈍角、銳角、直角）的圖形后，執教教師提出核心任務“這些圖形有什么共同特征？請你給角下一個定義”，并設計以下學習活動.

教師先指導學生獨立思考，小組討論.教學視頻中，呈現了兩個小組的討論片段.

甲小組：

生1：我認為角應該是由一個點和兩條射線組成的圖形.

生2：我認為應該不需要說一個點，兩條射線組成的圖形就可以，只要端點重合在一起，就可以組成角.射線本身帶著端點，所以不需要說“由一個點”.

（同時用兩支筆演示.）

乙小組：

生3：角是由一個頂點發出的兩條射線組成的幾何圖形.

生4：先有角，這兩條射線重合的端點才可以叫頂點，所以只能說“由一個點發出的”.

在討論中，學生自然地關注到了角的組成元素、元素之間的關系，甚至關注到了表述的嚴謹性.

在展示、辨析環節，教師逐個展示了四個小組的結論，并讓學生進行辨析.

結論1：由兩條射線組成的圖形叫做角.

結論2：由兩條射線相交而成的圖形叫做角.

結論3：由端點重合的兩條射線構成的圖形叫做角.

結論4：一個點引出的兩條射線組成的圖形叫做角.

學生判斷結論1和結論2錯誤，并分別畫出反例的示意圖；判斷結論3和結論4正確，并分別說明了理由.

這四個結論不僅具有典型性，還體現了思維的層次性：在小組討論的基礎上，學生通過辨析錯誤結論、舉反例，對角的組成元素及元素之間關系的正確認識呼之欲出，再通過辨析正確結論、說明理由進一步深化認識，完成抽象概括的過程，此時凝練定義水到渠成.

接下來，是形成定義，總結方法.

執教教師在對定義進行解釋的同時，指出：“兩條射線”是角的組成元素；有“公共端點”指的是組成元素之間的位置關系，引導學生總結給幾何圖形下定義的方法：描述其組成元素及元素之間的關系.

上述學習活動在核心任務引領下，先放再收，環環相扣、層層遞進，始終緊扣概念的關鍵要素.在活動過程中，學生經歷了活躍、自主、深刻的思辨，對角的概念的認識由感性到理性，去偽存真，在理解概念的同時，感受了給幾何圖形下定義的一般方法.

通常，在概念教學中，我們會在概念形成后設計辨析練習.事實上，學生在概念形成過程中對關鍵要素進行充分辨析更為重要，也更有效.

雖然本節課內容較多，但執教教師在“角的靜態描述”和“角的動態描述”分別用時9分9秒、10分10秒（不含應用練習）.教師在時間上的“舍得”，使學習活動從容有序，為活動質量提供了很好的保障.

2.不同內容的學習活動多樣適宜

本節課不同教學內容的主要學習活動如表1所示.

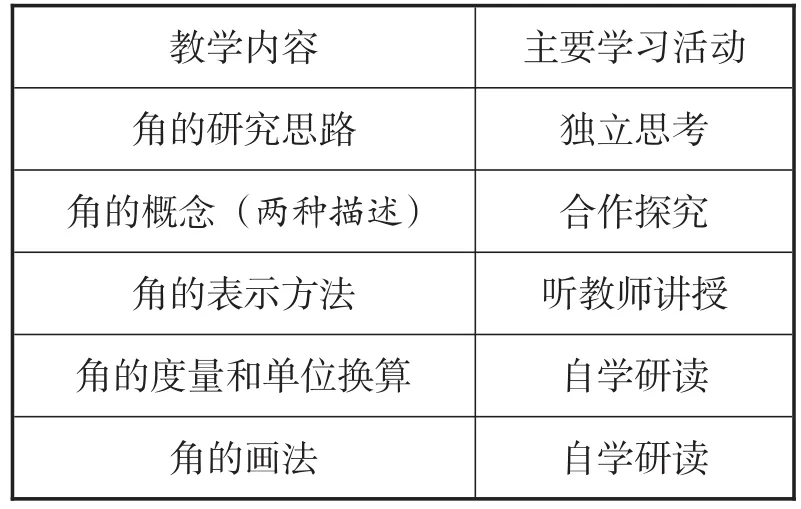
表1

可以看到，教師的活動設計充分考慮了與內容目標、學生認知水平的適切性和學習活動的多樣性.

（1）與內容目標、學生認知水平的適切性.

例如，對于構建角的研究思路，學生有關于線段的認知基礎.要求獨立思考是適切的.而獨立思考有助于學生更深刻地感受數學知識的整體性.

又如，角的度量與單位換算是一種規定，教材中對此有較大篇幅的閱讀材料，讓學生通過自學研讀了解相關的數學文化，知道角的度量與單位換算的由來，是符合內容目標與教材編寫意圖的.

（2）學習活動的多樣性.

多樣的學習活動使課堂生動活潑、張弛有度，銜接緊湊卻無壓迫感，充分調動了學生的學習積極性，尤其符合七年級學生的心理特征.

事實上，從教學視頻中可以看到，教師對于“學生是學習的主體和思維發展的主體”有強烈的意識，即使是自學研讀，也會組織學生交流、展示，讓學生自己總結閱讀方法.

二、思考

當然，一堂好課，在提供示范、予人啟發的同時，也會引發思考.下面就兩個方面做簡單探討.

1.關于銜接教學

在“角的動態描述”教學中，教師提出問題：“角這個圖形是否包含兩條射線之間的部分？”通過活動引導學生得到肯定的答案，并進行了強調.

事實上，到了高中階段，角的概念將擴展到任意角.任意角是由射線旋轉的方向和在該旋轉方向上的旋轉量進行刻畫的.有了任意角之后，以單位圓為工具，引入弧度制，將銳角三角函數推廣為任意角三角函數，借此可研究周期變化現象.

因此，從角的旋轉方式形成的角度認識角，主要目的是引導學生認識到：角不能僅僅簡單看成“有公共端點的兩條射線”，還應該注意到兩條射線的相對位置.實際上該相對位置是由始邊到終邊旋轉的方向和角度確定的，鑒于學生尚未學習旋轉的方向和角度，可以引導學生關注射線旋轉過程中掃過的區域，從而感受射線在旋轉過程中的位置變化.過于強調“角這個圖形包括兩條射線之間的部分”，將來對角的概念進行擴展時可能會受認識上的局限.

對于不同學段都會學到的知識，需要我們更多地關注知識的銜接教學，了解不同學段的相關內容及其教學目標有何不同，從而基于聯系把握教學的“入口”與“出口”.

2.關于類比推理

在構建角的研究思路的教學中，教師提出問題：“類比線段的研究思路，結合小學時角的研究內容，角將學習哪些內容呢？”

在教學中，我們通常會提出類似問題，引導學生基于數學知識的整體聯系發現、研究新知.但就本節課而言，學生的相關認知經驗還很單薄，線段與角的圖形、度量單位在他們看來相異甚大，兩者可以進行類比研究并非順理成章.

類比是一種推理方式，與歸納推理都是合情推理.在歸納推理的教學中，我們會強調基于一類對象的共同特征或特定規律下結論.但對于類比，往往很少“講道理”.事實上，類比推理是一種或然性推理，提高類比推理的可靠程度需要考慮兩個方面：一是類比對象的相同點要盡量多，這樣兩者關聯度越大，結論就越可靠；二是相同點與推出的結論都應指向本質.也就是說，在進行類比推理之前，至少需大致感受類比對象之間具有某些本質上的相同點，從而感受“為什么可以類比”，之后才解決“如何類比”.這樣有利于學生合理應用類比推理，發展數學推理素養.

因此，我們可以進一步思考：如何向學生滲透線段與角具有某些本質上的共同點？何時滲透？上述“類比線段構建角的研究思路”的問題何時提出更為適宜？

三、結束語

從總體上看，本節課教學目標的達成度高，執教教師教態自然親切，善于營造良好的課堂氛圍，巧于激發學生積極主動的數學思考，聽來從容沉穩、如沐春風.尤其是活動設計中所反映出來的對數學、教學、學生的理解，充分體現了教師優秀的教學素養，本節課是一節非常值得借鑒和學習的好課.