情境引導·問題驅動·方法提煉
——“有理數乘法法則”教學實踐與思考

崔 娜

（貴州省貴陽市觀山湖區外國語實驗中學）

一、背景分析

由小學的算術數到初中的有理數，是數系的又一次擴張.而“引進一種新的數，就要研究相應的運算；定義一種運算，就要研究相應的運算法則、運算律”，這是代數的核心思想.在數系、運算法則和運算律中獲得的知識，是可以遷移到后續代數學習中的，這體現了有理數運算教學的思維訓練價值.

從本章來看，有理數乘法的學習，類比有理數的加法，既是有理數運算的進一步深入，又是學習有理數的除法、乘方的基礎.本節課也較好地體現了類比、分類討論等數學思想方法，為學生抽象能力、運算能力等數學核心素養的發展提供了豐富的載體.

從學情來看，學生已有的認知經驗是小學算術范圍內的乘法運算，有理數的加、減法運算，學生也具備一定的觀察、分類、對比、歸納、總結等能力.但是，學生對含負有理數的乘法法則的探究和歸納存在一定的困難，這就需要教師組織一些數學活動，予以引導.七年級學生的思維處于從以具體形象思維成分為主向以抽象邏輯思維成分為主的轉折期，所以在呈現教學內容時必須注意具體性、形象性，還要有適當的抽象、概括要求.因此，本節課的教學重點是經歷有理數乘法法則的形成過程，運用有理數乘法法則進行計算；教學難點界定為“負負得正”合理性的探究.

二、教學實踐

1.情境引入，自主探究，發展數學抽象能力

情境：水箱是生活中常用的存儲水的工具，在蓄水時，某水箱水位每天升高2個單位長度；排水時，該水箱水位每天下降2個單位長度，取標準水位作為0點.

問題1：在蓄水時，1天后水箱水位的變化量是多少？2天后呢？3天后呢？你能嘗試把計算水位變化量的過程列成數學算式嗎？

有學生利用加法算式表示，也有學生利用乘法算式表示.

追問1：你能解釋這些式子的含義嗎？

追問2：這兩組算式有什么關系呢？

學生解釋算式中各數的實際含義，教師點撥加法與乘法之間的關系，做出“用正號表示水位上升，用負號表示水位下降”“用正號表示幾天后”等規定.

問題2：沒進水時，水位的變化情況可以列成類似的算式嗎？

學生嘗試列式，教師適時點撥、引導，板書算式.

問題3：在蓄水時，1天前水箱水位的變化量是多少？2天前呢？3天前呢？你能嘗試把計算水位變化量的過程列成數學算式嗎？

追問：觀察以上算式，你能解釋這些式子的含義嗎？

學生繼續解釋算式中數的實際含義，教師點撥，并完善“用負號表示幾天前”的規定.

自主探究：類比前面三個問題，請同學們獨立完成以下問題，然后組內交流探討.

問題4：在排水時，1天后水箱水位的變化量是多少？2天后呢？3天后呢？你能嘗試把計算水位變化量的過程列成數學算式嗎？

問題5：沒排水時，水位的變化量可以列成類似的算式嗎？

問題6：在排水時，1天前水箱水位的變化量是多少？2天前呢？3天前呢？你能嘗試把水位變化量的過程列成數學算式嗎？

教師展示學生所列算式，學生充分表達觀點，解釋算式含義，教師繼續糾正學生所列算式中的錯誤.

教學分析：為了使學生充分感受數學與實際生活的聯系，發展學生的抽象能力，本節課由生活中水箱蓄水、排水的情境逐步引出有理數乘法的前三種類型（正數乘正數，0乘正數，負數乘正數）.借助幾何畫板軟件的動態操作，引導學生理解乘法算式中因數、積的實際意義.通過自主探究環節，學生獨立完成最后三類乘法算式（正數乘負數，0乘負數，負數乘負數）的抽象.一方面，充分調動學生的主動探究意識，完善有理數乘法的幾種類型，繼續從生活中抽象算式，體會算式的含義；另一方面，學生充分體驗知識的生成過程，為學生探究“負負得正”的合理性積累活動經驗，也為后續法則的歸類及探討做好鋪墊.

2.“問題串”引導，提升“四能”，突破難點

深入探究：

追問1：觀察以下算式，它們的結果正確嗎？

1 × 2=2； 1 ×（-2）=-2；

2 × 2=4； 2 ×（-2）=-4；

3 × 2=6； 3 ×（-2）=-6；

0 × 2=0； 0 ×（-2）=0；

（-1）× 2=-2； （-1）×（-2）=2；

（-2）× 2=-4； （-2）×（-2）=4；

（-3）× 2=-6； （-3）×（-2）=6.

追問2：兩個負數相乘，結果是正數，你能找到合理的解釋嗎？

追問3：水箱水位變化的情境，你能給出合理的解釋嗎？

教師在學生思維有困惑處點撥，演示水箱模擬圖，在情境中給“負負得正”以合理的解釋.再引導學生調整算式順序，等待學生再觀察、再發現.

追問4：觀察這些算式，它們還有什么內在規律嗎？

追問5：改變一下這些算式的位置，你能發現數的變化規律嗎？

學生逐步發現積的變化規律，從而發現其中一個因數從正因數遞減1變成負因數的過程，學生逐步由算式中因數和積的變化規律解釋了“負負得正”的合理性.

教學分析：教師適時提出問題串，在學生的困惑處啟發學生逐步深入思考，充分交流，學生由小學學過的正數乘正數、0乘正數開始展開思考，逐漸發現積與其中一個因數的變化規律，進而明確了對“含有負數的兩數相乘之積符號的認識”，達成本節課的教學目標，突破了本節課的教學難點.尤其，在負負得正合理性解釋的過程中，從生活情境中抽象數學算式，又由數學算式尋找實際含義和規律探索兩種解釋，豐富了學生的思考維度.

3.歸納應用，體會思想方法，發展運算能力

法則歸納：（1）你能給以上算式歸類嗎？說說你的理由.

學生由積的符號或由因數的符號兩個角度進行歸類.

（2）你能嘗試歸納有理數乘法法則嗎？

生1：同號得正，異號得負，任何數與0相乘，都得0.

生2：同號得正，異號得負，并把絕對值相乘.任何數與0相乘，都得0.

（3）師生完善法則：兩數相乘，同號得正，異號得負，并把絕對值相乘.任何數與0相乘，積仍為0.

鞏固提升：

（1）計算：8×（-3）.

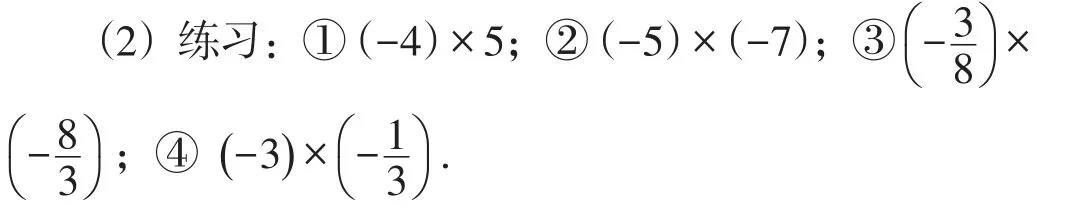
（3）歸納：在有理數范圍內，乘積是1的兩個數互為倒數.

（4）總結：有理數乘法運算的一般步驟，即有理數相乘，先確定積的符號，再確定積的絕對值.

教學分析：為了發展學生觀察、歸納、總結等能力，采取引導學生觀察有理數乘法算式，探討不同的分類標準，再嘗試歸納有理數乘法法則的方法.學生逐步形成對因數的符號與積的符號、因數的絕對值與積的絕對值關系的雙重認識，同時滲透分類、歸納等數學思想方法.為了檢測學生的學習效果，規范解答，教師示范一道題以后，讓學生完成四道題目的計算，并查漏補缺，形成對有理數乘法運算步驟上的共性認知，發展學生的運算能力.

4.及時反思，建構知識體系，提煉一般方法

（1）通過本節課學習你有什么感悟（如圖1）？

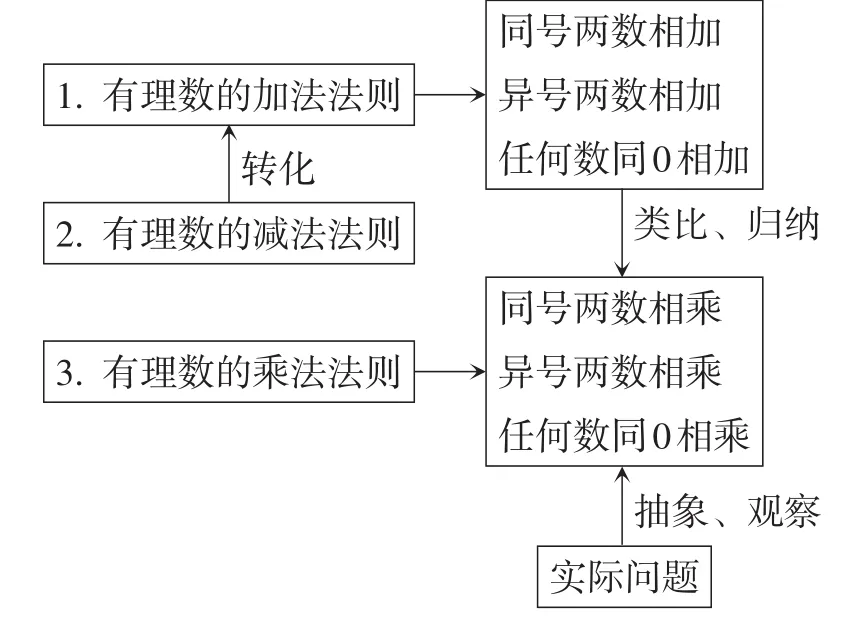
圖1

（2）你還想了解什么？還有哪些疑問？

教學分析：引導學生回顧定理，加深對定理的理解，思考、歸納定理的方式、方法，重知識、更重探究法則的一般方法的提煉，體現運算法則的一致性.在總結的過程中，注重培養學生及時反思的好習慣，引導學生學會學習，堅定學好數學的信心.

三、教學思考

1.在運算教學中，嘗試以情境引導

有理數乘法有別于有理數加法，在“負數乘負數”情境的選擇上存在兩個方面的困難：一方面，現實背景不易尋找；另一方面，對學生的抽象能力和理解能力要求比較高，這些都給有理數乘法背景的尋找增加了難度.以水箱蓄水、排水以及幾天后、幾天前為情境，解決兩個方向的問題.由情境可以得出有理數乘法的所有類型，給學生充分的生活視角和相對全面的問題，學生完整經歷數學算式抽象的全過程，逐步落實數學核心素養，啟發學生“用數學的眼光觀察現實世界，用數學的思維思考現實世界，用數學的語言表達現實世界”.

2.在運算教學中，重視以問題驅動

具有各自功能價值的問題，依據特定的內在聯系、有機組合而成的問題串，既反映一節課的教學內容，又能完整體現一節課的“骨架”，更是啟發學生深入思考、探究的重要路徑.課堂教學是否成功很大程度上取決于問題或問題串的設計.好的問題可以激發學生的學習興趣，啟發學生思維，幫助學生理解.本節課在“負負得正”合理性的探討中，通過問題串逐層深入探究，學生既能從實際情境中尋求合理解釋，又能通過因數的規律變化進行不完全歸納.至此，學生完成了由實際情境抽象得到算式，再由算式回到情境或者用數的變化規律解釋合理性的全部思考，進而突破教學難點，同時提升了學生分析問題、解決問題的能力.

3.在運算教學中，突出一般方法的提煉

在課堂上，學生除了掌握數學知識和方法，還應該明確研究數學問題的一般路徑和方法，這是較為重要的，從生活情境抽象數學算式、由數學算式討論合理解釋、發現一般規律，類比有理數的加法，概括有理數乘法法則，體現了研究數學運算法則的一致性和一般觀念，學生才會發現問題并提出問題，才會找到探究數學結論的方向.在教學中，幫助學生形成數學的整體觀，能夠站在一個較高的角度認識本節課內容的意義，這一點尤為重要.引領學生在數學課堂上，體會數學的本質、感悟數學思想方法、形成數學核心素養，為社會培養創造性人才！