直線光柵伺服系統自抗擾控制仿真分析與實驗研究

黃小津，胡超迪，魏 巍，李加勝

（1.機械制造工藝研究所中國工程物理研究院，四川 綿陽 621900）（2.上海交通大學機械與動力工程學院，上海 200240）

1 引言

在工程實際中，往往可以通過消除誤差來實現系統的控制，而其中的一個關鍵問題是采用何種方式抑制各種不確定的外部擾動對系統控制的影響。PID控制的核心思想是基于誤差的反饋控制，控制算法將輸出信號采集，并與輸入信號作差，然后將該誤差作比例、積分、微分后進行線性相加組合，得到被控對象的控制信號。

文獻[1]提出了基于PID進行改進和創新的自抗擾控制技術，它繼承了PID控制的主要思想，即狀態誤差反饋，又克服了其系統快速響應與容易產生超調之間的矛盾，并擁有線性誤差反饋所不具有的特點，更具有其獨有的擾動估計補償的核心思想。自抗擾控制方法提出后，已經有眾多的學者、工程師展開了大量的理論研究與工程應用。

文獻[2]根據Lyapunov 函數思想研究了擴張狀態觀測器（ESO）的誤差，并列出提高其估量精度的參數所應滿足的條件，研究了存在干擾條件下系統穩態誤差的范圍以及在無干擾條件下穩定的充分條件。

文獻[3-4]深入研究了不同非線性因素下自抗擾控制系統的收斂性，分別基于單輸入單輸出和多輸入多輸出非線性系統進一步證明了在閉環條件下的收斂程度。文獻[5-6]詳細分析了描述函數法對包含非線性自抗擾控制系統的極限環。文獻[7-9]分析研究了Lyapunov穩定性、絕對穩定性以及描述函數法的極限環對自抗擾控制系統穩定性的影響。目前，自抗擾控制技術已經在控制領域，特別是針對一些擁有非線性，大擾動，模型不確定等特性的控制系統，有了大量的研究與應用。文獻[10]研究了自抗擾控制技術在冷軋生產過程中的應用。文獻[11]研究了自抗擾控制技術在微機電換能器上的應用。文獻[12]研究了自抗擾控制策略的球磨機制粉系統，通過理論與實驗證明了自抗擾控制算法具有較好的抗干擾性以及魯棒性。文獻[13]研究了自抗擾控制技術在AUV航向控制中的應用。這類應用的特點是系統未知、為非線性、會受外擾等多種因素影響。

為直線伺服平臺設計了自抗擾控制算法，通過數值仿真研究了該算法中一些參數對直線伺服平臺控制性能的影響，比較了在系統中自抗擾控制算法與傳統PID控制算法對階躍響應以及常值干擾的控制效果。基于matlab仿真與實驗，對比分析了自抗擾控制算法與PID控制算法抗干擾性能和優缺點。在自抗擾控制實驗中，對直線伺服系統實現了模型辨識與自抗擾控制，觀察自抗擾控制下的階躍響應并在加入模擬常值干擾后觀察系統響應，對自抗擾控制算法能迅速抑制干擾進行了研究。

2 自抗擾控制

對外部擾動進行估計并據此進行補償是自抗擾控制原理的精髓所在。一般的自抗擾控制器的結構，如圖1所示。自抗擾控制通常由四個部分組成：根據輸入信號安排合適中間過程的過渡過程安排部分、可以估計系統狀態并估計擾動的系統擴張狀態觀測部分、線性或者非線性的狀態誤差反饋部分和根據估計的擾動進行補償的擾動估計補償部分。

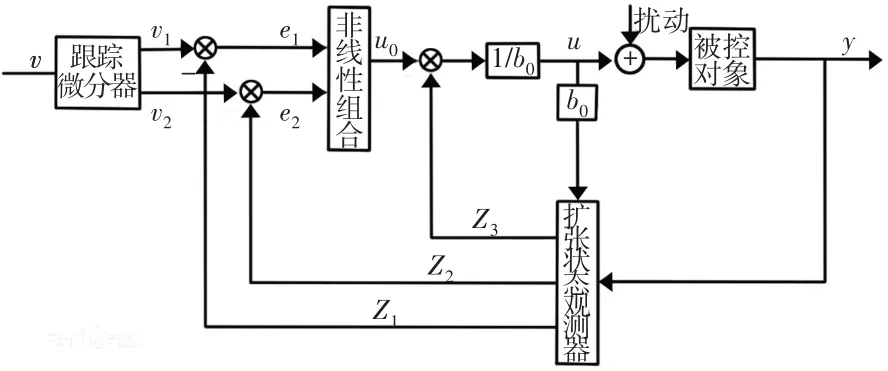
圖1 自抗擾控制框圖Fig.1 Block Diagram of ADRC

2.1 狀態誤差反饋

反饋機制是受控系統特征。反饋機制能在一定范圍內使系統性能按人的意愿得到改善，負反饋機制還具有一定的抑制微小擾動的作用。由前文可知自抗擾控制器的狀態誤差反饋接收的誤差是設定值的誤差以及其微分的誤差，相當于實現PD 控制。傳統的線性PD控制的誤差反饋律如下所示：

式中：u0—輸出的控制量；e1、e2—控制量誤差以及其微分誤差；β1、β2—參數。

除了線性的狀態誤差反饋形式之外，還有很多非線性的形式可以采用，參考文獻[1]對不同的非線性形式做了大量分析，證明適當的非線性反饋比線性反饋效率高很多。文獻[6]提出了如下一些非線性形式的狀態誤差反饋：

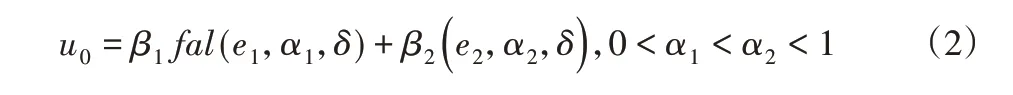
式中：α1、α2、β1、β2、δ、r、h1、c—參數；函數fal(e，α，δ)可表示成：

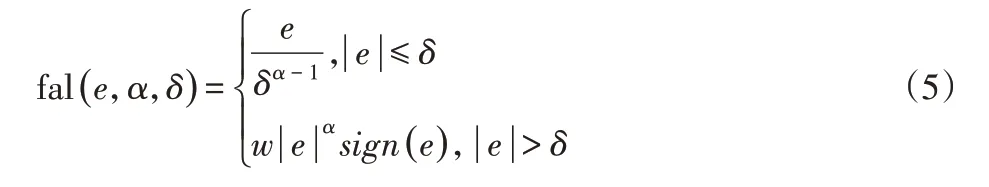
采用使用非線性反饋式（4）作為反饋控制律。

2.2 擴張狀態觀測器

在反饋控制系統中，負反饋對外界擾動有一定的抑制作用。而在自抗擾控制，就是利用擴張觀測器通過系統的輸入輸出來對擾動進行精確的估計，根據擾動的估計值進行前饋補償從而消除擾動影響的控制方法。

擴張狀態觀測器借用了狀態觀測器的思想，把能影響被控輸出的擾動當作新的狀態變量來觀測，根據控制系統的輸入與輸出信息，估計出系統狀態變量與這個新的狀態變量。擴張狀態觀測器的結構圖，如圖2所示。

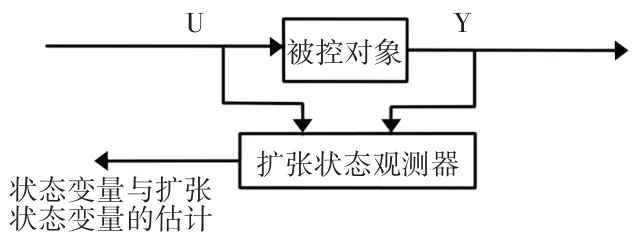
圖2 擴張狀態觀測器框圖Fig.2 Block Diagram of Expansion State Observer

對于如式（6）所示二階系統，系統原有狀態變量x1，x2，現將f(x1，x2)擴張為狀變量x3，若設f(x1，x2)的導數為w(t)，則擴張后的系統變成式（7）。

式中：x1，x2—系統狀態變量；b—系統固有參數。

對于式（7）所示的狀態方程，可建立如下離散形式的狀態觀測器，只要選擇好參數，該觀測器z1、z2、z3能很好地分別估計狀態變量x1、x2、x3。

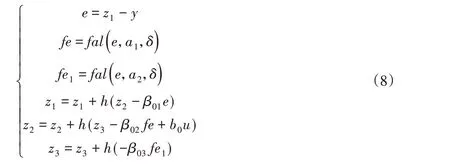
式中：δ、β01、β02、β03、a1、a2—參數。

關于這些參數的整定，參考文獻[1]給出了說明，z3估計f(x1，x2)的誤差，z2估計x2的誤差，z1估計x1的誤差的大小分別約為為f(x1，x2)的大小，可估計其最大值計算。那么只要取得β03足夠小于w0，β02、β01取得足夠小，理論上就能獲得一個小的穩態估計誤差。

3 自抗擾控制仿真分析

為說明自抗擾控制的優勢，將模擬控制一個一維直線運動平臺，對同一個二階系統分別采取自抗擾控制和傳統PID控制進行仿真。仿真中調整自抗擾控制中各項參數如下：

1.r0=1e6；h0=5e-4；%安排過渡過程參數；

2.r1=0.5/h^2；h1=5*h；c=0.05；%非線性組合參數；

3.β01=1/h；β02=3.3e-1/h^2；β03=1e-3/h^3；δ=h；a1=1；a2=1；

%擴張狀態觀測器參數；

4.b0=1e7；%擾動補償參數；

5.k=1e7；b=100；a=50；%二階系統參數。

仿真中調整PID控制中各項參數如下：

1.P=5e-5；2.I=2.5e-9；3.D=1e-5。

3.1 階躍響應分析比較

兩種控制方法有相似的位移曲線，如圖3所示。在當前參數下，兩者都沒有超調，且兩者過渡時間相近。可以發現，PID控制的響應在該參數下較快，但隨著穩態誤差的減小，糾正速度逐漸降低，最終達到接近穩定的狀態反而沒有自抗擾控制快。自抗擾控制的相應曲線上看，該曲線幾乎以直線靠近階躍輸入設定值，快速的同時沒有超調。事實上，可以比較兩種控制的速度變化曲線來更細致地分析。兩種控制方法的速度曲線，如圖4所示。

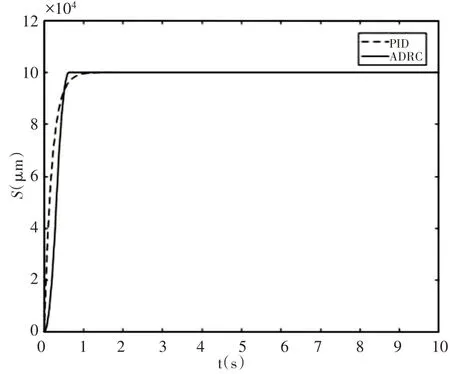
圖3 PID與ADRC的階躍響應Fig.3 Step Response of PID and ADRC

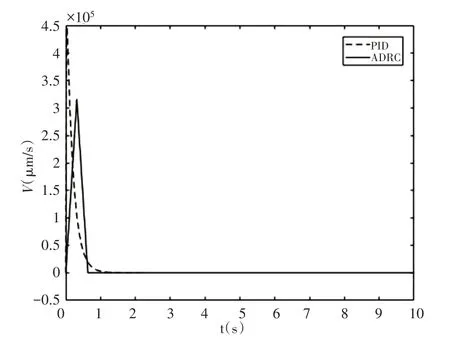
圖4 ADRC和PID階躍響應的速度Fig.4 Velocity of the Step Response of ADRC and PID

可以看出，PID方法的速度一開始產生了較大的跳變，這種跳變是不合理的，可能會對運動系統造成影響或者較大的速度超出系統能達到的范圍。而圖4中自抗擾控制方法的速度曲線在初始時基本上呈現等邊三角的形狀，這是受到安排過渡過程的作用形成的設定速度曲線，相比PID控制可以看出其最大速度更小。因而可以認為自抗擾控制的響應軌線比傳統PID控制更合理。

3.2 抗干擾能力分析比較

自抗擾控制的核心內容和優勢所在是控制方法的中的干擾估計和補償，對自抗擾控制和PID控制抗干擾能力的分析比較可以說明其抗干擾能力的強大。

仿真將在第5s時兩種控制方法下所控制的二階系統的輸入值中增加幅值不同的常值干擾和低頻正弦干擾，觀察兩種控制方法下的最終輸出響應來比較其抗干擾能力。

在第5s時加入常值干擾后兩種控制方法下系統的輸出，如圖5所示。加入的干擾值為1V、0.5V、0.1V，圖中可以看出，PID控制對常值干擾是有一定的抑制作用，但是抑制作用很差，恢復時間已經基本超出了圖中5s的范圍。而在干擾小于1V的范圍內，自抗擾控制的輸出基本不受干擾的影響，在圖中已經無法看出。在加大干擾后，自抗擾控制的輸出，如圖6所示。

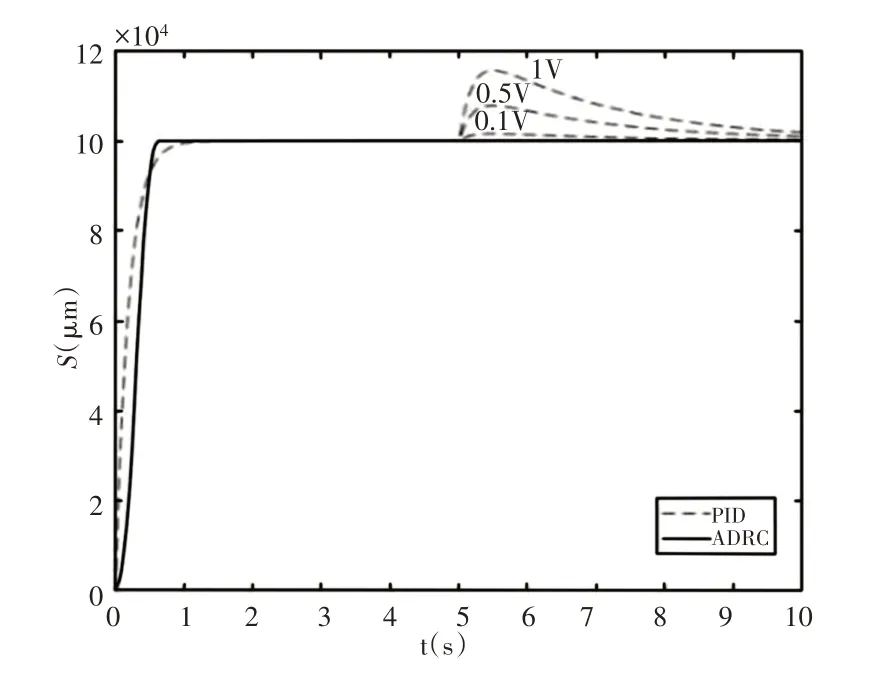
圖5 ADRC與PID常值擾動下的響應Fig.5 Response of ADRC and PID with Constant Disturbance

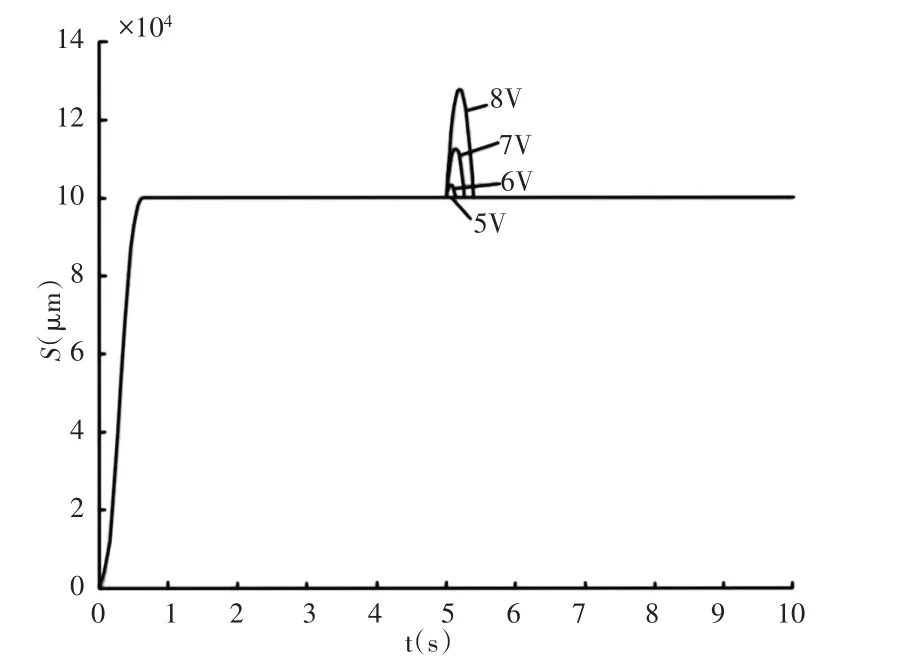
圖6 ADRC更大常值擾動下的響應Fig.6 Response of ADRC with Lager Constant Disturbance

系統的輸出在5V干擾下仍未產生明顯的影響，在干擾繼續增大后才產生比較明顯的影響，但在干擾量為8V的作用下時，系統恢復設定值的時間約為0.5s左右，比圖4中PID控制的恢復時間短很多。因此，從可控干擾的大小和恢復跟蹤設定值的時間上來看，自抗擾控制比PID控制都有較大優勢。

自抗擾的參數較多，過大或過小的參數選擇會引起系統不穩定、產生超調或者響應、抗干擾能力減弱等情況。但很多參數的選擇范圍都比較大，整定較為容易，可以根據文獻[1]建議的參數做適當調整來確定參數。

4 自抗擾控制實驗

選用的直線運動平臺設計，如圖7所示。主要包含：直線電機、大理石底座、氣浮軸承及平臺導軌、光柵等。整個運動平臺將被置于一氣浮隔振臺上，以減小環境振動的影響。

圖7 直線運動平臺實物圖Fig.7 Picture of Linear Motion Platform

4.1 伺服系統辨識

伺服系統的辨識能了解系統特性，以更好地控制系統，在之后自抗擾控制中也可以根據辨識所得的系統選擇合適的參數。為辨識該二階系統，實驗輸入3 V的常值控制信號，通過NI Compact測量系統記錄系統輸入與同步的系統開環輸出，即系統的階躍響應。系統輸出，如圖8所示。

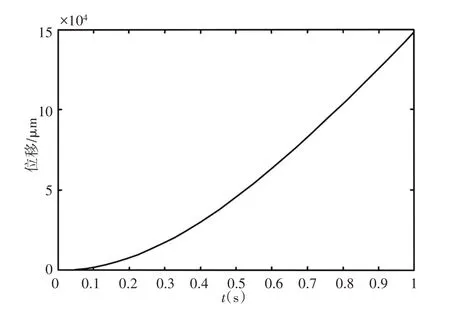
圖8 系統階躍響應Fig.8 Step Response of the System

利用matlab系統辨識工具箱對改輸出與3 V常值輸入進行傳遞函數辨識，模型為2極點0零點，得傳遞函數如下式（9）所示，擬合度達到了99.85%，可以認為建模與辨識是準確的。

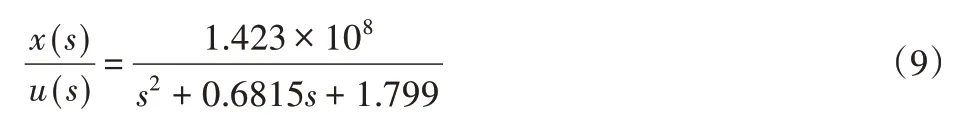
3.2 實驗結果

自抗擾算法參數選擇文獻[1]，針對二階系統提出的參數做了微調，其中b0為1.423×108，狀態非線性反饋參數中，為了減小位置誤差，參數C減小2個量級。在實驗參數的自抗擾控制下，伺服系統的105μm階躍響應，如圖9所示。系統響應與仿真結果基本符合，在該參數下略有超調。基本穩定后存在噪聲和震蕩，穩定后的截取一秒內的誤差，如圖10所示，均方根值較大，達到了0.5μm。

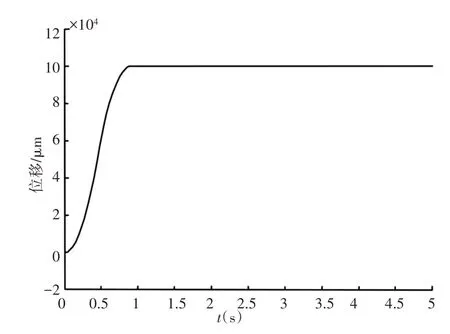
圖9 伺服系統階躍響應Fig.9 Step Response of the Servo System

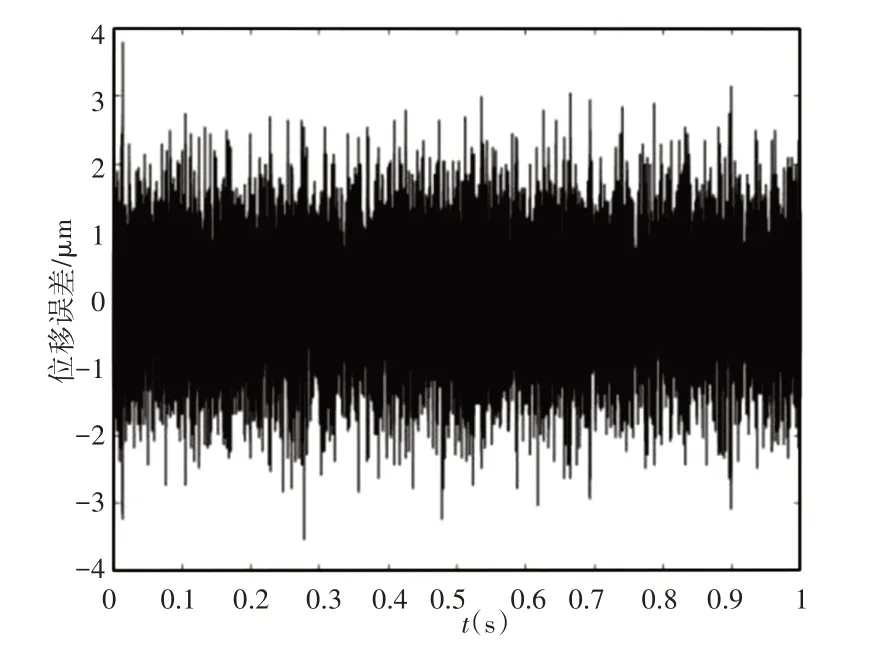
圖10 穩定后的誤差Fig.10 Error After Being Stable

實驗中，使用模擬添加常值干擾的方式，干擾常值分別是0.1 V、2 V，結果如圖11、圖12所示。

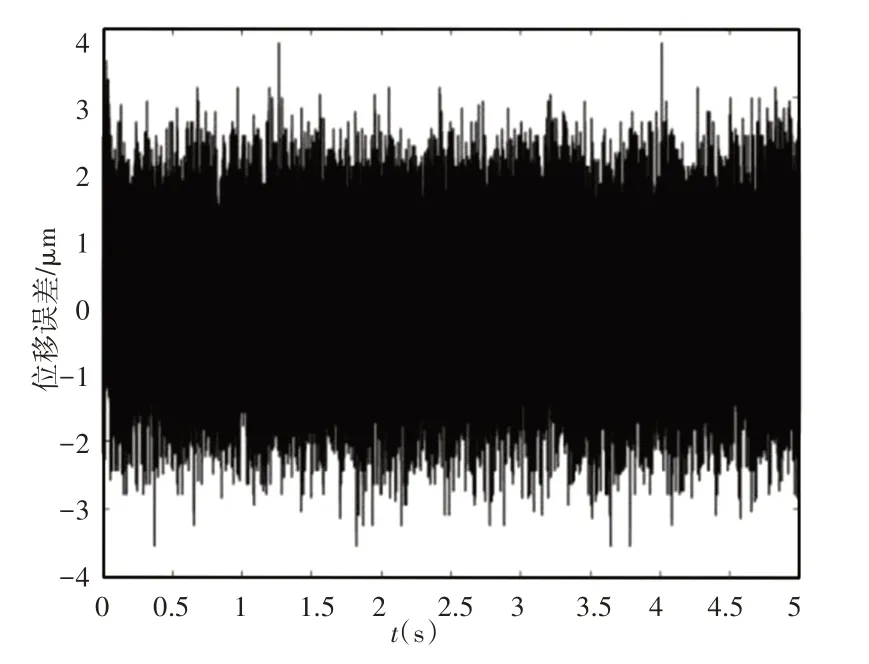
圖11 0.1V常值擾動下響應Fig.11 Response of 0.1V Constant Disturbance

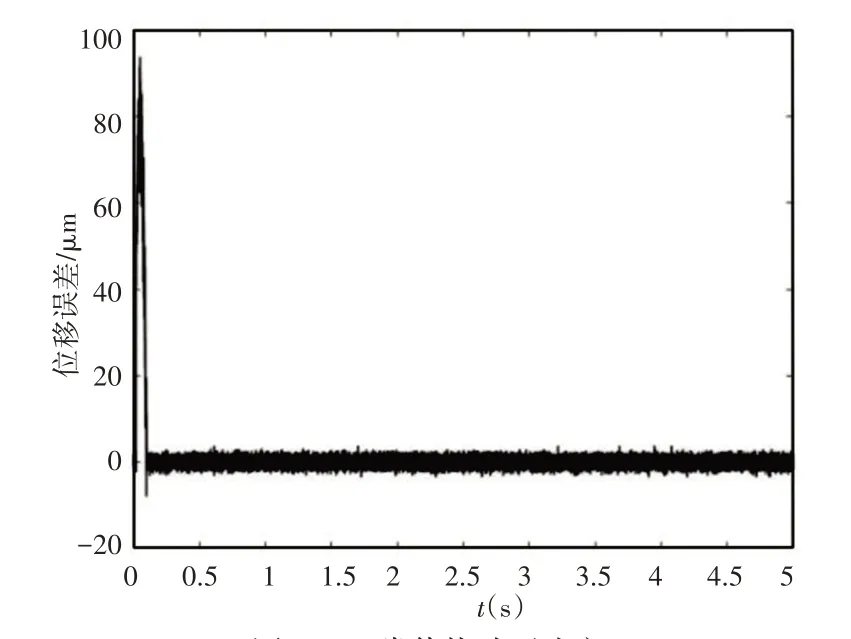
圖12 2V常值擾動下響應Fig.12 Response of 2V Constant Disturbance

圖中0時刻為擾動加入時刻。圖中可以看出，在0.1V時幾乎看不出影響，一方面也是因為噪聲過大。在2V時，可以看出出現一個尖峰，隨后回到穩定狀態，所用時間分別為0.1s左右，產生的最大偏差為20μm、95μm左右。可以看出，自抗擾控制具有對常值擾動的抑制作用，擾動越大，誤差變動越大與恢復時間越久。

5 結論

針對直線伺服平臺二階系統設計了自抗擾控制算法，基于基本的自抗擾控制算法，采用了最速控制綜合函數形式的非線性狀態誤差反饋；擴張狀態觀測器的系統輸入為控制器直接輸出，即最后將系統轉化為積分串聯型。根據Matlab仿真結果，通過與PID控制算法比較來驗證自抗擾算法的可行性和優勢，比較包含了階躍響應和常值干擾影響下系統的性能，自抗擾控制對比PID控制有如下優勢：對階躍響應能平衡快速響應與無超調，對常值擾動的抑制能力明顯更強。在自抗擾控制實驗中，對直線伺服系統實現了模型辨識與自抗擾控制，觀察了自抗擾控制下的階躍響應并在加入模擬常值干擾后觀察了系統響應，結果顯示。自抗擾控制能迅速抑制干擾作用。