一種面向葉片的機器人拋磨軌跡規劃方法

屈 展，劉 佳，楊勝強，郝曉偉

（1.太原理工大學機械與運載工程學院，山西 太原 030024；2.精密加工山西省重點實驗室，山西 太原 030024）

1 引言

隨著葉片類零件在工業中的需求不斷增加，現有的加工方式難以滿足其生產需求。工業機器人由于其多自由度且靈活多變的特點，逐漸被應用到葉片類零件的拋磨加工中。在機器人自動化拋磨葉片的過程中，拋磨軌跡的精度是影響葉片拋磨質量的重要因素。因此，高精度的拋磨軌跡至關重要。

傳統的機器人拋磨運動軌跡是通過在線示教編程得到的，對于葉片類零件來說，這種方法生成軌跡難度大、耗時長且滿足不了精度要求。目前大多采用離線編程的方式得到拋磨軌跡，通過處理CAD 模型生成拋磨軌跡，效率以及軌跡精度會大大提高［1-2］。文獻［3］提出了一種基于包圍盒思想的拋磨軌跡生成方法，采用包圍盒思想，引入機床表面銑削行切法，根據待加工模具的基本輪廓形象生成軌跡。文獻［4］通過基于CAD系統數據的自動規劃和編程系統規劃了機器人拋光路徑。通過Roboguide軟件在虛擬環境中對整個拋光系統實現在線控制。文獻［5］提出了一種基于Hilbert曲線的路徑生成算法，生成的路徑可以從多個方向通過自由曲面上的點且覆蓋密度是可調節的。文獻［6］等借鑒銑削加工中刀軌生成方法，提出一種機器人拋光自由曲面的軌跡規劃方法，利用等殘留高度算法生成拋光軌跡。

以上文獻中所采用的軌跡生成方法，均存在程序復雜，生成軌跡效率低的缺點。提出了一種機器人拋磨葉片的軌跡生成方法，采用基于三角網格模型的分層切片處理方法得到拋磨葉片的軌跡。并在傳統的分層切片算法的基礎上改進了交點追蹤方式，使生成的軌跡更加完善，效果更好。三角網格模型方法因其快速靈活、拓撲適應能力強，而經常被使用。基于STL數據模型的快速切片［7-9］算法，廣泛應用于復雜零件的快速成型系統。該算法亦可應用于工業機器人離線編程系統。

2 基于STL的分層切片算法

分層切片算法是采用一組平行平面，與工件的STL三維網格模型相交，根據分層平面與三角網格的相交情況，求取交點。根據三角網格間的鄰接關系，將所求交點依次連線，得到一條封閉的輪廓環，即拋磨路徑軌跡。軌跡生成原理，如圖1所示。

圖1 軌跡生成原理圖Fig.1 Schematic of Trajectory Generation

2.1 三角網格模型的建立

通過UG12.0建立葉片三維模型，提取葉片的STL文件數據，由STL文件數據生成三角網格模型。葉片的三維數據模型和三角網格模型，如圖2所示。

圖2 葉片模型Fig.2 Leaf Model

STL文件為一系列無序的空間三角面片的點數據集合。在讀取STL文件時，首先需要建立三角面片間的鄰接關系，并去除冗余點，具體的數據結構采用三角形網格鄰接表的形式。

三角形面片鄰接表主要記錄三角形號碼、毗鄰邊以及網格間的毗鄰關系。每個三角形面片都會相鄰有三個三角形面片，每一條邊都是由兩個三角形共享，稱為鄰接網格。找出文件中共享同一邊的每對鄰接網格，這樣就能建立鄰接表了。鄰接網格，如圖3所示。三角形網格鄰接表，如表1所示。

圖3 網格1、2的鄰接網格Fig.3 Adjacent Grids of Grids 1，2

表1 三角形網格鄰接表Tab.1 Triangle Mesh Adjacency List

2.2 分層平面與三角網格相交的判別與交點計算

按曲率變化方向對三角網格模型進行切片處理，如圖4 所示。用一系列平行的分層平面與三角網格相交（分層平面的分層方向沿垂直于葉片型面曲率變化大的方向），并進行求交計算。將分層平面與該層所有網格棱邊的交點進行連線，得到截面輪廓線，所有輪廓線構成的封閉圖形的集合，為拋磨葉片的軌跡。

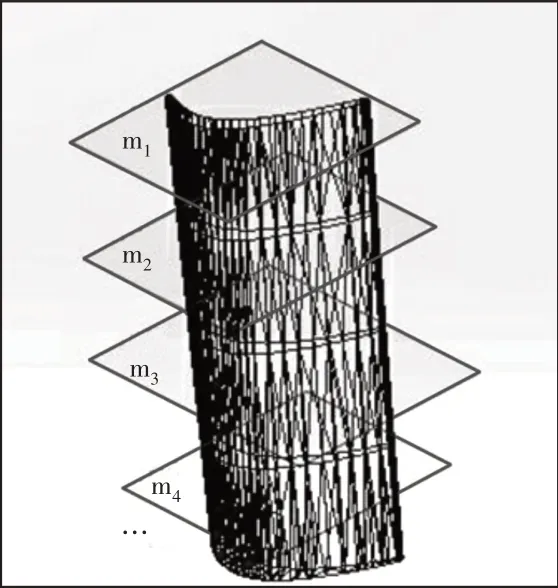
圖4 一組平行平面與葉片三角網格模型相交Fig.4 A Set of Parallel Planes Intersect with the TriangularMesh Model of the Blade

由于分層平面不能同時與一個三角面片的三條棱邊都相交，需要對三條棱邊中與該平面相交的兩條邊進行判別，如圖5所示。分層平面Z=mi與三角面（Z1，Z2，Z3）相交。

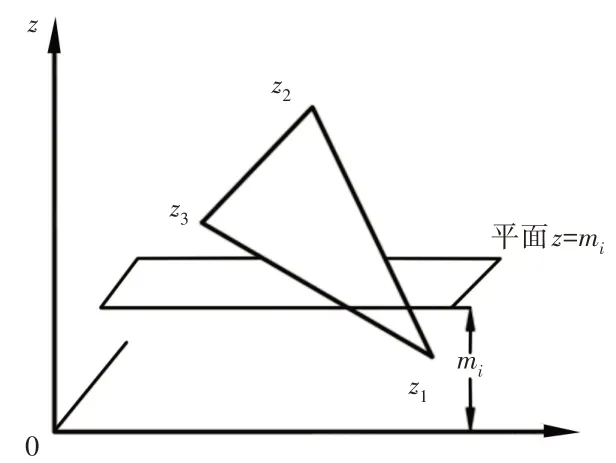
圖5 三角面片與分層平面相交的判別Fig.5 Discrimination of Intersection of Triangular Patch and Layered Plane

若mi≥mid（Z1，Z2，Z3），則與max（Z1，Z2，Z3）點連接的兩條棱邊與該平面相交；若mi≤mid（Z1，Z2，Z3），則與min（Z1，Z2，Z3）點連接的兩條棱邊與該平面相交。

其中max（Z1，Z2，Z3），mid（Z1，Z2，Z3），min（Z1，Z2，Z3）為三角面片三個頂點Z1，Z2，Z3的最大值、中間值與最小值。若分層平面與三角面片棱邊Z1，Z2相交，設Z1，Z2的坐標分別為（x1，y1，z1），（x2，y2，z2），則交點坐標可由直線方程確定。

求得分層平面與棱邊的交點坐標為：

同理，求出所有的相交點。

2.3 分層切片算法求加工軌跡

分層切片算法實際上是采用一組平行平面，與工件的STL三維網格模型相交，根據平行平面與三角面片的相交情況求取交點，然后根據三角面片間的鄰接關系，將交點連線，得到一條封閉的輪廓環，即拋磨路徑軌跡。

對葉片工件進行分層切片處理，需要確定分層的方向以及分層的間距△Z，然后以一系列間距為△Z的分層平面與三角面片相交并求取交點。分層方向沿垂直于葉片曲率變化大的方向，分層間距要小于三角葉片沿分層方向最大坐標值與最小坐標值的差值的最小值。假設三角面片沿分層方向的最大和最小坐標值分別為Zmax和Zmin。則分層厚度△Z＜min（Zmax-Zmin）。

每個分層平面與三角面片相交得到交點的集合，即｛p1，p2，p3，…，pm，pn｝。分層平面與同一個三角面片相交，一般情況下會有兩個交點（分層平面與三角面片的一個頂點相交時只有一個交點）點pm和pn。在求交過程中，對于一個分層平面Zi，首先計算第一個與該平面相交的三角面片，求出交點坐標。然后根據三角網格的鄰接關系找出相鄰的三角面片，沿垂直于分層方向正向追蹤交點（分層方向為Z向，垂直分層方向的正向為X正向），并將交點連線。訪問過的三角網格，通過標志label=1識別。直至搜索完所有的交點并連成線，形成一條封閉的輪廓環。得到這條軌跡后，標志重新改為label=0。如交點為三角面片的頂點，則按照點表搜索該頂點的三角網格鄰域，找到其他的交點并連線。然后將新找到的有交點的三角面片作為下一個起始的三角面片，按照前面的方法重新追蹤。

假如三角面片分布，如圖6所示。

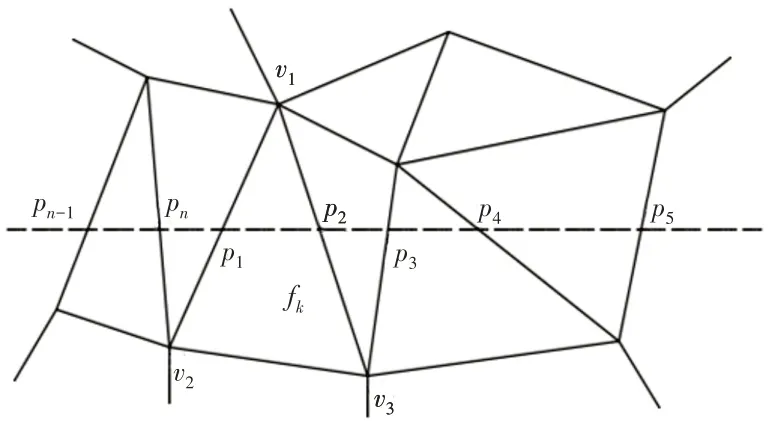
圖6 分層平面與三角面片相交的輪廓線示意圖Fig.6 Schematic Drawing of the Contour Line Where the Layered Plane Intersects the Triangle

計算過程首先根據三角面片數據文件的點拓撲鄰接關系計算與分層平面關聯的三角面片fk，然后通過對應三角形的頂點v1，v2，v3確定交線方程。得到交點集合｛p1，p2，p3，…，pn-1，pn｝。假如計算的第一個與分層平面相交的三角面片為fk。交點為p1和p2。沿垂直于分層方向正向追蹤交點并連線。假如三角面片分布，如圖7所示。

圖7 分層平面與三角面片頂點相交的輪廓線示意圖Fig.7 Schematic Drawing of the Contour Line Where the Layered Plane Intersects the Vertices of the Triangle

當前被處理的三角面片為fi，交點與三角面片的頂點重合，按照前面的方法找不到下一個待訪問的毗鄰三角形，此時交點為p4。通過點表，找到以v3為頂點的所有三角形面片，在這些三角形面片構成的鄰域內，除了正在處理的三角形面片fi上的兩個交點p3和p4外，只剩下一個交點p5，將p4和p5連線。并將三角面片fj作為起始三角面片，依次向后追蹤連線。

綜上所述，該切片求交算法求加工軌跡的完整流程圖，如圖8所示。

圖8 切片求交算法求加工軌跡流程圖Fig.8 Flowchart Flow Chart of Slice Intersection Algorith

3 機器人拋磨運動

3.1 機器人拋磨姿態的確定

在葉片的拋磨加工過程中，保證拋磨輪在拋磨點處始終與葉片型面保持最大接觸能夠有效的提高拋磨效果。當拋磨輪支撐軸方向沿接觸點的法向量方向，軸向沿最小主曲率方向，即拋磨輪軸向沿著與葉片工件最貼合方向，可實現工具與葉片工件的最大接觸［10］。葉片型面的主曲率與主方向可以做如下推導。葉片的STL文件中任一頂點vi的三角網格模型，如圖9所示。

圖9 葉片的STL文件中任一頂點vi的三角網格模型Fig.9 Triangular Mesh Model of any Vertex vi in the STL File of the Blade

三角面片fk的法矢Nfk的計算公式：

式中：ei—由頂點vi指向頂點vj的邊矢量；ei+1—由頂點vj+1指向頂點vi的邊矢量；頂點vi的法矢Nvi的計算公式：

式中：Ak—三角片fk的面積；rk—三角片fk在頂點vi處的內角。

對于當前點vi每個1-環鄰點vj，定義單位向量Tij是向量vj-vi在切平面?Nvi?⊥上的投影：

則，

是vi點處沿Tij的方向曲率。

除法向量Nvi為該矩陣特征值為0的特征向量外，另兩個特征向量T1，T2為主方向，特征值不是主曲率。主曲率為該矩陣的非零特征值函數。

主曲率方向拋磨姿態，如圖10所示。拋磨輪與葉片接觸于O點，調整拋磨輪以該姿態與葉片工件接觸，即拋磨輪支撐軸方向Zo沿O點的法向量方向，軸向方向Yo與T2平行，Xo與T1重合。

圖10 主曲率方向拋磨姿態圖Fig.10 Grinding Attitude Diagram of Principal Curvature Direction

3.2 拋磨機器人運動學逆解

機器人按軌跡拋磨，需知道機器人末端位姿以及各關節運動轉角。這就涉及到了機器人運動學正逆向求解的問題。建立機器人坐標系，通過建立機器人各個關節運動變換矩陣便可以實現正運動學位置和逆運動學求解計算，進而對機器人運動和姿態進行控制。 在機器人各關節建立的笛卡爾空間坐標系，如圖11所示。

圖11 機器人各關節坐標系Fig.11 Coordinate System of Each Joint of the Robot

機器人在笛卡爾空間坐標系中末端位姿信息可通過機器人運動學方程表示：

當已知機器人末端連桿位姿時，通過運動學逆向求解，得到各關節轉動的角度值，進而控制機器人末端到達指定位置和姿態。若末端連桿位姿已經給定，即n，o，a和p為已知，則求關節變量θ1，θ2，θ3的值稱為運動逆解。計算方法就是用轉換矩陣的逆矩陣左乘機器人運動學方程兩邊，根據矩陣元素對應相等，把關節變量分離出來，從而求解。

求得各關節角的值如下：

由以上求得的各關節角可知，對于機器人在同一個位姿處時，所求關節角會有多組解，并不是所有的解都能滿足機器人連續拋磨運動的條件，因此，需要在滿足機器人各關節在允許的運動范圍內，以各關節轉過的最小角度為標準，求出最優解。

4 機器人MATLAB運動仿真

為驗證所給參數的正確性，并得到機器人運動過程中各關節的運動位移，運動速度以及運動加速度，保證機器人運動平穩性，現基于Matlab Robotic Toolbox對機器人進行關節空間軌跡仿真。建立的機器人仿真模型，如圖12所示。

機器人在2s時間內，關節1到關節6的運動位移、運動速度、運動加速度變化圖，如圖13所示。

由圖13（a）中可以看出，關節1、3、4、6位移從零逐漸向正向變化，關節2、5位移從零逐漸向負向變化；由圖13（b）可以看出，關節1、3、4、6的運動速度是先增大后減小，關節2、5與之相反；由圖13（c）可以看出，各關節初、末加速度均為零，運動中出現兩次極值，且為一正一負。

圖13 各關節在2s內的運動變化Fig.13 Movement Changes of Each Joint in 2s

從圖中可以看出，該機器人的位移曲線平滑，速度和加速度曲線連續，說明在此工作過程中機器人運動比較平穩，無干涉現象發生，驗證了參數的準確性。

5 實驗驗證

為了驗證此拋磨軌跡規劃方法的有效性，對葉片進行拋磨試驗。由于葉片型面最大主曲率為0.0726，選擇拋磨輪半徑為10mm，拋磨輪轉速為1500r/min，機器人拋磨進給速度為低速，拋磨深度為0.5mm，采用基于STL分層切片算法生成軌跡，切片分層厚度為2mm，所對應的拋磨軌跡圖，如圖14所示。

圖14 基于STL切片算法的拋磨軌跡圖Fig.14 Grinding Trajectory Map Based on STL Slice Algorithm

拋磨前后分別選取葉片表面12個點，使用粗糙度儀分別進行粗糙度（Ra）檢測。拋磨葉片效果，如圖15所示。

圖15 葉片拋磨效果對比圖Fig.15 Comparison of Blade Grinding Effect

其中圖15（a）為拋磨前，平均粗糙度為2.017μm；圖15（b）為拋磨后，平均粗糙度為0.936μm；結果表明采用STL 分層切片算法生成拋磨軌跡。

6 結論

（1）采用基于三角網格模型的分層切片處理方法得到葉片拋磨的軌跡。通過CAD/CAM技術建立葉片的三維模型，生成葉片的STL三角網格模型。

對該模型進行分層切片處理，根據三角面片沿分層方向的最大和最小坐標值，確定分層厚度。推導分層平面與三角面片相交判別以及交點計算公式，將所求交點依次連線，最后得到拋磨運動軌跡。

（2）對機器人末端進行姿態的調整，保證拋磨輪在拋磨點處始終與葉片型面保持最大接觸。對機器人拋磨葉片進行了運動學逆向求解，確定了機器人各關節轉動角度，保證了機器人拋磨運動的準確性。

基于Matlab Robotic Toolbox對機器人進行關節空間軌跡仿真，可以看出機器人運動平穩，無干涉現象發生。按此拋磨軌跡進行實驗，拋磨效果明顯，表明了此軌跡規劃方法的可行性。