組合式陸空兩棲機器人的運動規劃與仿真

李凱林，韓寶玲，羅慶生，朱 琛

（1.北京理工大學機械與車輛學院，北京100081；2.北京理工大學機電學院，北京100081）

1 引言

為了在復雜地形下順利遂行多種偵查作業，靈活對多變的環境條件，將飛行器和足式機器人的優勢相結合的陸空兩棲機器人應運而生，且已成為國內外學者研究的熱點[1-2]。文獻[3]研發的HyTAQ Robo（tHybrid Terrestrial and Aerial Quadrotor），將四旋翼和籠罩相結合，空中飛行采用四旋翼模式，地面運動則通過調整飛行器的姿態使籠罩滾動。文獻[4]研發了一款海陸空全方位機器人，該機器人由四旋翼飛行器和兩個滾動輪式保護架組成，四旋翼實現飛行功能，通過輪式保護架滾動實現行走。文獻[5]研發了一款海陸空通用機器人MUWA，該機器人由四個變距螺旋槳和一個外圍環組成。上述提及的這些機器人其飛行器與地面機器人是一體的，無法分離單獨工作，而且地面機器人上沒有速度和加速度傳感器，無法精確控制移動，不能適應復雜的地面環境。設計了一款組合式的陸空兩棲機器人，使其兼具飛行器的靈活性和四足步 行機器人地面適應能力，既能實現結構分離，又能組合作業。

對于組合式陸空兩棲機器人而言，為增強對地面環境的適應性，四足步行機器人的運動規劃是尤為重要的。目前常用的步態規劃的方法有文獻[6]采用復合擺線作為擺動相足底軌跡，使用這種足端軌跡可以使足端在落地時的沖擊為零。文獻[7]通過橢圓足底軌跡得到了機器人對角運動步態，滿足實際樣機行走需求。而采用貝塞爾曲線為足端軌跡，讓機身進行勻速直線運動，使機器人實現walk步態。該方法在ADAMS仿真環境下獲得了較好的運動效果，進而驗證了規劃的可行性。

2 陸空兩棲機器人構型方案

2.1 結構特點

組合式構型方案是將四旋翼飛行器和四足步行機器人功能進行結合，使其兼具四旋翼飛行器的靈活性和四足步行機器人的超強地面適應能力。它們可以實現結構上的分離，分別執行陸空領域的偵察任務，同時四足步行機器人可以作為地面基站，四旋翼飛行器可以自由的起落在四足步行機器人軀體上進行組合作業，這既能準確控制四足步行機器人克服復雜多變的地面環境，又能同時進行陸空領域的偵查作業。三維模型，如圖1所示。

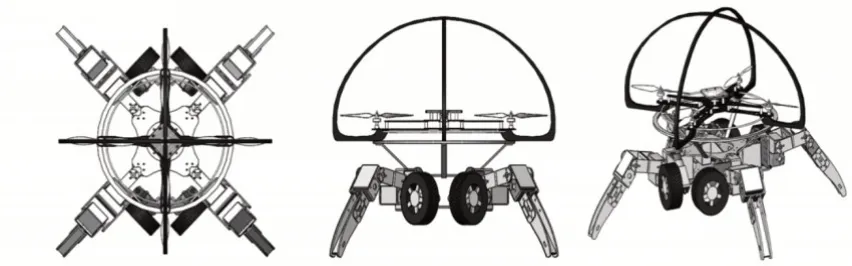
圖1 組合式陸空兩棲機器人三維模型Fig.1 A Three-Dimensional Model of a Combined Land and Air Amphibious Robot

四旋翼飛行器為標準的四旋翼無人機，機架為X構型的形式，考慮到四足步行機器人行走的速度問題，腿部采用輪腿復合式的結構，四條腿各配置一個自由度輪子，輪子分布在機器人的頭部和尾部，以保證機器人的足夠的足部運動空間。機器人的結構設計上依然沿襲了輕量化設計的理念，主體采用結構件，腿部零件在保證強度的情況下采用鏤空設計。

2.2 四足步行機器人的腿部構型

四足步行機器人腿部結構可以采用二自由度與三自由度兩種方案。二自由度單腿三維圖與結構簡圖，如圖2所示。采用雙搖桿機構，其中，ac段為機器人的小腿，桿cd和桿be共同構成了機器人的中間腿，大腿為三副桿def。d和f為主動關節，構成了該腿機構的兩個自由度。

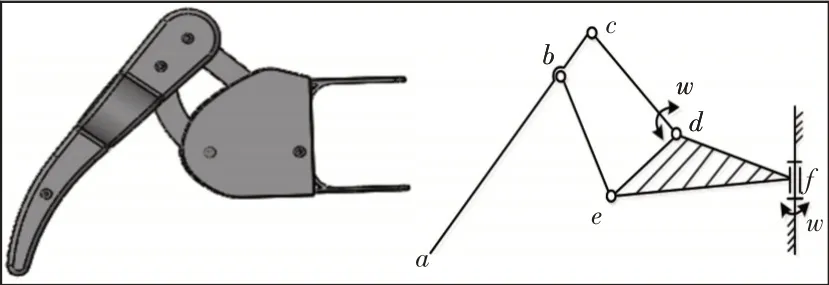
圖2 二自由度腿構型Fig.2 Two Degrees of FreedomFreedom Single Configuration

兩自由度腿機構可以實現機器人的大部分步態，但是兩自由度的腿機構足端軌跡相對固定，足端的可達域太小。它的靈活性相對較差，難以適應比較復雜的地貌環境。四足步行機器人需要和空中機器人協同作戰，以應對各種復雜環境，因此需要四足步行機器人工作空間大，運動靈活，顯然二自由度構型無法滿足要求。

采用三自由度腿部構型，機器人的髖關節，大腿關節和小腿關節各配置一個自由度，如圖3所示。其中d關節固定于機器人的機體上，決定機器人的腿前進方向的擺動，而關節b，c決定機器人腿側向的運動。三自由度腿機構相對于兩自由度腿機構，具有更豐富的足端軌跡，使得通過調整腿部的位置來調節機器人的重心的方法有更多的選擇，對于環境的適應能力更強。

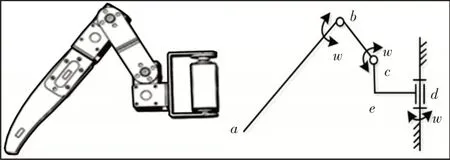
圖3 三自由度單腿構型Fig.3 Three Degrees ofLeg Configuration

3 足式機器人的運動分析模型

機器人的正運動學是已知機器人的各關節的類型，相鄰關節間的尺寸和相鄰關節相對運動量的大小，確定機器人末端在固定坐標系中的位姿[8]。根據機器人的構型方案，采用D-H法對機器人整體整機模型進行了腿2坐標系的建立。機身坐標系{b}位于機器人的機體質心，y軸為前進方向，腿關節坐標{C}位于側擺關節上，{W}為世界坐標系，如圖4所示。根據D-H參數表得到足端相對于機身的變換矩陣，進一步得到足端軌跡點的坐標，這就是正運動學求解。而逆向運動學是已知機器人末端在固定坐標系中的位姿，來確定每一個關節的變化量[9]。這可以通過幾何法或者在正運動學的基礎上的解析方法來進行求解。

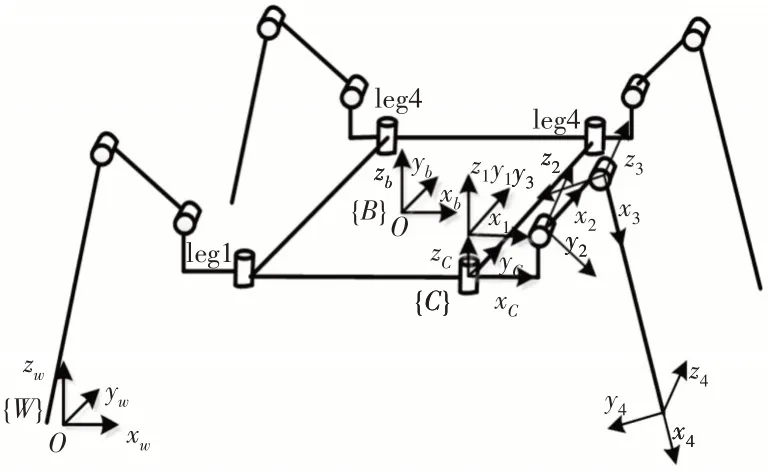
圖4 機器人運動學模型Fig.4 Robot Kinematics Model

4 地面機器人的運動規劃

4.1 步態規劃分析

運動規劃是保證機器人運動穩定性的關鍵技術，在機器人的研究中有著舉足輕重的地位.考慮到四足步行機器人屬于小型四足機器人，為了保證其運動的穩定性與流暢性，要求機器人可以在簡單的地形下慢速穩定的行走。因此選用靜步態，初步選定的步態為walk步態，所用的足端軌跡為貝塞爾曲線。

Walk步態規劃中把機器人三條腿的支點形成的三角形叫做支撐三角形，使用中心投影法（COP）作為機器人的穩定性判據，即當機器人的重心在地面的投影點落在三角形內時，則機器人是穩定的，不會發生摔倒。把中心投影點到三角形邊的距離的最小值叫做穩定裕度，穩定裕度越大，機器人越穩定[10]。當一個步序在運動中的任意時刻，機器人的穩定裕度都不為零時，認為該步序是穩定可行的。對于四足機器人而言，共有六種非奇異的靜步態邁步順序，在這六種邁步順序中，1-4-2-3 為穩定裕度最優的[11]。因而，在機器人的邁步順序中采用1-4-2-3的邁步順序。如機器人步序圖，如圖5所示。

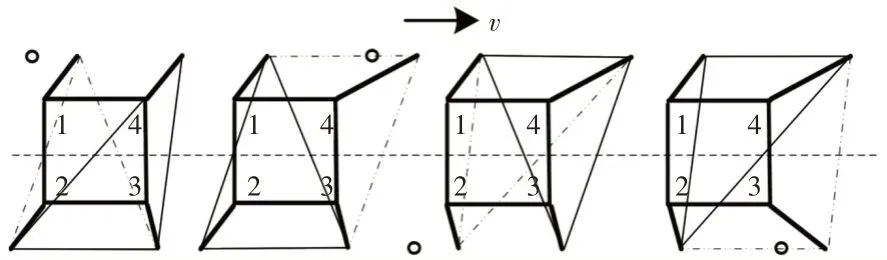
圖5 機器人步序圖Fig.5 A Sequence Diagram of a Robot

4.2 基于貝塞爾曲線的規劃分析

貝塞爾曲線最初是按照已知曲線參數方程來確定四個點，然后首尾連接成多邊形，接著通過貝塞爾公式逼近該多邊形，從而得到貝塞爾曲線[12]。它的方程如式中（1）所示。實際的規劃中采用插值法，即在貝塞爾曲線上選取一系列點，通過控制機器人的腿末端達到這些點即實現預期的規劃。插值點的密集程度取決于規劃的精度要求和機載計算機的性能[13]。

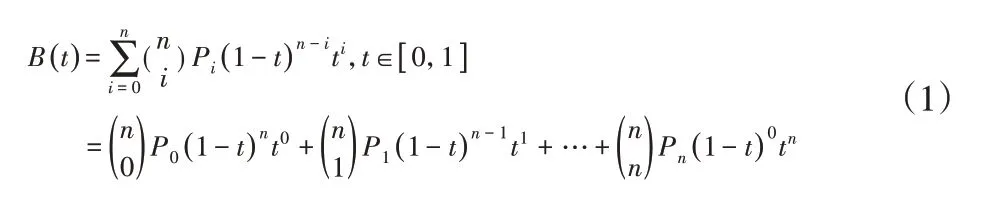
控制點兩點重合，產生零速度；控制點三點重合，產生零加速度（即零受力）[14]是貝塞爾曲線衍生方程的特點，在X和Y方向分量上，坐標相同的控制點對該方向速度分量同樣具有這樣的控制效果。

在軌跡中加入換向點，使足端按軌跡曲線運動時，盡量減小對機體的沖擊。從零點開始選用12個插值點坐標，如表1所示。它們可以滿足四足步行機器人足端接地時Y方向的速度分量為0，足端加速度盡量平滑，保證抬腿高度。

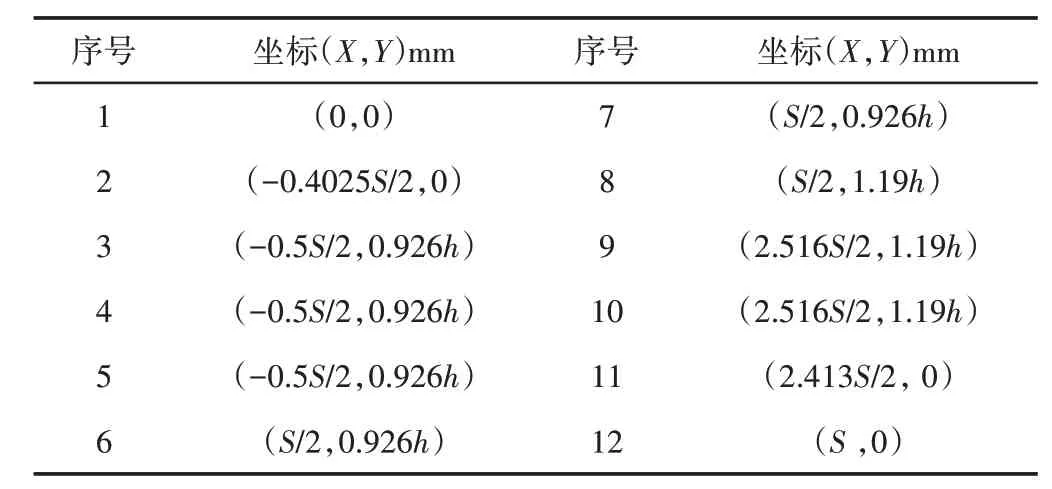
表1 貝塞爾曲線插值點Tab.1 Bayer Curve Interpolation Point

表格中S和h代表步長與步高，根據機器人設計方案，實際規劃中步行速度v=0.05m/s，步高h=0.05m，周期T=0.4×4=1.6s，S=vT=0.08m。各條腿與第一條擺動腿的相位差［b1，b2，b3，b4］=［0.25，0.75，0，0.5］，負載因子β=0.78，機身長L為2m=116mm，寬W為2n=116mm。各腿節長度為L1，L2，L3，各關節初始角度為θ1，θ2，θ3，具體參數，如表2所示。因此得到各條腿的足端軌跡方程如式（3）～（7）所示，機身軌跡如式（8）所示，生成的貝塞爾曲線及各插值點，如圖6所示。

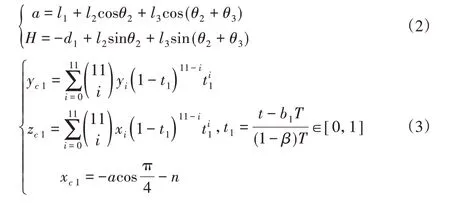
表2 步態參數Tab.2 Gait Parameter

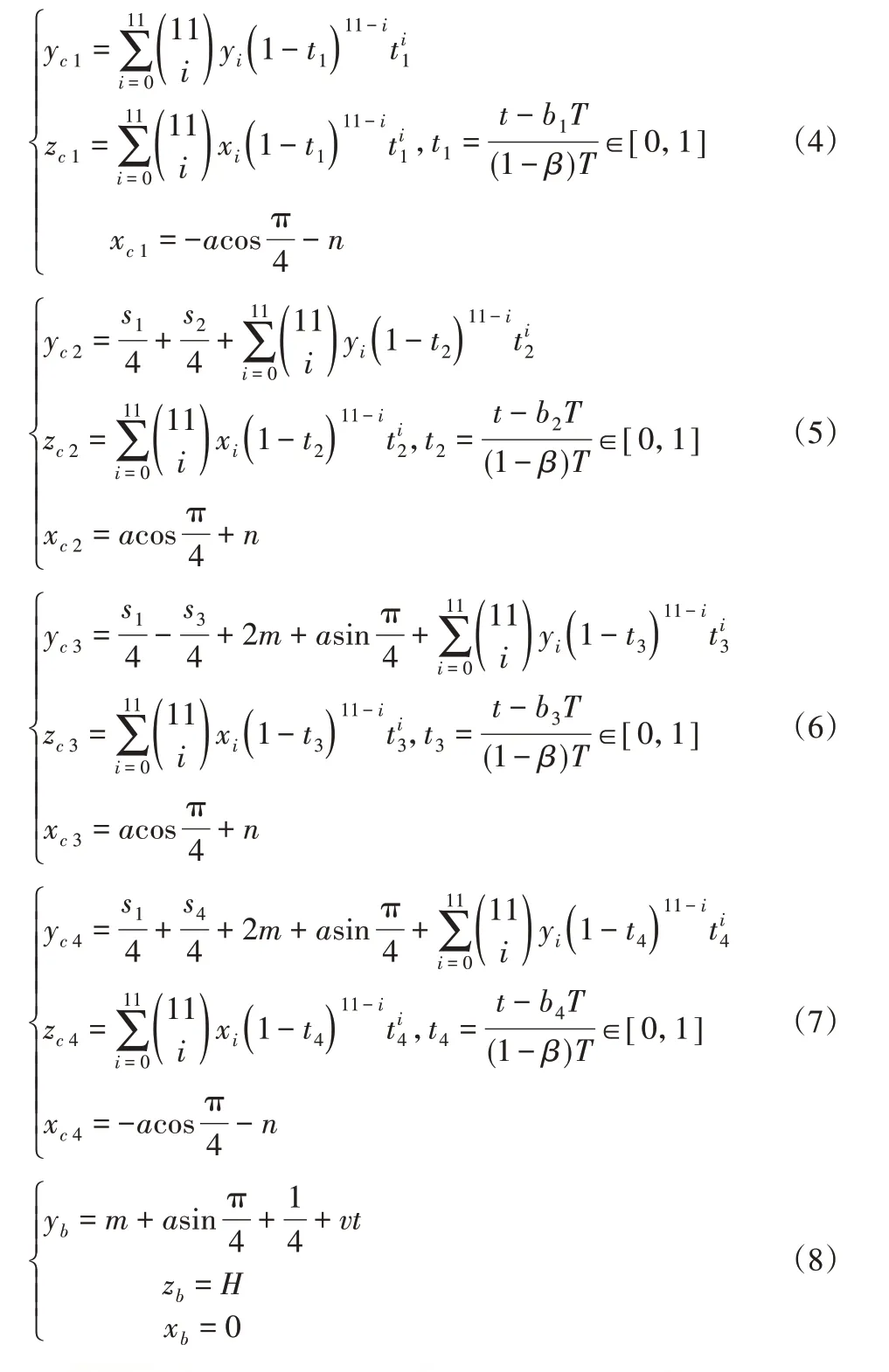
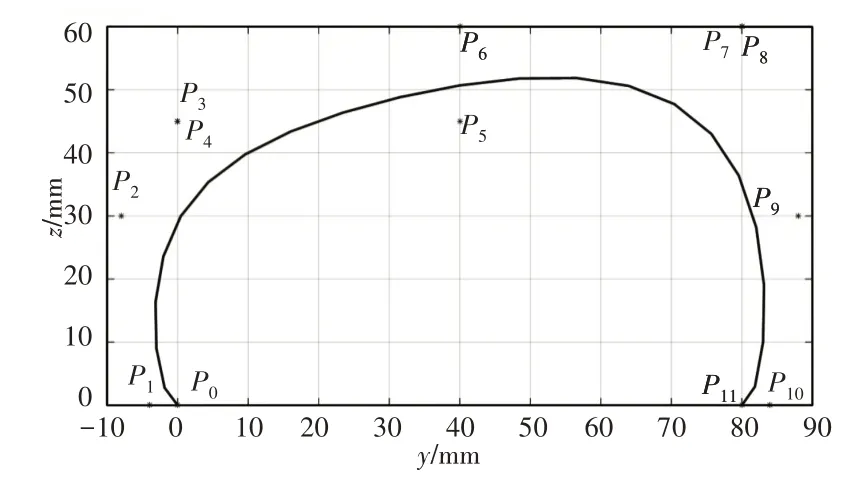
圖6 足端軌跡圖Fig.6 Foot Track Diagram

5 虛擬樣機建模與仿真

虛擬樣機技術是一種利用在計算機中建立的虛擬樣機代替物理樣機對產品進行設計測試和評估的方法，為了驗證通過貝塞爾曲線規劃得到的機器人步態的正確性，采用ADAMS 軟件建立機器人虛擬樣機模型，并進行仿真分析，所建立的模型，如圖7所示。

圖7 ADAMS模型Fig.7 ADAMS Model

通過仿真發現機器人可以穩定行走15個周期左右，其中前三個周期為準備階段，從第四個周期開始進入正常行進階段。通過分析仿真中機器人的機身位移和足端軌跡曲線，從而可以對機器人的穩定性和規劃的有效性進行評估。

規劃的機器人是勻速直線運動，因此最直接的觀察方式是觀察機身運動軌跡，機器人質心在X、Y、Z三個方向的位移，通過分析發現，機器人的位移曲線呈現鋸齒狀，這是因為在前進的過程中重心的變化產生了側翻轉矩，引起打滑現象導致曲線位移發生突變，如圖8～圖10所示。Y方向的位移曲線相對平滑，速度逐漸在加大，從4s之后，為一條斜率不變的斜線，對應的運動為勻速直線運動，且波動很小，說明機身沿直線前進。

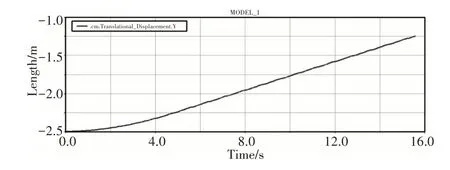
圖8 機身質心Y方向的位移Fig.8 Displacement in the Y Direction of the Fuselage

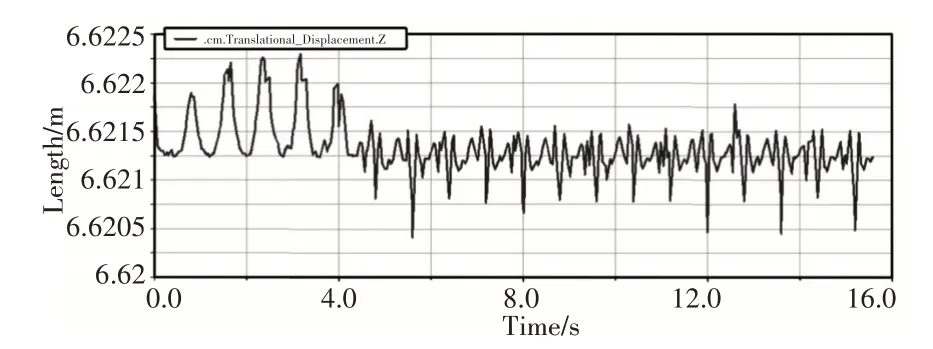
圖10 機身質心Z方向的位移Fig.10 Displacement in the Z Direction of the Fuselage

X方向平均偏移量為2.5mm，對于行徑的路程來說波動較小，說明機器人保持直線運動的穩定性較好。

Z方向的質心平衡位置偏移量約為0.5mm，主要是因為前三個周期是逐漸調整期，質心沒有達到預定的位置，穩定后質心變化呈規律性且平衡位置固定，說明機器人穩定性較好。

機器人腿1的足端軌跡圖，通過分析發現，足端位移在前進方向上和機身質心位移相似，不同之處是足端位移曲線有一些明顯的尖點，這是前進過程中存在沖擊的原因，如圖11所示。在z方向上機器人最大位移和步高吻合，進一步說明規劃是科學有效的。

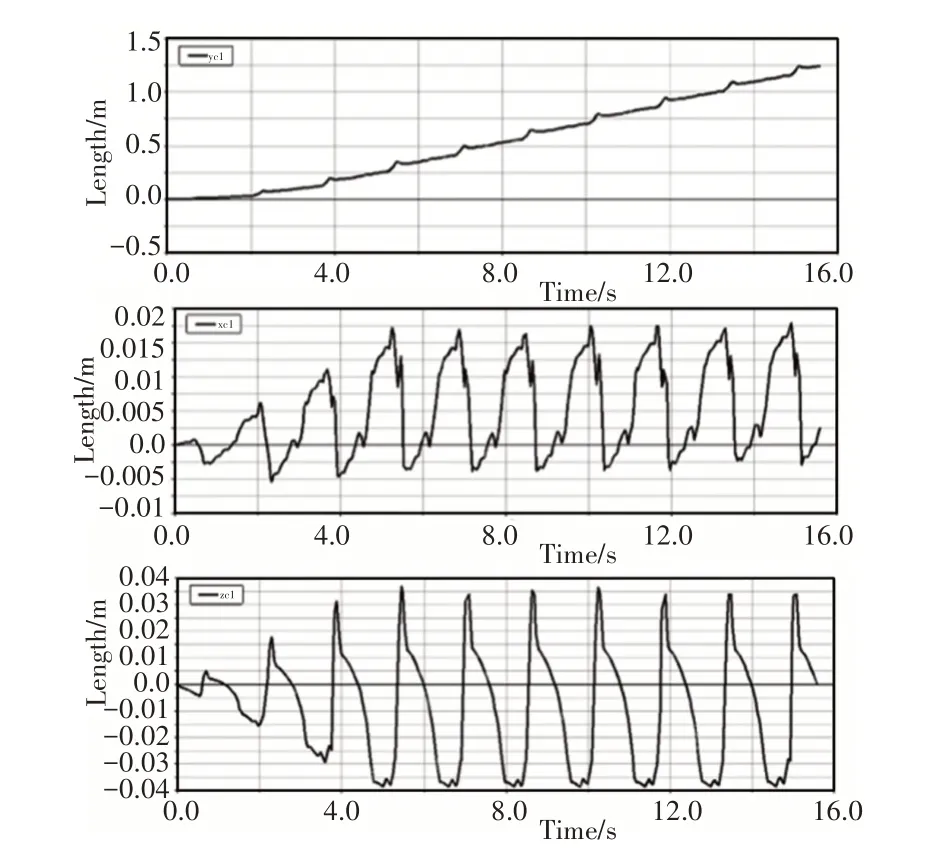
圖11 足端軌跡圖Fig.11 Foot Trajectory Map

6 總結

陸空兩棲機器人結合了四旋翼飛行器與四足步行機器人的結構特點，為多用途偵查提供了更多的可能性。

（1）機器人可分離的結構設計不僅大大增強了陸空兩棲機器人的環境適應能力，更為未來多樣化的設計奠定了堅實基礎。（2）足端軌跡采用貝塞爾曲線，規劃機器人按直線運動，通過運動學求解得到各關節位移曲線，用MATLAB 求得位移點轉化為驅動函數驅動虛擬樣機機器人進行了15個周期的連續運動，且步行運動的流暢性、穩定性與靈活性，驗證了該方法的正確性，并對物理樣機的控制提供了理論指導，具有推廣應用價值。