前饋控制加模糊補償的機器人關節角度追蹤

蒲明輝，趙倩倩，陳 琳，潘海鴻

（1.廣西大學機械工程學院，廣西 南寧 530004；2.廣西制造系統與先進制造技術重點實驗室，廣西 南寧 530004）

1 引言

機器人能將人類從眾多繁重的勞動中解放出來，主要原因之一是其可以按照人類規劃的關節角度運動[1-2]。機器人通過控制系統將規劃關節角度轉化為電機輸出的關節控制力矩，從而帶動其關節按照規劃角度轉動。但由于機器人模型存在不確定性，即理論參數不能精確測量得到以及實際工作過程中存在環境干擾等，導致機器人關節的實際運動角度和規劃角度之間存在誤差[3-4]。

為減小由于機器人模型不確定性造成的關節角度追蹤誤差，提高機器人的關節角度追蹤精度，研究人員提出了多種控制方法。

（1）PID控制方法：它不需要建立機器人模型，且具有較好的關節角度追蹤精度，在實際控制中得到廣泛應用。但其控制參數難以調節，需要較多的實驗進行調整和修改[5]；（2）自適應控制方法：它可以及時修正自己的特性來適應機器人建模誤差及外界環境干擾，但需要較為復雜的計算[6]；（3）魯棒控制方法：它可以實現對機器人不確定性的補償，不需要制定自適應律，實現較為簡單，但其指標的設定和權函數的選取過于依賴設計者的經驗[7]；（4）神經網絡控制和模糊控制等智能控制方法：這些智能控制方法具有高度的非線性自適應能力，可以實現對機器人未知部分的精確補償[8]。

以上方法有效減小了機器人不確定性造成的關節角度追蹤誤差，但各自也都存在一定的不足。為彌補上述控制方法的不足，進一步提高機器人的關節角度追蹤精度，研究人員將多種控制方法相結合。文獻[9]提出一種基于模糊控制的魯棒自適應軌跡跟蹤方法，在傳統自適應控制的基礎上加入模糊控制減小機器人關節角度初始誤差，并使用魯棒控制補償機器人模型的不確定性，實現了對不確定性機器人的有效控制。文獻[10]提出一種自適應神經變結構控制方法，采用徑向基函數神經網絡算法補償系統的不確定性，使控制系統具有較強的魯棒性。文獻[11]提出一種前饋和PID結合的控制方法，與傳統的PID方法相比，該控制方法魯棒性更強，且收斂時間較短。上述方法雖然取得了很好的成果，但仍存在一些問題需要完善。例如，其初始階段誤差波動較大，需要一定的時間才能使機器人的實際關節角度收斂到規劃關節角度。

針對上述問題，提出一種前饋控制加模糊補償的控制方法。前饋控制器利用機器人動力學模型獲得前饋關節力矩，模糊補償控制器獲得關節補償力矩，二者共同作用于機器人。利用ADAMS和Matlab/Simulink建立聯合仿真模型，并與前饋和PID結合的控制方法比較，驗證了所提出控制方法的可行性。

2 機器人動力學模型

機器人的關節力矩取決于機器人參數及其關節運動狀態，不考慮機器人建模誤差及環境干擾等不確定因素，利用Lagrange方法建立n自由度機器人標準動力學方程［6］：

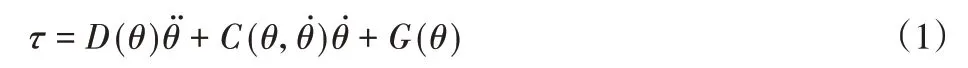
式中：τ—機器人關節力矩，τ∈Rn；θ、θ、?θ?—機器人的關節角度、角速度和角加速度，θ、θ、?θ?∈Rn；D（θ）—機器人的慣性矩陣，D（θ）∈Rn×n；C(θ，θ?)—機 器 人 的 離 心 力 和 科 氏 力 矩 陣，C(θ，θ?)∈Rn×n；G（θ）—機器人的重力矩陣，G（θ）∈Rn。

二自由度機器人控制是多自由度機器人控制的基礎，以二自由度機器人為例，驗證所提出控制方法的可行性，其簡化模型，如圖1所示。

圖1 二自由度機器人簡化模型Fig.1 Simplified Model of Two Degree of Freedom Robot

根據圖1建立二自由度機器人標準動力學方程，則式（1）中各部分表達式如下：

式中：τ1、τ2—關節1和關節2的力矩—關節1和關節2的角速度及角加速度；其它變量，如圖1所示。

3 控制系統

提出的控制系統包含前饋控制器和模糊補償控制器兩部分。前饋控制器輸出前饋關節力矩τd，模糊補償控制器輸出關節補償力矩τf，最終獲得機器人關節控制力矩τz：

3.1 前饋控制器

前饋控制器的作用是對下一運動狀態需要的關節控制力矩值進行估計，并使用該估計值對機器人進行提前控制，減小可能出現的誤差。由第2節可知，機器人的關節力矩與機器人的參數及運動狀態有關。將機器人的規劃關節角度θd、角速度和角加速度代入式（1）可獲得關節控制力矩的估計值，即前饋關節力矩，表達式為：

3.2 模糊補償控制器

為控制機器人按照規劃關節角度轉動，設計一種模糊補償控制器獲得關節補償力矩對前饋關節力矩進行補償，如圖2 所示。首先，利用模糊控制［12］獲得關節力矩補償系數；然后，該補償系數與前饋關節力矩τd相乘得到關節補償力矩τf，如式（7）所示。

圖2 機器人控制框圖Fig.2 Control Block Diagram of Robot

式中：u—關節力矩補償系數；e—關節角度誤差，e=θd-θ；ec—關節角度誤差變化率，即關節角速度誤差，ec=θ?d-θ?。

圖2中，模糊控制的輸入量為e和ec，輸出量為u，采用三角形隸屬度函數對輸入量和輸出量進行描述，將模糊論域分為七個模糊子集，即NB（負大），NM（負中），NS（負小），ZO（零），PS（正小），PM（正中），PB（正大），如圖3所示。

圖3 隸屬度函數Fig.3 Membership Function

考慮力矩補償系數與機器人關節角度誤差及誤差變化率之間的非線性關系，根據控制經驗建立一套完整的模糊控制規則，如表1所示。

表1 模糊規則庫Tab.1 Fuzzy Rule Base

最后，采用“If—Then”語句進行模糊推理，利用重心法解模糊，獲得關節力矩補償系數u，將其代入式（7），得到關節補償力矩。關節補償力矩與前饋關節力矩共同控制機器人按照規劃關節角度轉動。

4 仿真分析

4.1 仿真模型

在Matlab/Simulink中建立二自由度機器人關節角度追蹤控制模型，其建模參數為具有測量誤差的實測值。控制模型充分考慮機器人的建模誤差和環境干擾。以ADAMS 中建立的模型代替機器人本體，建模參數使用理論值。理論值和實測值，如表2所示。

表2 機器人參數Tab.2 Robot Parameters

設計環境干擾模型，如式（8）：

式中：τq—環境干擾力矩；t—時間；a—Matlad/Simulink 生成的隨機數。

將ADAMS和Matlab/Simulink結合，對所設計控制方法進行仿真。仿真模型，如圖4所示，圖4中的模糊控制，如圖5所示。

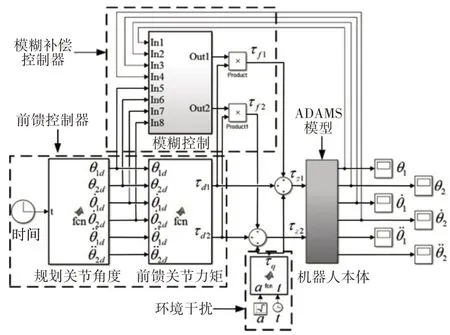
圖4 聯合仿真模型Fig.4 Joint Simulation Model

圖5 模糊控制框圖Fig.5 Block Diagram of Fuzzy Control System

4.2 仿真結果分析

4.2.1 規劃關節角度

規劃關節1在（0～4）s從0 rad運動到1/3 rad，（4～8）s從1/3 rad 返回到0 rad；規劃關節2 在（0～4）s 從0 rad 運動到-2/3 rad，（4～8）s從-2/3 rad返回到0rad。機器人一般做周期性往復運動，為保證轉向的平穩性，要求在0 s、4s和8s時，兩關節的角速度和角加速度均為0。以5次多項式規劃機器人關節角度，關節1和關節2的規劃角度如式（9）、式（10）。所規劃的關節角速度和角加速度由規劃關節角度求導獲得，因此不再一一列出。

4.2.2 仿真結果分析

將規劃關節角度代入仿真模型，得到機器人實際關節角度對規劃關節角度的追蹤曲線以及關節角度追蹤誤差，如圖6實線所示。

采用同樣的規劃關節角度，使用文獻[11]中的前饋和PID結合的控制方法，其關節控制力矩如式（11）所示。

取KP1=2×106；KP2=2×105；KI1=KI2=104；KD1=KD2=104；仿真結果，如圖6虛線所示。

圖6 關節角度追蹤曲線及誤差Fig.6 Tracking Curve and Error of Joint Angle

仿真結果表明，在機器人存在建模誤差和環境干擾的情況下，利用兩種控制方法均能使機器人追蹤規劃關節角度，其中利用前饋和PID結合的控制方法，機器人實際關節角度約0.5s才能收斂到規劃關節角度，穩定后的誤差絕對值大于1×10-3rad。利用所設計控制方法，實際關節角度不存在波動，且其誤差絕對值始終小于1.5×10-4rad，約為前饋和PID結合控制方法最小誤差的七分之一。證明采用前饋控制加模糊補償的控制方法對減小關節角度收斂時間是有效的。

5 結論

提出一種前饋控制加模糊補償的關節角度追蹤控制方法，實現了不確定性機器人關節角度的及時追蹤。采用基于動力學模型的前饋關節力矩減小可能出現的角度追蹤誤差。采用模糊控制計算關節力矩補償系數，進一步獲得關節補償力矩，對角度誤差進行補償。仿真結果表明，該控制方法得到的實際關節角度值無波動，且誤差絕對值小于1.5×10-4rad，具有良好的關節角度追蹤效果。