礦用混凝土噴射機齒輪傳動多目標模糊優化

曹 陽，馬 軍，李曉科，路 迪

（1.鄭州輕工業大學河南省機械裝備智能制造重點實驗室，河南 鄭州 450002；2.河南北工機械制造有限公司，河南 商丘 476000）

1 引言

在機械傳動中，齒輪傳動是最主要、也是應用最廣泛的一類傳動，很多文獻對齒輪傳動優化進行了深入的研究，出于節約資源，降低成本的目的，這些研究多以齒輪傳動的結構優化作為目標[1-4]。然而，現代機械系統是一個與工況環境密切相關的復雜性系統，具有多變量、強耦合及非線性的特點[5]，例如在礦山多粉塵、高溫高濕的惡劣工況下，礦用混凝土噴射機齒輪系統不僅受作業空間的限制，而且要有足夠的安全平穩性，其約束指標中往往存在大量模糊的因素，它們從完全容許到完全不容許是一個不確定的過渡過程，不考慮這些模糊不確定因素的優化方法是不合理的，因此這是一個必須綜合考慮經濟性和平穩性的多目標模糊優化問題。針對齒輪傳動多目標模糊優化，一般的處理方法是通過模糊規劃理論將其轉化為多目標確定性優化問題，然后再進一步應用優化算法來進行求解，例如罰函數法、擬牛頓法、復合形法等，這些算法在理論上具有較好的成熟度，但都屬于局部優化算法，對于齒輪傳動優化問題只能獲得局部最優解。

因此后來研究者更多的是將具備一定全局搜索能力的啟發式算法應用在齒輪傳動優化中，其中，遺傳算法以其不依賴梯度信息，具有全局、并行的優化性能而被廣泛采用[6-10]，但對于齒輪傳動多目標模糊優化設計問題，基本的遺傳算法不僅收斂速度有限，而且還難以保證解的全局最優性，需要結合優化模型的具體特點提出有針對性的優化求解方法。

根據礦用混凝土噴射機齒輪傳動優化設計模型的多目標、模糊性特點，通過降半梯形隸屬度函數和二級模糊評判方法處理模糊性能約束，將多目標模糊優化問題轉換為確定性多目標優化問題，在此基礎上，提出一種改進的混合遺傳算法進行優化求解，并通過與基本遺傳算法優化結果的對比，驗證其有效性和實用價值。

2 礦用混凝土噴射機齒輪傳動多目標模糊優化建模

礦用混凝土噴射機齒輪傳動是一個二級直齒圓柱齒輪傳動。從減輕質量、節省材料和降低成本的經濟性指標考慮，要求該傳動系統結構緊湊，這就要求齒輪傳動的徑向和軸向尺寸要最小，即兩齒輪中心距和齒輪分度圓柱體體積最小。同時在齒輪傳動過程中經常要正反轉，因此盡量小的轉動慣量可有效保障傳動平穩性。基于上述考慮，礦用混凝土噴射機齒輪傳動的優化目標如下：

其中兩齒輪中心距：

齒輪分度圓柱體體積：

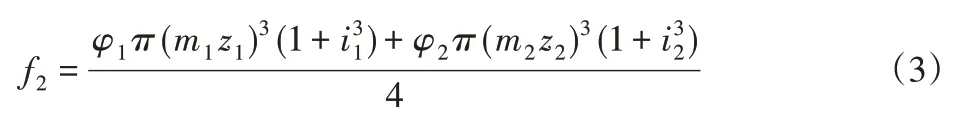
結合文獻[10]，傳動系統轉動慣量：

其中：

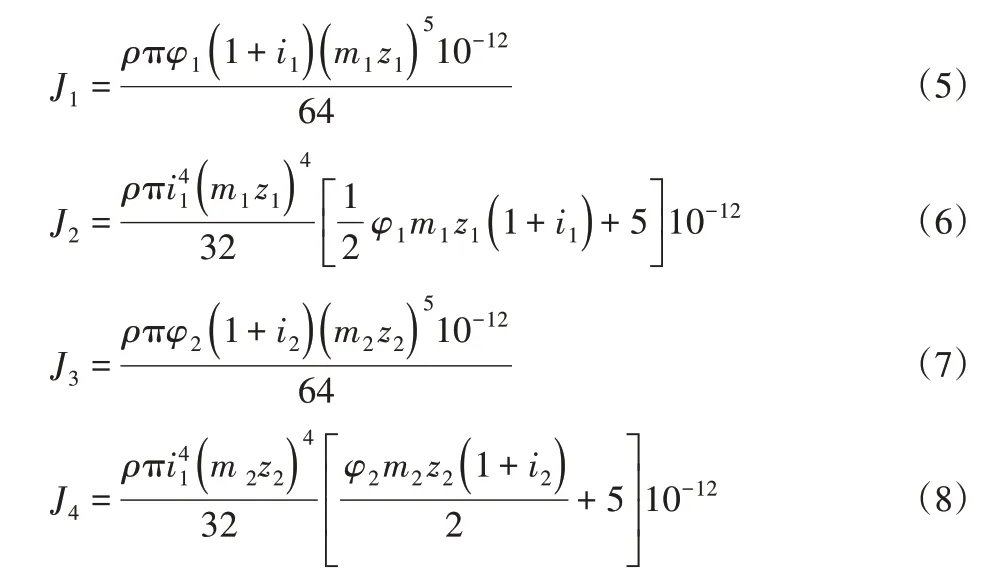
式中：J1、J2、J3、J4—四個齒輪的轉動慣量；m1、m2—一、二級齒輪法面模數；i1、i2—一、二級傳動比；z1、z2—一、二級的小齒輪齒數；φ1、φ2—一、二級小齒輪的齒寬系數。

考慮到傳動系統的平穩性和空間布局，約束條件包含幾何約束與性能約束。幾何約束包括齒數、模數、傳動比和齒寬系數約束。

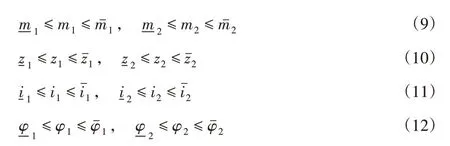
性能約束包括齒面接觸與齒根彎曲疲勞強度約束。礦用混凝土噴射機齒輪傳動多目標優化中，準確的齒面接觸疲勞許用應力和齒根彎曲疲勞強度很難獲得，一般都是模糊的，處于完全許用到完全不許用的中間過程。

①一、二級齒輪齒面接觸疲勞強度約束

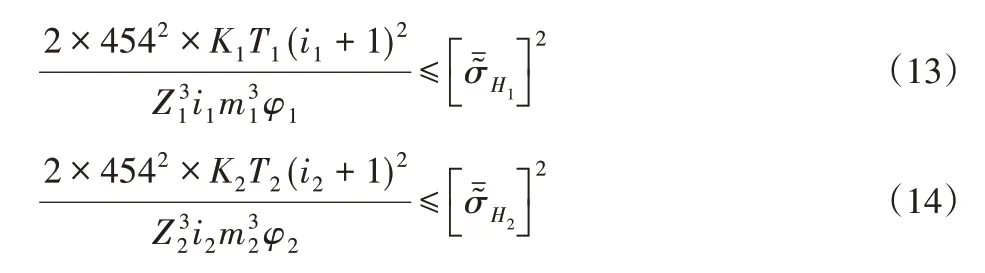
②一、二級齒輪齒根彎曲疲勞強度約束

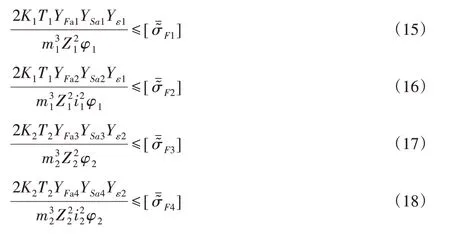
式中：K—載荷系數；T—傳遞的扭矩；YF—齒形系數；YS—齒根應力修正系數；Yε—重和度系數。因性能約束要考慮約束的模糊性，式中：[σˉ?H]—模糊許用接觸應力；[σˉ?F]—模糊許用彎曲應力。以上約束條件中引用的符號“～”表示具有模糊性，引用的符號“ˉ”或“_”表示參數的上或下界。

不失一般性，礦用混凝土噴射機齒輪傳動多目標模糊優化模型可以統一表示為求：

3 礦用混凝土噴射機齒輪傳動性能約束的模糊性處理

3.1 模糊性能約束的隸屬度函數

對于礦用混凝土噴射機齒輪傳動多目標模糊優化問題，引入模糊理論來處理性能約束中的模糊性問題，即把齒面接觸疲勞許用應力和齒根彎曲疲勞強度約束都處理為一個隸屬度函數，從而實現模糊多目標優化模型到確定性多目標優化模型的轉化，其原模型約束條件仍嚴格成立，從而在保證科學性的同時，很好地兼顧了礦用混凝土噴射機齒輪傳動設計的經濟性和平穩性兩個目標。隸屬度函數一般要根據問題的模糊性質來具體確定，考慮到齒面接觸疲勞許用應力和齒根彎曲疲勞強度的模糊性具有一定的相似性，因此統一采用降半梯形分布的隸屬度函數。齒面接觸疲勞許用應力和齒根彎曲疲勞強度的隸屬度函數uσ(x)，如圖1所示。

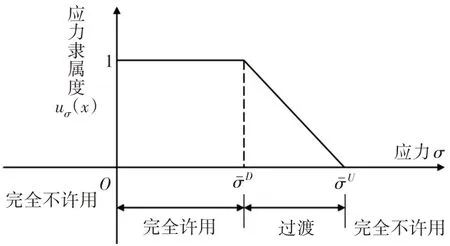
圖1 降半梯形分布隸屬度函數uσ(x)Fig.1 The Semi-trapezoidal Membership Function uσ(x)

模糊性能約束的隸屬度函數表達為：

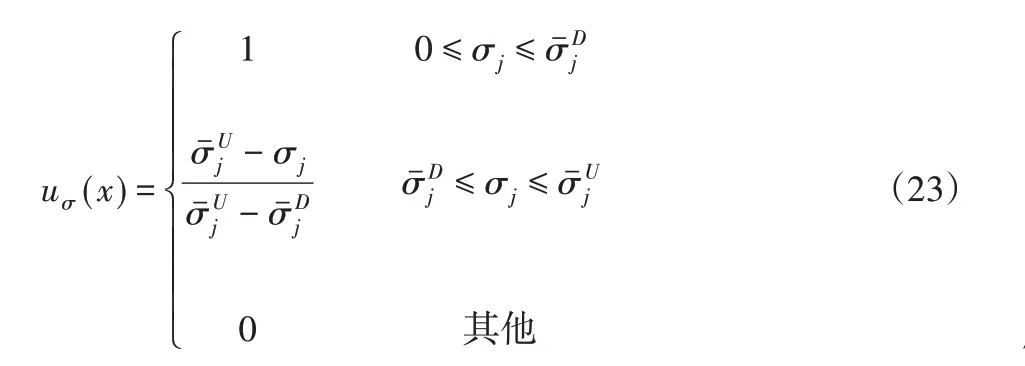
基于模糊數學分解定律，以一系列水平值截取模糊隸屬度函數uσ(x)，可獲得不同設防水平下的水平截集λ，即在上式中設：

從上式可得到：

因此，許用應力由水平截集λ的值決定。水平截集λ值越大系統越安全平穩，越小系統越經濟。為了使系統即平穩又經濟，應尋找一個最優水平值λ*。

3.2 最優化水平截集的模糊綜合評價

最優水平值λ*可以采用兩級模糊綜合評判法來確定。所謂兩級模糊綜合評價，首先對單個因素進行評判，再對所有因素進行綜合評判。

3.2.1 根據設計要求確定影響因素集及每個因素的等級

式中：Sk—第k個影響因素，k=1，2，…，m。因素等級可以表達為sk={sk1，sk2，…，skp}。其中，skl—第k個影響因素的第l個等級。l=1，2，…，p。

3.2.2 根據評判對象的取值范圍確定備擇集

由于評判對象必然包含在一個區間內，為了通過確定該評判對象的準確值，可以將區間離散化后得到備擇集。

式中：Vj—第j個備擇集評判子對象，j=1，2，…，n

3.2.3 建立一級模糊評判矩陣

對每一個影響因素進行評判，以確定影響因素對備擇集評判子對象的隸屬度。設備擇集V中第j個評判子對象Vj按因素集S中第k個影響因素Sk評判，Sk對評判子對象Vj的隸屬度為γkj，則評判結果可以用評判集合Rk表示，Rk是備擇集上的一個模糊子集，則單因素評判集合可表達為：

同理對每個影響因素進行評判，獲得單因素隸屬度集合，構成因素集的一級模糊評價矩陣：

3.2.4 建立因素權重集

在模糊多目標優化問題中，決策者的評價不僅具有不確定性，還往往具有一定的主觀性，各評價因素的重要程度一般是不同的，不可以等同對待。為了反映各個評價因素的差異性，決策者可以對分目標的評價因素進行賦權，即對各個評價指標設置不同的重要度。為反映各個因素的重要程度，對各因素賦予相應權重，權重集為：

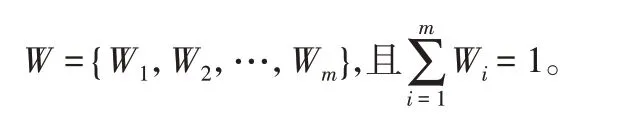
3.2.5 模糊綜合評判

綜合考慮所有因素對評判對象的影響，獲得模糊綜合評判集為：

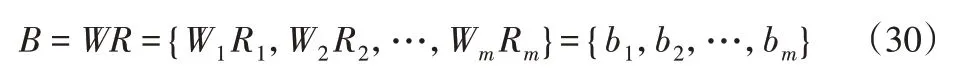
式中：bi—模糊綜合評判指標。

最后，用加權平均法得最優水平截集為：

這樣就可以將模糊多目標優化問題轉化為最優水平截集上的確定性多目標優化問題：

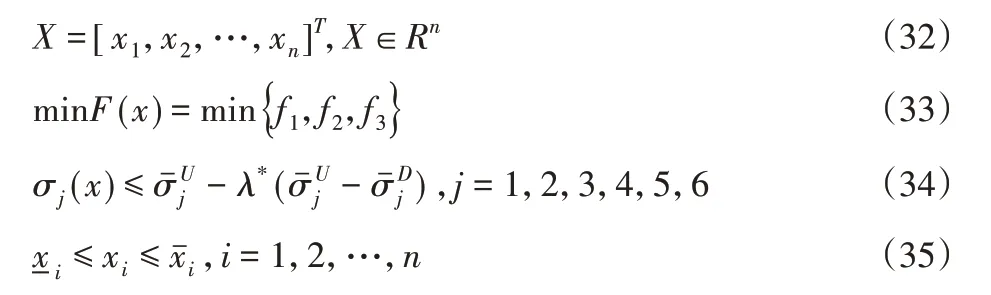
4 面向礦用混凝土噴射機齒輪傳動多目標優化求解的混合遺傳算法

對有一定復雜約束的優化問題求解，基本遺傳算法面臨難以快速進入可行域以及難以找到全局最優解的問題。為了在擴大解空間的同時提高求解搜索效率，在基本遺傳算法基礎上融入局部搜索過程，提出了改進的混合遺傳算法，即在混合遺傳算法中，將每一代種群中的個體排列順序打亂，亂序之后種群中的所有個體就都有可能被選中。通過變量迭代和亂序操作方法，（1）增加了種群中所有個體適應度，（2）可以使所有個體被選擇的概率均等。該算法步驟，如圖2所示。

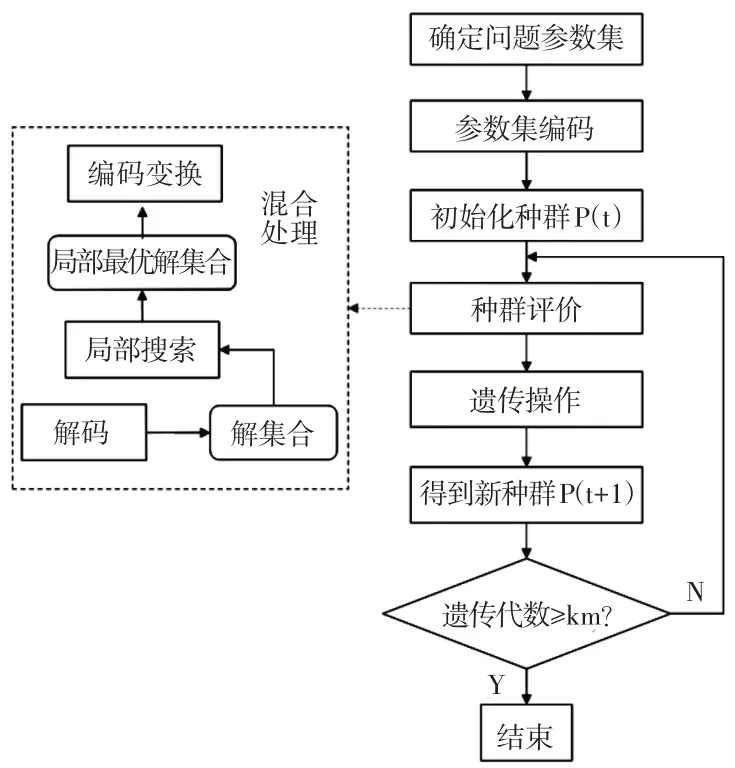
圖2 混合遺傳算法流程Fig.2 The Flow Diagram of Hybrid Genetic Algorithm

（2）對種群所有個體進行編碼，采用二進制編碼的方法。

（3）在變量設定的范圍內隨機產生第一代種群，該種群中的第一個個體為x0。

（4）對種群中各個體進行適應度評價。首先對種群各個體進行解碼（采用二進制解碼），并求出當前種群中目標函數最小值min(f(x)) 及其對應的個體xb，并將它們保留。令fmin=min(f(x))，xmin=xb；最后對該種群中的各個體適應度函數值進行評價，fs(x)=max(f(x))-f(x)，若max(fs(x)≤κ，則計算結束，否則執行（5）。

（5）按照式（1）進行變量迭代操作，生成新一代種群。

（6）亂序和交叉操作。亂序操作可以通過調用randperm（）函數來完成；采用單點交叉的方式進行交叉操作，即交換兩個染色體上隨機選定基因位置上的單個基因片段。依照給定的交叉概率pc進行交叉操作。若是多維變量，則基因片段交換的位置是相互獨立并且隨機的。

（7）按照預先設定的變異概率pb進行變異操作。同交叉操作類似，變異操作也采用隨機單點變異，即隨機選中個體，再對個體中某一位基因的0、1做更改。若是多維變量，則個體各分量基因變異是獨立和隨機進行的。

（8）重復（1）到（8），計算達到最大遺傳代數km時停止計算，最終輸出最優解。

上述步驟中，關鍵的選擇操作按下式進行。

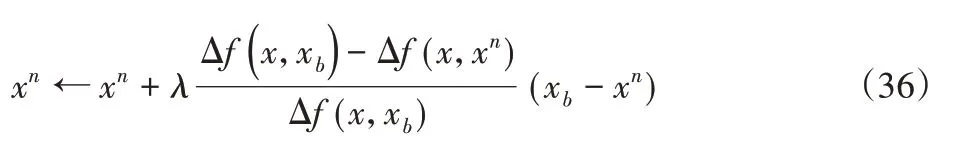
式中：λ—學習因子；xb—目標函數最小（或最大）的染色體。對最小值問題，其適應度值反而越大，以比例選擇的角度來說，目標函數值越小，個體就越容易被選中。Δf(x，xb)—最大目標函數差值，且：

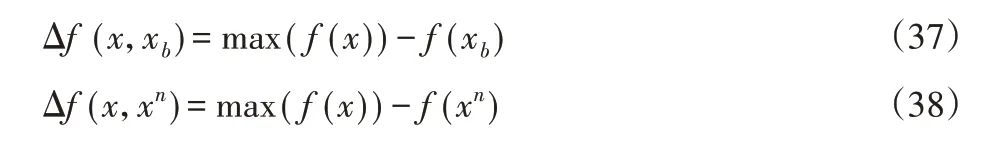
5 實例分析

5.1 模糊性處理

某礦用混凝土噴射機齒輪傳動系統在一定強度和剛度條件下，要求傳動系統結構緊湊，總體積小，轉動慣量小。傳動系統主傳動功率為5.5kW，輸入軸轉速960r/min。總傳動比i=25。按非對稱分布，高速級與低速級的齒寬系數分別為φ1=0.8、φ2=0.8。一級小齒輪45鋼調質處理，大齒輪45鋼正火處理；二級大、小齒輪都為45鋼表面淬火處理。

齒輪傳動中兩齒輪中心距、齒輪分度圓柱體體積和傳動系統轉動慣量，受到齒輪的齒數、模數、齒寬、傳動比等參數的影響。增加齒數m、模數z和傳動比i都可以提高兩齒輪中心距，而齒寬增加會增大體積，因此優化設計變量為：

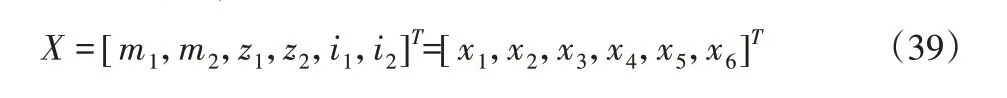
水平截集λ的取值按兩級模糊綜合評判確定。影響因素及其等級，如表1所示。

表1 因素集與因素等級Tab.1 The Factor Set and Its Grade

由于水平截集λ的取值區間為［0，1］，按步長0.1將其離散后得到備擇集V=｛0，0.1，0.2，0.3，0.4，0.5，0.6，0.7，0.8，0.9，1.0｝。因素權重集為W=｛0.25，0.25，0.15，0.15，0.10，0.10｝。

經過一級和二級模糊綜合評判，得到兩級模糊綜合評判集為：B=｛0，0.061，0.186，0.470，0.560，0.593，0.525，0.403，0.261，0.131，0.040｝。按加權平均求得最優水平值：

將最優水平值λ*代入各模糊性能約束的隸屬函數中，獲得各性能約束的取值范圍，這樣將多目標模糊優化問題轉化為常規多目標優化問題。

5.2 優化求解

使用混合遺傳算法對優化模型進行求解，設種群數量Np=20，二進制編碼長度Nb=［8，8，8，8，8，8］，交叉概率pc=0.7，變異概率pb=0.1，最大遺傳代數為100，求解后的結果采用合成權重的比較選取一組解，經圓整后為x1=3，x2=3，x3=20，x4=20，x5=4.3，x6=3.7。在種群進化過程中，各個體均向著最優適應度方向進化，直到達到最優適應度。如圖3（b）分析可知，隨著算法迭代次數的增加雖然最佳適應度均值會有起伏波動，但從全局趨勢來看最佳與平均適應的平均值都在穩步下降。

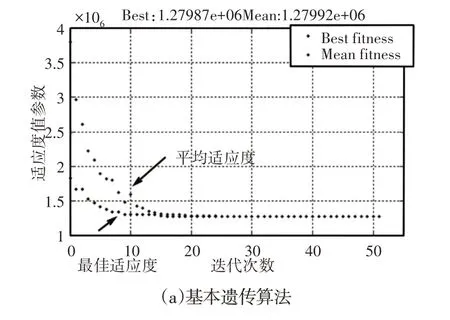
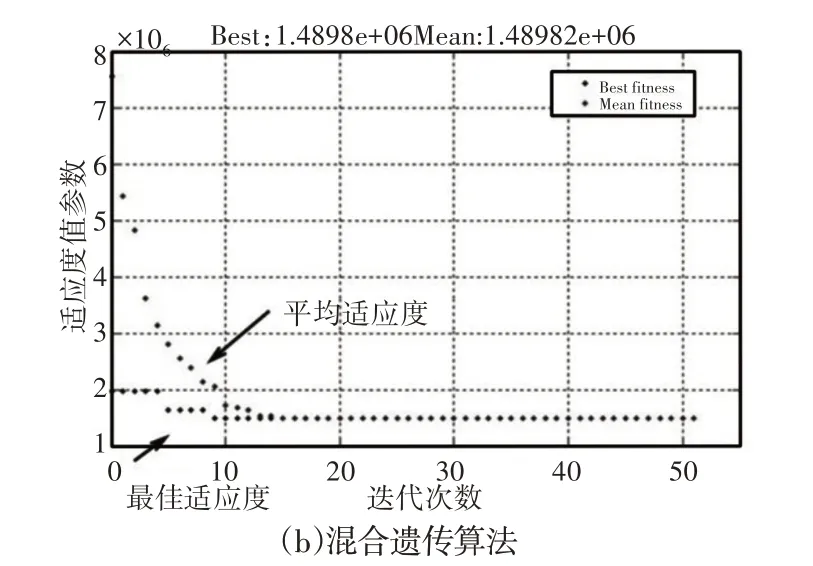
圖3 種群中個體平均適應度Fig.3 Average Fitness Values of the Population Individuals

這表明算法的穩定性較好同時可以看出算法的后期收斂速度較慢。對比圖3（a）的基本遺傳算法，可以看出混合遺傳算法的收斂速度要略大一些。

在種群進化過程中，各個體均向著最優適應度方向進化，如圖4所示。遺傳過程中各局部最優值所對應的個體數量，對比圖4（a）、圖4（b）可知，混合遺傳算法中最優適應度值區間中個體數量也要高于基本遺傳算法。

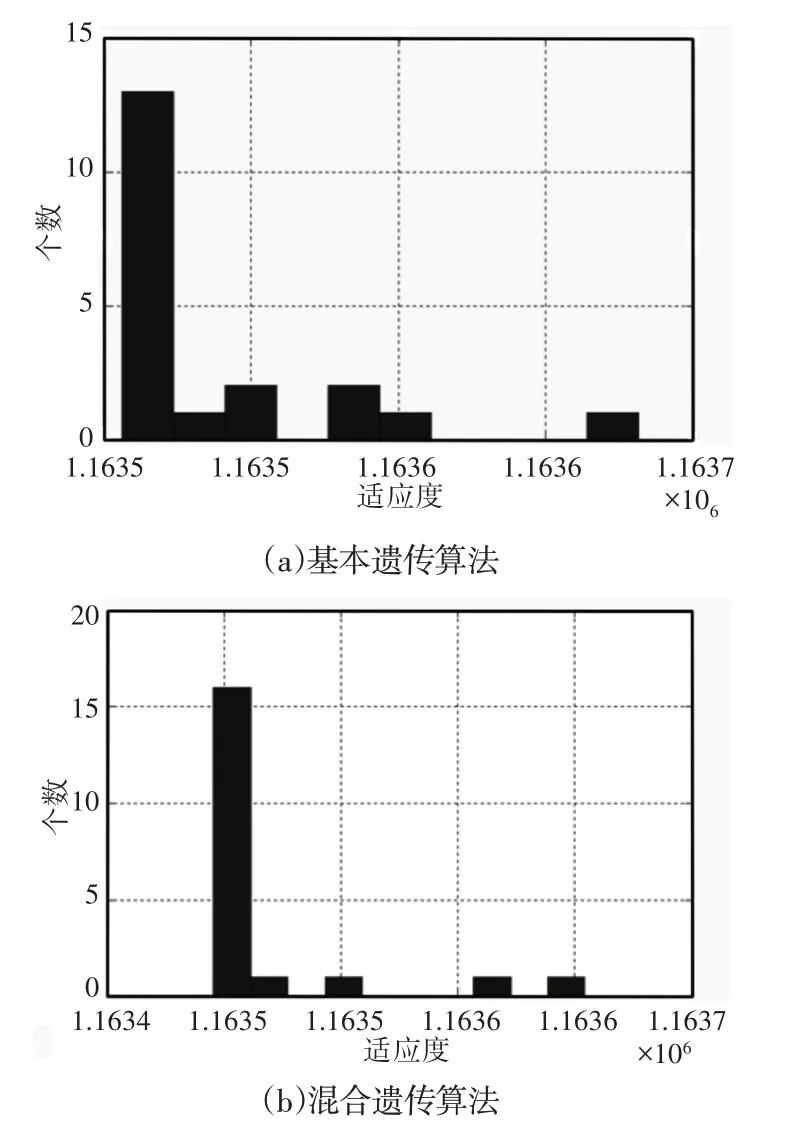
圖4 各局部最優適應度對應種群個數Fig.4 The Population Size According to the Local Optimal Fitness Degree

將結果與遺傳算法得出的結果，如表2所示。從優化的結果可以看出，采用的混合遺傳算法，其中心距減少16%，齒輪總體積減少32%，轉動慣量減少27%，優化效果較顯著。

表2 優化結果對比Tab.2 The Comparison of the Optimization Results

6 總結

（1）采用降半梯形分布模糊隸屬度函數和兩級模糊評判法，可以有效的將礦用混凝土噴射機減速器齒輪傳動設計模糊優化模型轉化為確定性優化模型。

（2）在優化模型的求解方面，對比基本遺傳算法，改進后的混合遺傳算法穩定性較好，收斂速度更快，而且更接近全局最優解。

（3）采用混合遺傳算法，優化后的礦用混凝土噴射系統其中心距減少16%，齒輪總體積減少32%，轉動慣量減少27%，結構更緊湊，經濟性和平穩性更優。