A/D采樣方式測量瞬時轉速的誤差影響因素分析

劉 永，李 捷，龔立雄

（1.湖北汽車工業學院機械工程學院，湖北 十堰 442002；2.湖北工業大學機械工程學院，湖北 武漢 430068）

1 引言

瞬時轉速測量從測量硬件的角度可以分為A/D采樣和高頻定時器或時鐘脈沖計數兩種方式，其實質都是對電容、電渦流、光電碼盤、磁電式等轉速傳感器發出的單個周期方波脈沖的頻率或時間進行測量，從而得到瞬時轉速值[1]。

兩種方式各有特點，高頻定時器或時鐘脈沖計數方式需要設計硬件電路、數據量少、擴展性差，而A/D采樣方式無需設計硬件電路、擴展性好、數據量大，在高轉速時為了達到一定的測量精度對采集板卡的最高采樣頻率有要求。利用壓電晶片輸出電壓和轉速的關系，可以測量轉軸的轉速，為開發新型的轉速傳感器拓展了方向[2]。以磁電式轉速傳感器、測速齒輪、采集板卡、工控機為硬件構成的測速系統，采用A/D采樣方式測量瞬時轉速，其測量誤差主要有測速齒輪的齒形誤差、采樣頻率誤差、單個周期方波的采樣點計數誤差構成[3]。齒形誤差主要包括齒輪的加工和安裝誤差，文獻[4]從理論上分析了齒輪輪齒加工分布不均、安裝偏心等引入的測量誤差。

文獻[5-7]通過仿真分析了齒輪安裝偏心、轉軸扭振、傳感器支架振動引入的測量誤差，分析結果表明上述引入誤差分為齒輪邊緣切線和徑向兩個方向。切線方向相當于對傳感器波形加入調頻信號，對測速精度影響較大；而徑向方向相當于對傳感器波形加入調幅信號，對測速精度沒有影響。采樣頻率誤差主要由采集卡的觸發誤差和高頻晶振的頻率誤差構成，目前采集卡的性能較高，此類誤差較小。單個周期方波的采樣點計數誤差是由于采樣時間與傳感器波形周期時間不匹配引起的，通過仿真、理論分析采用自適應采樣法[8]、插值法[9]可以減小此類誤差，但這些方法不易實施。為了定量分析采用A/D采樣軟件計數方式測量瞬時轉速引入誤差的原因、提高測量精度，本文通過理論分析了計數誤差的成因，并推導了軟件計數誤差公式，通過實驗驗證了采樣頻率、轉速對誤差的影響規律，為實驗條件下選擇合適的采樣頻率與測速范圍、降低采樣點計數誤差提供參考。

2 測速方法

采用的轉速傳感器為磁電式，傳感器內部有信號處理電路將測速齒輪經過時產生的原始類正弦信號濾波、整形、放大為幅值為5V的方波脈沖信號。轉速傳感器方波采樣時的示意圖，如圖1所示。

圖1 轉速傳感器方波采樣點示意圖Fig.1 The Sampling Point Diagram on the Square Wave of Speed Sensor

瞬時轉速可表示為：

式中：fc—數據采集卡設置的采樣頻率；Z—鋼制測速齒輪的齒數；

N—一個周期信號的采樣點的個數。

從式（1）中可以看出，采樣頻率fc和齒數Z為常量，因此只要測出圖1中一個信號周期的采樣點個數，即可獲得瞬時轉速值。設計的測速算法為軟件計數法。先設置閾值判斷高、低電壓，再對圖1中的高、低電壓分別進行采樣點計數，計數數值為N1、N2，對N1、N2求和，從而獲得一個周期信號的采樣點個數N，代入式（1）后即可測得瞬時轉速。由式（1）可得：

式中：f—方波信號的瞬時頻率，測速齒輪的齒數為z=30，由式（1）、式（2）可得：

由式（3）可知瞬時轉速的大小與方波信號的瞬時頻率成正比關系。采集的一段傳感器輸出信號及采用上述方法轉速測量值，此時設置的采樣頻率為50kHz，如圖2 所示。從圖2 可以看出，在時間段（1.2～1.25）s，對應的測量轉速在487r/min左右，在時間段（1.35～1.40）s，對應的測量轉速在537r/min左右，前一時間段對應的周期方波信號的頻率明顯小于后一時間段。此現象證明了周期方波信號的瞬時頻率和瞬時轉速值成正比關系。

圖2 傳感器輸出信號及轉速測量值Fig.2 The Signal of Sensor Output and the Value of Speed Measurement

3 測量誤差分析

3.1 測量誤差理論分析

將式（1）按泰勒公式一階展開，可得：

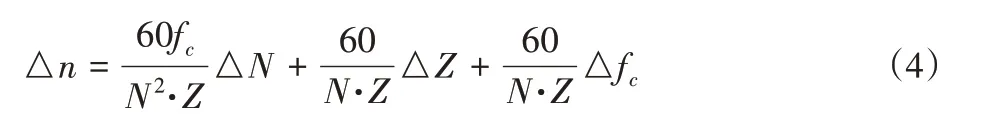
式中：△n—轉速測量絕對誤差；△N—采樣點計數誤差；△Z—齒形及測速齒輪安裝誤差；△fc—采集誤差，只分析第一種誤差，即A/D采樣軟件計數方式引入的測量誤差，故有

由式（1）、式（5）可得：

式中：ε—轉速相對誤差。

采集的一個周期的轉速信號與采樣重構波形示意圖，如圖3所示。

圖3 轉速原始信號與采樣重構波形示意圖Fig.3 The Diagram of the Original Signal and Sampling Refactoring Waveform on Rotational Speed

從圖3可以看出，轉速原始波形的周期為t，采樣重構波形周期為t1，兩者時間不相等，這是測量過程引入誤差的原因。由于機械摩擦等原因，即使在平穩轉速狀態，轉速也會有小的波動，因此在不同時刻信號高電壓、低電壓經歷的時間并不相同。采樣點為等時間間隔，若消除此誤差需保證原始波形和采樣重構波形在高、低電壓跳變的時刻保持同步，顯然這不容易做到。在對重構擬合波形采樣點計數計算單個波形周期時間時，會出現多計或少計一個的情況。因此，可取△N= 1，實驗裝置中測速齒輪的齒數為Z=30，由式（1）、式（6）可得：

式中：n—瞬時轉速。在轉速平穩狀態用式（7）評定誤差時可用對應時間段的平均轉速近似替代。由式（7）可以看出，測量誤差ε與采樣頻率fc成反比關系，與瞬時轉速n成正比關系。

3.2 測量誤差實驗分析

圖測量瞬時轉速實驗裝置測控原理圖，如圖4所示。實驗裝置為變轉速液壓系統，動力源為伺服電機13加齒輪泵14，測速齒輪4裝在液壓馬達3的軸上，正對著安裝在支架上的磁電式轉速傳感器8。

圖4 實驗裝置原理圖Fig.4 The Principle Diagram of the Experimental Apparatus

編制的測控程序為電機轉速開環控制，通過在界面上給定電機轉速，電機帶動齒輪泵旋轉，油液在液壓系統中流動帶動液壓馬達旋轉，從而可以測量液壓馬達的瞬時轉速。通過Lab-VIEW[10]測控程序將磁電式轉速傳感器8發出的方波原始信號采集下來，再在Matalab軟件中根據式（1）編寫測量程序即可得到瞬時轉速曲線圖及測量誤差的計算值。程序界面上顯示的轉速為LabVIEW中提取單頻子vi測得的一定時間段的平均轉速。

3.2.1 相同轉速不同采樣頻率

不同采樣頻率液壓馬達穩態轉速約為332r/min時的測量曲線圖，如圖5所示。對應的測量誤差，如表1所示。從圖5（a）可以看出，采樣頻率設置為3kHz時測量的轉速為鋸齒狀毛刺，測量方法引入的誤差較大掩蓋了轉速的真實波動，從表1可以看出測量相對誤差為5.54%，測量精度較低；采樣頻率設置為7kHz時測量的轉速同樣為鋸齒狀毛刺，幅值相對于圖5（a）降低一半。

圖5 不同采樣頻率液壓馬達穩態轉速約為332r/min時的曲線圖Fig.5 The Steady State Rotational Speed Curve of Hydraulic Motor with Different Sampling Frequencyat the Speed of 332r/min

表1 相同轉速、不同采樣頻率下的測量誤差Tab.1 The Measuring Error under Same Speed and Different Sampling Frequency

從表1 可以看出測量相對誤差為2.37%；采樣頻率設置為12kHz時測量的轉速波動鋸齒狀毛刺形狀相比前兩種情況已顯著減小，已經可以看出轉速波動成分。從表1可以看出測量相對誤差為1.38%；采樣頻率設置為110kHz時測量的轉速波動鋸齒狀毛刺已經消失，轉速波動成分十分明顯，從表1可以看出測量相對誤差為0.15%，引入的測量方法誤差已經很小，測量精度較高。從表1還可以看出四次測量的穩態平均轉速均約為332r/min，采樣頻率分別設置為3kHz、7kHz、12kHz、110kHz時，對應的測量誤差分別為5.54%、2.37%、1.38%、0.15%。在相同的轉速下，隨著采樣頻率的增大，測量誤差也隨之減小。從數值大小比看，在相同的轉速條件下，測量誤差與采樣頻率符合式（7）中的反比關系。

3.2.2 相同采樣頻率不同轉速

設置相同采樣頻率50kHz、不同的轉速條件下的誤差實驗數據，如表2所示。由于轉速不同，實際測量的轉速波形的波動成分沒有可比性，故沒有作出對應的轉速曲線圖。從表2可以看出在穩態平均轉速分別為146.67r/min、467.5r/min、788.41r/min、1055.9r/min 時，對應的測量誤差分別0.15%、0.47%、0.79%、1.06%。在相同的采樣頻率下，隨著轉速的增大，測量誤差也隨之增大。從數值大小比看，在相同的采樣頻率條件下，測量誤差與轉速符合式（7）中的正比關系。上述實驗結果驗證了采樣點計數法引入的測量誤差式（7）的正確性。

表2 不同轉速、相同采樣頻率下的測量誤差Tab.2 The Measuring Error Under Same Sampling Frequency and Different Speed

4 結論

通過理論和實驗分析了采用A/D采樣方式的軟件計數法測量瞬時轉速時引入誤差的原因及影響誤差大小的因素。研究證明了提高采樣頻率、降低轉速可以顯著地降低引入的測量誤差。由于引入的測量誤差與采樣頻率成反比關系，與轉速成正比關系，因此要在合理的轉速和測量精度范圍內選擇合適的采樣頻率。過高的采樣頻率并不會讓測量誤差無限制降低，反而會增加硬件成本和數據采集量，影響測量系統運行速度。