航空發動機在翼清洗時機Wiener預測模型研究

閆 鋒，姚星宇

（中國民用航空飛行學院航空工程學院，四川 廣漢 618307）

1 引言

航空發動機使用過程中難免出現發動機內涵氣路部件積污的情況，發動機性能和經濟性將會變差，航空公司通常采用發動機在翼清洗的方法來改善發動機的性能。

廠家的清洗工作建議是以固定時間間隔（如1000飛行小時）給定的，這種方式的優點是工程管理簡單，維修時間易于控制，其缺點在于發動機的清洗效能沒有充分評估，可能會出現發動機性能狀態良好，不需要開展清洗工作，而頻繁實施清洗，導致維護過剩造成浪費。也可能會出現發動機在固定清洗節點前，性能已經衰退至臨界值，需要提前開展清洗工作，導致航班計劃以及維修保障計劃改變[1-4]。

利用發動機性能參數（EGTM），基于節省燃油量成本、延長發動機在翼時間而節省的大修成本及清洗成本三者總和最小，得到發動機清洗參數門閥值，通過Wiener 退化模型模擬發動機EGTM在翼衰退規律，進而預測最佳清洗時機，最終實現由傳統固定清洗時間間隔到柔性時間清洗間隔轉變。

2 發動機清洗門閥值確定

2.1 發動機EGTM衰退模型

某航空公司某臺發動機時間與對應的清洗EGTM 值數據，如表1所示。

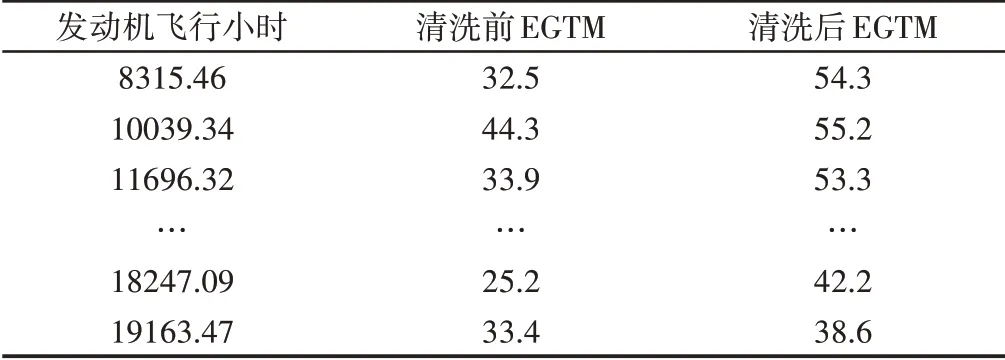
表1 航空發動機清洗數據Tab.1 Aero-Engine Cleaning Data

利用回歸分析得EGTM 衰退模型：

式中：yi—EGTM；xi—在翼時間，可取為飛行小時數；k1，k2—回歸系數，是隨機變量，與樣本有關；k1—衰退率；ε（x）i—隨機干擾項。經過數據處理后可以得到EGTM與飛行小時數的關系為：y=-1.83x+55.2。

2.2 改變門閥值后延長在翼時間與節省大修成本計算

簡化發動機衰退模型如下：

假設1：清洗前后EGTM衰退率不變。

當發動機清洗的門閥值改變后相應的發動機的在翼時間也會隨之改變，由此可以通過改變發動機清洗門閥值的新清洗方式來延長發動機在翼時間從而節省發動機大修成本。

假設2：改變門閥值的量為ΔEGTM，基于假設1可以得到改變發動機清洗門閥值后與原始數據的對比圖，如圖1所示。

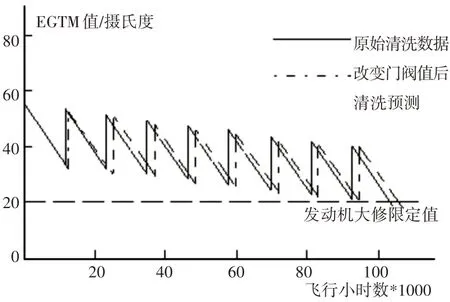
圖1 改變閥值對比圖Fig.1 Comparison Chart for Changing Threshold

發動機大修時間間隔約為20000飛行小時，大修成本約為發動機新機價格的三分之一。

當延長發動機清洗門閥值后由對比圖及數據公式可見延長了發動機的在翼時間為( ΔEGTM/K )*2，式中：K—發動機EGTM衰退率，K=1.83。則通過延長清洗門閥值后節省發動機大修成本為( ΔEGTM/1.91 )*136000美元。

2.3 節省燃油量計算

2.3.1 節省燃油量計算模型

參考文獻[5]給出了節省燃油量計算方式及發動機清洗前后DFF與飛行循環間函數關系，如圖2所示。

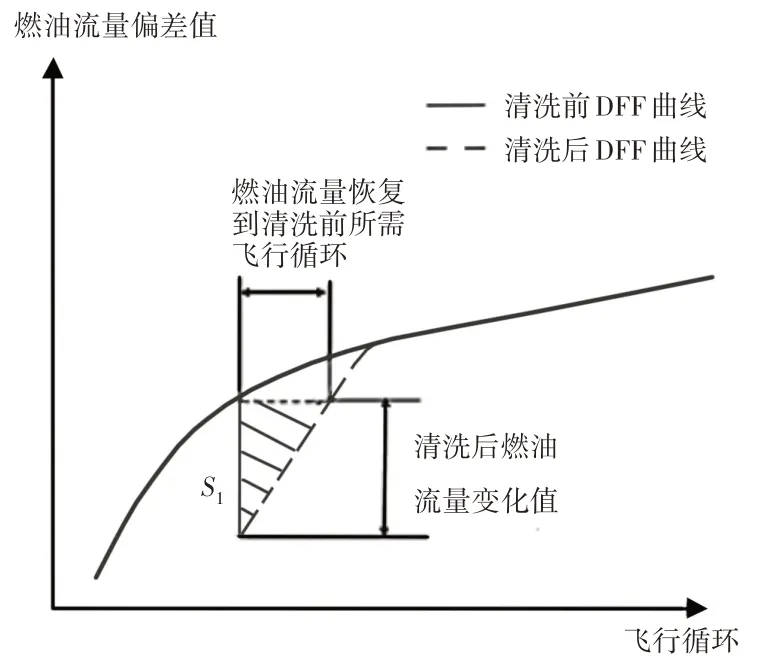
圖2 節油模型圖Fig.2 Fuel-Saving Model Diagram

圖2參數注釋及單臺發動機節省燃油具體算法公式如下：

發動機清洗后巡航消耗燃油偏差量量增量=30臺發動機清洗前燃油偏差量平均值-30臺發動機清洗后燃油流量偏差值平均值。

燃油偏差量恢復清洗前飛行循環間隔由起飛時EGTM變化所對應的飛行循環間隔來計算，依據如下：

（a）燃油流量偏差值測量時更分散；

（b）EGTM值測量更加準確；

（c）發動機性能變化在起飛時能夠更好體現。

單臺發動機節省燃油量公式可表示為：

一次飛行循環節油量=總面積*發動機一次巡航燃油消耗量

其中，總面積=1.2*S1

鑒于某型航空發動機相較于羅羅公司的發動機性能衰退率更低一些，故總面積約為1.1倍的S1。

2.3.2 單臺發動機節省燃油量計算實例

由已知數據可知發動機清洗后燃油流量偏差變化量為0.43，且EGTM恢復至清洗前飛行循環的時間間隔為34700h。由此可知S1=34700*0.43=14921，總面積為17905.2，且發動機單次平均每小時耗油2.7噸約964美元。綜上數據可知單臺發動機清洗后節省燃油流量的成本為1726萬美元。

2.4 基于總成本最低的發動機清洗門閥值確定

發動機的總成本是需綜合考慮發動機大修成本、發動機燃油消耗成本及發動機清洗成本三個因素，發動機總成本為上述三者之和。

改變發動機清洗門閥值后的節約發動機燃油量情況不變，發動機清洗成本為6000美元左右。發動機清洗門閥值的改變主要影響發動機大修成本（在翼時間改變）。改變清洗門閥值后節約的發動機大修成本隨ΔEGTM的增大而增大，發動機總成本相應的隨節省的發動機成本增大而減小，即當發動機大修成本節省值最大時發動機總成本最低。發動Q機的EGTM大修限定值為20℃，為保證發動機安全性則保證發動機的EGTM值衰退到19℃前應得到及時清洗，且保證清洗次數和圖中曲線一直，所以基于發動機節約成本最低情況下ΔEGTM值應為0.6℃。

綜上所述首次發動機清洗門閥值確定在33.6℃。

3 發動機在翼清洗時間預測wiener模型

發動機EGTM性能衰退的Wiener模型如下［6］：

式中：μ—漂移參數；σ—擴散系數；W0(t)—標準Wiener過程其中各參數為E[W(t)]D[W(t)]=σ2t。

3.1 模型參數估計

發動機性能退化的似然函數[7]：

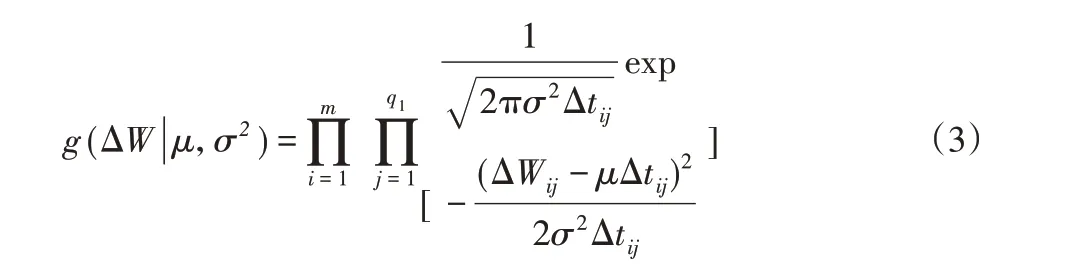
對上式μ和σ分別求偏導可得：

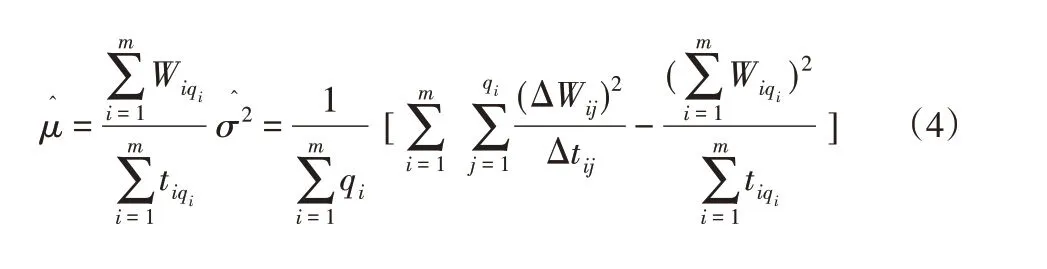
3.2 貝葉斯參數更新

參數更新方程如下：

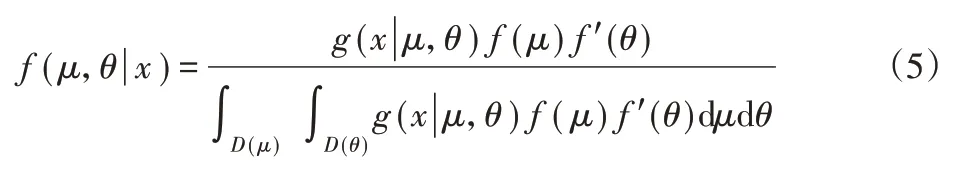
式中：f(μ)，f′(θ)—μ和θ先驗概率密度函數；f(μ，θ|x)—后概率密度函數；D(μ)，D(θ)—μ和θ取值范圍；g(x|μ，θ)—似然函數。設σ2=1/θ2通常檢測的間隔相同，即Δtij=Δt，xij=ΔWij/Δt，則似然函數可以寫成：

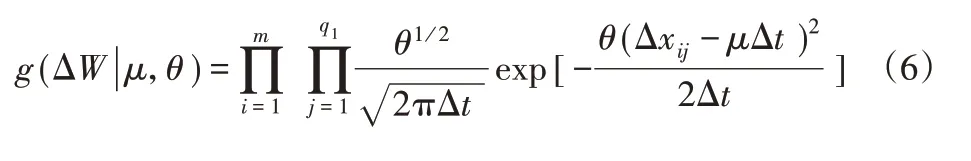
4 清洗時間的預測模型

發動機剩余清洗時間T是退化量W(t)首次達到清洗閾值的時間，可以表示成：

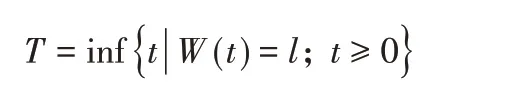
根據文獻T服從逆高斯分布IG(l/μ，l2/σ2)，T的分布函數和概率密度函數分別為：

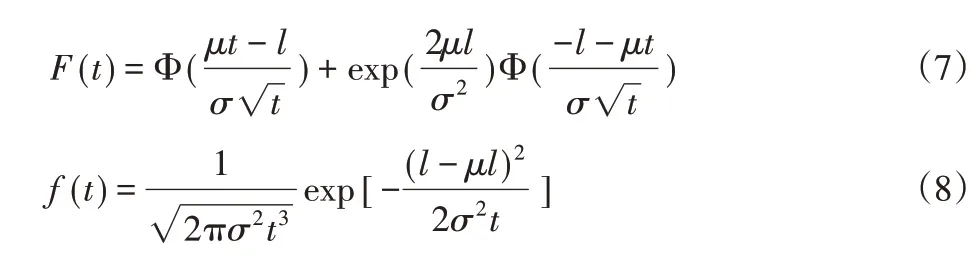
通過Wiener過程參數更新，得到μ和σ2估計的更新值和，其中σ2=1/θ2，t時刻的發動機性能水平：

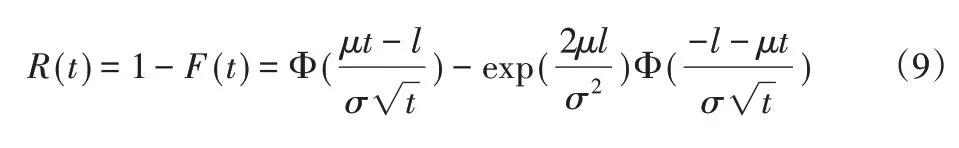
5 仿真實例

5.1 仿真計算

選取某航空公司發動機的EGTM數據，如表2所示。

表2 發動機飛行小時對應的EGTM數據Tab.2 EGTM Data for Engine Flight Hours

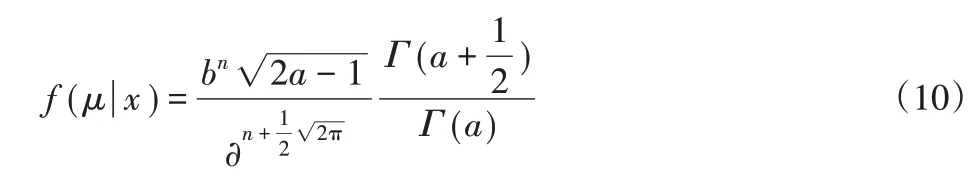
可求得參數估計值，如表3所示。

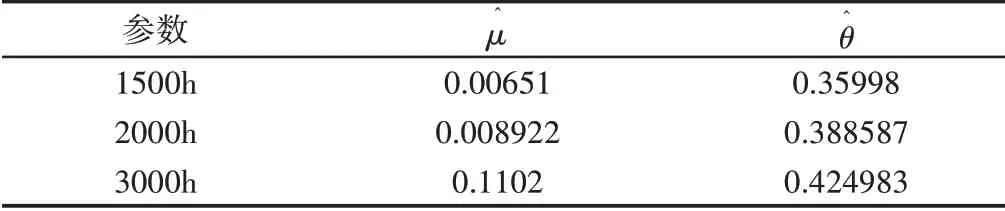
表3 參數估計Tab.3 Parameter Estimation

圖3中f1、f2和f3分別表示發動機在1500飛行小時、2000飛行小時和3000飛行小時時預測的剩余清洗時間分布。根據固定參數法可得發動機剩余清洗時間概率密度函數曲線，如圖3所示。

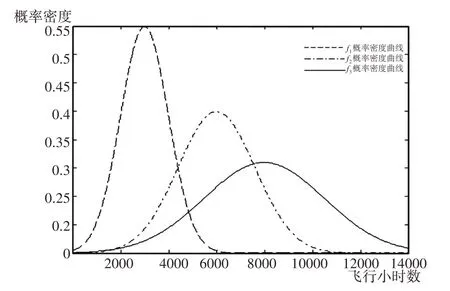
圖3 發動機剩余清洗時間概率密度函數的預測Fig.3 Prediction of Remaining Engine Cleaning Time Probability Density Function

由剩余清洗時間概率密度函數積分可得發動機預測的剩余清洗時間，如表4所示。

表4 發動機清洗預測值與實際值對比Tab.4 Comparison Between Predicted Value and Actual Value of Engine Cleaning

5.2 模型驗證

某航空公司選擇40架同型飛機的80臺發動機，并將其他未選中的108架飛機作為對比組。采用新方法試運行一年，發動機清洗維修間隔可以偏離現有維修方案規定的1000發動機飛行小時，但最高不得超過1600飛行小時。兩種機隊試運行的數據情況，如圖4所示。該方法清洗發動機衰退速率較慢，即說明該方法較好。

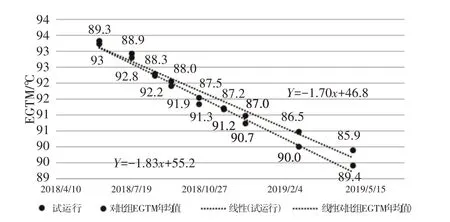
圖4 兩種清洗方法對比Fig.4 Comparison of Two Cleaning Methods

6 結論

根據某航空公司發動機清洗前后EGTM 數據，得到發動機的性能衰退模型，依據Rolls-Royce公司的節省燃油量模型，基于總成本最低的發動機清洗門閥值，可得首次發動機清洗門閥值（EGTM）為33.6℃。依據Wiener預測模型和貝葉斯更新理論，確定Wiener預測模型的參數，最后通過發動機剩余性能概率密度函數可得給定飛行小時的預測剩余清洗時間，最后分析某公司機隊運行數據，結果表明用新方法清洗的發動機性能衰退較慢，本方法較好。