高速旋轉鉸接式旋翼的固有特性分析

韓 偉，齊 龍，肖中云

（中國空氣動力研究與發展中心，四川 綿陽 621000）

1 引言

旋翼是直升機不可或缺的重要部件，其動力學特性對于直升機的動力穩定性和安全性具有不可忽視的影響，對于旋翼，一些看起來不重要的設計變化都可能導致動力學特性的顯著變化[1]。為了保證滿意的動力學特性，就必須在研制的過程中予以控制，而這些特性主要指其模態特性：固有頻率和振型等。

槳葉在實際振動中，三個自由度通常是耦合的，其傳統的固有振動特性計算方法主要包括：假設模特法、傳遞矩陣法和有限元法。最早使用的假設模態法是假設一組滿足相應邊界條件的函數序列，去逼近要求的模態函數，應用能量原理求得槳葉固有頻率和振型的方法，此法主要包括拉格朗日法、瑞利法和伽遼金法，這種方法很不方便，目前已經很少使用。文獻[2-3]基于傳遞矩陣法分析了旋翼的固有振動特性，雖然該法簡單方便，計算效率較高，但這種方法容易遺漏固有頻率，特別是當兩個固有頻率很接近時。文獻[4-5]基于有限元方法分析了旋翼的固有振動特性，但這種方法主要適用于單體問題。文獻[6]基于多體動力學程序建立了旋翼的結構動力學模型，文獻[7]基于多體動力學方法計算了鉸接式旋翼的固有頻率，但是這種基于都是基于變分原理的完全積分方法，存在不可避免的剪切自鎖現象，有限體積方法具有積分守恒的特點，能有效避免剪切自鎖現象[8-9]。目前少有文獻基于有限體積法對旋翼系統進行詳細的固有振動特性分析。

基于有限體積法結合多體動力學方法，編寫相關程序建立了旋翼的多體模型，其具有非線性負扭、后掃掠角并計及槳轂的扭轉剛度，首先計算了旋翼在工作轉速下的固有頻率和振型，對比分析表明有限體積法能夠對旋翼進行準確的模擬并展現此方法不存在剪切自鎖的現象；同時還研究了轉速、后掃掠結構和槳榖剛度對旋翼固有頻率的影響。

2 有限體積梁理論

2.1 控制方程

有限部分梁的兩端為點a和點b，梁上任意一個截面的內力?為：

式中：F、M—梁截面的內力和內力矩；?a、?b—兩端所受到的內力和內力矩記；—端點a到端點b的梁域，在梁域上有如下的平衡公式：

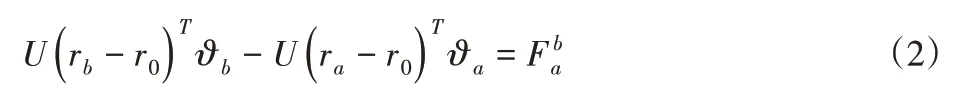
其中，力臂矩陣U定義如下式所示：

式中：ra、rb—梁的兩個端點的位置坐標向量，上式中利用支點代替梁截面的剪切中心來簡化計算平衡方程中的力矩項，r0是支點的位置坐標向量，支點一般取梁的兩個端點。外部力定義如下：

其中，τ是廣義上的外力和外力矩，其包含外部荷載τout和慣性力τin兩部分，其中慣性力可表示如下：

式中：M—梁的慣性矩陣；r?—線加速度；ω?—角加速度。

2.2 數值方法

槳葉模型采用幾何精確梁模型［10］，此模型為三維模型，對于梁的狀態用四個變量（軸向變形u、擺振變形v、揮舞變形w和描述截面轉動變形量的Gibbs-Rodriguez參數）描述。

采用三節點有限體積梁單元對梁模型進行離散，如圖1 所示。每個三節點梁單元有兩個控制中心節點Ⅰ和Ⅱ，中心節點采用2個高斯積分點使得多項式的積分達到了三階精度，每個三節點有限體積梁單元中心節點具有四個變量（軸向變形u、擺振變形v、揮舞變形w和截面轉動Gibbs-Rodriguez 參數g），有限體積梁模型的兩個控制中心節點位于參考系的坐標和sII=，控制體中心節點之間的邊界面可以通過兩個中心節點的變量插值得到。

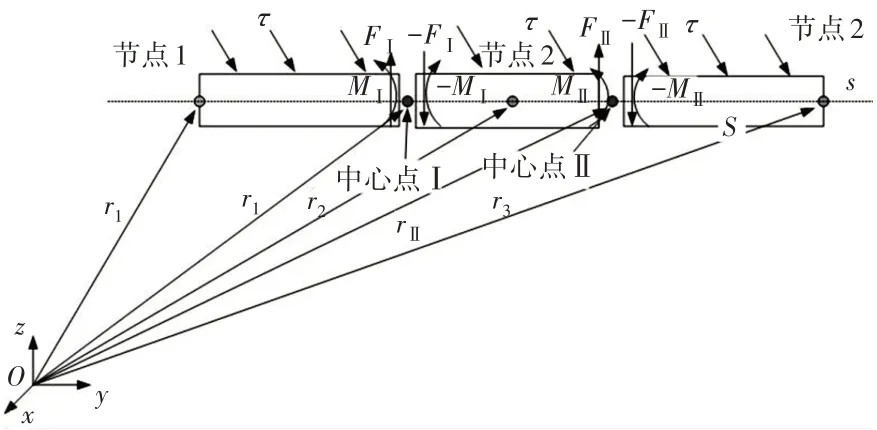
圖1 三節點有限體積梁單元受內力和外力示意圖Fig.1 The Three-Node Finite Volume Beam Element Under Internal and External Loads

存在如下所示的二次多項式組合函數(Nj(s))：

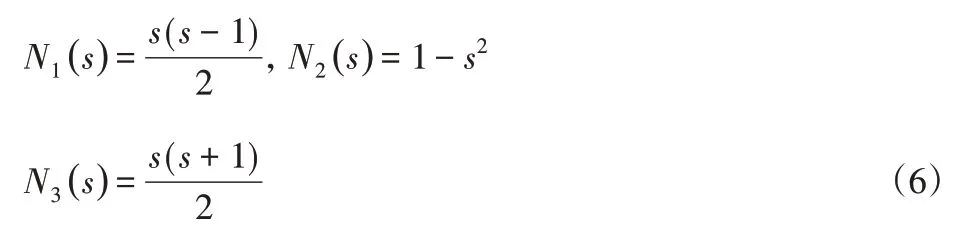
于是，梁單元上的任意一點的位置r(s)和方向參數g(s)都可以表示為節點1、2、3相應參數的線性組合。參考線上任意一點的位置為：

式中：Nj—第j個節點的形函數；rj—第j個節點的位置向量，上式表示的是以j為指針的求和運算，其中j=1，2，3。同理，任意一點的方向參數可表示為：

式中：gj—第j個節點的方向參數，當s=-1，0，1分別對應的是3個節點在局部坐標系中的位置。

離散后，三節點有限體積梁單元受力，如圖1所示。該單元的離散方程包含三段梁的平衡方程，其公式如下所示：

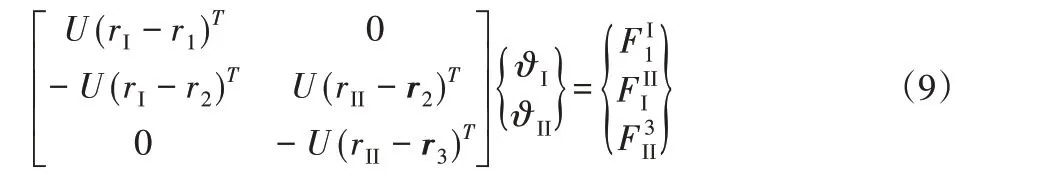
式中：U—力臂矩陣；?I、?II—兩個中心節點Ⅰ和Ⅱ的內力和內力矩；F—廣義上的外力項。

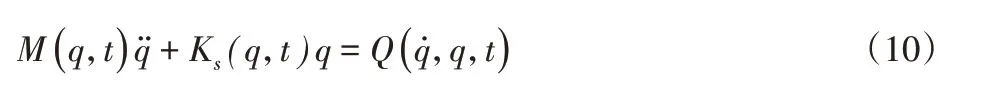
列出所有離散單元的平衡方程，并進行方程組裝，可得到一般矩陣形式的方程，其壓縮形式如下：式中：M(q，t)—整體的質量矩陣；Ks(q，t)—結構剛度矩陣；自由度向量；—空氣動力或者其它的外部力以及慣性力。

2.3 固有頻率提取

對于上述的振動方程，去掉外力項，即τout=0，其動力學變為如下的一般形式：

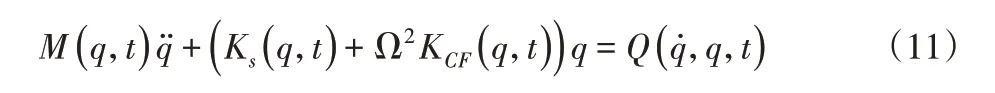
上式還可以進一步寫成如下的簡化形式：

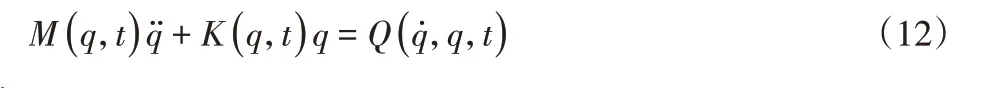
式中：K(q，t)=Ks(q，t)+Ω2KCF(q，t)，由梁的理論可假設位移響應滿足如下關系：

將式（12）寫成如下矩陣形式：

式中：ωn—系統的固有頻率，ωn對應的解qn是系統的振型向量。考慮相應的邊界條件以后，考慮相關位移約束方程后，求解上述頻率方程，即可得到系統的固有頻率和振型。例如對于固定約束，該處線位移和角位移均為0，而自由端的彎矩和剪力都為0。

3 旋翼的有限體積多體模型

基于有限體積C0梁單元建立了現代先進直升機UH-60A旋翼的多體模型，該旋翼具有許多先進直升機旋翼的幾何特征，如非線性負扭轉、后掠和不同的翼型組合等，槳葉的非線性扭轉角分布，如圖2所示。文獻［7，11］給出了較為詳細的結構和材料參數。該旋翼由四片槳葉組成，槳葉的展弦比15.3，后掠位置位于槳葉的93%R 處，后掠角為20°。槳葉由兩種翼型構成，兩段為SC1095翼型，中間部分為SC1095-R8翼型。槳葉的具體原始數據，如表1所示。

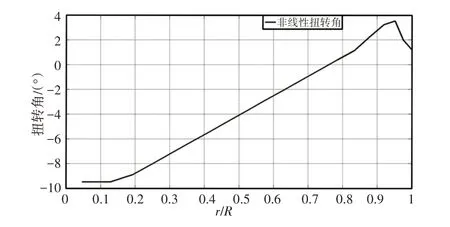
圖2 UH-60A槳葉的扭轉角分布Fig.2 The Torsion Angle Distribution of UH-60A Blade

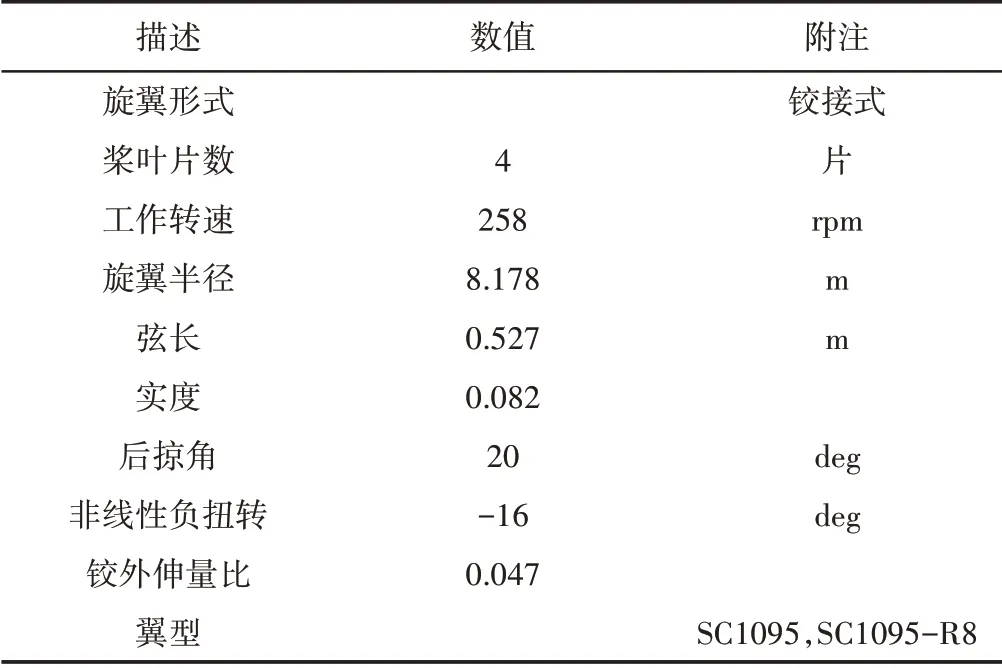
表1 UH-60A旋翼的相關參數Tab.1 The Correlation Parameter of UH-60A Blade

槳葉模型采用三節點有限體積梁單元建模，一共才采用了23個梁單元，直梁部分具有19個梁單元，后掃掠結構具有4個梁單元，槳轂采用孤立的剛性節點模擬，如圖3所示。支撐點采用固定約束，旋翼根部采用變距鉸、揮舞鉸和擺振鉸約束，并在變距、揮舞和擺振方向上施加變形彈簧。為了考慮旋翼的變距系統的剛度對其固有頻率的影響，將其等效為一常數剛度值，施加在旋翼根部的變距鉸上，剛度值K0=84708N·m/rad[12]。槳葉的慣性通過集中質量單元來考慮，集中質量單元附加在梁單元的節點上。旋翼槳葉的后掃掠結構，采用真實拓撲建立模型，考慮其幾何拓撲結構對其固有特性的影響。該模型為這里的第Ⅰ種模型。

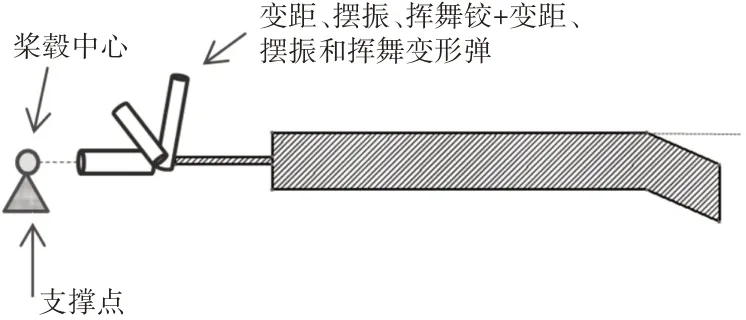
圖3 UH-60A旋翼的有限體積梁模型Fig.3 Finite Volume Beam Model of UH-60A

共建立三種不同的旋翼模型，以詳細分析不同的邊界條件、模型參數和拓撲結構對旋翼固有特性的影響，第Ⅱ種旋翼模型，除槳葉無后掃掠結構外，與模型Ⅰ完全相同。其中第Ⅲ種旋翼模型的槳葉根部采用擺振鉸、揮舞鉸，無扭轉彈簧，即槳葉根部節點的扭轉變形為零，其扭轉自由度被完全鎖死，如表2所示。

表2 三種模型的對比Tab2. The Comparison of Three Modals

4 計算結果與分析

在上述有限體積多體模型的基礎上，基于非對稱特征值QZ分解法計算了UH-60A旋翼在總距角為14.5°、工作轉速狀態下的扭轉、揮舞和擺振的前幾階固有頻率。這里的頻率計算結果與參考值的對比[7]，如表3所示。表中的頻率值按工作轉速無量綱化，并給出了相應模態的固有振型。

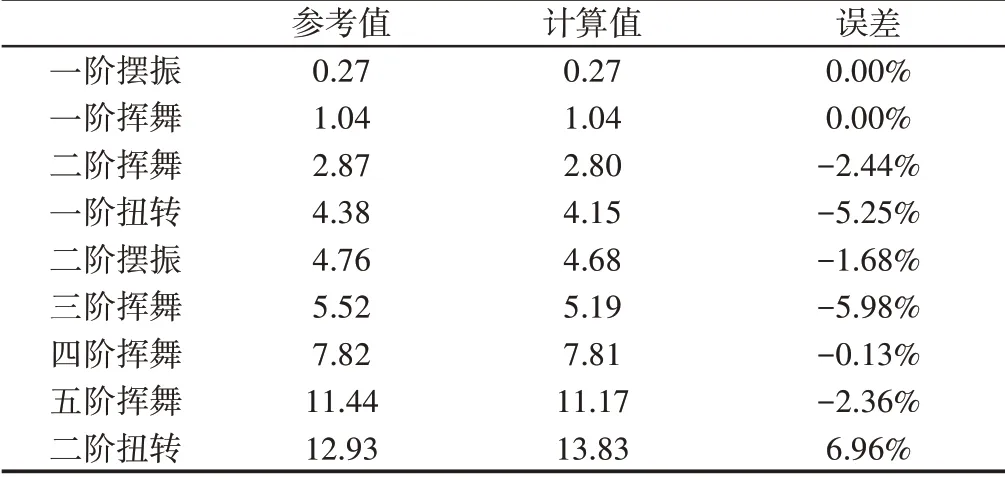
表3 計算結果與參考值的對比Tab.3 The Comparison of Computation Values and Reference Values

由上表可知，計算的頻率值與參考值的誤差均在工程計算誤差要求范圍以內，最大誤差不超過7%，由此驗證了這里的模型是可靠的。需要說明的是文獻[7]以直梁模型對槳葉模型進行了等效化處理，也導致了這里計算值與參考值存在一定的差別。

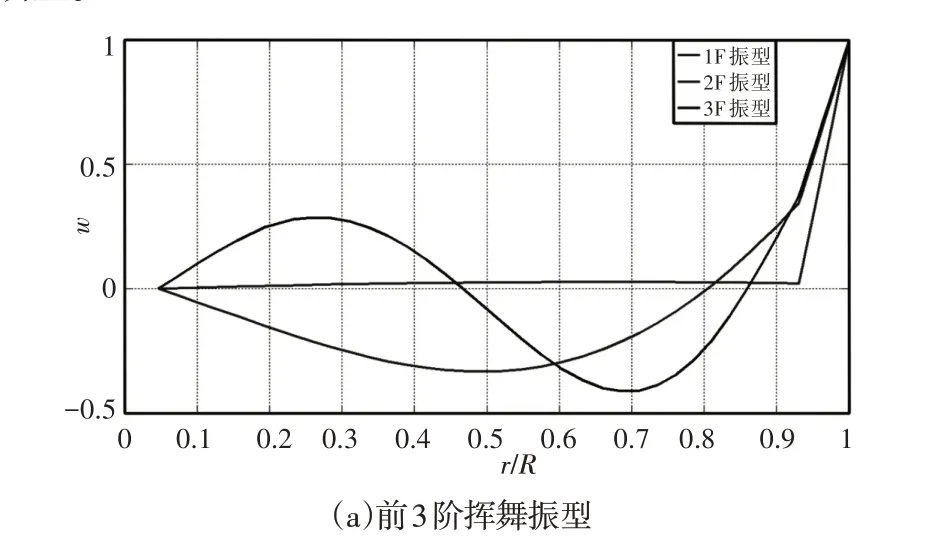
計算所得的各階模態對應的前五階揮舞、前兩階擺振和前兩階扭轉振型，如圖4所示。由圖可見，鉸接式帶后掃掠角的旋翼的一階揮舞和一階擺振振型呈直線式分布，由于該旋翼考慮了旋翼根部傾轉系統的扭轉剛度對其固有特性的影響，其扭轉振型在根部的值具有一定的大小，其它各階的計算結果也分別符合鉸接式旋翼的分布規律。圖標F、L、T分別表示揮舞、擺振和扭轉模態。

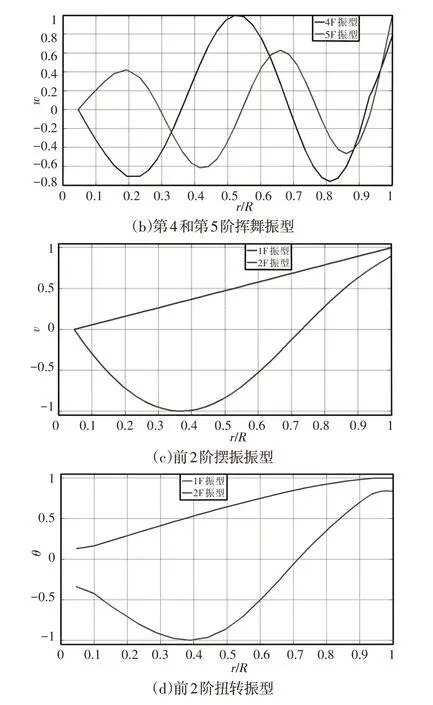
圖4 UH-60A旋翼的模態振型Fig.4 The Mode Shapes of UH-60A

計算了旋翼在（0～2）倍工作轉速時的固有頻率，以研究轉速對旋翼固有頻率的影響，計算結果，如圖5所示。圖中轉速采用無量綱轉速表示。由圖可知，轉速對旋翼的固有頻率具有明顯的“剛化效應”，各階頻率隨著轉速的增大而增大，其對揮舞和擺振頻率的剛化效應比較明顯，而對扭轉頻率的剛化效應不是很明顯。

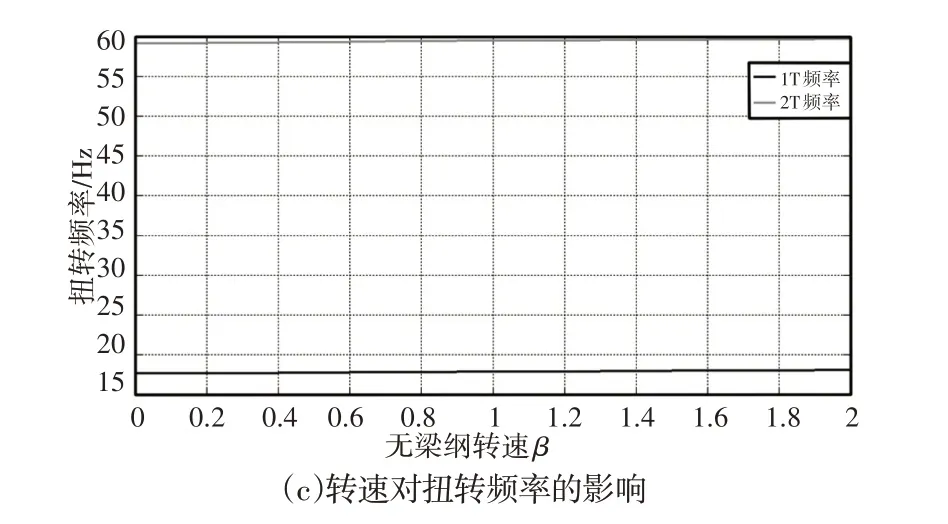
圖5 轉速對旋翼頻率的影響Fig.5 The Effect of Rotor Speed on Rotor Frequency

為了進一步分析邊界條件對旋翼固有頻率的影響，對模型Ⅲ進行了固有特性計算，并與模型Ⅰ進行了對比分析，如表4所示。由表可知，當槳葉根部的扭轉剛度很大時，采用兩種模型計算結果很接近，當槳葉根部的扭轉剛度不是特別大時，就必須考慮旋翼變距系統的扭轉剛度對槳葉固有頻率的影響。

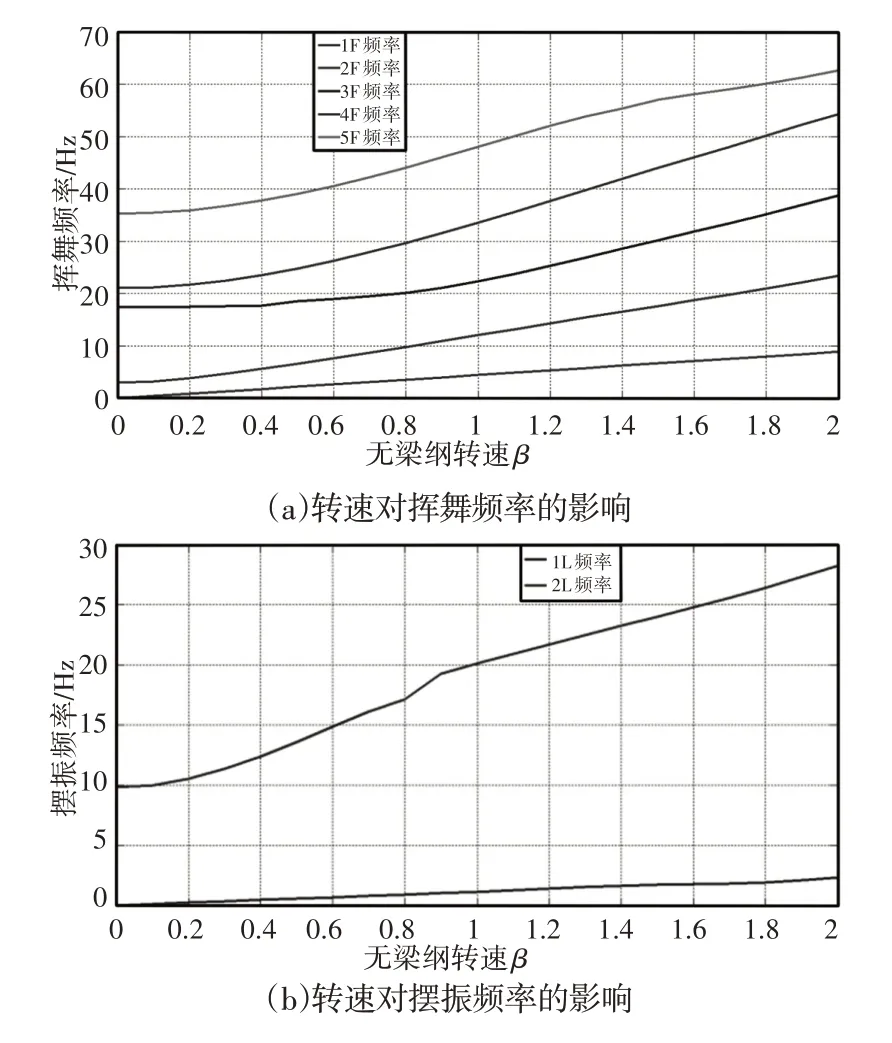
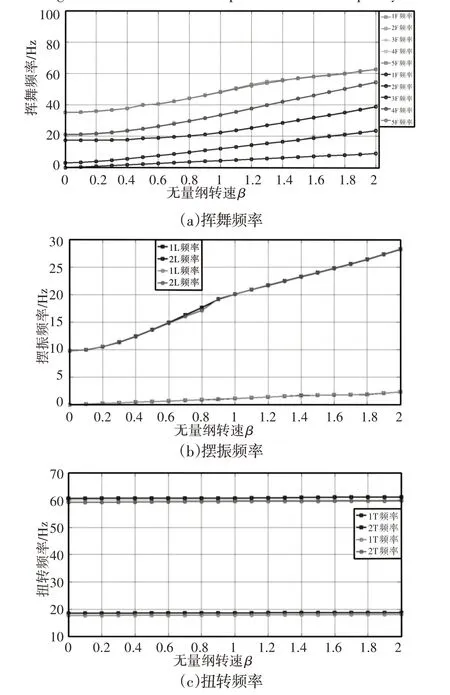
圖6 后掃掠結構對旋翼頻率的影響Fig.6 The Effect of Back Swept Structure on the Frequency of Blade

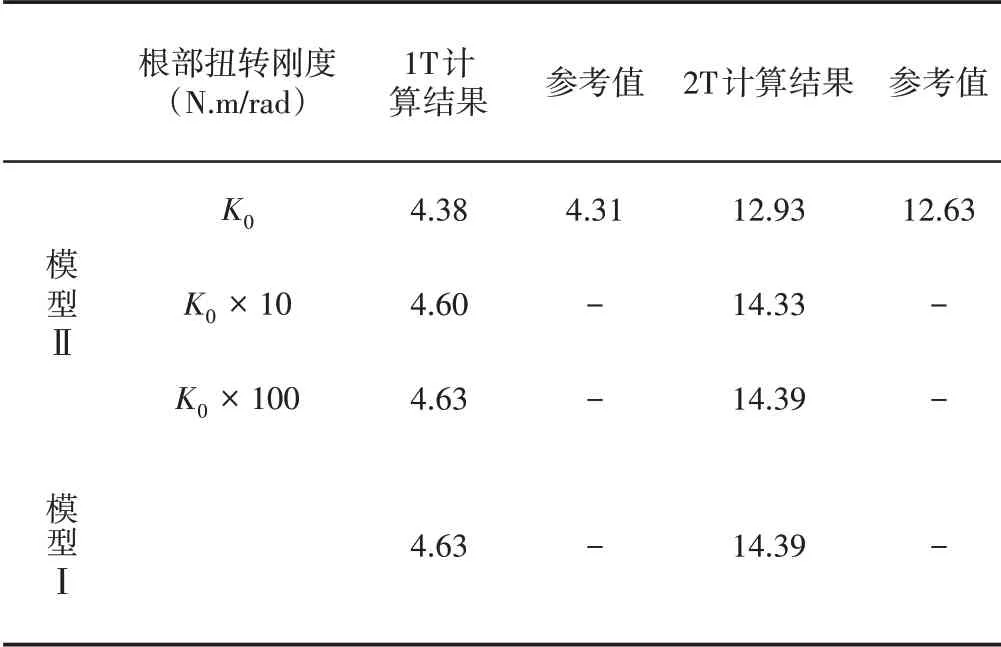
表4 模型Ⅰ和模型Ⅱ的扭轉頻率計算結果的對比Tab.4 The Comparison of Torsion Frequency of ModalⅠand ModalⅡ

對于帶槳轂彈簧的鉸接式旋翼，槳葉的根部受到彈簧的彈性約束。當槳葉根部的擺振剛度K2=0～212×103N·m/rad時，頻率計算結果如所示，橫坐標為2的指數值。由圖7（b）可知，與扭轉頻率的變化規律類似，前二階擺振頻率隨著擺振剛度的增加而較快增加，且增加的幅度越來越小，最后趨于水平。當槳葉根部的揮舞剛度K3=0～212×103N·m/rad時，其頻率計算結果，如圖7（c）所示。橫坐標為2的指數值。由圖可知，揮舞頻率的變化規律與扭轉和擺振頻率類似，前五階揮舞頻率隨著根部揮舞剛度的增加而較快增加，且增加的幅度越來越慢，最后趨于水平。

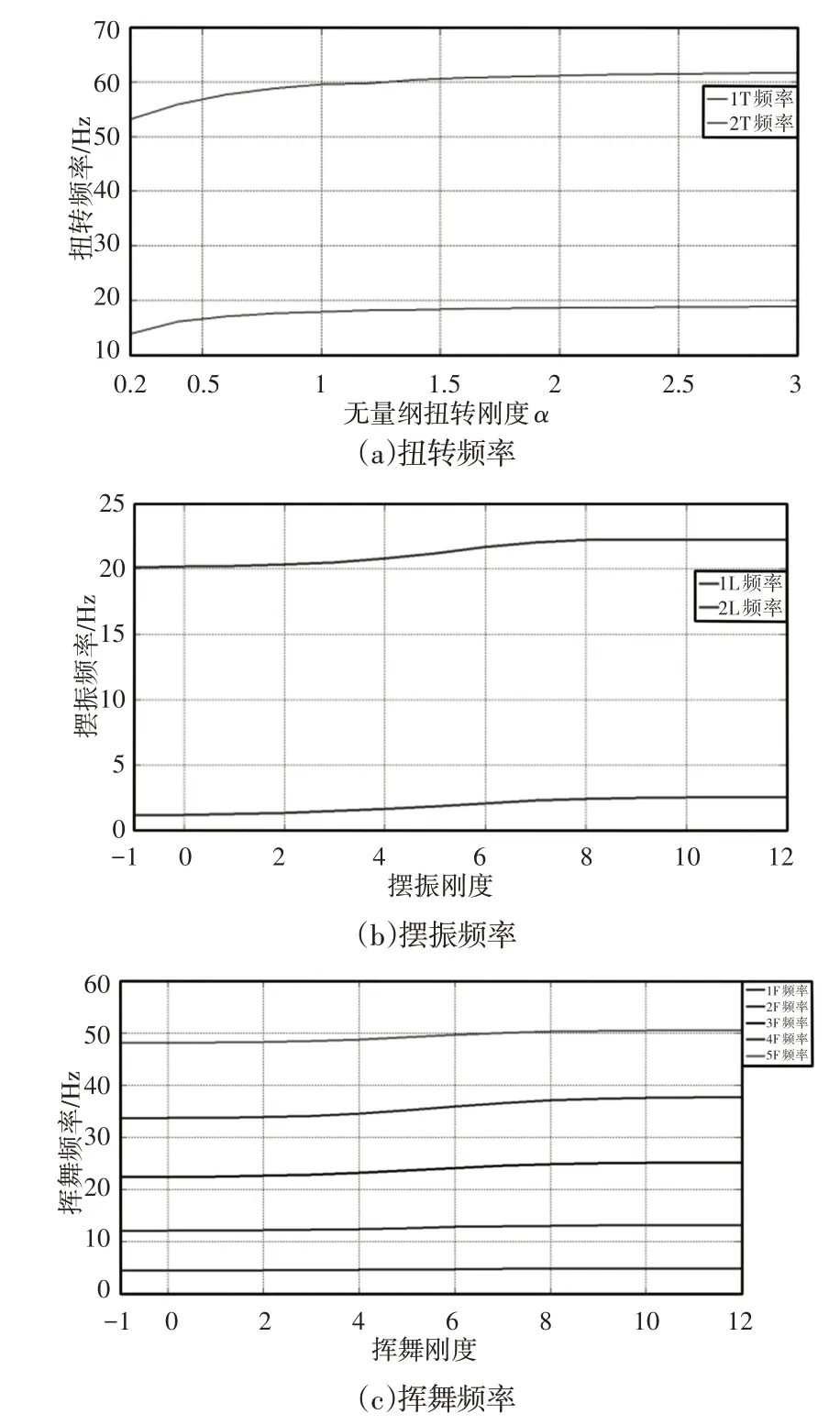
圖7 扭轉、擺振和揮舞剛度對旋翼固有頻率的影響Fig.7 The Effect of Torsion and Level and Flap Stiffness on Frequency of Blade

5 結論

基于有限體積法，采用有限體積梁單元建立了旋翼的多體模型，基于非對稱特征值QZ分解法計算了高速旋轉運動條件下該旋翼的固有頻率和振型，并分別分析了轉速、后掃掠結構和槳葉根部約束剛度對其固有特性的影響。得出以下結論：

（1）基于有限體積方法能夠準確計算旋翼的固有頻率和振型，并可方便地計及槳葉根部變距系統的扭轉剛度，誤差在可接受范圍之內；

（2）轉速對旋翼的固有頻率具有明顯的剛化效應，尤其是對擺振和揮舞頻率的剛化效應大，而對扭轉頻率的剛化效應小；

（3）槳葉的后掃掠結構對其擺振、揮舞頻率影響很小，而后掃掠結構降低了槳葉的扭轉頻率，在旋翼的設計中應該適當加以考慮；

（4）槳葉根部的扭轉、擺振和揮舞剛度分別對其扭轉、擺振和揮舞振型的頻率都有較大的影響，在計算其固有特性時，應根據實際結構適當加以考慮，不宜一概完全忽略不計，以免降低計算精度。